Abstract
In extant quantum secret sharing protocols, once the secret is shared in a quantum network (qnet) it cannot be retrieved, even if the dealer wishes that his/her secret no longer be available in the network. For instance, if the dealer is part of the two qnets, say \({\mathcal {Q}}_1\) and \({\mathcal {Q}}_2\) and he/she subsequently finds that \({\mathcal {Q}}_2\) is more reliable than \({\mathcal {Q}}_1\), he/she may wish to transfer all her secrets from \({\mathcal {Q}}_1\) to \({\mathcal {Q}}_2\). Known protocols are inadequate to address such a revocation. In this work we address this problem by designing a protocol that enables the source/dealer to bring back the information shared in the network, if desired. Unlike classical revocation, the no-cloning theorem automatically ensures that the secret is no longer shared in the network. The implications of our results are multi-fold. One interesting implication of our technique is the possibility of routing qubits in asynchronous qnets. By asynchrony we mean that the requisite data/resources are intermittently available (but not necessarily simultaneously) in the qnet. For example, we show that a source S can send quantum information to a destination R even though (a) S and R share no quantum resource, (b) R’s identity is unknown to S at the time of sending the message, but is subsequently decided, (c) S herself can be R at a later date and/or in a different location to bequeath her information (‘backed-up’ in the qnet) and (d) importantly, the path chosen for routing the secret may hit a dead end due to resource constraints, congestion, etc., (therefore the information needs to be back-tracked and sent along an alternate path). Another implication of our technique is the possibility of using insecure resources. For instance, if the quantum memory within an organization is insufficient, it may safely store (using our protocol) its private information with a neighboring organization without (a) revealing critical data to the host and (b) losing control over retrieving the data. Putting the two implications together, namely routing and secure storage, it is possible to envision applications like quantum mail (qmail) as an outsourced service.



Similar content being viewed by others
References
Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935)
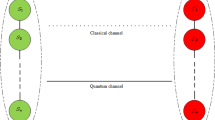
Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)
Bouwmeester, D., Pan, J.-W., Mattle, K., Eibl, M., Weinfurter, H., Zeilinger, A.: Experimental quantum teleportation. Nature 390, 575–579 (1997)
Gisin, N., Ribordy, G., Tittel, W., Zbinden, H.: Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002)
Hillery, M., Buzek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999)
Cleve, R., Gottesman, D., Lo, H.-K.: How to share a quantum secret. Phys. Rev. Lett. 83, 648–651 (1999)
Karlsson, A., Koashi, M., Imoto, N.: Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 59, 162–168 (1999)
Bandyopadhyay, S.: Teleportation and secret sharing with pure entangled states. Phys. Rev. A 62, 012308 (2000)
Bagherinezhad, S., Karimipour, V.: Quantum secret sharing based on reusable Greenberger-Horne-Zeilinger states as secure carriers. Phys. Rev. A 67, 044302 (2003)
Lance, A.M., Symul, T., Bowen, W.P., Sanders, B.C., Lam, P.K.: Tripartite quantum state sharing. Phys. Rev. Lett. 92, 177903 (2004)
Gordon, G., Rigolin, G.: Generalized quantum-state sharing. Phys. Rev. A 73, 062316 (2006)
Zheng, S.B.: Splitting quantum information via W states. Phys. Rev. A 74, 054303 (2006)
Keet, A., Fortescue, B., Markham, D., Sanders, B.C.: Quantum secret sharing with qudit graph states. Phys. Rev. A 82, 062315 (2010)
Markham, D., Sanders, B.C.: Graph states for quantum secret sharing. Phys. Rev. A 78, 042309 (2008)
Li, Q., Chan, W.H., Long, D.-Y.: Semiquantum secret sharing using entangled states. Phys. Rev. A 82, 022303 (2010)
Adhikari, S.: Quantum secret sharing with two qubit bipartite mixed states. arXiv:1011.2868
Adhikari, S., Chakrabarty, I., Agrawal, P.: Probabilistic secret sharing through noise quantum channel. Quantum Inf. Comput. 12, 0253–0261 (2012)
Tittel, W., Zbinden, H., Gisin, N.: Experimental demonstration of quantum secret sharing. Phys. Rev. A 63, 042301 (2001)
Schmid, C., Trojek, P., Bourennane, M., Kurtsiefer, C., Zukowski, M., Weinfurter, H.: Experimental single qubit quantum secret sharing. Phys. Rev. Lett. 95, 230505 (2005)
Schmid, C., Trojek, P., Gaertner, S., Bourennane, M., Kurtsiefer, C., Zukowski, M., Weinfurter, H.: Experimental quantum secret sharing. Fortschritte der Physik 54, 831–839 (2006)
Bogdanski, J., Rafiei, N., Bourennane, M.: Experimental quantum secret sharing using telecommunication fiber. Phys. Rev. A 78, 062307 (2008)
Sazim, S., Chakrabarty, I.: A study of teleportation and super dense coding capacity in remote entanglement distribution. Eur. Phys. J. D 67(8), 174 (2013)
Paparo, G.D., Martin-Delgado, M.A.: Google in a quantum network. Nat. Sci. Rep. 2, 444 (2012). arXiv:1112.2079
Paparo, G.D., Mueller, M., Comellas, F., Martin-Delgado, M.A.: Quantum Google in a complex network. Sci. Rep. 3, 2773 (2013)
Lemr, K., Bartkiewicz, K., Cernoch, A., Soubusta, J.: Resource-efficient linear-optical quantum router. Phys. Rev. A 87, 062333 (2013)
Lemr, K., Cernoch, A.: Linear-optical programmable quantum router. Opt. Commun. 300, 282–285 (2013)
Qin, Su-Juan, Gao, Fei, Wen, Qiao-Yan, Zhu, Fu-Chen: Cryptanalysis of the Hillery-Buek-Berthiaume quantum secret-sharing protocol. Phys. Rev. A 76, 062324 (2007)
Wang, Tian-Yin, Wen, Qiao-Yan: Security of a kind of quantum secret sharing with single photons. Quantum Inf. Comput. 11(5–6), 0434–0443 (2011)
Wang, Tian-Yin, Li, Yan-Ping: Cryptanalysis of dynamic quantum secret sharing. Quantum Inf. Process. 12(5), 1991–1997 (2013)
Acknowledgments
This work is done at Center for Security, Theory and Algorithmic Research (CSTAR), IIIT, Hyderabad, and S Sazim gratefully acknowledge their hospitality. We acknowledge Prof. P. Agrawal for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
Consider a 3-qubit GHZ state \(\frac{1}{\sqrt{2}}\{|000\rangle +|111\rangle \}\) among Alice, Bob and Charlie and let \(|\psi \rangle = \alpha |0\rangle +\beta |1\rangle \) be the message with Alice.
Appendix 2
Suppose Alice and Bob share a bell state \(\frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{AB}\) and the secret is already being shared between Bob and Charlie is \(\{\alpha |00\rangle +\beta |11\rangle \}_{BC}\).
Appendix 3
Suppose \(R_i\) is the authorized receiver sending request to Charlie and sharing a bell state \(\frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{CR_i}\) with charlie. Suppose \(\{\alpha |00\rangle +\beta |11\rangle \}_{BC}\) is shared among Bob and Charlie.
Appendix 4
Suppose \((A_1, B_1)\) has the shared secret \(\{\alpha |00\rangle +\beta |11\rangle \}_{A_{1s}B_{1s}}\) as a result of bell measurement at the sender (S). Assume the pairs \((A_1, A_2), (B_1, B_2)\) and \((B_2, R)\) share Bell states \(\frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{A_{1r}A_{2r}}, \frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{B_{1r}B_{2r}}\) and \(\frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{B_{2r}R}\), respectively. The following is a sequence of measurements that transfers the secret in shared form from \((A_1, A_2)\) to \((B_1, B_2)\) so that R can be able to reconstruct it.
-
1.
Bell Measurement at \(A_1\) on qubits \(A_{1s}\) and \(A_{1r}\).
$$\begin{aligned}&\{\alpha |00\rangle +\beta |11\rangle \}_{A_{1s}B_{1s}}\otimes \frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{A_{1r}A_{2r}} {}\nonumber \\&=\frac{1}{\sqrt{2}}\{\alpha |00\rangle |00\rangle + \alpha |01\rangle |01\rangle +\beta |10\rangle |10\rangle +\beta |11\rangle |11\rangle \}_{A_{1s}A_{1r}B_{1s}A_{2r}} {}\nonumber \\&= \frac{1}{2}\{\alpha [|\phi ^+\rangle + |\phi ^-\rangle ]|00\rangle +\alpha [|\psi ^+\rangle + |\psi ^-\rangle ]|01\rangle +\beta [|\psi ^+\rangle \nonumber \\&\quad -\, |\psi ^-\rangle ]|10\rangle +\beta [|\phi ^+\rangle - |\phi ^-\rangle ]|11\rangle \}_{A_{1s}A_{1r}B_{1s}A_{2r}} {}\nonumber \\&= \frac{1}{2}\{|\phi ^+\rangle [\alpha |00\rangle +\beta |11\rangle ] + |\phi ^-\rangle [\alpha |00\rangle -\beta |11\rangle ]+|\psi ^+\rangle [\alpha |01\rangle +\beta |10\rangle ]\nonumber \\&\quad +\,|\psi ^-\rangle [\alpha |01\rangle -\beta |10\rangle ]\}_{A_{1s}A_{1r}B_{1s}A_{2r}} \end{aligned}$$(4)Suppose \(|\psi ^+\rangle \) is the outcome of this measurement, the new state of the secret will be \(\{\alpha |01\rangle +\beta |10\rangle \}_{B_{1s}A_{2s}}\) with \((B_1,A_2)\). This outcome will be sent to S classically to keep track of the present state of the secret.
-
2.
Bell Measurement at \(B_1\) on qubits \(B_{1s}\) and \(B_{1r}\).
$$\begin{aligned}&\{\alpha |01\rangle +\beta |10\rangle \}_{B_{1s}A_{2s}}\otimes \frac{1}{\sqrt{2}}\{|00\rangle +|11\rangle \}_{B_{1r}B_{2r}} {}\nonumber \\&=\frac{1}{\sqrt{2}}\{\alpha |00\rangle |10\rangle + \alpha |01\rangle |11\rangle +\beta |10\rangle |00\rangle +\beta |11\rangle |01\rangle \}_{B_{1s}B_{1r}A_{2s}B_{2r}} {}\nonumber \\&= \frac{1}{2}\{\alpha [|\phi ^+\rangle + |\phi ^-\rangle ]|10\rangle +\alpha [|\psi ^+\rangle + |\psi ^-\rangle ]|11\rangle +\beta [|\psi ^+\rangle - |\psi ^-\rangle ]|00\rangle +\beta [|\phi ^+\rangle \nonumber \\&\quad - |\phi ^-\rangle ]|01\rangle \}_{B_{1s}B_{1r}A_{2s}B_{2r}} {}\nonumber \\&= \frac{1}{2}\{|\phi ^+\rangle [\alpha |10\rangle +\beta |01\rangle ] +|\phi ^-\rangle [\alpha |10\rangle -\beta |01\rangle ]+|\psi ^+\rangle [\alpha |11\rangle +\beta |00\rangle ]\nonumber \\&\quad +\,|\psi ^-\rangle [\alpha |11\rangle -\beta |00 \rangle ]\}_{B_{1s}B_{1r}A_{2s}B_{2r}} \end{aligned}$$(5)Suppose \(|\phi ^-\rangle \) is the outcome of this measurement, the new state of the secret will be \(\{\alpha |10\rangle -\beta |01\rangle \}_{A_{2s}B_{2s}}\) with \((A_2,B_2)\). This outcome will be sent to S classically to keep track of the present state of the secret.
Rights and permissions
About this article
Cite this article
Sazim, S., Chiranjeevi, V., Chakrabarty, I. et al. Retrieving and routing quantum information in a quantum network. Quantum Inf Process 14, 4651–4664 (2015). https://doi.org/10.1007/s11128-015-1109-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-015-1109-7