Imposing regional monotonicity on translog stochastic production frontiers with a simple three-step procedure

Abstract

We show that the monotonicity condition is conceptually important in Stochastic Frontier Analysis (SFA). Despite its importance, most empirical studies do not impose monotonicity—probably because existing approaches are rather complex and laborious. Therefore, we propose a three-step procedure that is much simpler than existing approaches. We demonstrate how monotonicity of a translog function can be imposed regionally at a connected set (region) of input quantities. Our method can be applied not only to impose monotonicity on translog production frontiers but also to impose other restrictions on cost, distance, or profit frontiers.

1 Introduction

The analysis of technical efficiency is a widely used tool in empirical production studies. It is generally based on a “frontier” production function that represents the maximum output quantities attainable from each set of input quantities (Coelli et al. 2005). This methodology accounts for the fact that not all producers succeed in optimizing their production processes and might not achieve the maximum output level given their input quantities. It is often used to explore and compare the (relative) efficiencies of different producers and to determine factors that influence the producer’s efficiency.

Microeconomic theory implies that production functions should monotonically increase in all inputs. The importance of theoretical consistency in frontier analysis has been already stressed by Sauer et al. (2006). We show that the monotonicity property is particularly important for estimating the (relative) efficiencies of individual firms because otherwise a reasonable interpretation of the results is impossible (see also O’Donnell and Coelli 2005). The non-parametric non-stochastic Data Envelopment Analysis (DEA) implicitly imposes monotonicity while the parametric Stochastic Frontier Analysis (SFA) with flexible functional forms generally disregards this condition. Many empirical applications of SFA present results in which the monotonicity condition is not fulfilled, despite its importance (Sauer et al. 2006). Although procedures for imposing monotonicity of frontier functions have been proposed in the literature, they are rarely used ¹—probably because these procedures are rather complex and laborious. Therefore, we present a new three-step procedure that is much simpler and can be used also by practitioners. Furthermore, we demonstrate how monotonicity of a translog function can be imposed not only locally at a single data point but regionally at a connected set (region) of data points.

2 Theoretical consistency of production frontiers

2.1 Monotonicity

As noted above, microeconomic theory requires that production functions monotonically increase in all inputs, i.e. the output quantity must not decrease if any input quantity is increased. The rationale for the monotonicity assumption is as follows: if (in rare cases) there is indeed a negative technical input–output relationship (e.g. too much fertilizer burns the crops), a wise manager would simply leave a part of the input unused (e.g. leave some of the fertilizer in the bag). Therefore, increasing the (unused) quantity of this input would leave the output (at least) unchanged.

Given the production function

$$ y = f ( \user2{x}, \varvec{\beta} ), $$

(1)

where y is the output quantity, $\user2{x}$ is a vector of n input quantities, and $\varvec{\beta}$ is a vector of parameters, monotonicity requires that all marginal products (f _i ) are positive

$$ f_i ( \user2{x}, \varvec{\beta} ) = \frac{\partial f( \user2{x}, \varvec{\beta} )} {\partial x_i} \geq 0 \; \forall \; i $$

(2)

If a production frontier is not monotonically increasing, the efficiency estimates of the individual firms cannot be reasonably interpreted. We illustrate this problem in Fig. 1. In this example, we have a non-monotone production frontier. Firm A is below the production frontier and hence, considered to be inefficient, while firm B is on the production frontier and hence, considered to be efficient. However, firm B uses much more of the input to produce the same output as firm A, which means that firm B uses its input less efficiently than firm A. Thus, the efficiency measures based on this non-monotone production frontier imply just the opposite of the actual situation and hence, the (relative) efficiency estimates based on a non-monotone production frontier cannot be reasonably interpreted.

Fig. 1

Non-monotone production frontier

We stress that it is not sufficient to ensure that the marginal products at all data points are non-negative. The same problem as demonstrated in Fig. 1 might occur if there are some non-monotone intervals between the data points. This is demonstrated in Fig. 2, in which the production frontier increases in the input quantity at both data points but decreases in the input quantity in an interval between the two data points.

Fig. 2

Production frontier with non-monotone interval

The problem of a non-monotone production frontier inhibits not only a reasonable interpretation of the individual (relative) efficiency estimates, but also the analysis of factors that might affect technical (in)efficiency. This is because the non-monotonicity distorts the efficiency estimates, which are the endogenous values in this analysis (e.g. in the “Technical Efficiency Effects Model” proposed by Battese and Coelli 1995).

If an estimated production frontier is not monotonically increasing in all inputs, the question of what to do arises. If the monotonicity condition is violated at many data points, the model is likely misspecified and we suggest changing the model specification. If the monotonicity condition is violated only at a few data points, these are probably random deviations from the “true” monotonically increasing production frontier and we suggest imposing the monotonicity condition in the estimation.

2.2 Quasiconcavity

Besides monotonicity, microeconomic theory often assumes that production functions are also quasiconcave in all inputs Lau (1978), because this implies convex input sets and hence, decreasing marginal rates of technical substitution. However, quasiconcave production functions do not guarantee that the input demand functions are “everywhere” differentiable (Dhrymes 1967; Barten et al. 1969).²

If all inputs are perfectly divisible and different production activities can be applied independently, production functions are generally quasiconcave (e.g. Varian 1992). Furthermore, a non-quasiconcave point of the production function cannot reflect profit-maximizing behavior under standard microeconomic assumptions. However, the assumptions of perfectly divisible inputs and independent applicability of different production activities are not always fulfilled in the real world and measuring technical efficiency generally assumes only that producers maximize output given their input quantities but not that producers maximize their profit. Hence, in contrast to the monotonicity assumption, there is not necessarily a technical rationale for production functions to be quasiconcave. Moreover, even a non-quasiconcave point of the production function might reflect profit-maximizing behavior if not all of the prices are exogenously given or there are restrictions on input use (e.g. fertilizer use in water protection areas).

Hence, we suggest abstaining from imposing quasiconcavity when estimating (frontier) production functions. However, we propose to check for quasiconcavity after the econometric estimation because some standard results of microeconomic theory (e.g. convex input sets) do not hold in case of non-quasiconcavity.

A function is quasiconcave if

$$ f ( \lambda \user2{x}^{\prime} + ( 1 - \lambda ) \user2{x}^{\prime\prime}, \varvec{\beta} ) \geq \min \left( f ( \user2{x}^{\prime}, \varvec{\beta} ), f ( \user2{x}^{\prime\prime}, \varvec{\beta} ) \right) $$

(3)

$$ \hbox {with } 0 < \lambda < 1. $$

(4)

In the case of a twice continuously differentiable production function f, quasiconcavity can be checked using its bordered Hessian matrix

$$ B = \left[ \begin{array} {lllll} 0 & f_1 & f_2 & \ldots & f_n \\ f_1 & f_{11} & f_{12} & \ldots & f_{1n} \\ f_2 & f_{21} & f_{22} & \ldots & f_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ f_n & f_{n1} & f_{n2} & \ldots & f_{nn} \\ \end{array}\right], $$

(5)

where $f_{ij} = \partial^2 f / ( \partial x_i \partial x_j )$ is the second derivative of the production function with respect to the ith and jth input quantity. Because all input quantities are generally non-negative ($x_i \geq 0 \forall i$), a necessary condition for quasiconcavity is

$$ |B_1| \leq 0, \; |B_2| \geq 0, \; |B_3| \leq 0, \ldots, |B_n| \cdot (-1)^n \geq 0, $$

(6)

where

$$ |B_1| = \left| \begin{array} {ll} 0 & f_1 \\ f_1 & f_{11} \\ \end{array} \right|, \quad |B_2| = \left| \begin{array} {llll} 0 & f_1 & f_2 \\ f_1 & f_{11} & f_{12} \\ f_2 & f_{21} & f_{22} \\ \end{array}\right|, \ldots, |B_n| = |B| $$

(7)

(Chiang 1984, p. 393f). If there is only one input (n = 1), monotonicity implies quasiconcavity (Takayama 1994, p. 62). In case of two or more inputs (n > 1), monotonicity does not (necessarily) imply quasiconcavity.

3 Restricted estimation of frontier functions

3.1 Approaches proposed in the literature

Despite the importance of monotonicity, our search of the literature found only a very few applications that impose this condition in SFA. One approach is a restricted maximum likelihood (ML) estimation, i.e. the likelihood function is maximized subject to the restriction that the theoretically derived properties of the frontier function are fulfilled. For instance, Bokusheva and Hockmann (2006) estimate a translog production frontier under monotonicity and quasi-concavity restrictions. However, they impose these restrictions only locally at the sample mean, which is not sufficient for obtaining reasonable efficiency estimates (see above). Furthermore, the maximization of the likelihood function under constraints is rather complex and the algorithms used for the optimization frequently have convergence problems or converge to local maxima.

As another solution, O’Donnell and Coelli (2005) use the Bayesian MCMC method to estimate a stochastic frontier distance function with all desirable theoretical conditions imposed at all data points. This is probably the most suitable and most sophisticated approach, but it is rather complex and laborious.

The main reason why the constrained ML and the MCMC approaches have been used so rarely is probably because these methods are not available in standard econometrics software packages. Hence, their application requires advanced skills in econometrics and in computer programming and many (applied) researchers and practitioners do not have the knowledge or the time to apply these methods.

3.2 Three-step procedure

As a solution, we propose a much simpler three-step procedure that is based on the two-step method suggested by Koebel et al. (2003).

In the first step, we estimate an unrestricted stochastic production frontier

$$ \ln y = \ln f( \user2{x}, \varvec{\beta} ) - u + v $$

(8)

$$ E[ u ] = \user2{z}^{\prime} \varvec{\delta}, $$

(9)

where u ≥ 0 captures technical inefficiency, v captures statistical noise, $\user2{z}$ is a vector of variables explaining technical inefficiency, and $\varvec{\delta}$ is a vector of parameters to be estimated. This estimation can be done by a standard software package for SFA. We extract the unrestricted parameters of the production frontier $\hat{\varvec{\beta}}$ and their covariance matrix $\hat{\varvec{\Upsigma}}_\beta$ from the estimation results.

In the second step, we obtain restricted $\varvec{\beta}$ parameters by a minimum distance estimation³:

$$ \hat{\varvec{\beta}}^0= \hbox{arg\,min} \left( \hat{\varvec{\beta}}^0 - \hat{\varvec{\beta}} \right) \hat{\varvec{\Upsigma}}_\beta^{-1} \left( \hat{\varvec{\beta}}^0 - \hat{\varvec{\beta}} \right) $$

(10)

$$ \hbox {s.t. } f_i ( \user2{x}, \hat{\varvec{\beta}}^0 ) \geq 0 \; \forall \; i, \user2{x} $$

(11)

This restricted minimization can be easily done by several software packages.⁴ The restricted parameters ($\hat{\varvec{\beta}}^0$) are asymptotically equivalent to a (successful) restricted one-step ML estimation (Koebel et al. 2003). However, it might be problematic to obtain a (consistent) covariance matrix of the restricted parameters $\hat{\varvec{\Upsigma}}_\beta^0$, because standard bootstrapping leads to an inconsistent covariance matrix if the restricted parameters are at the boundary of the feasible parameter space (Andrews 2000; Dhrymes 2006).⁵ Andrews (2000) suggests alternative methods, e.g. rescaled bootstrapping, that lead to a consistent covariance matrix even in the case of binding inequality constraints. However, these alternative methods are only valid under specific conditions that need to be checked for our specific case. Thus we leave this interesting topic for future research.⁶

In the third step, we determine the efficiency estimates of the firms and the effects of the variables explaining technical inefficiency based on the theoretical consistent production frontier. We estimate the stochastic frontier model

$$ \ln y =\alpha_0 + \alpha_1 \ln \tilde{y} - u^0 + v^0 $$

(12)

$$ E[ u^0 ] = \user2{z}^{\prime} \varvec{\delta}^0, $$

(13)

where the only “input variable” is the “frontier output” of each firm calculated with the parameters of the restricted model: $\tilde{y} = f( \user2{x}, \hat{\varvec{\beta}}^0 )$. Again, this estimation can be done with a standard software package for SFA. Parameters α₀ and α₁ allow an adjustment of the restricted production frontier, which gets

$$ y = e^{\alpha_0} f \left( \user2{x}, \hat{\varvec{\beta}}^0 \right)^{\alpha_1}. $$

(14)

As long as α₁ is positive, this adjustment is a strictly monotonically increasing transformation. Hence, it does not affect the monotonicity and quasiconcavity (Arrow and Enthoven 1961, p. 781) condition of $f( \user2{x}, \hat{\varvec{\beta}}^0 )$. However, if desired, an adjustment can be prevented by restricting α₀ to zero and α₁ to one.⁷ Since the estimation of Eq. 12 includes a generated regressor ($\tilde{y}$), the standard errors obtained in the third step might be biased (see Pagan 1984).

The monotonicity restrictions can be checked by statistical tests. In a first step, the inequality restrictions in (11) that are binding in the distance minimization (10) are determined. In a second step, standard statistical tests such as the Wald test or the likelihood ratio test are applied by treating the binding inequality restrictions as equality restrictions.

3.3 Translog production function

A popular functional form in SFA is the translog function. It satisfies second-order flexibility (Diewert 1974) and its logarithmic form has the advantage that inefficiencies are captured by an additive term rather than by a multiplicative term, which considerably simplifies the econometric estimation. A translog production function is defined as

$$ \ln y = \ln f( \user2{x}, \varvec{\beta} ) = \beta_0 + \sum_{i=1}^n \beta_i \ln x_i + \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \beta_{ij} \ln x_i \ln x_j $$

(15)

with β _ij = β _ji . Its marginal products are

$$ f_i =\frac{f( \user2{x}, \varvec{\beta} )}{x_i}\left( \beta_i + \sum_{j=1}^n \beta_{ij} \ln x_j \right) $$

(16)

and the second derivatives are

$$ f_{ij} = \frac{f( \user2{x}, \varvec{\beta} )}{x_i x_j} \left( \left( \beta_i + \sum_{k=1}^n \beta_{ik} \ln x_k \right) \left( \beta_j + \sum_{k=1}^n \beta_{jk} \ln x_k - \Updelta_{ij} \right) - \beta_{ij} \right), $$

(17)

where Δ _ij is Kronecker delta with Δ _ij = 1 if i = j and Δ _ij = 0 otherwise.

Because all input quantities must be non-negative and the translog functional form guarantees that the output quantity is always positive, the monotonicity conditions for the translog production function reduce to

$$ \beta_i + \sum_{j=1}^n \beta_{ij} \ln x_j \geq 0 \; \forall \; i. $$

(18)

Because these conditions are linear in parameters, they can be transformed into matrix form

$$ R \varvec{\beta} \geq 0, $$

(19)

where R is a matrix of dimension n × (1 + n (n + 3)/2) with

$$ R = \left[ \begin{array}{lllll} 0 & 1 & 0 & \ldots & 0 \\ 0 & 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \ \end{array}\begin{array}{lllll} \ln x_1 & \ln x_2 & \ldots & \ln x_n \\ 0 & \ln x_1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \ln x_1 \\ \end{array}\begin{array}{lllll}0 & \ldots & 0 & \ldots & 0 \\ \ln x_2 & \ldots & \ln x_n & \ldots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \ldots & \ln x_2 & \ldots & \ln x_n \\ \end{array}\right] $$

(20)

and

$$ \varvec{\beta} = \left( \beta_0, \beta_1, \beta_2, \ldots, \beta_n, \beta_{11}, \beta_{12}, \ldots, \beta_{1n}, \beta_{22}, \ldots, \beta_{2n}, \ldots, \beta_{nn} \right)^{\prime} $$

(21)

contains the linearly independent coefficients of the translog production function (15). Should the monotonicity condition be checked or imposed not at one but at T > 1 data points, the matrix R in Eq. 20 can be created for each data point and then all of these (sub)matrices can be stacked to a new R matrix with T · n rows.

Given that the monotonicity restrictions of the translog function are linear in parameters, the quadratic distance minimization in (10) can be converted to a usual quadratic programming problem

$$ \user2{s}^* = \mathop{\hbox{arg\,min}}\limits_{\user2{s}} \user2{c}^{\prime}\user2{s} + \frac{1}{2} \user2{s}^{\prime} Q \user2{s}, $$

(22)

$$ \hbox {s.t. } A \user2{s} \leq \user2{b}, $$

(23)

where $\user2{s} = \hat{\varvec{\beta}}^0 - \hat{\varvec{\beta}}$, $\user2{c} = ( 0, \ldots, 0 )$, $Q = 2 \hat{\varvec{\Upsigma}}_\beta^{-1}$, A = R, and $\user2{b} = - R \hat{\varvec{\beta}}$. After solving this quadratic programming problem, the restricted β coefficients can be obtained by $\hat{\varvec{\beta}}^0 = \user2{s}^* + \hat{\varvec{\beta}}$. Hence, this distance minimization can be done easily by any quadratic programming software.

As stated in Theorem 1 below, the translog functional form has the advantage that monotonicity can be easily imposed regionally, i.e. in a closed connected set of the input quantities.

Theorem 1 (Regional monotonicity of translog functions)

A translog function $f( \user2{x}, \varvec{\beta} )$ is monotonic in $\user2{x}$ on a closed connected set that consists of all $\ln \user2{x}$ in the convex polyhedron with vertices $\ln \user2{x}_1, \ldots, \ln \user2{x}_p,$ if and only if each of its partial derivatives retains the sign over all vertices:

$$ s_i f_i ( \user2{x}, \varvec{\beta} ) \geq 0 \quad \forall \quad i \in \left\{ 1, \ldots, n \right\}, \quad \user2{x} \in \left\{ \user2{x}_1, \ldots, \user2{x}_p \right\} $$

(24)

where

$$ s_i = \left\{\begin{array}{ll} 1 & \;\hbox {if } f(. ) \hbox { is monotonically increasing in } x_i\\ -1 & \;\hbox {if } f(. ) \hbox { is monotonically decreasing in } x_i\\ \end{array}\right. $$

(25)

The proof is given in Appendix 2.

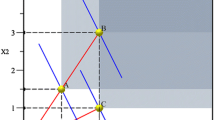
Theorem 1 implies that if the input quantities are measured in logarithmic terms, imposing monotonicity at the vertices of a convex polyhedron in the n-dimensional space of (logarithmic) input quantities ensures that monotonicity is fulfilled in the entire polyhedron.⁸ Hence, if monotonicity is imposed at all sample points, the monotonicity condition also is fulfilled on all points on the straight lines between each two sample points (given that input quantities are measured in logarithmic terms) and the problem of non-monotone intervals between sample points (as demonstrated in Fig. 2) is ruled out. If the input quantities are measured in natural (non-logarithmic) terms, monotonicity is imposed in a closed connected set of the input quantities but it is not a convex polyhedron because the edges of this set are not straight but rather they are curved. This is illustrated in Fig. 3.

Fig. 3

Imposing regional monotonicity of translog functions

Another option is to impose monotonicity at the vertices of a box (n-dimensional cuboid) that includes the region at which monotonicity should be imposed (e.g. all data points). The lower left vertex of this box should be (at most) at the position (min x ₁, minx ₂,…, minx _n ) and the upper right vertex of this box should be (at least) at the position (maxx ₁, maxx ₂,…, maxx _n ), where the edges of this box are parallel to the axes of the n-dimensional space of logarithmic input quantities. This ensures that the region at which monotonicity is imposed is also a box in the space of natural (non-logarithmic) input quantities. This is illustrated in Fig. 4.

If the unrestricted production frontier (9) is of the translog functional form, the adjusted restricted frontier function (14) is also of the translog form. Its coefficients can be calculated by

$$ \hat{\hat{\beta}}_0^0= \hat{\alpha}_0 + \hat{\alpha}_1 \hat{\beta}_0^0 $$

(26)

$$ \hat{\hat{\beta}}_i^0= \hat{\alpha}_1 \hat{\beta}_i^0 \; \forall \; i > 0 $$

(27)

$$ \hat{\hat{\beta}}_{ij}^0= \hat{\alpha}_1 \hat{\beta}_{ij}^0 \; \forall \; i, j, $$

(28)

where $\hat{\beta}_.^0$ are the restricted coefficients obtained from the distance minimization (10) and $\hat{\alpha}$ are the coefficients for adjusting the restricted production frontier estimated in the final stochastic frontier estimation (12).

Fig. 4

Imposing monotonicity of translog functions at a box

4 An empirical example

We demonstrate this method using panel data collected from 43 smallholder rice producers in the Tarlac region of the Philippines from 1990 to 1997. This data set is published as a supplement to Coelli et al. (2005).⁹ The data include one output (tons of freshly threshed rice) and three inputs: area planted (in hectares), labour used (in man-days of family and hired labour), and fertilizer used (in kg of active ingredients). We explain technical inefficiency according to the education of the household head (in years) and the percentage of area classified as “bantog” (upland) fields.

All estimations and calculations have been done within the “R software environment for statistical computing and graphics” (R Development Core Team 2009) using the “R” packages “frontier” (Coelli and Henningsen 2009), “micEcon” (Henningsen 2008), and “quadprog” (Turlach and Weingessel 2007). The commands that have been used for this analysis are available in Appendix 3.

The estimation results of the unrestricted stochastic frontier production function are presented in Table 1.¹⁰ The β and δ coefficients are defined as before, σ² is the total error variance ($\sigma^2_u + \sigma^2_v$), and γ is the proportion of the variance of technical inefficiency in the total error variance ($\sigma^2_u / \sigma^2$). The monotonicity condition is violated at 39 out of 344 observations and quasiconcavity is not fulfilled at four observations. While the education of the household head has no significant influence on technical efficiency, the proportion of “bantog” (upland) fields significantly (at the 10% level) increases the farm’s efficiency.

Table 1 Unrestricted stochastic frontier estimation

The coefficients obtained by the minimum distance estimation are presented in Table 2. Many coefficients have changed considerably (column “diff”), but all changes are less than two times the standard error of the first-step estimation (column “diff/std.err”). The last column (“adj.coef”) shows the restricted coefficients after adjusting the production frontier with α₀ and α₁ estimated in the final step. Of course, the monotonicity condition is fulfilled at all observations now. Moreover, the quasiconcavity condition also is fulfilled at all observations. Interestingly, we obtained the same result, i.e. imposing monotonicity implies quasiconcavity, also for other empirical applications (e.g. Wiebusch 2005; Henning and Mumm 2009; Henning and Han 2009). Barnett (2002) argues that imposing curvature but not monotonicity increases the incidence of monotonicity violations. Hence, imposing monotonicity first and checking for curvature thereafter—as in our approach—seems more effective than imposing curvature alone. However, monotonicity has a closer relationship to quasiconcavity than to concavity (see above) so that it is questionable if imposing monotonicity generally implies concavity in empirical applications.

Table 2 Minimum distance estimation

The results of the final SFA are presented in Table 3. As expected, the coefficient of the intercept is virtually zero and the coefficient of the “frontier output” is virtually one. Hence, the coefficients of the adjusted and non-adjusted restricted production frontier are almost identical (compare columns “coef” and “adj.coef” of Table 2). The effects of education and the proportion of “bantog” (upland) fields on technical efficiency are rather similar to the unrestricted model. The imposition of the monotonicity restriction caused an increase of the total error variance (σ²) from around 0.41 to 0.46. In contrast, the proportion of the variance of technical inefficiency in the total error variance (γ) does not change much.

Table 3 Final stochastic frontier estimation

We test the monotonicity restrictions by a Wald test and a likelihood ratio test. Both tests do not reject the monotonicity restrictions with P-values of 0.39 and 0.42, respectively.

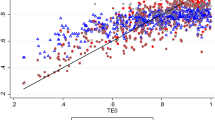
Figures 5, 6, and 7 illustrate the effect of imposing monotonicity on the partial production elasticities of the inputs. The estimates based the unrestricted and the restricted model are highly correlated with coefficients of correlation of 0.99, 0.97, and 0.99 for land, labor, and fertilizer, respectively. While the partial production elasticities of fertilizer are very similar in both models, imposing monotonicity reduces the average elasticity of land from 0.49 to 0.45 and increases the average elasticity of labor from 0.25 to 0.29. Furthermore, imposing monotonicity clearly reduces the ranges and variances of the partial production elasticities of land and labor, i.e. small values (including negative values) increase and large values decrease.

Fig. 5

Partial production elasticities of land. Note: the unfilled circles indicate observations with monotonicity violated in the unrestrestricted model

Fig. 6

Partial production elasticities of labor. Note: the unfilled circles indicate observations with monotonicity violated in the unrestrestricted model

Fig. 7

Partial production elasticities of fertilizer. Note: the unfilled circles indicate observations with monotonicity violated in the unrestrestricted model

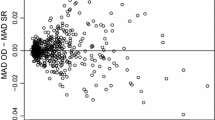
The efficiency estimates of the unrestricted and restricted models are contrasted in Fig. 8. The average technical efficiencies of the unrestricted (0.7749) and the restricted model (0.7744) are almost identical and most individual technical efficiencies of the restricted and unrestricted models are very similar (i.e. lying on the 45° line). However, a few technical efficiencies are considerably smaller in the theoretically consistent model, where the observations with the largest differences in the efficiency estimates are those with the monotonicity condition violated in the unrestricted model. Hence, the unrestricted model leads to some inconsistent efficiency estimates.

Fig. 8

Efficiency estimates of the restricted and unrestricted model. Note: the unfilled circles indicate observations with monotonicity violated in the unrestrestricted model

5 Conclusions

We have shown that efficiency estimates based on non-monotone frontier functions cannot be reasonably interpreted. Given the importance of monotonicity we suggest that non-monotone production frontiers should no longer be used in empirical production analysis, particularly since we have proposed a three-step procedure that is much simpler than existing approaches. We show that imposing monotonicity at one point is not sufficient to obtain reasonable efficiency estimates and we demonstrate how monotonicity of a flexible translog function can be imposed on a closed set (region) of input quantities. Our three-step method can be used to impose theoretical consistency not only on translog production frontiers but also on other functional forms and other frontier functions such as distance, cost, or profit frontiers. Although the theoretical restrictions for these functions are more complex than the monotonicity restrictions of a translog production frontier, our proposed three-step procedure still is probably less complex than a restricted ML or a Bayesian Markov chain Monte Carlo (MCMC) estimation.

Appendices

Appendices

1.1 Appendix 1: Distance minimization with $\varvec{\delta}$ parameters

It also is possible to include the $\varvec{\delta}$ parameters in the distance minimization (10, 11):

$$ \hat{\varvec{\theta}}^0= \hbox{arg\,min} \left( \hat{\varvec{\theta}}^0 - \hat{\varvec{\theta}} \right) \hat{\varvec{\Upsigma}}_\theta^{-1} \left( \hat{\varvec{\theta}}^0 - \hat{\varvec{\theta}} \right), $$

(29)

$$ \hbox {s.t. } f_i ( \user2{x}, \hat{\varvec{\theta}}^0 ) \geq 0 \; \forall \; i, \user2{x}, $$

(30)

where $\varvec{\theta} = ( \varvec{\beta}^{\prime}, \varvec{\delta}^{\prime})^{\prime}$. This approach also adjusts the $\varvec{\delta}$ coefficients, but both approaches result in identical restricted $\varvec{\beta}$ coefficients (see proof below). We suggest including only the $\varvec{\beta}$ coefficients in this minimization because $\varvec{\delta}$ coefficients based on a theoretically consistent frontier production function are obtained in the third step anyway.

1.1.1 Distance minimization of the β coefficients

$$ \beta^{0} = \hbox{arg}\min_{\beta^{0}} \left(\beta^{0}-\beta\right)^{\prime} \Upsigma_{11}^{-1}\left(\beta^{0}-\beta\right), $$

(31)

$$ \hbox {s.t. }R\beta^{0}\geq r $$

(32)

Lagrangian function

$$ L=\left(\beta^{0}-\beta\right)^{\prime}\Upsigma_{11}^{-1}\left (\beta^{0}-\beta\right)+\mu^{\prime}\left(r-R\beta^{0}\right) $$

(33)

Kuhn–Tucker conditions

$$ \frac{\partial L}{\partial\beta^{0}} = 2\Upsigma_{11}^{-1}\left(\beta^{0}-\beta\right)-R^{\prime}\mu=0 $$

(34)

$$ \mu \geq0 $$

(35)

$$ r-R\beta^{0} \leq 0 $$

(36)

$$ \mu\left(r-R\beta^{0}\right)= 0 $$

(37)

1.1.2 Distance minimization of the β and δ coefficients

$$ \left(\begin{array}{l}\beta^{0}\\\delta^{0}\\ \end{array}\right) =\hbox {arg}\min_{\beta^{0},\delta^{0}} \left(\begin{array}{l} \beta^{0}-\beta\\ \delta^{0}-\delta\\ \end{array}\right)^{\prime} \left[\begin{array}{ll}\Upsigma_{11} & \Upsigma_{12}\\ \Upsigma_{12}^{\prime} & \Upsigma_{22}\\ \end{array}\right]^{-1}\left(\begin{array}{ll} \beta^{0}-\beta\\ \delta^{0}-\delta\end{array}\right), $$

(38)

$$ \hbox {s.t. }R\beta^{0}\geq r $$

(39)

Lagrangian function

$$ L=\left(\begin{array}{ll} \beta^{0}-\beta\\ \delta^{0}-\delta\\ \end{array}\right)^{\prime}\left[ \begin{array}{ll} \Upomega_{11} & \Upomega_{12}\\ \Upomega_{12}^{\prime} & \Upomega_{22}\\ \end{array}\right]\left( \begin{array}{ll} \beta^{0}-\beta\\ \delta^{0}-\delta\\ \end{array}\right)+\mu^{\prime}\left(r-R\beta^{0}\right) $$

(40)

Kuhn–Tucker conditions

$$ \frac{\partial L}{\partial\left(\begin{array}{l} \beta^{0}\\ \delta^{0}\\ \end{array}\right)} = 2\left[\begin{array}{ll} \Upsigma_{11} & \Upsigma_{12}\\ \Upsigma_{12}^{\prime} & \Upsigma_{22}\\ \end{array}\right]^{-1}\left(\begin{array}{l} \beta^{0}-\beta\\ \delta^{0}-\delta\\ \end{array}\right)+\left(\begin{array}{ll} -R^{\prime}\mu\\ 0\\ \end{array}\right)=0 $$

(41)

$$ \mu \geq 0 $$

(42)

$$ r-R\beta^{0} \leq 0 $$

(43)

$$ \mu\left(r-R\beta^{0}\right)=0 $$

(44)

Equation 41 can be split into

$$ \frac{\partial L}{\partial\beta^{0}} = 2\Upomega_{11}\left(\beta^{0}-\beta\right)+ 2\Upomega_{12}\left(\delta^{0}-\delta\right)-R^{\prime}\mu=0 $$

(45)

$$ \frac{\partial L}{\partial\delta^{0}}= 2\Upomega_{21}\left(\beta^{0}-\beta\right)+2\Upomega_{22}\left (\delta^{0}-\delta\right)=0 $$

(46)

with

$$ \left[\begin{array}{ll} \Upomega_{11} & \Upomega_{12}\\ \Upomega_{22} & \Upomega_{22}\\ \end{array}\right]= \left[\begin{array}{ll} \Upsigma_{11} & \Upsigma_{12}\\ \Upsigma_{12}^{\prime} & \Upsigma_{22}\\ \end{array}\right]^{-1} $$

The inverse of this (partitioned) Σ matrix is

$$ \left[\begin{array}{ll}\Upomega_{11} & \Upomega_{12}\\ \Upomega_{21} & \Upomega_{22}\ \end{array}\right] = \left[\begin{array}{ll} \Upsigma_{11} & \Upsigma_{12}\\ \Upsigma_{12}^{\prime} & \Upsigma_{22}\\ \end{array}\right]^{-1} $$

(47)

$$ = \left[\begin{array}{ll} \Upsigma_{11}^{-1}+\Upsigma_{11}^{-1}\Upsigma_{12}Q^{-1}\Upsigma_{12}^{\prime}\Upsigma_{11}^{-1} & -\Upsigma_{11}^{-1}\Upsigma_{12}Q^{-1}\\ -Q^{-1}\Upsigma_{12}^{\prime}\Upsigma_{11}^{-1} & Q^{-1}\end{array}\right]\\ $$

(48)

$$ = \left[\begin{array}{ll} P^{-1} & -P^{-1}\Upsigma_{12}\Upsigma_{22}^{-1}\\ -\Upsigma_{22}^{-1}\Upsigma_{12}^{\prime}P^{-1} & \Upsigma_{22}^{-1}+\Upsigma_{22}^{-1}\Upsigma_{12}^{\prime}P^{-1}\Upsigma_{12} \Upsigma_{22}^{-1} \end{array}\right] $$

(49)

with Q = Σ₂₂−Σ ^′₁₂ Σ₁₁Σ₁₂ and $P=\Upsigma_{11}-\Upsigma_{12}\Upsigma_{22}^{-1}\Upsigma_{12}^{\prime}$ (Harville 1997, p. 99). From Eq. 46 we get

$$ \left(\delta^{0}-\delta\right)= -\Upomega_{22}^{-1}\Upomega_{21}\left(\beta^{0}-\beta\right) $$

(50)

Substituting this into (45) and applying (48) we get

$$ \frac{\partial L}{\partial\beta^{0}}= 2\Upomega_{11}\left(\beta^{0}-\beta\right)-2 \Upomega_{12}\Upomega_{22}^{-1}\Upomega_{21}\left(\beta^{0}-\beta\right)-R^{\prime}\mu=0 $$

(51)

$$ =2\left(\Upomega_{11}-\Upomega_{12}\Upomega_{22}^{-1} \Upomega_{21}\right)\left(\beta^{0}-\beta\right)-R^{\prime}\mu=0 $$

(52)

$$ =2\left(\Upsigma_{11}^{-1}+\Upsigma_{11}^{-1} \Upsigma_{12}Q^{-1}\Upsigma_{12}^{\prime} \Upsigma_{11}^{-1}-\Upsigma_{11}^{-1}\Upsigma_{12}Q^{-1} Q Q^{-1}\Upsigma_{12}^{\prime}\Upsigma_{11}^{-1}\right)\left(\beta^{0}-\beta\right)-R^{\prime}\mu=0 $$

(53)

$$ = 2\Upsigma_{11}^{-1}\left(\beta^{0}-\beta\right)-R^{\prime}\mu=0 $$

(54)

From Eq. 54 we get

$$ \left(\beta^{0}-\beta\right) = \frac{1}{2}\Upsigma_{11}R^{\prime}\mu $$

(55)

Substituting this into (46) and applying (49) we get

$$ \frac{\partial L}{\partial\delta^{0}} = \Upomega_{21}\Upsigma_{11}R^{\prime}\mu+2\Upomega_{22}\left(\delta^{0}-\delta\right)=0 $$

(56)

$$ =-\Upsigma_{22}^{-1}\Upsigma_{12}^{\prime}P^{-1} \Upsigma_{11}R^{\prime}\mu+2\left(\Upsigma_{22}^{-1}+ \Upsigma_{22}^{-1}\Upsigma_{12}^{\prime} P^{-1}\Upsigma_{12}\Upsigma_{22}^{-1} \right)\left(\delta^{0}-\delta\right)=0 $$

(57)

Hence, the Kuhn–Tucker conditions (41–44) can be re-written as

$$ \frac{\partial L}{\partial\beta^{0}} = 2\Upsigma_{11}^{-1}\left(\beta^{0}-\beta\right)-R^{\prime}\mu=0 $$

(58)

$$ \frac{\partial L}{\partial\delta^{0}} = -\Upsigma_{22}^{-1}\Upsigma_{12}^{\prime}P^{-1}\Upsigma_{11}R^{\prime}\mu+ 2\left(\Upsigma_{22}^{-1}+\Upsigma_{22}^{-1}\Upsigma_{12}^{\prime}P^{-1} \Upsigma_{12}\Upsigma_{22}^{-1}\right)\left(\delta^{0}-\delta\right)=0 $$

(59)

$$ \mu \geq 0 $$

(60)

$$ r-R\beta^{0} \leq 0 $$

(61)

$$ \mu\left(r-R\beta^{0}\right) = 0 $$

(62)

Because the Kuhn–Tucker conditions (58) and (60–62) are identical to the conditions (34–37) and Eq. 59 does not contain a β⁰, both minimization approaches result in the same values for β⁰.

1.2 Appendix 2: Proof of Theorem 1

Proof (Theorem 1)

The partial derivatives of a quadratic function

$$ g( \user2{w}, \varvec{\beta} ) = \alpha_0 + \sum_{i=1}^n \beta_i w_i + \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \beta_{ij} w_i w_j $$

(63)

evaluated at point $\user2{w}_k$ are

$$ g_i ( \user2{w}_k, \varvec{\beta} ) = \left. \frac{\partial g( \user2{w}, \varvec{\beta} )}{\partial w_i} \right|_{ \user2{w} = \user2{w}_k } = \beta_i + \sum_{j=1}^n \beta_{ij} w_{j,k}. $$

(64)

If we set $\user2{w}$ equal to $\ln \user2{x}$, the partial derivatives of the quadratic function evaluated at the point $\user2{w}_k = \ln \user2{x}_k$ become

$$ g_i ( \user2{w}_k, \varvec{\beta} ) = g_i ( \ln \user2{x}_k, \varvec{\beta} ) = \beta_i + \sum_{j=1}^n \beta_{ij} \ln x_{j,k} $$

(65)

Since $f( \user2{x}, \varvec{\beta} ) > 0$ and $x_1, \ldots, x_n \gg 0$, the partial derivatives of $f( \user2{x}, \varvec{\beta} )$ and $g ( \user2{w}, \varvec{\beta} )$ always have the same sign:

$$ \hbox{sgn} \left[ f_i ( \user2{x}, \varvec{\beta} ) \right]= \hbox{sgn}\left[ \frac{f( \user2{x}, \varvec{\beta} )}{x_i} \left( \beta_i + \sum_{j=1}^n \beta_{ij} \ln x_j \right) \right] $$

(66)

$$ \begin{aligned} = \hbox{sgn} \left[ \beta_i + \sum_{j=1}^n \beta_{ij} \ln x_j \right] = \hbox{sgn} \left[ g_i ( \ln \user2{x}, \varvec{\beta} ) \right] = \hbox{sgn} \left[ g_i ( \user2{w}, \varvec{\beta} ) \right]\\ \forall \quad \varvec{\beta}, \user2{w}= \ln \user2{x}, \hbox { and } i \in \left \{ 1, \ldots, n \right\} \end{aligned} $$

(67)

Hence, Eq. 24 implies that each of the partial derivatives of $g ( \user2{w}, \varvec{\beta} )$ retains the sign over a set of points $\user2{w}_1, \ldots, \user2{w}_p$, where $\user2{w}_k = \ln \user2{x}_k \forall k \in \{ 1,\ldots, p \}$:

$$ s_i \; g_i ( \user2{w}, \varvec{\beta} ) \geq 0 \quad \forall \quad i \in \left\{ 1, \ldots, n \right\}, \quad \user2{w} \in \left\{ \user2{w}_1, \ldots, \user2{w}_p \right\} $$

(68)

Tangian (2002, p. 134) shows that this implies that $g ( \user2{w}, \varvec{\beta} )$ is monotonic in $\user2{w}$ on the convex polyhedron P with vertices $\user2{w}_1, \ldots, \user2{w}_p$:

$$ s_i \; g_i ( \user2{w}, \varvec{\beta} ) \geq 0 \quad \forall \quad \user2{w} \in P( \user2{w}_1, \ldots, \user2{w}_p ) $$

(69)

This further implies that $f ( \user2{x}, \varvec{\beta} )$ is monotonic in $\user2{x}$, if $\ln \user2{x}$ is in the convex polyhedron with vertices $\ln \user2{x}_1, \ldots, \ln \user2{x}_p$:

$$ s_i \; f_i ( \user2{x}, \varvec{\beta} ) \geq 0 \quad \forall \quad \user2{x} \hbox { with } \ln \user2{x} \in P( \ln \user2{x}_1, \ldots, \ln \user2{x}_p ) $$

(70)

□

1.3 Appendix 3: Source code

1.3.1 Commands used for the estimation

The following commands have been used to estimate a theoretically consistent stochastic frontier production function:

1.3.2 Commands to display the results

The following commands can be used to display the estimation results.

1.3.2.1 Unrestrcited stochastic frontier estimation (step 1)

1.3.2.2 Minimum distance estimation (step 2)

1.3.2.3 Final stochastic frontier estimation (step 3)

1.3.2.4 Testing monotonicity restrictions

1.3.2.5 Partial production elasticities of the restricted and the unrestricted model

1.3.2.6 Efficiency estimates of the restricted and the unrestricted model