Bifurcation scenarios in the hardware-in-the-loop experiments of highly interrupted milling processes

Abstract

Hardware-in-the-loop (HIL) measurements of highly interrupted milling processes were conducted. A real spindle was used with a dummy tool on which the cutting forces were emulated with contactless sensors and actuators. During the experiments, Hopf- and period-doubling bifurcations were identified. The nonlinear dynamics of these period-doubling bifurcations are analyzed for a discrete model of highly interrupted milling. This investigation found the bifurcation to be subcritical, which draws the attention to the limited practical validity of linear stability analysis.

1 Introduction

The main limiting factor of efficiency and productivity in machining operations is the occurrence of regenerative vibrations (called chatter), which can increase wear on machine tools and produce intolerable machined surface quality [1]. One approach to limiting these harmful vibrations is the design of milling tools with irregular geometry [2]. The manufacturing of these tools themselves is a complex process making their design and prototyping expensive and time-consuming. The HIL environment allows for the emulation of cutting forces related to any tool geometry and material property without a need for prototyping.

It has previously been shown that the HIL system developed in [3] is capable of reproducing the Hopf-bifurcation-related self-excited vibrations in turning processes and the inherent nonlinearities of the actuation of this HIL system have also been studied. The emulation of the real nonlinear dynamics of milling processes is yet to be implemented in this HIL system; however, the approximation of the linear terms alone was sufficient for the detection of stability boundaries and for the identification of possible bifurcation scenarios.

It is well known that the Hopf-bifurcations in machining operations are subcritical, which is critical because large enough perturbations can disrupt the linearly stable machining process [4,5,6]. It was shown in [7] for a discrete model of highly interrupted cutting that the period-doubling bifurcations are also subcritical. A similar discrete nonlinear model is investigated in this paper with a detailed analytic approximation of the resulting unstable limit cycles, which also involves the migration of the center of the limit cycles. This is significant in determining the parameter setup of the so called fly-over effect when the tool loses contact with the workpiece and further non-smooth nonlinear effects appear.

2 Motivation and HIL experiments

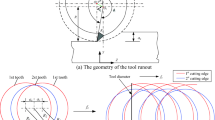
A highly interrupted down-milling process is investigated with a simple straight edge milling tool at low radial immersion. The corresponding mechanical model is shown in Fig. 1.

Fig. 1

Mechanical model of milling operations

The parameters m, c and k are the mass, damping and stiffness describing the relevant modal behavior of the machine tool. The $Z=3$-tooth milling tool has diameter D, and the spindle speed is given by $\varOmega$ in rotations per minute. Parameters a (axial depth-of-cut), r (radial depth-of-cut) and v (feed rate) determine the material removal rate. The equation of motion describing this 1 degree of freedom oscillator is derived in [8]:

$$\begin{aligned} \ddot{x}(t)+2\zeta \omega _{\textrm{n}}\dot{x}(t)+\omega _{\textrm{n}}^2x(t){=}&\frac{aK_{\textrm{s}}(t)}{m}\nonumber \\&\quad (h_{0}{+}x(t-\tau ){-}x(t)), \end{aligned}$$

(1)

where $h_{0}=v\tau$ is the desired chip thickness and $K_{\textrm{s}}(t)$ is the specific cutting force variation determined by the radial immersion (r/D) and the experimentally determined material properties. The delay parameter $\tau =60/(Z\varOmega )$ is the time period of the tooth-pass. The angular natural frequency is $\omega _{\textrm{n}}=\sqrt{k/m}$, damping ratio is $\zeta =c/(2m\omega _{\textrm{n}})$, and damped natural frequency is $\omega _{\textrm{d}}=\omega _{\textrm{n}}\sqrt{1-\zeta ^2}$. These modal parameters were carefully identified for the investigated experimental HIL system leading to the relevant natural frequency [3]

$$\begin{aligned} f_{\textrm{d}}=\omega _{\textrm{d}}/(2\pi )=3056\,\text {Hz and } \zeta =1.98\,\%. \end{aligned}$$

(2)

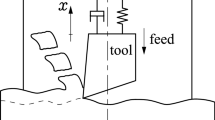
In the HIL environment, the oscillations of a dummy tool in a real spindle were measured at different axial depth-of-cuts and spindle speeds at $1\%$ radial immersion. The position of the dummy tool is measured with a laser based sensor. The emulated force is updated at up to a 100 kHz frequency using a low inductance coil.

Fig. 2

Components of the HIL system

This high frequency is needed to follow the sudden changes related to the teeth entering and/or leaving the material. The sketch of the HIL system can be seen in Fig. 2. The original and discretized specific cutting force variations are presented in Fig. 3.

Fig. 3

Specific cutting force variation and its emulation in the HIL system

The oscillations of the dummy tool were measured at each axial depth-of-cut and spindle speed combination. The stability boundaries were determined based on the resulting vibration amplitudes. The result of the measurements can be seen in Fig. 4 panel a), compared to the stability boundaries predicted by the semi-discretization method [9]. The stability regions show good agreement of the calculations and the measurements.

For the experimental identification of the bifurcations, the frequency content of the measured oscillations was used (Fig. 4 panel b).

Fig. 4

Theoretical and experimental stability chart and waterfall diagram for the HIL system emulating a milling process

In the region of the left-side lobe, the dominant regenerative vibration frequency is close to the natural frequency of the dummy tool with no linear dependence on the spindle speed $\varOmega$, which is in accordance with the presence of Hopf-bifurcation. The right-side lobe shows period-doubling frequencies, which are linearly dependent on the spindle speed and are harmonics of the half of the tooth-pass frequency. The results of these measurements show that the HIL system is capable of emulating real milling processes by capturing the period-doubling bifurcations that are unique to milling processes, besides the Hopf-bifurcations appearing also in simple turning processes.

3 Mechanical model of highly interrupted cutting

In highly interrupted machining operations, the amount of time the tool spends in contact with the material, compared to free-flight is small, which is characterized by the parameter $\rho \ll 1$ giving the ratio of cutting to not cutting in time. This allows for the approximation of the motion as combinations of free-flights of length $\tau$ and impact-like short cutting segments [7].

The simplest mechanical model of highly interrupted cutting and its relation to the continuous milling process (1) through the specific cutting force variation can be seen in Fig. 5; in this case, the ratio $\rho$ can be determined directly from the specific cutting force variation.

Fig. 5

Mechanical model of highly interrupted cutting

Let us introduce the notation

$$\begin{aligned} x_{j}=x(t_{j})=x(j\tau )\quad j=0,1,2\dots \end{aligned}$$

(3)

for state variables immediately after the impact-like cutting and let $x^{-}_{j}$ denote variables immediately before impact.

Since the short cutting segment is treated as an instantaneous impact, the position of the tool does not change ($x_{j}=x^{-}_{j}$) and the change in velocity is related to the impulse of the cutting force alone, as the inertial forces have negligible effect in such a short time. This means that the linear cutting force characteristics may be described simply with a constant $K_{1}$ (see Fig. 5) such that its integral over $\rho \tau$ is the same as that of the specific cutting force variation

$$\begin{aligned} K_{1}=\frac{1}{\rho \tau }\int \limits _{(1-\rho )\tau }^{\tau }K_{\textrm{s}}(t)\textrm{d}t. \end{aligned}$$

(4)

The nonlinear cutting force can be calculated using the instantaneous chip thickness h and the experimentally verified 3/4 rule [10]

$$\begin{aligned} F(h)={\text {Cah}}^{3/4}={\text {Ca}}(h_{0}+x_{j-1}-x_{j})^{3/4}. \end{aligned}$$

(5)

The linear term $K_{1}$ was identified as opposed to parameter C; however, the Taylor-series of (5) can be determined around $h=h_{0}$

$$\begin{aligned} F(h) \approx&{\text {Cah}}_{0}^{3/4}+\frac{3{\text {Ca}}}{4h_{0}^{1/4}}(x_{j-1}-x_{j})\nonumber \\&-\frac{3{\text {Ca}}}{32h_{0}^{5/4}}(x_{j-1}-x_{j})^{2}\nonumber \\ {}&+\frac{5{\text {Ca}}}{128h_{0}^{9/4}}(x_{j-1}-x_{j})^{3}\dots \nonumber \\&= \frac{4}{3}K_{1}{\text {ah}}_{0}+K_{1}a(x_{j-1}-x_{j})\nonumber \\&-\frac{K_{1}a}{8h_{0}}(x_{j-1}-x_{j})^{2}\nonumber \\ {}&+\frac{5K_{1}a}{96h_{0}^2}(x_{j-1}-x_{j})^{3}\dots . \end{aligned}$$

(6)

According to Eq. (6), the velocity change during the impact simplifies to

$$\begin{aligned}&m(\dot{x}_{j}-\dot{x}^{-}_{j})=\int \limits _{(1-\rho )\tau }^{\tau }F(h)\textrm{d}t, \end{aligned}$$

(7)

that is,

$$\begin{aligned} m(v_{j}-v^{-}_{j})&=\rho \tau \frac{4}{3}K_{1}ah_{0}+\rho \tau K_{1}a(x_{j-1}-x_{j})\nonumber \\&\quad -\rho \tau \frac{K_{1}a}{8h_{0}}(x_{j-1}-x_{j})^{2}\nonumber \\ {}&\quad +\rho \tau \frac{5K_{1}a}{96h_{0}^2}(x_{j-1}-x_{j})^{3}. \end{aligned}$$

(8)

The free-flight segment of the motion of the milling tool is simply governed by the equation

$$\begin{aligned} \ddot{x}(t)+2\zeta \omega _{\textrm{n}}\dot{x}(t)+\omega _{\textrm{n}}^2x(t)=0\,,\ t \in [t_{j}-\tau ,t_{j}-\rho \tau ). \end{aligned}$$

(9)

For a single $\tau$-length period of free-flight and cutting, we may start with initial conditions $x_{j-1}$ and $v_{j-1}$ and calculate the solution of Eq. (9) to get

$$\begin{aligned}&x(t_{j-1}+(1-\rho )\tau ) \approx x(t_{j-1}+\tau )=x^{-}_{j}=x_{j},\nonumber \\&v(t_{j-1}+(1-\rho )\tau ) \approx v(t_{j-1}+\tau )=v^{-}_{j}. \end{aligned}$$

(10)

Then use Eq. (8) to get the velocity after the impact:

$$\begin{aligned} v_{j}&=v^{-}_{j}+\frac{4\rho \tau }{3m}K_{1}ah_{0}+\frac{\rho \tau }{m} K_{1}a(x_{j-1}-x_{j})\nonumber \\&\quad -\frac{\rho \tau }{m}\frac{K_{1}a}{8h_{0}}(x_{j-1}-x_{j})^{2}\nonumber \\&\quad +\frac{\rho \tau }{m}\frac{5K_{1}a}{96h_{0}^2}(x_{j-1}-x_{j})^{3}. \end{aligned}$$

(11)

This can all be done in closed form to get the nonlinear discrete model of highly interrupted cutting

$$\begin{aligned} \begin{bmatrix} x_{j+1} \\ v_{j+1} \end{bmatrix}= & {} \textbf{A} \begin{bmatrix} x_{j} \\ v_{j} \end{bmatrix}+\begin{bmatrix} 0 \\ \sum \limits _{p+q=2,3; p,q \ge 0}b_{pq}x^{p}_{j}v^{q}_{j} \end{bmatrix}\nonumber \\{} & {} +\begin{bmatrix} 0 \\ \frac{4\rho \tau }{3m}K_{1}ah_{0} \end{bmatrix}, \end{aligned}$$

(12)

where the matrix describing the linear part $\textbf{A}$ takes the form

$$\begin{aligned} \textbf{A}=\begin{bmatrix} A_{11} &{}&{} A_{12} \\ A_{21} &{}&{} A_{22} \end{bmatrix}. \end{aligned}$$

(13)

Introducing the phase parameter $\varepsilon$ by $\tan \varepsilon$$=\zeta /\sqrt{1-\zeta ^2}$, the coefficients of matrix $\textbf{A}$ become

$$\begin{aligned}{} & {} A_{11}=\frac{e^{-\zeta \omega _{\textrm{n}}\tau }}{\sqrt{1-\zeta ^2}}\cos (\omega _{\textrm{d}}\tau -\varepsilon ),\nonumber \\{} & {} A_{12}=\frac{e^{-\zeta \omega _{\textrm{n}}\tau }}{\omega _{\textrm{n}}\sqrt{1-\zeta ^2}}\sin (\omega _{\textrm{d}}\tau ),\nonumber \\{} & {} A_{21}=-\frac{\omega _{\textrm{n}}e^{-\zeta \omega _{\textrm{n}}\tau }}{\sqrt{1-\zeta ^2}}\sin (\omega _{\textrm{d}}\tau )\nonumber \\{} & {} \quad \quad \quad +\frac{\rho \tau }{m}K_{1}a\left( 1-\frac{e^{-\zeta \omega _{\textrm{n}}\tau }}{\sqrt{1-\zeta ^2}}\cos (\omega _{\textrm{d}}\tau -\varepsilon )\right) ,\nonumber \\{} & {} A_{22}{=}\frac{e^{{-}\zeta \omega _{\textrm{n}}\tau }}{\sqrt{1{-}\zeta ^2}}\left( \cos (\omega _{\textrm{d}}\tau {+}\varepsilon ){-}\frac{\rho \tau }{m\omega _{\textrm{n}}}K_{1}a\sin (\omega _{\textrm{d}}\tau ) \right) .\nonumber \\ \end{aligned}$$

(14)

4 Period-doubling bifurcation

The stability of highly interrupted milling in Eq. (12) can simply be determined based on the eigenvalues of matrix $\textbf{A}$, while the fixed point $(x^{*}, y^{*})$ is given by

$$\begin{aligned} \begin{bmatrix} x^{*} \\ y^{*} \end{bmatrix} = (\textbf{I}-\textbf{A})^{-1} \begin{bmatrix} 0 \\ \frac{4\rho \tau }{3m}K_{1}ah_{0} \end{bmatrix}. \end{aligned}$$

(15)

This fixed point in the discrete system corresponds to a $\tau$-periodic steady-state motion in time.

Considering a period-doubling bifurcation, we may assume that one of the eigenvalues of $\textbf{A}$ is $\lambda _{1}=-1$. In this case, the other eigenvalue and the critical axial depth-of-cut can be derived as

$$\begin{aligned} \lambda _{1}= & {} -1,\nonumber \\ \lambda _{2}= & {} e^{-\zeta \omega _{\textrm{n}}\tau }\left( \sinh (\zeta \omega _{\textrm{n}}\tau )+\cos (\omega _{\textrm{d}}\tau )\right) , \end{aligned}$$

(16)

and

$$\begin{aligned} a_{\textrm{cr}}=\frac{m\omega _{\textrm{d}}}{\rho \tau K_{1}}\frac{\cosh (\zeta \omega _{\textrm{n}}\tau )+\cos (\omega _{\textrm{d}}\tau )}{\sin (\omega _{\textrm{d}}\tau )}. \end{aligned}$$

(17)

This closed-form result for the stability map may be compared with the one provided by the semi-discretization method for the continuous model (1) (see Fig. 6).

Fig. 6

Stability chart of the discrete model of highly interrupted cutting

The stable domain predicted by this discrete model is somewhat larger than it is for the continuous model given with the numerical results of the semi-discretization method; however, the placement of the lobes and the types of bifurcations match well.

In order to investigate this period-doubling bifurcation, we may introduce a bifurcation parameter $\mu$ as

$$\begin{aligned} a=a_{\textrm{cr}}+\mu , \end{aligned}$$

(18)

which corresponds to the crossing of the stability boundary seen in Fig. 6. The eigenvectors corresponding to the eigenvalues in (16) are

$$\begin{aligned}&\mathbf {s_{1}}=\begin{bmatrix} \sin (\omega _{\textrm{d}}\tau ) \\ -\omega _{\textrm{n}}\cos (\omega _{\textrm{d}}\tau -\varepsilon )-\omega _{\textrm{d}}e^{\zeta \omega _{\textrm{n}}\tau } \end{bmatrix},\nonumber \\&\mathbf {s_{2}}=\begin{bmatrix} \frac{1}{\omega _{\textrm{n}}}\sin (\omega _{\textrm{d}}\tau ) \\ -\zeta \sin (\omega _{\textrm{d}}\tau )+\sqrt{1-\zeta ^2}\sinh (\zeta \omega _{\textrm{n}}\tau ) \end{bmatrix}. \end{aligned}$$

(19)

Using this eigenbasis, the modal transformation matrix $\mathbf {T_{cr}}$ and modal coordinates $\xi$ and $\eta$ for the critical parameters may be defined:

$$\begin{aligned} \mathbf {T_{cr}}=\begin{bmatrix} \mathbf {s_{1}}&\,&\mathbf {s_{2}} \end{bmatrix}, \ \ \ \ \ \ \begin{bmatrix} x \\ y \end{bmatrix}=\mathbf {T_{cr}}\begin{bmatrix} \xi \\ \eta \end{bmatrix}. \end{aligned}$$

(20)

This transformation is applied for Eq. (12), and its combination with a shifting in accordance with Eq. (15) results in the equation

$$\begin{aligned} \begin{bmatrix} \xi _{j+1} \\ \eta _{j+1} \end{bmatrix} = \mathbf {B_{cr}} \begin{bmatrix} \xi _{j} \\ \eta _{j} \end{bmatrix}+\begin{bmatrix} \sum \limits _{p+q=2,3; p,q \ge 0}c_{pq}\xi ^{p}_{j}\eta ^{q}_{j} \\ \sum \limits _{p+q=2,3; p,q \ge 0}d_{pq}\xi ^{p}_{j}\eta ^{q}_{j} \end{bmatrix},\nonumber \\ \end{aligned}$$

(21)

where

$$\begin{aligned} \mathbf {B_{cr}}=\begin{bmatrix} -1 &{}&{} 0 \\ 0 &{}&{} \lambda _{2} \end{bmatrix}. \end{aligned}$$

(22)

The two-dimensional problem (21) can be extended with a parameter dimension $\mu _{j+1}=1\cdot \mu _{j}$ and as such be divided into a two-dimensional center subspace, spanned by $\xi$ and $\mu$, corresponding to $\lambda _{1}=-1$, $\lambda _{\mu }=1$ critical eigenvalues and a stable subspace, spanned by $\eta$, corresponding to the stable eigenvalue $|\lambda _{2}| < 1$. For some value of the bifurcation parameter $\mu$, the modal transformation takes the form

$$\begin{aligned} \begin{bmatrix} x \\ y \end{bmatrix}=\textbf{T}(\mu )\begin{bmatrix} \xi \\ \eta \end{bmatrix}, \end{aligned}$$

(23)

and

$$\begin{aligned} \begin{bmatrix} \xi _{j+1} \\ \eta _{j+1} \end{bmatrix} {=} \textbf{B}(\mu ) \begin{bmatrix} \xi _{j} \\ \eta _{j} \end{bmatrix}\!{+}\!\begin{bmatrix} \sum \limits _{p+q=2,3; p,q \ge 0}C_{pq}(\mu )\xi ^{p}_{j}\eta ^{q}_{j} \\ \sum \limits _{p+q=2,3; p,q \ge 0}D_{pq}(\mu )\xi ^{p}_{j}\eta ^{q}_{j} \end{bmatrix}\!,\nonumber \\ \end{aligned}$$

(24)

where

$$\begin{aligned} \textbf{B}(\mu )=\begin{bmatrix} -1+\beta (\mu ) &{}&{} 0 \\ 0 &{}&{} \varLambda _{2}(\mu ) \end{bmatrix}. \end{aligned}$$

(25)

We may then construct an approximation of the center manifold tangent to the center subspace, such that the solutions of Eq. (24) converge to this manifold [11]

$$\begin{aligned} \eta =H(\xi ,\mu )=H_{20}\xi ^2+H_{11}\xi \mu +H_{02}\mu ^2. \end{aligned}$$

(26)

The coefficients of this quadratic formulation are calculated by finding the values for which restricting the motion to the center manifold fulfills the two equations of (24). First, $\eta _{j}=H(\xi _{j},\mu )$ and $\eta _{j+1}=H(\xi _{j+1},\mu )$ are substituted into Eq. (24). Then the Taylor-series approximation of the $\mu$ dependent terms is used, for which the zeroth-order terms are the parameters defined in Eqs. (21) and (22). Finally, only terms of up to the second order of $\xi _{j}$ and $\mu$ are kept. The polynomial balance of these terms results in the coefficients

$$\begin{aligned} H_{20}=\frac{d_{20}}{1-\lambda _{2}},\quad H_{11}=0,\quad H_{02}=0, \end{aligned}$$

(27)

where

$$\begin{aligned} d_{20}{=}{-}\frac{\omega _{\textrm{n}}}{2h_{0}}\frac{\sin (\omega _{\textrm{d}}\tau )\left( \cos (\omega _{\textrm{d}}\tau )+\cosh (\zeta \omega _{\textrm{n}}\tau )\right) }{\cos (\omega _{\textrm{d}}\tau ){+}\cosh (\zeta \omega _{\textrm{n}}\tau ){+}2\sinh (\zeta \omega _{\textrm{n}}\tau )}.\nonumber \\ \end{aligned}$$

(28)

After restriction to the center manifold, the dynamical system is described by

$$\begin{aligned} \xi _{j+1}=g_{1}(\mu )\xi _{j}+g_{2}(\mu )\xi _{j}^2+g_{3}(\mu )\xi _{j}^3+\mathcal {O}(\xi _{j}^4), \end{aligned}$$

(29)

where

$$\begin{aligned}&g_{1}(\mu )=-1+\beta (\mu ), \nonumber \\&g_{2}(\mu )=C_{20}(\mu ), \nonumber \\&g_{3}(\mu )=C_{30}(\mu )+C_{11}(\mu )H_{20}. \end{aligned}$$

(30)

The second degree term can be eliminated from Eq. (29) using the near identity transformation

$$\begin{aligned} \xi =u+f_{2}(\mu )u^2, \end{aligned}$$

(31)

where

$$\begin{aligned} f_{2}(\mu )=\frac{g_{2}(\mu )}{g_{1}^2(\mu )-g_{1}(\mu )}, \end{aligned}$$

(32)

resulting in

$$\begin{aligned} u_{j+1}=\left( -1+\beta (\mu )\right) u_{j}+\delta (\mu )u_{j}^3. \end{aligned}$$

(33)

The coefficient $\delta (\mu )$ in Eq. (33) is similar in role to the Poincaré–Lyapunov constant in Hopf-bifurcations and determines the criticality of the period-doubling bifurcation. Let us assume that the sign of $\delta (\mu )$ does not change for any $\mu$ sufficiently close to the critical point. In this way, the zeroth-order Taylor-series approximation may be used to determine its sign:

$$\begin{aligned}&f_{20}=f_{2}(0)=\frac{c_{20}}{2},\nonumber \\&\delta _{0}=\delta (0)=c_{20}^2+c_{30}+c_{11}\frac{d_{20}}{1-\lambda _{2}}. \end{aligned}$$

(34)

We can see that all of the terms in Eq. (34) are parameters defined in Eqs. (21) and (22) at the critical point. After some algebraic manipulations, $f_{20}$ and $\delta _{0}$ can be given as

$$\begin{aligned}&f_{20}=\frac{1}{4h_{0}}\frac{\sin (\omega _{\textrm{d}}\tau )\left( \cos (\omega _{\textrm{d}}\tau )+\cosh (\zeta \omega _{\textrm{n}}\tau )\right) }{\cos (\omega _{\textrm{d}}\tau )+\cosh (\zeta \omega _{\textrm{n}}\tau )+2\sinh (\zeta \omega _{\textrm{n}}\tau )},\nonumber \\&\delta _{0}=-\frac{5}{12h_{0}^2}\frac{\sin ^2(\omega _{\textrm{d}}\tau )(\cos (\omega _{\textrm{d}}\tau )+\cosh (\zeta \omega _{\textrm{n}}\tau ))}{\cos (\omega _{\textrm{d}}\tau )+\cosh (\zeta \omega _{\textrm{n}}\tau )+2\sinh (\zeta \omega _{\textrm{n}}\tau )}\nonumber \\&\qquad <0, \end{aligned}$$

(35)

where the result for $\delta _{0}$ agrees with the one presented in [12], while the new formula for $f_{20}$ will become relevant during the identification of the periodic solutions. The $\delta _{0}$ parameter is always negative, which leads to the bifurcation being subcritical. The simplest way to find the approximation of the unstable limit cycle related to this bifurcation is to perform one more scaling transformation in Eq. (33)

$$\begin{aligned} u=\frac{1}{\sqrt{|\delta (\mu )|}}w. \end{aligned}$$

(36)

Making use of $\delta (\mu )<0$, transformation (36) results in

$$\begin{aligned} w_{j+1}&=\left( -1+\beta (\mu )\right) w_{j}-w_{j}^3. \end{aligned}$$

(37)

Using the Taylor-series approximation

$$\begin{aligned} \beta (\mu )=\beta (0)+\frac{\textrm{d}\beta }{\textrm{d}\mu }(0)\mu +\mathcal {O}(\mu ^2), \end{aligned}$$

(38)

Eq. (37) has a $2\tau$-periodic solution for

$$\begin{aligned} w_{j}^2=\beta _{1}\mu +\mathcal {O}(\mu ^2). \end{aligned}$$

(39)

Here, $\beta _{1}$ is a parameter still to be determined. However, this is simply related to the change of the critical eigenvalue for a given $\mu$ and can be calculated from the linear system alone. Let us investigate matrix $\textbf{A}$ for a given parameter $\mu$

$$\begin{aligned} \textbf{A}(\mu )=\begin{bmatrix} A_{11}^{\textrm{cr}} &{}&{} A_{12}^{\textrm{cr}} \\ A_{21}^{\textrm{cr}}+\mu \alpha _{21} &{}&{} A_{22}^{\textrm{cr}}+\mu \alpha _{22} \end{bmatrix}, \end{aligned}$$

(40)

where $A_{ij}^{\textrm{cr}}$ are the elements of $\textbf{A}$ at $\mu =0$. Constructing the characteristic equation for the eigenvalue $-1+\beta (\mu )$ and noticing that $-1$ fulfills this equation for $\mu =0$, we find

$$\begin{aligned} \beta ^2(\mu )&-(2+\mu \alpha _{22}+A_{22}^{\textrm{cr}}+A_{11}^{\textrm{cr}})\beta (\mu )\nonumber \\&+\mu \alpha _{22}(A_{11}^{\textrm{cr}}+1)-\mu \alpha _{21}A_{12}^{\textrm{cr}}=0. \end{aligned}$$

(41)

Differentiation of Eq. (41) by $\mu$ results in

$$\begin{aligned}&\frac{\textrm{d}\beta (\mu )}{\textrm{d}\mu }=\frac{\alpha _{22}(\beta (\mu )-1-A_{11}^{\textrm{cr}})+\alpha _{21}A_{12}^{\textrm{cr}}}{2(\beta (\mu )-1)-\mu \alpha _{22}-A_{22}^{\textrm{cr}}-A_{11}^{\textrm{cr}}},\nonumber \\&\beta _{1}=\frac{\textrm{d}\beta }{\textrm{d}\mu }(0)=\frac{\alpha _{22}(A_{11}^{\textrm{cr}}+1)-\alpha _{21}A_{12}^{\textrm{cr}}}{2+A_{22}^{\textrm{cr}}+A_{11}^{\textrm{cr}}}<0. \end{aligned}$$

(42)

After some algebraic manipulation, we find

$$\begin{aligned} \beta _{1}{=}{-}\frac{2\rho \tau K_{1}}{m\omega _{\textrm{d}}}\frac{\sin (\omega _{\textrm{d}}\tau )}{\cos (\omega _{\textrm{d}}\tau ){+}\cosh (\zeta \omega _{\textrm{n}}\tau ){+}2\sinh (\zeta \omega _{\textrm{n}}\tau )},\nonumber \\ \end{aligned}$$

(43)

which is always negative. This means that the dynamical system described by w has a solution

$$\begin{aligned} w_{k}=(-1)^{k}\sqrt{\beta _{1}\mu }. \end{aligned}$$

(44)

Now, we can reverse the transformations (36), (31) and (23) approximated with their zeroth-order Taylor-series in $\mu$, to find the approximation of the limit cycle amplitude in the order of $\sqrt{\mu }$ and the approximation of the center of the limit cycle in the order of $\mu$:

$$\begin{aligned}&u_{k}=(-1)^k\sqrt{\frac{-\beta _{1}}{\delta _{0}}\mu \,},\nonumber \\&\xi _{k}=(-1)^k\sqrt{\frac{-\beta _{1}}{\delta _{0}}\mu \,}+f_{20}\left( \frac{-\beta _{1}}{\delta _{0}}\right) \mu ,\nonumber \\&x_{k}=(-1)^k\sin (\omega _{\textrm{d}}\tau )\sqrt{\frac{-\beta _{1}}{\delta _{0}}\mu \,}\nonumber \\&\quad \quad +\sin (\omega _{\textrm{d}}\tau )\left( \frac{-\beta _{1}}{\delta _{0}}\right) \left( f_{20}+\frac{H_{20}}{\omega _{\textrm{n}}}\right) \mu . \end{aligned}$$

(45)

The result (45) means that there exists an unstable limit cycle in the linearly stable parameter domain. This is a critical case from engineering viewpoint since the machining process might be disrupted by a large enough perturbation of the system even for (linearly) stable cutting parameters.

In order to verify these results numerically, simulations were conducted. This could be done relatively simply considering that (12) is a discrete system. The initial conditions for these simulations were close to the center manifold; thus, the point where the initial conditions become large enough for the solution to diverge corresponds to initial conditions just “outside” the limit cycle calculated in Eq. (45). The results of these simulations can be seen in Fig. 7, and the estimates match well for both the amplitudes and the offset of the center of the limit cycles.

Fig. 7

Simulated and analytic unstable limit cycles

This subcritical behavior describes the dynamics of highly interrupted cutting well as long as the tool is still able to make cuts with all its cutting edges. Once the displacements are large enough for any of the cutting edges to pass over the workpiece, fly-over occurs, that is, the instantaneous chip thickness $h(t_{k})=h_{0}+x_{k-1}-x_{k}$ becomes zero, or virtually negative. Formula (45) provides another critical bifurcation parameter $\mu ^{*}<0$, and a related new critical axial depth-of-cut

$$\begin{aligned} a^{*}=a_{cr}-\frac{\delta _{0}h_{0}^2}{4\beta _{1}\sin ^2(\omega _{\textrm{d}}\tau )}, \end{aligned}$$

(46)

where fly-over first occurs with the unstable limit cycle. In this calculation, the center of the limit cycle determined by $f_{20}$ does not appear; however, it affects the conservative estimation of the allowable perturbation (see Fig. 8):

$$\begin{aligned} |\varDelta x|\le \frac{1}{2}h_{0}-\left| \frac{f_{20}+\frac{H_{20}}{\omega _{\textrm{n}}}}{4\sin (\omega _{\textrm{d}}\tau )}\right| h_{0}^2\,. \end{aligned}$$

(47)

For depth-of-cut $a<a^{*}$, the fly-over effect erases the unstable $2\tau$-periodic motion and makes the steady-state cutting globally stable.

Fig. 8

Analytical prediction of unstable limit cycles of the period-doubling bifurcation and the fly-over effect for $h_{0}=10\,$ $\mu$m

5 Conclusions

Highly interrupted machining processes were investigated. First, a HIL experiment was conducted, which was able to reproduce both the Hopf and period-doubling bifurcations present in milling operations. Then a discrete nonlinear model of highly interrupted cutting was analyzed. Using this model, it was shown that the period-doubling bifurcations are subcritical. The developed closed form expressions for the unstable periodic motion provides an efficient method to accurately estimate the parameter region where the fly-over effect appears.