1 Introduction

The dependence of the nonlinear transversal behaviour of beams on different axial boundary conditions is an interesting topic that has been studied by various authors. In [1], it was shown that a beam is hardening if the axial displacement is constrained at the boundary and is softening if the boundary is free to move axially. These findings were confirmed in [2], where a refined reduced order model analysis was performed, and the effect of the axial inertia and inextensibility was investigated.

A fully continuous model was considered in [3], where the multiple time scales method is applied directly to the partial differential equations of motion. The results were also compared with some experiments. On the same line of investigation, [4] considered an axial (i.e. parametric) excitation, and developed the asymptotic analysis up to the fifth order, i.e. one order more than what is usually done. Also some experimental results were reported.

In fact, it is known that axial inertia contributes to softening, while the geometrical stiffness, which is strongly affected by the axial constraint, contributes to hardening. The whole behaviour depends on which one of these two opposite phenomena predominates. Thus, it is possible to foresee that introducing at the boundary a spring, of stiffness \(\kappa \), which allows us to regulate the axial constraint and thus the geometrical nonlinearity, permits to control the hardening/softening behaviour, passing from softening when \(\kappa =0\) (no constraint) to hardening when \(\kappa \rightarrow \infty \) (full constraint), that are the limit cases reported in the earlier literature [1, 2].

Although a boundary axial spring is present in [3] and [4], its effect on the softening/hardening behaviour is not fully investigated there. This has been done, instead, in [5], where the dependence of the nonlinear correction coefficient \(\omega _2\) (\(\omega _2>0\) gives hardening, \(\omega _2<0\) provides softening) upon \(\kappa \) is deeply investigated. There, also the effects of the axial and rotational inertia have been studied, as well as those of the shear stiffness and slenderness. A Timoshenko beam model was considered to have reliable results also for thick beams.

Starting from [6], where the equations of motions were firstly derived and initially analyzed by means of the Poincaré–Lindstedt method, and [5], the authors have done many studies on this topic. In [7], the approximate analytical results have been compared with numerical simulations to check their reliability. In these papers, attention was focused on the transversal oscillations, and the axial vibrations are set equal to zero to the first order and appear only to the second order because of the nonlinear coupling. Actually, this hypothesis has been relaxed in [8], where the axial vibrations to the first order have been considered, too, and the coupling between axial and transversal oscillations is deeply investigated. Interesting, and complex, behaviour charts have been reported, showing that coupled and uncoupled solutions can coexist or not, both being hardening or softening.

The difference obtained by considering alternative definitions of the curvature (geometric, i.e. \(\frac{\mathrm{d}\theta }{\mathrm{d}S}\), vs mechanical, i.e. \(\frac{\mathrm{d}\theta }{\mathrm{d}Z}\), dS and dZ being the infinitesimal elements of the deformed and undeformed configurations, respectively) in the constitutive behaviour has been the subject of [9] and [10]. It has been shown that the difference is of the order of some percents for thick beams and is totally negligible for slender beams.

While in the previous authors’ work free vibrations have been considered, in [11] and [12] the forced vibrations have been investigated. In [11], the multiple time scales method has been used, and again the attention was focused on the dependence of the hardening/softening response on the spring stiffness \(\kappa \). Analytical results have been compared with numerical (FEM) results, showing a good agreement up to moderately large displacements, according to the fact that analytical solution is valid only up to the third order. The appearance of some superharmonic and internal resonances has been observed in the numerical simulations. Still in the forced regime, the comparison between numerical and experimental results was instead the goal of [12], where a very good matching has been observed.

The frequency response curves of higher order resonances have been discussed in [13], where, among other, it has been stressed that the nonlinear behaviour may strongly depend on the mode order, for example the first mode can be hardening and the second softening.

Within this wide body of research, one aspect has not yet been investigated, namely the internal resonance between axial and transversal modes. Indeed, in [8] it was assumed that axial and transversal modes were far away from internal resonance, so that the axial–transversal coupling was only due to the nonlinear effects occurring in kinematically non-condensed structural models (e.g. [14]). Here, on the contrary, this hypothesis is relaxed, and the internal resonance is fully investigated, both in the linear and nonlinear regimes. In addition to its theoretical and practical effects, this also permits to explain a singularity of the nonlinear correction coefficient observed in [5] and in [11]. As discussed in more detail in Sect. 2.1 forward, a similar singular behaviour of the nonlinear correction coefficient, associated with the transition from hardening to softening and due to an internal resonance, has been earlier highlighted in shallow cables [15, 16] and in shells [17, 18], where only transversal dynamics have been studied.

A transition from hardening to softening, due to 1 : 2 internal resonance and not necessarily related to a singular behaviour, has been observed also in a pipe conveying fluid [19], where the varying parameter was the fluid velocity, and in a double beam with a tip coupling spring and magnetic interaction [20], where the driving parameters were the amplitude of the excitation and the damping.

Internal resonance, or modal interactions [21], have been deeply investigated in the past [22,23,24], since this event can be dangerous (if not properly detected [25]) or useful (if properly exploited, for example in the field of energy harvesting [26]). However, it seems that few attention has been paid to the internal resonance between longitudinal and flexural modes. Axial–transversal internal resonances of cables have been investigated, for example, in [27, 28], of moving belts in [29], while for beams this phenomenon has been investigated in [30], again in the field of axially moving systems. Very few investigations of internal longitudinal–transversal resonance seem to be available for non-moving beams [31].

The paper is organized as follows. The mechanical model is illustrated in Sect. 2, including a summary of previous results (Sect. 2.1) where the singularity of the nonlinear frequency \(\omega _2\) is highlighted. The occurrence of various axial–transversal internal resonances in the slenderness-spring stiffness parameters space is investigated in Sect. 3 in the linear regime. Then (Sect. 4), attention is focused on 1:2 internal resonance, but now a nonlinear dynamic analysis is developed with the multiple time scales method. The main results are reported in Sect. 5, while a comparison of analytical and numerical outcomes is presented in Sect. 6. The paper ends with some conclusions and suggestions for further developments (Sect. 7).

2 The mathematical model

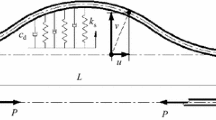
We consider the Timoshenko beam illustrated in Fig. 1. Its rest configuration is rectilinear, along the Z direction, it is made of a linearly elastic and homogeneous material, and its cross section is constant. W(Z, T), U(Z, T) and \(\theta (Z,T)\) are the axial and transversal displacements of the beam axis, and the rotation of the cross section. Z is the spatial coordinate in the reference (straight) configuration, measuring the physical distance from the left boundary, and T is the time.

The axial, shear and bending stiffnesses are EA, GA and EJ, respectively. The axial and transversal mass per unit length is \(\rho A\), while the rotational inertia is \( \rho J\). \(\kappa \) is the stiffness of the linear spring at the right-end of the beam (Fig. 1), which acts in the Z (axial) direction. \(C_W\), \(C_U\) and \(C_{\theta }\) are the (linear) damping coefficients along the respective directions. The beam is excited by a dead load \(P_U(Z,T)=F(Z,T)\) acting in the X direction, which is perpendicular to Z. Introducing axial, \(P_W(Z,T)\), and rotational, \(P_{\theta }(Z,T)\), loads is conceptually easy but will not be pursued to limit the computational efforts.

Fig. 1
figure 1

Timoshenko beam with axial end spring

Full size image

The kinematically exact equations of motion have been derived in [6] (see also [5, 8, 11]) and are given by:

$$\begin{aligned}&\left\{ EA [\sqrt{(1+W')^2+U'^2}-1] \frac{1+W'}{\sqrt{(1+W')^2+U'^2}} \right. \nonumber \\&\qquad \left. + GA \left[ \theta - \arctan \left( \frac{U'}{1+W'}\right) \right] \frac{U'}{\sqrt{(1+W')^2+U'^2}} \right\} ' \nonumber \\&\quad = \rho A \, \ddot{W} + C_W \dot{W}, \nonumber \\&\left\{ EA [\sqrt{(1+W')^2+U'^2}-1] \frac{U'}{\sqrt{(1+W')^2+U'^2}} \right. \nonumber \\&\qquad \left. - GA \left[ \theta - \arctan \left( \frac{U'}{1+W'}\right) \right] \frac{1+W'}{\sqrt{(1+W')^2+U'^2}} \right\} ' \nonumber \\&\quad =\rho A \, \ddot{U} + C_U \dot{U} + F(Z,T), \nonumber \\&\left[ EJ \frac{\theta '}{\sqrt{(1+W')^2+U'^2}} \right] ' \nonumber \\&\qquad - GA \left[ \theta - \arctan \left( \frac{U'}{1+W'}\right) \right] \sqrt{(1+W')^2+U'^2}\nonumber \\&\quad =\rho J \, \ddot{\theta } + C_{\theta } \dot{\theta }, \end{aligned}$$
(1)

where the prime denotes derivative with respect to Z and dot derivative with respect to T.

The boundary conditions in the transversal direction are:

$$\begin{aligned}&U(0,T)=0, \quad M(0,T)=0, \nonumber \\&U(L,T)=0, \quad M(L,T)=0, \end{aligned}$$
(2)

where M is the bending moment,

$$\begin{aligned} M= & {} EJ \frac{\mathrm{d} \theta }{\mathrm{d}S} = EJ \frac{\mathrm{d}\theta }{\mathrm{d}Z} \frac{\mathrm{d}Z}{\mathrm{d}S}\nonumber \\= & {} EJ \frac{\theta '}{S'} = EJ \frac{\theta '}{\sqrt{(1+W')^2+U'^2}}, \end{aligned}$$
(3)

i.e. the geometrical curvature is considered. A possible alternative is to use the mechanical curvature, assuming \(M = EJ \frac{\mathrm{d}\theta }{\mathrm{d}Z}\) [9, 10].

The boundary conditions in the axial direction are:

$$\begin{aligned} W(0,T)=0, \quad H_o(L,T) + \kappa W(L,T)=0, \end{aligned}$$
(4)

where \(H_o(Z,T)\) is the internal horizontal force in the Z direction and is given by

$$\begin{aligned} H_o= & {} EA \frac{\sqrt{(1+W')^2+U'^2}-1}{\sqrt{(1+W')^2+U'^2}}(1+W')\nonumber \\&+\, GA \frac{\theta - \arctan \left( \frac{U'}{1+W'} \right) }{\sqrt{(1+W')^2+U'^2}} U'. \end{aligned}$$
(5)

2.1 Previous results

By applying the Poincaré–Lindstedt method (in [5, 6]) and the multiple time scales method (in [11]), and by considering only the transversal displacements up to the first order, the following approximate solution was previously obtained for the free oscillations:

$$\begin{aligned} W(Z,T)&=0 + \cdots , \nonumber \\ U(Z,T)&=U_a \, \sin \left( \frac{n \, \pi \, Z}{L} \right) \sin (\omega _f T)+\cdots , \nonumber \\ \theta (Z,T)&=\frac{U_a}{L} \left( n \, \pi - \frac{\omega _0^2}{n \, \pi \, z \, l^2} \right) \nonumber \\&\quad \times \, \cos \left( \frac{n \, \pi \, Z}{L} \right) \sin \left( \omega _f T\right) +\cdots , \end{aligned}$$
(6)

where \(U_a\) is the amplitude of the transversal motion, \(n \in \mathbb {N}\) the mode number, and where, most importantly,

$$\begin{aligned} \omega _f= & {} \omega _{f0} + \left( \frac{U_a}{L} \right) ^2 \omega _{f2} +\cdots \nonumber \\= & {} \frac{1}{L^2} \sqrt{\frac{EJ}{\rho A}} \left[ \omega _0 + \left( \frac{U_a}{L} \right) ^2 \omega _2 +\cdots \right] \end{aligned}$$
(7)

is the nonlinear frequency of the free motion.

In (7), \(\omega _0\) is the dimensionless natural (linear) frequency of the transversal motion, while \(\omega _2\) is the dimensionless nonlinear correction coefficient, also known as “nonlinear frequency correction”, which measures how the nonlinear frequency is affected by the amplitude of the motion. It was the most important result, since it summarizes the nonlinear behaviour of the system: hardening for \(\omega _2>0\), softening for \(\omega _2<0\).

For the boundary conditions (2), it is possible to compute

$$\begin{aligned} \omega _0 = \frac{l}{2}\sqrt{ z l^2 + n^2 \pi ^2 (1+z)- \sqrt{z^2 l^4 + 2 z n^2 \pi ^2 (1+z) l^2 + n^4 \pi ^4 (1- z)^2 } }, \end{aligned}$$
(8)

where \(n \in \mathbb {N}\) is the order of the transversal (flexural) natural frequency and the following three dimensionless parameters are introduced:

$$\begin{aligned} l = L \sqrt{\frac{EA}{EJ}}, \quad z = \frac{GA}{EA} = \frac{1}{2(1+\nu ) \chi }, \quad \kappa _\mathrm{h} = \frac{L^3}{EJ} \kappa , \end{aligned}$$
(9)

(l is the slenderness of the beam, \(\nu \) the Poisson coefficient and \(\chi \) the shear correction factor) so that

$$\begin{aligned} EA = \frac{EJ }{L^2} l^2, \quad \rho J = \frac{\rho A \, L^2}{l^2}, \quad GA = \frac{EJ }{L^2} l^2 z. \end{aligned}$$
(10)

\(\kappa _\mathrm{h}\) is the dimensionless stiffness of the axial spring at \(Z=L\), that will be used in the rest of the paper. We consider \(\nu =0.3\) and \(\chi =1.17\), namely \(z=0.3287\), so that the unique parameters are l and \(\kappa _\mathrm{h}\), together with the order n of the natural frequency.

For the same boundary conditions, the nonlinear correction coefficient is

$$\begin{aligned} \omega _2 = \frac{c_1 \omega _{2a} + c_2 \sin \left( 2 \omega _0 /l \right) \omega _{2b} + \omega _{2c} }{\omega _{2d}}, \end{aligned}$$
(11)

where the parameters appearing in (11) are reported in “Appendix”.

For \(\kappa _\mathrm{h}=50\) and \(n=1\), the function \(\omega _2(l)\) is plotted in Fig. 2, which corresponds to Fig. 10b of [5].

Fig. 2
figure 2

The function \(\omega _2(l)\) for \(\kappa _\mathrm{h}=50\) and \(n=1\)

Full size image

For the scope of the present work, the most relevant property of Fig. 2 is that \(\omega _2(l)\) has a singular point for \(l_\mathrm{sing}=8.149112\). It has also a zero point at \(l_\mathrm{zero}=11.379729\). When crossing these points, the sign of \(\omega _2\) changes, and, for increasing l, we pass from hardening to softening and again to hardening.

The singular and zero points are not specific of the considered value of \(\kappa _\mathrm{h}\), but they persist, as shown in Fig. 3, corresponding to Fig. 12c of [5].

Fig. 3
figure 3

The zero (continuous line) and singular (dash line) values of \(\omega _2\) for \(n=1\). The dots are the points corresponding to Fig. 2, where \(\kappa _\mathrm{h}=50\)

Full size image

In [5], eq. (27), looking at the expressions of \(\omega _2\), it was noted that the singular points occur when

$$\begin{aligned} \kappa _\mathrm{h}= -2\, l\,\omega _0 \frac{\cos \left( 2\, \omega _0/l \right) }{ \sin \left( 2\, \omega _0/l \right) }, \end{aligned}$$
(12)

namely when the denominator of \(c_2\) is zero. This phenomenon was also observed in [11], and in [32] it is mentioned that it is due to an internal resonance between axial and transversal modes. Confirming this property in the considered mechanical system, and studying in depth the internal resonances, is the main goal of this paper.

Before to proceed, we note that the singular points in Fig. 3 occur for quite low values of the slenderness (thick beams, but still compatible with the Timoshenko beam theory). Actually, for \(n=2\) the singular points happen for larger values of l (in the realm of slender beams), as shown by the example of Fig. 4, which corresponds to Fig. 3 of [11] (but note that a different rescaling of the spring stiffness is used there) and to a beam with square cross section and length equal to 10 times the thickness. Here, \(\kappa _{h,sing}=1661.24\) and \(\kappa _{h,zero}=2122.32\).

Fig. 4
figure 4

The function \(\omega _2(\kappa _\mathrm{h})\) for \(l=10 \sqrt{12}=34.6410\) and \(n=2\)

Full size image

For \(n=2\), the zero and singular points are reported in Fig. 5. Note that in this parameters window there are two singularities and zeros. The lowest zero and singular curves almost coincide. If one would enlarge the view, more singular and zero branches would appear.

Fig. 5
figure 5

The zero (continuous lines) and singular (dash lines) values of \(\omega _2\) for \(n=2\). The dots are the points corresponding to Fig. 4, where \(l=10 \sqrt{12}=34.6410\)

Full size image

Although the motivation of the present paper comes mainly from the authors’ previous work summarized above, it is worth mentioning that the singular behaviour of the nonlinear correction coefficient in correspondence of internal resonances, and in particular 1 : 2 internal resonance, has been previously observed for different mechanical systems in the framework of the reduction methods evaluation.

In [15], the singularity has been reported for the first in-plane (vertical) mode of a suspended cable. Here, the varying parameter is an elasto-geometric parameter taking into account stiffness and sag-to-span ratio, and the singularity is due to the breakdown of modal expansions not explicitly considering the internal resonance. For the same structure, a similar, but deeper, analysis has been reported in [16], where also the out-of-plane behaviour has been considered. Here, it is shown that discretized approaches, where the Galerkin reduction method is applied before the MTS, fail to detect the singular behaviour if a sufficiently large number of modes is not considered.

Using nonlinear normal modes to highlight hardening/softening behaviour of nonlinear systems [33], the singular behaviour of the nonlinear correction coefficient for a free-edge shallow spherical shell has been shown in [17], where the driving parameter is the aspect ratio, which is governed by the geometrical properties of the system. Within a study of the effect of the number of retained modes in a Galerkin reduction, many curves similar to Figs. 2 and 4 have been reported. It is remarked that only 1 : 2 internal resonance of certain modes are able to generate the singular behaviour, while other modes and other resonances (e.g. 1 : 3) do not have this effect. In [18], it has been shown that the addition of damping will smooth the singular behaviour, while keeping the large (but finite) values of \(\omega _2\) for small values of damping.

In the previous papers, the singular behaviour, and the 1 : 2 internal resonance lurking in the background, have been reported. However, a detailed asymptotic expansion considering the internal resonance is not carried out. This analysis has been done in [19, 20], where, however, no singular behaviour is observed in the background. In the present work, we complete, and somehow connect, the two groups of works, while referring to the longitudinal–transverse coupling in the mechanical system of our interest.

3 Longitudinal–transversal internal resonance: linear analysis

The occurrence of the longitudinal–transversal internal resonance in the parameters space \((\kappa _\mathrm{h, l})\) can be detected in the linear regime, where the two modal problems are independent from each other (since the beam is rectilinear). This constitutes the aim of this section. The nonlinear coupling in the neighbourhood of internal resonances will be investigated in the next section.

The transversal natural frequency \(\omega _{f0}\) is given (in dimensionless form) by (8). The axial natural frequency \(\omega _{a0}\), the solution of

$$\begin{aligned}&EA \, w''(Z) + \omega _{a0}^2 \, \rho A \, w(Z)=0, \nonumber \\&w(0)=0, \quad EA \, w'(L)+\kappa \, w(L)=0, \end{aligned}$$
(13)

can be easily computed by standard methods (see also Sect. 4.1) and is given by

$$\begin{aligned} \omega _{a0} = \frac{x}{L} \sqrt{\frac{EA}{\rho A}} = \frac{x \, l}{L^2} \sqrt{\frac{EJ}{\rho A}}, \end{aligned}$$
(14)

x being the solution of

$$\begin{aligned} x \, l^2 \, \cos (x) + \sin (x) \kappa _\mathrm{h} =0. \end{aligned}$$
(15)

The associated mode shape is \(w(Z)=\sin (x \,Z/L)\). Note that for very small values of \(\kappa _\mathrm{h}/l^2\) the solutions of (15) are \(x_m \cong \pi /2 + (m-1) \pi \), \(m \in \mathbb {N}\) being the order of the axial natural frequency, while for very large values of \(\kappa _\mathrm{h}/l^2\) the solutions of (15) are \(x_m \cong m \pi \). Thus, for varying \(\kappa _\mathrm{h}/l^2 \in [0,\infty [\) the following bounds hold: \(\pi /2 + (m-1) \pi \le x_m \le m \pi \).

The expression (15) can be rewritten as

$$\begin{aligned} \kappa _\mathrm{h}= - l^2 \, x \, \frac{\cos (x)}{\sin (x)}. \end{aligned}$$
(16)

When \(x = 2 \omega _{0} / l\), namely when \(\omega _{a0}=2 \, \omega _{f0}\), equation (16) is identical to (12), and this clearly shows that the singular points of \(\omega _2\) are due to the 1 : 2 internal resonance between transversal and axial modes.

Reasoning in a similar fashion, it is not difficult to foresee that singular points of \(\omega _4\) (the next term in the development (7)) will be due to a 1:4 internal resonance between transversal and axial modes and so on. This aspect will not be pursued here and is left for future works.

To generalize the previous considerations, we investigate the 1 : ir internal resonances, those such that

$$\begin{aligned} \frac{\omega _{a0}}{\omega _{f0}}=ir, \quad ir \in \mathbb {N}. \end{aligned}$$
(17)

The study of other internal resonances, for example \(2 \, \omega _{a0}=\omega _{f0}\), is left for future works.

Combining (7), (8), (14), (16) and (17), it is easy to obtain

$$\begin{aligned} \kappa _{h,ir}(l)= - l \, ir \, \omega _0 \, \frac{\cos (ir \, \omega _0/l)}{\sin (ir \, \omega _0/l)}. \end{aligned}$$
(18)

For \(ir=1;2;3\), the loci of internal resonance in the parameter space \((\kappa _\mathrm{h},l)\) are reported in Fig. 6, where n is the order of the transversal natural frequency, see (8). To understand the order m of the axial frequency, for each considered value of l, the lowest value of \(\kappa _\mathrm{h}\) is associated with the first axial mode, the next to the second and so on. For example, for \(ir=1\) (Fig. 6a) and for \(l=20\) we have that for \(\kappa _\mathrm{h}=75.0464380\) (point A) there is a 1:1 internal resonance between the second (because \(n=2\)) transversal mode and the first axial mode (so that \(m=1\)); for \(\kappa _\mathrm{h}=829.704872\) (point B) there is 1:1 internal resonance between the fourth (because \(n=4\)) transversal mode and the second axial mode (so that \(m=2\)).

In Fig. 6b, the point C corresponds to the case of Fig. 2: here, we have a 1 : 2 internal resonance between the first (\(n=1\)) transversal mode and the first axial mode (\(m=1\)). The point D corresponds to the case of Fig. 4: here, we have a 1 : 2 internal resonance between the second (\(n=2\)) transversal mode and the first axial mode (\(m=1\)). Note that, for the same value of \(\kappa _\mathrm{h}\), there is another 1 : 2 internal resonance between the second transversal mode and the first axial mode on the lower \(n=2\) curve, for \(l=5.7977\).

Fig. 6
figure 6

The loci of internal resonance. a \(ir=1\) (i.e. \(\omega _{f0}:\omega _{a0}=1:1\)), b \(ir=2\) (i.e. \(\omega _{f0}:\omega _{a0}=1:2\)), c and d \(ir=3\) (i.e. \(\omega _{f0}:\omega _{a0}=1:3\)). n is the order of the transversal frequency. (Color figure online)

Full size image

We notice that internal resonances are more sensitive to the slenderness l than to the spring stiffness \(\kappa _\mathrm{h}\). In fact, at least in the considered range of parameters and irrespective of the value of ir, internal resonances occur only for “fixed” values of l (or in narrow intervals of l), and there are large intervals of l (sort of “band gaps”) without internal resonances. On the contrary, they occur for every value of \(\kappa _\mathrm{h}\).

To end this section, we note that by varying the transversal boundary conditions (for example assuming fixed instead of hinged left boundary condition, \(\theta (0,T)=0\) instead of \(M(0,T)=0\) in (2)), the axial frequencies do not change, while the transversal ones are shifted. This permits to conclude that the same internal resonances observed in this section are expected to exist also for other boundary conditions, and they are only translated in the parameters space. The check of this guess is left for future work.

4 1 : 2 internal resonance: nonlinear analysis

In this section, we study, in the nonlinear regime, the 1 : 2 internal resonance illustrated in Fig. 6b, via an asymptotic analysis up to second order. In addition to its interest in explaining the singularities of the nonlinear correction coefficient \(\omega _2\), it has an interest “per se”, since this resonance has interesting dynamical behaviours, as we will see. The detailed nonlinear investigations of other internal resonances can be done analogously.

The multiple time scales (MTS) method [34] is used, by considering to the first order both axial and transversal modes. Also, in [11] the MTS was used, but there only the transversal mode is considered to the first order, so precluding the possibility to detect internal resonance (that was not the goal of that paper, indeed). Axial and transversal modes to the first order are also considered in [8], but there it is implicity assumed that they are not in internal resonance, since the aim was to detect the axial–transversal nonlinear coupling in a general fashion, and not only around specific values of the parameters where internal resonance occurs.

With the MTS method, the solution is sought after in the asymptotic form

$$\begin{aligned} W(Z,T)&=\varepsilon W_1(Z,T_0,T_1) + \varepsilon ^2 W_2(Z,T_0,T_1) +\cdots , \nonumber \\ U(Z,T)&=\varepsilon U_1(Z,T_0,T_1) + \varepsilon ^2 U_2(Z,T_0,T_1) + \cdots , \nonumber \\ \theta (Z,T)&=\varepsilon \theta _1(Z,T_0,T_1) + \varepsilon ^2\theta _2(Z,T_0,T_1) +\cdots , \end{aligned}$$
(19)

where \(\varepsilon \) is a bookeeping small parameter introduced to stress that we are studying moderate displacements and rotation around the rest position. \(T_0=T\) is the physical (fast) time, and \(T_i=\varepsilon ^i \, T\), \(i\ge 1\) are the slow times.

It is further assumed that the excitation is harmonic in time (with frequency \(\Omega \)), and that damping and load scale according to

$$\begin{aligned} C_W= & {} \varepsilon c_W, \quad C_U = \varepsilon c_U, \nonumber \\ C_{\theta }= & {} \varepsilon c_{\theta }, \quad F(Z,T)=\varepsilon ^2 f(Z) \cos (\Omega T). \end{aligned}$$
(20)

Inserting the expressions (19)–(20) in the asymptotic expansion of the governing equations (1), and equating to zero the coefficients of \(\varepsilon ^i\), a sequence of linear problems is derived. They are investigated in the next subsections.

4.1 First-order problem

The first-order equations read

$$\begin{aligned}&EA \, W_1''- \rho A \, \frac{\partial ^2 W_1}{\partial T_0^2} =0, \nonumber \\&GA ( \theta _1'-U_1'') + \rho A \, \frac{\partial ^2 U_1}{\partial T_0^2}=0, \nonumber \\&EJ \, \theta _1'' - GA (\theta _1-U_1') - \rho J \, \frac{\partial ^2 \theta _1}{\partial T_0^2}=0, \end{aligned}$$
(21)

and the related boundary conditions are (the dependence on time is omitted for simplicity)

$$\begin{aligned} W_1(0)&=0, \quad EA \, W_1'(L) + \kappa \, W_1(L)=0, \nonumber \\ U_1(0)&=0, \quad \theta _1'(0) = 0, \nonumber \\ U_1(L)&=0, \quad \theta _1'(L) = 0. \end{aligned}$$
(22)

The solution of (21), (22) is given by (the over bar stands for complex conjugate and I is the imaginary unit)

$$\begin{aligned} W_1(Z,T_0,T_1)&= W_{1a}(Z) [B(T_1) e^{I \omega _{a0} T_0}\nonumber \\&\quad +\,\bar{B}(T_1) e^{-I \omega _{a0} T_0} ], \nonumber \\ U_1(Z,T_0,T_1)&= U_{1a}(Z) [A(T_1) e^{I \omega _{f0} T_0}\nonumber \\&\quad +\, \bar{A}(T_1) e^{-I \omega _{f0} T_0} ], \nonumber \\ \theta _1(Z,T_0,T_1)&= \theta _{1a}(Z) [A(T_1) e^{I \omega _{f0} T_0} +\nonumber \\&\quad +\, \bar{A}(T_1) e^{-I \omega _{f0} T_0} ], \end{aligned}$$
(23)

where the functions \(W_{1a}(Z)\), \(U_{1a}(Z)\) and \(\theta _{1a}(Z)\) are reported in “Appendix”, and \(A(T_1)\) and \(B(T_1)\) are complex amplitudes of the transversal and axial oscillations, respectively. \(\omega _{a0}\) is given by (14) (with x given by (15)), while \(\omega _{f0}\) is given by (7) with \(\omega _0\) given by (8).

Note that in [5,6,7, 9, 11], but not in [8], it was assumed \(W_{1a}(Z)=0\).

4.2 Second-order problem

The second-order equations read

$$\begin{aligned}&EA \, W_2''- \rho A \, \frac{\partial ^2 W_2}{\partial T_0^2}\nonumber \\&\quad =c_W \, \frac{\partial W_1}{\partial T_0} + 2 \, \rho A \, \frac{\partial ^2 W_1}{\partial T_0 T_1}\nonumber \\&\qquad - \left[ (EA/2-GA) \, U_1'^2 + GA U_1' \theta _1\right] ', \nonumber \\&GA \left( \theta _2'-U_2''\right) + \rho A \, \frac{\partial ^2 U_2}{\partial T_0^2} \nonumber \\&\quad =-c_U \, \frac{\partial U_1}{\partial T_0} - 2 \, \rho A \, \frac{\partial ^2 U_1}{\partial T_0 T_1}\nonumber \\&\qquad +\, f(Z) \cos (\Omega T_0)+(EA-GA)(U_1' W_1')', \nonumber \\&EJ \, \theta _2'' - GA (\theta _2-U_2') - \rho J \, \frac{\partial ^2 \theta _2}{\partial T_0^2} \nonumber \\&\quad = c_{\theta } \, \frac{\partial \theta _1}{\partial T_0}\nonumber \\&\qquad +\, 2 \, \rho J \frac{\partial ^2 \theta _1}{\partial T_0 T_1} + GA \, W_1' \theta _1 + EJ (W_1' \theta _1')', \end{aligned}$$
(24)

and the related boundary conditions are (the dependence on time is omitted for simplicity)

$$\begin{aligned} W_2(0)&=0, \quad EA \, W_2'(L) + \kappa \, W_2(L)\nonumber \\&=-(EA/2-GA) U_1'^2(L) - GA U_1'(L) \theta _1(L), \nonumber \\ U_2(0)&=0, \quad \theta _2'(0) = 0, \nonumber \\ U_2(L)&=0, \quad \theta _2'(L) = 0. \end{aligned}$$
(25)

It is now necessary to introduce the 1 : 2 internal resonance condition,

$$\begin{aligned} \omega _{a0}= 2 \omega _{f0} + \varepsilon \sigma _i \rightarrow \omega _{a0} T_0 = 2 \omega _{f0} T_0 + \sigma _i T_1, \end{aligned}$$
(26)

together with the external resonance,

$$\begin{aligned} \Omega = \omega _{f0} + \varepsilon \sigma _e \rightarrow \Omega T_0 = \omega _{f0} T_0 + \sigma _e T_1, \end{aligned}$$
(27)

where \(\sigma _i\) and \(\sigma _e\) are the detuning parameters measuring the distance (in the frequency) from the perfect internal and external resonances, respectively. Note that, combining (26) and (27), we have

$$\begin{aligned} 2 \Omega = \omega _{a0} + \varepsilon (2 \sigma _e - \sigma _i), \end{aligned}$$
(28)

so that the detuning between \(2\Omega \) and \(\omega _{a0}\) is given by \((2 \sigma _e - \sigma _i)\).

The particular solution of (24) is given by

$$\begin{aligned} W_2(Z,T_0,T_1)&=W_{2a}(Z,T_1) e^{I \omega _{a0} T_0}\nonumber \\&\quad + \bar{W}_{2a}(Z,T_1) e^{-I \omega _{a0} T_0} \nonumber \\&\quad + W_{2b}(Z,T_1), \nonumber \\ U_2(Z,T_0,T_1)&=U_{2a}(Z,T_1) e^{I \omega _{f0} T_0}\nonumber \\&\quad + \bar{U}_{2a}(Z,T_1) e^{-I \omega _{f0} T_0} \nonumber \\&\quad + U_{2b}(Z,T_1) e^{3 I \omega _{f0} T_0}\nonumber \\&\quad + \bar{U}_{2b}(Z,T_1) e^{-3 I \omega _{f0} T_0}, \nonumber \\ \theta _2(Z,T_0,T_1)&=\theta _{2a}(Z,T_1) e^{I \omega _{f0} T_0}\nonumber \\&\quad + \bar{\theta }_{2a}(Z,T_1) e^{-I \omega _{f0} T_0} \nonumber \\&\quad + \theta _{2b}(Z,T_1) e^{3 I \omega _{f0} T_0}\nonumber \\&\quad + \bar{\theta }_{2b}(Z,T_1) e^{-3 I \omega _{f0} T_0}. \end{aligned}$$
(29)

It is worth to note that the homogenous solution of (24), that adds to (29), is not needed in this work.

Inserting (29) in (24), and in the boundary conditions, we obtain the following problems for \(W_{2a}(Z)\), \(U_{2a}(Z)\) and \(\theta _{2a}(Z)\):

$$\begin{aligned}&EA \, W_{2a}'' + \omega _{a0}^2 \, \rho A \, W_{2a} \nonumber \\&\quad = -f_W' e^{-I \sigma _{i} T_1} A(T_1)^2 \nonumber \\&\qquad + I \omega _{a0} W_{1a} \left[ 2 \rho A \frac{\mathrm{d} B}{\mathrm{d} T_1}(T_1)+ c_W B(T_1) \right] , \nonumber \\&W_{2a}(0)=0, \quad EA \, W_{2a}'(L) + \kappa W_{2a}(L)\nonumber \\&\quad = - f_W(L) e^{-I \sigma _{i} T_1} A(T_1)^2, \nonumber \\&\qquad -GA (U_{2a}'-\theta _{2a})' - \omega _{f0}^2 \, \rho A U_{2a} \nonumber \\&\quad = - f_U' e^{I \sigma _{i} T_1} \bar{A}(T_1) B(T_1) \nonumber \\&\qquad - I \omega _{f0} \, U_{1a} \left[ 2 \, \rho A \, \frac{\mathrm{d} A}{\mathrm{d} T_1}(T_1)+ c_U A(T_1) \right] + \frac{f(Z)}{2} e^{I \sigma _{e} T_1},\nonumber \\&EJ \theta _{2a}'' + GA \, \left( U_{2a}'-\theta _{2a}\right) \nonumber \\&\qquad +\omega _{f0}^2 \, \rho J \, \theta _{2a} \nonumber \\&\quad = [f_{\theta }' + GA \, W_{1a}' \, \theta _{1a} ) ] e^{I \sigma _{i} T_1} \bar{A}(T_1) B(T_1)\nonumber \\&\qquad + I \omega _{f0} \, \theta _{1a}\left[ 2 \, \rho J \, \frac{\mathrm{d} A}{\mathrm{d} T_1}(T_1) + c_{\theta } A(T_1)\right] , \nonumber \\&U_{2a}(0)=U_{2a}(L)=\theta _{2a}'(0)=\theta _{2a}'(L)=0, \end{aligned}$$
(30)

where the functions \(f_W\), \(f_U\) and \(f_{\theta }\) are reported in “Appendix”.

4.3 Frequency response curves

The solvability conditions for the second-order problems (30) are

$$\begin{aligned}&I \omega _{a0} \, \left[ 2 \, \rho A \, r_1 \, \frac{d B}{d T_1}(T_1) + c_W \, r_1 B(T_1) \right] \nonumber \\&\quad + r_2 \, e^{-I \sigma _{i} T_1} A(T_1)^2=0, \nonumber \\&I \omega _{f0} \, \left[ 2 \, \left( \rho A \, r_3+\rho J \, r_4\right) \, \frac{\mathrm{d} A}{\mathrm{d} T_1}(T_1)\right. \nonumber \\&\quad \left. + \left( c_U \, r_3 + c_{\theta } \, r_4\right) A(T_1) \right] \nonumber \\&\quad + r_5 \, e^{I \sigma _{i} T_1} \bar{A}(T_1) B(T_1)= r_6 e^{I \sigma _{e} T_1}, \end{aligned}$$
(31)

where the parameters \(r_1,\ldots ,r_6\) are reported in “Appendix”. Note that the load is accounted for in \(r_6\). Remembering that \(x=x(\kappa _\mathrm{h},l,m)\), we observe that the other coefficients depend on l, \(\kappa _\mathrm{h}\), z (that is kept fixed in this work) and the order of transversal (n) and axial (m) natural frequencies.

As customary [34], the solution of (31) is sought after in the polar form

$$\begin{aligned} A(T_1)&=\frac{a(T_1)}{2} e^{-I \left[ \sigma _e T_1 + \beta _a(T_1)\right] }, \nonumber \\ B(T_1)&=\frac{b(T_1)}{2} e^{-I \left[ \left( 2 \sigma _e - \sigma _i\right) T_1 + \beta _b(T_1)\right] }, \end{aligned}$$
(32)

where \(a(T_1)\) and \(b(T_1)\) are real value amplitudes of the transversal and axial (first order) motions, respectively, and \(\beta _a(T_1)\) and \(\beta _b(T_1)\) are real value phase differences. In fact, rearranging (23) we obtain

$$\begin{aligned} W_1&=b(T_1) \cos [2 \Omega T + \beta _b(T_1)] W_{1a}(Z), \nonumber \\ U_1&=a(T_1) \cos [\Omega T + \beta _a(T_1)] U_{1a}(Z), \nonumber \\ \theta _{1}&=a(T_1) \cos [\Omega T + \beta _a(T_1)] \theta _{1a}(Z). \end{aligned}$$
(33)

Inserting (32) in (31) and separating real from imaginary parts, we obtain, after some algebra,

$$\begin{aligned} \frac{\mathrm{d} a}{\mathrm{d} T_1}&=-\frac{1}{2} \frac{c_U \, r_3 + c_{\theta } \, r_4 }{\rho A \, r_3 + \rho J \, r_4 } a\nonumber \\&\quad +\, \frac{r_5 \, \sin \left( 2\beta _a-\beta _b\right) }{4 \, \omega _{f0} (\rho A \, r_3 + \rho J \, r_4) } a \, b\nonumber \\&\quad -\, \frac{\sin (\beta _a)}{\omega _{f0} (\rho A \, r_3 + \rho J \, r_4)} r_6, \nonumber \\ \frac{\mathrm{d} \beta _a}{\mathrm{d} T_1}&=-\sigma _e + \frac{r_5 \, \cos (2\beta _a-\beta _b)}{4 \, \omega _{f0} \left( \rho A \, r_3 + \rho J \, r_4\right) } b\nonumber \\&\quad - \frac{\cos (\beta _a)}{\omega _{f0} \left( \rho A \, r_3 + \rho J \, r_4\right) } \frac{r_6}{a}, \nonumber \\ \frac{\mathrm{d} b}{\mathrm{d} T_1}&=-\frac{1}{2} \frac{c_W}{\rho A} b - \frac{r_2 \, \sin \left( 2\beta _a-\beta _b\right) }{4 \, \omega _{a0} \, \rho A \, r_1 } a^2, \nonumber \\ \frac{\mathrm{d} \beta _b}{\mathrm{d} T_1}&=-2 \sigma _e + \sigma _i + \frac{r_2 \, \cos \left( 2\beta _a-\beta _b\right) }{4 \, \omega _{a0} \, \rho A \, r_1} \frac{a^2}{b}. \end{aligned}$$
(34)

that are commonly known as modulation equations. Here, the dependence on \(T_1\) is omitted for brevity.

Because of (33), steady oscillations of the beam correspond to equilibrium points of (34). Setting equal to zero the derivatives in (34), we obtain an algebraic system in the four unknowns a, b, \(\beta _a\) and \(\beta _b\), that are now constant.

From the third and fourth equations, we obtain

$$\begin{aligned}&b=\frac{r_2}{2 \omega _{a0} r_1 \sqrt{4 (2\, \sigma _e-\sigma _i)^2 (\rho A)^2 + c_W^2}} a^2, \nonumber \\&\tan \left( 2 \, \beta _a - \beta _b\right) = -\frac{c_W}{2(2\sigma _e - \sigma _i) \rho A}. \end{aligned}$$
(35)

Using (35) in the first and second equations of (34), we obtain

$$\begin{aligned} \tan (\beta _a) = \frac{ 4 (c_U \, r_3 + c_{\theta } \, r_4) \omega _{f0} + \frac{r_2 \, r_5 c_W}{ \omega _{a0} r_1 \left[ 4 \left( 2\, \sigma _e-\sigma _i\right) ^2 (\rho A)^2 + c_W^2\right] } a^2 }{8 \left( \rho A \, r_3 + \rho J \, r_4\right) \sigma _e \omega _{f0} - 2 \frac{r_2 \, r_5 \rho A}{ \omega _{a0} r_1 \left[ 4 (2\, \sigma _e-\sigma _i)^2 (\rho A)^2 + c_W^2\right] } a^2}. \end{aligned}$$
(36)

and the equation

$$\begin{aligned}&\frac{r_2^2 \, r_5^2}{64 \, r_1^2 \omega _{a0}^2 \left[ 4 (2\, \sigma _e-\sigma _i)^2 (\rho A)^2 + c_W^2\right] } a^6 \nonumber \\&\quad -\frac{r_2 \, r_5 \, \omega _{f0} \left[ 4 \rho A \, \sigma _e \left( 2 \sigma _e - \sigma _i\right) \left( \rho A \, r_3 + \rho J \, r_4\right) -c_W \left( c_U \, r_3 + c_{\theta } \, r_4\right) \right] }{8 \, r_1 \omega _{a0} [4 (2\, \sigma _e-\sigma _i)^2 (\rho A)^2 + c_W^2]} a^4 \nonumber \\&\quad + \frac{\omega _{f0}^2 \left[ 4 \, \sigma _e^2 \left( \rho A \, r_3 + \rho J \, r_4\right) ^2 + \left( c_U \, r_3 + c_{\theta } \, r_4\right) ^2 \right] }{4} a^2=r_6^2, \end{aligned}$$
(37)

which is third order in the unknown \(y=a^2\), so that its closed form solution is known. Once \(a(l,\kappa _\mathrm{h},n,m,c_W,c_U,c_{\theta },r_6,\Omega )\) has been determined, b, \(\beta _a\) and \(\beta _b\) can be computed from (35) and (36). When all parameters are fixed, and only the external excitation \(\Omega \) is varied, the searched frequency response curves (FRCs) are obtained.

Equation (37) is cubic in \(a^2\). Thus, there always exists a real solution. Furthermore, it may happen that three real solutions exist. This occurs in particular in the neighbourhood of resonance, as we will see in the following.

In the very special case of perfect internal (\(\sigma _i=0\)) and external (\(\sigma _e=0\)) resonances, i.e. \(\omega _{a0}=2 \omega _{f0}=2 \Omega \), Eq. (37) reduces to

$$\begin{aligned}&a \left| \frac{1}{16} \frac{r_2 \, r_5 \, a^2}{r_1 c_W \omega _{f0}} + \frac{1}{2} \omega _{f0} (c_U \, r_3 + c_{\theta } r_4) \right| = |r_6|. \end{aligned}$$
(38)

In this case, the asymptotic development of the solution with respect to \(c_W\) is given by

$$\begin{aligned} a =&\root 3 \of {\frac{16 \, r_1 \, r_6 \, \omega _{f0}}{r_2 \, r_5}} \root 3 \of {c_W} + \cdots , \nonumber \\ b =&\root 3 \of {\frac{4 \, r_2 \, r_6^2}{r_1 \, r_5^2 \, \omega _{f0}}} \, \frac{1}{c_W}+ \cdots , \end{aligned}$$
(39)

which shows that for \(c_W\rightarrow 0\) we have \(b \rightarrow \infty \). This highlights the role played by \(c_W\) in the resonance.

The stability of the solutions previously obtained can be determined by computing the eigenvalues of the Jacobian of the right-hand side of (34) at each equilibrium point. If all the four eigenvalues have negative real part, the solution is stable; otherwise, it is unstable. In particular, if there is a real positive eigenvalue, the solution is a saddle, while if there is a complex eigenvalue with positive real part, the solution is a source.

By varying the parameters, if a real eigenvalue passes from negative to positive, we have a saddle–node bifurcation, while if a complex eigenvalue passes from negative real part to positive, we have a Neimark–Sacker, or secondary Hopf, bifurcation, and a quasi-periodic solution is born in the mechanical system. Because of their geometrical properties, saddle–node bifurcations can be detected by looking for the zeros of the discriminant of Eq. (37), where we pass from 1 to 3 real solutions.

4.4 Backbone curves

In the absence of excitation, \(r_6=0\), and damping, \(c_W=c_U=c_{\theta }=0\), the beam undergoes a free motion, of frequency \(\Omega \) (see 33). In this case, (37) simplifies to

$$\begin{aligned}&\frac{r_2^2 \, r_5^2}{256 \, r_1^2 \omega _{a0}^2 \, \left( 2\, \sigma _e-\sigma _i\right) ^2 (\rho A)^2} a^6\nonumber \\&\quad -\frac{r_2 \, r_5 \, \omega _{f0} \, \sigma _e \left( \rho A \, r_3 + \rho J \, r_4\right) }{8 \, r_1 \omega _{a0} (2\, \sigma _e-\sigma _i) \rho A} a^4 \nonumber \\&\quad +\omega _{f0}^2 \, \sigma _e^2 (\rho A \, r_3 + \rho J \, r_4)^2 a^2=0, \end{aligned}$$
(40)

which can be rewritten as

$$\begin{aligned}&a^2 \left( \frac{r_2 \, r_5}{16 \, r_1 \, \omega _{a0} \, \left( 2\, \sigma _e-\sigma _i\right) \rho A} a^2\right. \nonumber \\&\left. \quad - \omega _{f0} \, \sigma _e \left( \rho A \, r_3 + \rho J \, r_4\right) \right) ^2=0. \end{aligned}$$
(41)

Thus, excluding the trivial solution \(a=0\), we have

$$\begin{aligned} a^2 =16 \frac{r_1 \, \rho A \, \left( \rho A \, r_3 + \rho J r_4\right) }{r_2 \, r_5} \omega _{a0} \, \omega _{f0} \sigma _e \left( 2\, \sigma _e-\sigma _i\right) , \end{aligned}$$
(42)

and then (the sign function is \(\text {sign}(y)=y/|y|\))

$$\begin{aligned} b= 4 \frac{ \rho A \, r_3 + \rho J \, r_4}{r_5} \, \omega _{f0} \, \sigma _e \, \text {sign}\left( 2\, \sigma _e-\sigma _i\right) . \end{aligned}$$
(43)

They represent the analytical expressions for the so-called BackBone Curves (BBCs) of coupled oscillators, which give the amplitudes of the oscillation as a function of the vibration frequency \(\Omega \). As it happens for the BBCs of uncoupled oscillators [34], they are also the loci of maximum points of frequency response curves, as we will see in the next section.

When all parameters but \(\Omega \) are fixed, only \(\sigma _e\) is varying in (42) and (43), so that \(a(\sigma _e) \sim \sqrt{ \sigma _e (2\, \sigma _e-\sigma _i)}\) and \(b(\sigma _e) \sim \sigma _e \, \text {sign}(2\, \sigma _e-\sigma _i)\), this being a property that helps to understand the behaviour of the BBCs. In particular, we note that \(a(\sigma _e)\) exists only when \(\sigma _e \notin [\min \{0,\sigma _i/2\};\max \{0,\sigma _i/2\}]\), and locally it behaves like a square root. \(b(\sigma _e)\) exists in the same range, where it is (piecewise) linear.

In the very special case of perfect resonance, \(\sigma _i=0\) and \(\omega _{a0}=2\omega _{f0}\), the previous expressions simplify to

$$\begin{aligned} a&= 8 \sqrt{\frac{r_1 \, \rho A \, (\rho A \, r_3 + \rho J r_4)}{r_2 \, r_5}} \omega _{f0} \, |\sigma _e|, \nonumber \\ b&= 8 \frac{ (\rho A \, r_3 + \rho J \, r_4)}{r_5} \, \omega _{f0} |\sigma _e|, \end{aligned}$$
(44)

and both curves become proportional to \(|\sigma _e|\) (see forthcoming Fig. 9d).

5 Results

Although the analysis of the solution can be done in dimensionless form, to refer to a real case and to compare the results with those obtained by numerical simulations, we prefer to deal with a dimensional case.

We choose a beam of \(0.05\times 0.05\) m\(^2\) square cross section, made of steel (\(E=2.1\times 10^{11}\) N/m\(^2\), \(\rho =7850\) kg/m\(^3\), \(\nu =0.3\)), of length \(L=0.5\) m. We then have \(l=10 \, \sqrt{2}=34.6410\) and \(z=0.3287\), so that we are exactly in the case of Fig. 4. We also have \(\omega _{f0}=11089.77\) rad/s (the period is \(5.66\times 10^{-4}\) sec) and \(\omega _{a0}=10344.39 \,x\) rad/s. For this case, the perfect 1 : 2 internal resonance between the second transversal mode (\(n=2\)) and the first axial mode (\(m=1\)) is obtained at \(\kappa _{h,ir}=1661.24\), see point “D” in Fig. 6b. We will vary \(\kappa _\mathrm{h}\) around this value.

Fig. 7
figure 7

Frequency response curves for \(\kappa _\mathrm{h}=1620\) and for \(Q=300\) (bottom curve); 600; 800; 1000; 1200 (top curve) N. Continuous black lines are stable solution branches, red dashed lines are unstable saddle-type solution branches, blue dashed lines are unstable source-type solution branches. Green dashdot lines are the backbone curves. (Colours in the online version)

Full size image

We further assume \(C_W=C_U=50\) N sec/m\(^2\) and \(C_{\theta }=1.5\) N sec. The load is a concentrated force Q applied at L/4 (in order to excite the second transversal mode), so that \(r_6=Q \, \sin (n\, \pi /4)/2=Q/2\) N (since \(n=2\)). Any other distribution of load providing the same \(r_6\) is equivalent to the present one. For comparison with the forthcoming dynamical case, we note that the transversal static displacement in the point where the force is applied is, within the small displacements linear theory, \(U(L/4)=(3/256)(Q\, L^3 /EJ) = 0.0134\) mm for \(Q=1000\) N.

The FRCs \(U_{\max }(L/4) = a(\Omega ) \, U_{1a}(L/4)\) and \(W_{\max }(L/4) = b(\Omega ) \, W_{1a}(L/4)\), and the related BBCs are obtained by varying the external frequency \(\Omega \) around \(\omega _{f0}\). Here, “\(\max \)” means maximum in time, and only the first-order terms (33) are considered.

5.1 The effect of the excitation amplitude

We start with by considering the effect of the excitation amplitude Q for the fixed value \(\kappa _\mathrm{h}=1620\). Here, we have

$$\begin{aligned} r_1&=0.3029 \text { m}, \quad r_2=1.6007 \times 10^{10} \text { N/m}^2, \quad r_3=0.25 \text { m}, \nonumber \\ r_4&=32.7957 \text { m}^{-1}, \quad r_5=3.1115 \times 10^{10} \text { N/m}^2, \end{aligned}$$
(45)

and

$$\begin{aligned} \omega _{a0}=22082.20 \text { rad/s}, \quad \kappa =1.4175 \times 10^9 \text { N/m}. \end{aligned}$$
(46)

Note that, according to (14) and (15), \(\omega _{a0}\) depends on \(\kappa _\mathrm{h}\), and thus, it slightly varies when \(\kappa _\mathrm{h}\) varies from the value 1620. The FRCs and the BBCs are reported in Fig. 7, which shows how the excitation amplitude increases the amplitude of the response, as expected, but not in a linear way. The dynamic transversal displacement in correspondence of the peak is about 100 times larger than the static one.

The stability of each branch is determined as illustrated at the end of Sect. 4.3. For example, for \(Q=1000\) N and \(\Omega =11120\) rad/s we have the following equilibrium points and associated eigevalues:

$$\begin{aligned} a_1&=0.8685 \, \text {mm} \quad \text {(stable)}: \nonumber \\ \mu _{1,2}=&-3.2191 \pm 116.5082 I; \nonumber \\ \mu _{3,4}&=-4.1747 \pm 10.9506 I; \nonumber \\ a_2&=0.7832 \, \text {mm}\quad \text {(unstable)}: \nonumber \\ \mu _{1,2}&=-3.5693 \pm 115.6535 I; \nonumber \\ \mu _3&=7.4617; \,\, \mu _4=-15.1108; \nonumber \\ a_3&=0.1309 \, \text {mm} \quad \text {(stable)}: \nonumber \\ \mu _{1,2}&=-1.8670 \pm 37.7398 I; \nonumber \\ \mu _{3,4}&=-5.5268 \pm 74.2153 I. \end{aligned}$$
(47)

Overall there are two unstable solution branches of saddle-type (reported in red), that are bounded by two saddle–node (SN) bifurcations each, and an unstable solution branch, of source-type (reported in blue), that is bounded by two Neimark–Sacker (NS) bifurcations, that are seen in Fig. 7. For \(Q=1000\) N, the maximum real part of the eigenvalues is reported in Fig. 8 for each branch, from which we clearly see the stable \((\max \mathrm{Re}(\lambda )<0)\) and the unstable \((\max \mathrm{Re}(\lambda )>0)\) solution branches. The bifurcation points are where these curves cross the abscissa axes \(((\max \mathrm{Re}(\lambda )=0))\), that happens for

$$\begin{aligned} \Omega _{SN1}&=11006.2178 \, \text {rad/s}, \nonumber \\ \Omega _{SN2}&=11034.6418 \, \text {rad/s}, \nonumber \\ \Omega _{NS1}&=11034.9573 \, \text {rad/s}, \nonumber \\ \Omega _{NS2}&=11041.0995 \, \text {rad/s}, \nonumber \\ \Omega _{SN3}&=11113.6530 \, \text {rad/s}, \nonumber \\ \Omega _{SN4}&=11134.2210 \, \text {rad/s}. \end{aligned}$$
(48)

The source-type unstable solution branch is quite narrow. For low values of the load (\(Q=300\) N), there is a unique stable solution branch, having peaks in correspondence of the resonances.

Fig. 8
figure 8

The maximum real part of the eigenvalues for \(\kappa _\mathrm{h}=1620\) and \(Q=1000\) N. Continuous black lines are stable solution branches, red dashed lines are unstable saddle-type solution branches, blue dashed lines are unstable source-type solution branches. (Colours in the online version)

Full size image

5.2 The transition from hardening to softening

The transition from hardening to softening is illustrated in Fig. 9 to show what really happens through the (apparent) singularity of Fig. 4. For \(\kappa _\mathrm{h}\) quite below \(\kappa _{h,ir}\) (Fig. 9a), we are far from the internal resonance. In correspondence of \(\omega _{a0}/2\), there is no amplification on U, because the excitation is not in primary resonance with the transversal mode, while we have a classical resonance curve in W, which is practically vertical. Here, the resonance mechanism is the following: (1) the external excitation induces small vibration on the transversal displacement; (2) the weak nonlinear coupling from U to W, illustrated in [8], induces small oscillations on the axial displacement; (3) since the external excitation is just in order-2 superharmonic resonance with the axial mode, there is a resonance amplification, linear because the transversal mode transfers only a small amount of energy to the axial one. In turn, around \(\omega _{f0}\), the FRC of U is hardening (in agreement with \(\omega _2>0\) in Fig. 4), and that of W behaves similarly, due again to the mere nonlinear coupling away from internal resonance [8]. Note that the transversal displacement (directly excited) is about 15 times larger than the axial one.

Fig. 9
figure 9

Frequency response curves for \(Q=1000\) N and different values of \(\kappa _\mathrm{h}\). Continuous black lines are stable solution branches, red dashed lines are unstable saddle-type solution branches, blue dashed lines are unstable source-type solution branches. Green dashdot lines are the backbone curves. (Colours in the online version)

Full size image

Increasing \(\kappa _\mathrm{h}\) (Fig. 9b), the major change is that a softening resonance curve is observed in both W and U around \(\omega _{a0}/2\). The meaningful nonlinear effect of the internal resonance is apparent in the left peaks, the W one being much more important than the corresponding hardening peak around \(\omega _{f0}\) which represents the nearly unchanged effect from U to W due to the nonlinear coupling. Note also the clearly visible piecewise linear behaviour of the BBCs of b in Fig. 9b2.

Fig. 10
figure 10

Frequency response curves for \(Q=1000\) N and different values of \(\kappa _\mathrm{h}\). Continuous black lines are stable solution branches, red dashed lines are unstable saddle-type solution branches, blue dashed lines are unstable source-type solution branches. Green dashdot line is the backbone curve ensuing from \(\omega _{a0}/2\). (Colours in the online version)

Full size image

By further increasing \(\kappa _\mathrm{h}\) (Fig. 9c), thus getting closer to the exact internal resonance, the softening FRC around \(\omega _{a0}/2\) becomes more important, both in terms of U and W. In W, a third peak appears exactly at \(\omega _{a0}/2\), suggesting a further second-order coupling-induced effect from U to W; however, this peak belongs to the unstable solution branch. The hardening branch of the FRC around \(\omega _{f0}\) is still practically unchanged.

For \(\kappa _\mathrm{h}=1660\) (Fig. 9d), i.e. practically in the perfect resonance, the left softening and the right hardening cusps become symmetrical with respect to the line \(\Omega =\omega _{f0}=\omega _{a0}/2\), and thus, they reach the same importance. The third, unstable, W-peak is clearly evident in Fig. 9d2. Here, the coupling due to the internal resonance is maximum, and the two BBCs, one hardening and one softening, ensue from \(\omega _{f0}\), and are piecewise linear, as found in (44).

The increment of \(\kappa _\mathrm{h}\) (Fig. 9e) implies that the FRC branch associated with \(\omega _{f0}\) becomes the left one, which is softening, while its hardening branch (associated with \(\omega _{a0}/2\)) becomes slightly less important in terms of U, but more important in terms of W. Indeed, note that Fig. 9e is “specular” to Fig. 9c. This trend is confirmed by Fig. 9f, which is “specular” to Fig. 9d, and by Fig. 9g, which is “specular” to Fig. 9a.

The conclusion is that, taking properly into account the internal resonance, there is no singularity in the hardening to softening transition by varying \(\kappa _\mathrm{h}\). There is, instead, a sudden (discontinuous) jump, of finite magnitude, from hardening to softening, and in the discontinuity point \(\kappa _{h,ir}\), where exact internal resonance occurs, the BBCs are linear instead of proportional to a square root.

Finally, we report in Fig. 9h the behaviour for much larger values of \(\kappa _\mathrm{h}\), away from internal resonance, to show how the softening behaviour decreases (the U curve becomes almost vertical, and thus, the nonlinear correction coefficient almost zero). This is in agreement with the behaviour illustrated in Fig. 4, and it is somehow surprising, since the present analysis is expected to be reliable only in a rather strict neighbourhood of \(\kappa _{h,ir}\).

5.3 An isolated branch of solution

The born of the left resonance curve (see Fig. 9b) is actually more involved than expected, and interesting. An isolated branch of solution, also termed as “isola”, is born at about \(\kappa _{h}=1580\) (Fig. 10a, b). By increasing \(\kappa _{h}\), this closed branch enlarges (Fig. 10c, d) and finally touches, at about \(\kappa _{h}=1591.5\) (Fig. 10d, e), the non-resonant, small amplitude, branch. Then, a classical resonant (softening) FRC is observed (Fig. 10f). The same phenomenon has been observed, for example, in [35] (see their Fig. 6) and in [36] (see their Fig. 2).

It is just for isolated branches that analytical methods, even approximate, are necessary: here multiple time scales are used, but in other papers (e.g., [37]) isolas have been detected by the harmonic balance method. In fact, they cannot be obtained by a path following algorithm starting from the main solution branch unless varying another parameter (for example, the stiffness of the spring), besides the excitation frequency, which may allow to reach isolas in an extended parameter space. If varying only the excitation frequency, they can be found numerically only via a suitable and lucky choice of initial values in either the original governing equations or the reduced (e.g., modulated) ones, and then possibly characterized systematically by building basins of attraction, which is however difficult and demanding, especially for high dimensional systems.

Detecting stable isolated solutions is not only important from a theoretical point of view. In fact, even if these attractors may have a small basin of attraction, and thus be considered “minor” or “rare”, it may happen that their basins strongly erode, by fractality, the basin of the main attractor (the one used in applications), that thus loses robustness and reduces its safety, leading to instability for moderately large perturbations, even if the attractor is stable in the Lyapunov sense [38].

6 Numerical simulations

To confirm the previous analytical findings, finite elements method (FEM) simulations are performed. The same beam illustrated in Sect. 5 is considered.

The commercial software Abaqus_CAE \(\copyright \) is used. The beam is discretized using 100 B21-type elements. An explicit direct time integration is used, with time step \(\Delta T= (2 \pi )/(\Omega \times 80) \) sec and, to give up the transient vibration, each excitation lasts 2500 periods. Furthermore, in the solver a double precision is used together with full nodal output precision.

Relatively small changes in \(\Omega \) (1 rad/s) are used in the frequency sweeping (both forward and backward), and the solution (shape deformation and rotation angle) obtained in the previous step is used as initial condition, as done in [11].

Axial and transversal dampings proportional to the mass matrices are considered, with the same values of the damping coefficients used in Sect. 5.

To further confirm our results, we have done computations also with another commercial software, Midas_GEN \(\copyright \), but since the outcomes are comparable we do not report these simulations.

First, the axial and transversal natural frequencies have been computed in the linear regime, verifying that they perfectly match those computed analytically. Then, the FRCs have been obtained in the geometrically nonlinear regime, i.e. with large displacements. Since a brute force following algorithm has been used to determine the numerical FRC, for increasing and decreasing frequencies, only the stable branches have been detected. To draw also the unstable branches, a continuation algorithm should have been used, which is, however, out of the scope of the present work.

The comparison between analytical and numerical results is reported in Fig. 11, for a fixed value of \(\kappa \) and for increasing values of Q. We conclude that an excellent agreement is obtained on the main (i.e. primary resonance) stable solution branches. Surprisingly, the peaks of the numerical curves are higher than those of the analytical ones, this being likely due to a different fine tuning of the damping, that has large effects on the peak value. Note that no tuning of damping is done, and the nominal values are considered in numerical and analytical simulations.

Around \(\omega _{a0}/2\), we observe that the numerical solution is not able to catch the upper, resonant, stable branch. This is due to the source-type unstable solution branch that breaks the main resonant solution branch and leads to a jump of the theoretical solution. The numerical jump is not observed, likely because the solutions have very small basins of attraction.

Fig. 11
figure 11

Comparison of numerical (circles) and analytical (continuous lines) FRCs for \(\kappa _\mathrm{h}=1620\) (\(\kappa =1.4175 \times 10^9\) N/m). In this case, \(\omega _{a0}/2=11041.10\) rad/s is slightly lesser than \(\omega _{f0}=11089.77\) rad/s. a, b \(Q=800\) N; c, d \(Q=1000\) N; e, f \(Q=1200\) N

Full size image

Keeping \(Q=1000\) N fixed, and varying the spring stiffness, the comparison between analytical and numerical results is reported in Fig. 12. In addition to the overall excellent agreement, with some minor quantitative differences on W (which can be reduced by tuning the damping), the most important result is that through the Neimark–Sacker bifurcation a quasi-periodic attractor is born, according to what the theory predicts for this event [39]. It is highlighted by the cloud of points obtained for each frequency by sampling the maximum amplitudes of the last 500 periods of the excitation, to give rid of the transient behaviour.

This is a further confirmation of the reliability of the proposed analysis.

Fig. 12
figure 12

Comparison of numerical (circles) and analytical (continuous lines) FRCs for \(Q=1000\) N. a, b \(\kappa _\mathrm{h}=1650.7\) (\(\kappa =1.4444 \times 10^9\) N/m), so that \(\omega _{a0}/2=11077.46\) rad/s and \(\omega _{f0}=11089.77\) rad/s; c, d \(\kappa _\mathrm{h}=1659.4\) (\(\kappa =1.4520 \times 10^9\) N/m), so that \(\omega _{a0}/2=11087.65\) rad/s and \(\omega _{f0}=11089.77\) rad/s, namely we are practically in exact internal resonance

Full size image

7 Conclusions and further developments

The internal resonance between axial and bending modes in a Timoshenko beam with a boundary axial spring has been investigated, with the aim (1) of studying the ensuing modal interaction in a further mechanical system, (2) of explaining a singular behaviour previously reported in the literature, and (3) of investigating the transition from softening to hardening through the 1 : 2 internal resonance by varying the axial spring stiffness.

It has been shown that internal resonance, while structurally unstable, is a robust phenomenon, since it occurs for all values of the end stiffness, and for “any” value of the resonance ratio ir. It is only needed to properly select the beam length.

Attention has then been paid to the nonlinear behaviour around the 1 : 2 internal resonance. The frequency response curves, and the associated backbone curves, have been obtained analytically by the multiple time scales method. It has been shown that, by varying the spring stiffness across the resonance value, the frequency response curves of the internally resonant axial and transversal modes intersect and exchange with each other, leading to an instantaneous, but not singular, jump from hardening to softening of the flexural mode, thus explaining an apparent singularity previously reported when internal resonance is not taken into account.

A detaching of an isolated solution branch from the frequency response curves, similar to others previously reported in the literature, has been observed, too.

Finally, the analytical frequency response curves have been compared with their counterparts obtained by finite element numerical simulations. Overall, a very good agreement has been observed for the considered values of the parameters.

As far as further developments are concerned, at least the following ones can be mentioned:

  • To explain possible singular behaviour of higher order nonlinear correction coefficient \(\omega _4\) in terms of 1:4 internal resonance;

  • To study other internal resonances, including a combination one, between axial and transversal modes, both in linear and nonlinear regimes;

  • To consider different boundary conditions;

  • To exploit the investigated internal resonance for practical purposes (e.g. energy harvesting) and engineering design;

  • To perform experimental investigations tailored around internal resonance;

  • To demonstrate that the coupled backbones tend to their uncoupled counterparts when getting far from the resonance.