On the frequency response computation of geometrically nonlinear flat structures using reduced-order finite element models

Abstract

This paper presents a general methodology to compute nonlinear frequency responses of flat structures subjected to large amplitude transverse vibrations, within a finite element context. A reduced-order model (ROM) is obtained by an expansion onto the eigenmode basis of the associated linearized problem, including transverse and in-plane modes. The coefficients of the nonlinear terms of the ROM are computed thanks to a non-intrusive method, using any existing nonlinear finite element code. The direct comparison to analytical models of beams and plates proves that a lot of coefficients can be neglected and that the in-plane motion can be condensed to the transverse motion, thus giving generic rules to simplify the ROM. Then, a continuation technique, based on an asymptotic numerical method and the harmonic balance method, is used to compute the frequency response in free (nonlinear mode computation) or harmonically forced vibrations. The whole procedure is tested on a straight beam, a clamped circular plate and a free perforated plate for which some nonlinear modes are computed, including internal resonances. The convergence with harmonic numbers and oscillators is investigated. It shows that keeping a few of them is sufficient in a range of displacements corresponding to the order of the structure’s thickness, with a complexity of the simulated nonlinear phenomena that increase very fast with the number of harmonics and oscillators.

Appendices

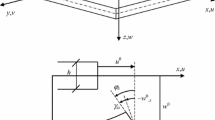
Appendix A: The beam (u,w) model

The beam model of Eq. (1) is here discussed. Using Hamilton principle, one obtained the classical equations of motion for the axial and transverse motion of the beam, which are:

$$\begin{aligned} \rho S \ddot{w} + EIw_{,xxxx} - \left( N w_{,x}\right) _{,x}&= p(x,t) \end{aligned}$$

(44a)

$$\begin{aligned} \rho S \ddot{u} - N_{,x}&= n(x,t). \end{aligned}$$

(44b)

where p(x, t) and n(x, t) are distributed transverse and in-plane forces per unit length and where the axial force in the beam is:

$$\begin{aligned} N=ES\left( u_{,x} + \frac{1}{2} w_{,x}^2\right) . \end{aligned}$$

(45)

Equations (45) and (44a, b) constitute the classical von Kármán model describing the transverse motion of a beam with geometrical nonlinearities [12, 15, 16]. Then, eliminating N between Eqs. (45) and (44a, b) leads to the (u, w) model of Eq. (1).

After the modal expansion of Sect. 2.1, the analytical expressions of the coefficients of nonlinear terms in Eq. (7a, b) are:

$$\begin{aligned} C_{pi}^k= & {} -\frac{\displaystyle {\int _0^1 (\varPsi _{p,x} \varPhi _{i,x})_{,x} \varPhi _{k} \,\text {d}x}}{\displaystyle {\int _0^1 \varPhi _k^2 \,\text {d}x}}, \nonumber \\ G_{ij}^p= & {} \frac{\displaystyle { \int _0^1 \varPsi _{p} \varPhi _{i,x} \varPhi _{j,xx} \,\text {d}x}}{\displaystyle { \int _0^1 \varPsi _p^2 \,\text {d}x}} \end{aligned}$$

(46a)

$$\begin{aligned} D_{ijl}^k= & {} - \frac{1}{2} \frac{\displaystyle { \int _0^1 (\varPhi _{i,x} \varPhi _{j,x} \varPhi _{l,x})_{,x} \varPhi _k\,\text {d}x}}{\displaystyle { \int _0^1 \varPhi _k^2 \,\text {d}x}}, \end{aligned}$$

(46b)

$$\begin{aligned} Q_k(t)= & {} \frac{\displaystyle { \int _0^1 \varPhi _k(x)p(x,t)\,\text {d}x}}{\displaystyle { \int _0^1 \varPhi _k^2 \text {d}x}},\nonumber \\ E_p(t)= & {} \frac{\displaystyle { \int _0^1 \varPsi _p(x)n(x,t)\,\text {d}x}}{\displaystyle { \int _0^1 \varPsi _p^2 \text {d}x}}. \end{aligned}$$

(46c)

The modes are here normalized as:

$$\begin{aligned} \int _0^1\varPhi _k^2(x)\,\text {d}x=\int _0^1\varPsi _p^2(x)\,\text {d}x=1. \end{aligned}$$

(47)

Table 9 Numerical values, computed with a trapezoidal rule, of some nonlinear coefficients of a the clamped–clamped beam model (Eqs. (46a, b)). Scaling of Eqs. (2) and mode normalization of Eqs. (47)

In the case of a clamped–clamped boundary conditions, the transverse mode shapes are solution of Eq. (6a) and can be written:

$$\begin{aligned} \varPhi _k(x)= & {} \kappa _k\left[ (\sin \beta _k-\sinh \beta _k)(\cos \beta _kx- \cosh \beta _kx)\right. \nonumber \\&\left. -(\cos \beta _k-\cosh \beta _k)(\sin \beta _kx-\sinh \beta _kx)\right] .\nonumber \\ \end{aligned}$$

(48)

with $\cos \beta _k\cosh \beta _k-1=0,\quad \omega _k=\beta _k^2$ for all $k>1$ and $\kappa _k$ is numerically computed to verify Eq. (47). The axial mode shapes are solutions of Eq. (6b) and can be written:

$$\begin{aligned} \varPsi _p(x)=\sqrt{2}\sin \gamma _px,\quad \gamma _p=p\pi . \end{aligned}$$

(49)

They naturally verify Eq. (47). The values of some of these coefficients are given in Table 9.

Appendix B: On the plate $(\varvec{u},w)$-formulation ROM

Some details about the analytical plate model of Sect. 2.2 are given here. The in-plane forces in the plate are represented by a two-dimensional tensor $\varvec{N}$, which, with the von Kármán assumptions, can be written [14]:

$$\begin{aligned} \varvec{N}= & {} A\left[ (1-\nu )\varvec{\epsilon }+\nu {\text {tr}}\varvec{\epsilon }\varvec{1}\right] ,\nonumber \\ \varvec{\epsilon }= & {} \frac{1}{2}\left( \varvec{\nabla }\varvec{u}+\varvec{\nabla }^{{\text {T}}}\varvec{u} + \varvec{\nabla }w\otimes \varvec{\nabla }w\right) \end{aligned}$$

(50)

where $\varvec{\epsilon }$ is the in-plane strain tensor, $A=Eh/(1-\nu ^2)$ is the in-plane stiffness of the plate, $\varvec{\nabla }$ denotes the vector/tensor gradients of scalar/vector fields, ${\text {tr}}$ is the trace of a tensor $\otimes$ is the tensor product of two vectors and $\varvec{1}$ is the identity tensor.

By eliminating $\varvec{N}$ between Eqs. (50) and (11a, b), one obtains the following $(\varvec{u},w)$-formulation:

$$\begin{aligned}&\rho h \ddot{w}+ D \Delta \Delta w {-} A \Big [ (1{-}\nu )\Big (\varvec{\nabla }\varvec{u}:\varvec{\nabla }\varvec{\nabla }w + \varvec{\Delta }\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad +\nu \Big ({\mathrm{div}}\,\varvec{u} \,\Delta w + \varvec{\nabla }{\mathrm{div}}\,\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad + \varvec{\nabla }w \cdot \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w + \frac{1}{2} (\varvec{\nabla }w)^2 \,\Delta w\Big ] = 0. \end{aligned}$$

(51a)

$$\begin{aligned}&\rho h \ddot{\varvec{u}} - \frac{A}{2}\Big [ (1-\nu ) \varvec{\Delta }\varvec{u} + (1+\nu ) \varvec{\nabla }{\mathrm{div}}\,\varvec{u} \nonumber \\&\quad +(1-\nu ) \Delta w \varvec{\nabla }w + (1+\nu ) \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w \Big ] = 0. \end{aligned}$$

(51b)

where  :  denotes the doubly contracted product of two tensors, $\varvec{\Delta }$ the vector Laplacian of a vector field and $\cdot$ the dot product.

With the following dimensionless variables:

$$\begin{aligned} {\bar{w}}= & {} \frac{w}{h} , \quad \bar{\varvec{r}} = \frac{\varvec{r}}{L} \quad {\bar{F}}=\frac{F}{Eh^3}, \nonumber \\ \varepsilon= & {} 12(1-\nu ^2),\quad {\bar{t}}=\frac{1}{L^2}\sqrt{\frac{D}{\rho h}}t,\quad {\bar{p}}= \frac{L^4}{Dh} p, \end{aligned}$$

(52)

$$\begin{aligned} {\tilde{\varepsilon }}= & {} \frac{Ah^2}{D}=\frac{\varepsilon }{1-\nu ^2}=12,\quad \mu = \frac{D}{AL^2},\nonumber \\ \bar{\varvec{u}}= & {} \frac{L}{h^2}\varvec{u},\quad \bar{\varvec{N}}=\frac{L^2}{Eh^3}\varvec{N}. \end{aligned}$$

(53)

where L is a characteristic dimension of the middle plane of the plate (its diameter for instance). The $(\varvec{u},w)$-formulation is then rewritten:

$$\begin{aligned}&\ddot{w} + \Delta \Delta w - {\tilde{\varepsilon }}\Big [ (1-\nu )\Big (\varvec{\nabla }\varvec{u}:\varvec{\nabla }\varvec{\nabla }w + \varvec{\Delta }\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad +\nu \Big ({\mathrm{div}}\,\varvec{u} \,\Delta w + \varvec{\nabla }{\mathrm{div}}\,\varvec{u}\cdot \varvec{\nabla }w\Big ) \nonumber \\&\quad + \varvec{\nabla }w \cdot \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w + \frac{1}{2} (\varvec{\nabla }w)^2 \,\Delta w\Big ] = 0. \end{aligned}$$

(54a)

$$\begin{aligned}&\mu \ddot{\varvec{u}} - \Big [ (1-\nu ) \varvec{\Delta }\varvec{u} + (1+\nu ) \varvec{\nabla }{\mathrm{div}}\,\varvec{u} \nonumber \\&\quad +(1-\nu ) \Delta w \varvec{\nabla }w + (1+\nu ) \varvec{\nabla }\varvec{\nabla }w \cdot \varvec{\nabla }w \Big ] = 0. \end{aligned}$$

(54b)

The bending and in-plane displacements are expanded onto a linear basis of, respectively, $N_w$ transverse modes $\varPhi _k$ and $N_u$ axial modes $\varvec{\varPsi }_p$:

$$\begin{aligned}&w(\varvec{r},t) = \sum _{k=1}^{N_w} \varPhi _k(\varvec{r}) q_k(t) \quad \text {and} \nonumber \\&\quad \varvec{u}(\varvec{r},t) = \sum _{p=N_w+1}^{N_u+N_w} \varvec{\varPsi }_p(x) \eta _p(t). \end{aligned}$$

(55)

The modes are chosen to satisfy the following two eigenproblems associated with the linear parts of Eqs. (54a, b):

$$\begin{aligned}&\Delta \Delta \varPhi _{k} - \omega ^2_k \varPhi _k = 0 \end{aligned}$$

(56a)

$$\begin{aligned}&(1-\nu )\varvec{\Delta }\varvec{\varPsi }_{p} + (1+\nu )\varvec{\nabla }{\mathrm{div}}\,\varvec{\varPsi }_{p} - \gamma _p^2 \varPsi _p = 0 \end{aligned}$$

(56b)

Table 10 Numerical values of the cubic coefficients $\varGamma _{ijl}^k$ of Eq. (9), for the clamped–clamped beam [(u, w)-formulation, Eq. (10), scaling of Eq. (2) and mode normalization of Eq. (47)] and the clamped circular plate [(w, F)-formulation of section C, Eq. (63), scaling of Eqs. (52) and mode normalization of Eqs. (65)]

where $\omega _k$ and $\gamma _p$ are the transverse and in-plane dimensionless eigenfrequencies (the frequency equation of the in-plane vibrations of a clamped circular plate has been derived in [69]). Then, by multiplying (54a, b), respectively, by $\varPhi _k$ and $\varvec{\varPsi }_p$, integrating on the mid-plane surface ${\mathcal {S}}$ and using the orthogonality properties, the ROM of Eqs. (7a, b) is obtained, with:

$$\begin{aligned} C_{pi}^k= & {} -\frac{\displaystyle {\int _{\mathcal {S}} \Big [(1-\nu )\Big (\varvec{\nabla }\varvec{\varPsi }_p:\varvec{\nabla }\varvec{\nabla }\varPhi _i + \varvec{\Delta }\varvec{\varPsi }_p\cdot \varvec{\nabla }\varPhi _i\Big )+\nu \Big ({\mathrm{div}}\,\varvec{\varPsi }_p \,\Delta \varPhi _i + \varvec{\nabla }{\mathrm{div}}\,\varvec{\varPsi }_p\cdot \varvec{\nabla }\varPhi _i\Big )\Big ]\varPhi _k\,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}, \end{aligned}$$

(57a)

$$\begin{aligned} G_{ij}^p= & {} \frac{\displaystyle {\int _{\mathcal {S}} \Big [(1-\nu ) \Delta \varPhi _i \varvec{\nabla }\varPhi _j + (1+\nu ) \varvec{\nabla }\varvec{\nabla }\varPhi _i \cdot \varvec{\nabla }\varPhi _j \Big ]\cdot \varvec{\varPsi }_p \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varvec{\varPsi }_p^2 \,\text {d}S}},\nonumber \\ \end{aligned}$$

(57b)

$$\begin{aligned} D_{ijl}^k= & {} - \frac{\displaystyle {\int _{\mathcal {S}} \Big [\varvec{\nabla }\varPhi _i \cdot \varvec{\nabla }\varvec{\nabla }\varPhi _j \cdot \varvec{\nabla }\varPhi _l + \frac{1}{2} \varvec{\nabla }\varPhi _i\cdot \varvec{\nabla }\varPhi _j \,\Delta \varPhi _l\Big ]\varPhi _k \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}.\nonumber \\ \end{aligned}$$

(57c)

The above developments are not analytically investigated in this study: They have been reported here for a sake of completeness and to precisely demonstrate the results of Sect. 2.3.

Appendix C: On the plate (w, F)-formulation ROM

In the literature dealing with analytical models of plates, the $(\varvec{u},w)$-formulation of the previous section is never used since it would lead to tedious—maybe impossible—computations in an analytical context (see Eq. (51)) and also because there are three unknown displacement fields (w and the two components of $\varvec{u}$). In most of the cases, the in-plane inertia is neglected and Eq. (11b) reduces to ${\mathbf {div}}\,\varvec{N}=\varvec{0}$, which enables the introduction of an Airy stress function $F(\varvec{r},t)$ defined by:

$$\begin{aligned} \Delta F\varvec{1} + \varvec{\nabla }\varvec{\nabla }F = \varvec{N}. \end{aligned}$$

(58)

Then, by adding a compatibility condition, one obtains the following (w, F)-formulation (all details can be found in [14]):

$$\begin{aligned} \ddot{w} + \Delta \Delta w&= \varepsilon \phi (w,F) + p(\varvec{r},t) \end{aligned}$$

(59a)

$$\begin{aligned} \Delta \Delta F&= -\frac{1}{2} \phi (w,w) \end{aligned}$$

(59b)

where the overbars have been dropped and where $\phi (\cdot ,\cdot )$ is a bilinear operator [14]. Similarly to the beam case, the transverse displacements and the force function are expanded on a linear basis of vibration modes $\varPhi _k$ and $\varUpsilon _j$:

$$\begin{aligned}&w(\varvec{r},t) = \sum _{k=1}^{N_w} \varPhi _k(\varvec{r}) q_k(t) \quad \text {and} \nonumber \\&\qquad F(\varvec{r},t) = \sum _{j=1}^{N_F} \varUpsilon _j(\varvec{r}) \eta _j(t) \end{aligned}$$

(60)

where the $q_k$ and $\eta _j$ are time-dependent modal coordinates, respectively, associated with bending and in-plane eigenmodes, which verify:

$$\begin{aligned} \Delta \Delta \varPhi _{k} - \omega ^2_k \varPhi _k&= 0, \end{aligned}$$

(61a)

$$\begin{aligned} \Delta \Delta \varUpsilon _{j} + \zeta _j^4 \varUpsilon _j&= 0. \end{aligned}$$

(61b)

After multiplying equation (59a) by a mode $\varPhi _l$, equation (59b) by a mode $\varUpsilon _m$ and integrating on the surface of the plate, the orthogonality property of the eigenmodes yields:

$$\begin{aligned}&\ddot{q}_k + \omega _k^2 q_k - \varepsilon \sum _{p=1}^{N_w} \sum _{j=1}^{N_F} E_{rj}^k q_r \eta _j = Q_k(t) \end{aligned}$$

(62a)

$$\begin{aligned}&\zeta _j^4 \eta _j = - \frac{1}{2}\sum _{p=1}^{N_w} \sum _{q=1}^{N_w} H_{pq}^j q_p q_q, \end{aligned}$$

(62b)

where nonlinear quadratic coefficients $(E_{rj}^k, H_{pq}^j)$ and modal load $Q_k$ are defined in “Appendix C”. Finally, eliminating $\eta _j(t)$ between Eqs (62a, b) leads to the same set of $N_w$ coupled transverse oscillators with cubic nonlinearities than in the case of beams, Eq. (9), with the following values of the condensed cubic coefficients:

$$\begin{aligned} \varGamma _{pqr}^k = \sum _{j=1}^{N_F} \frac{E_{rj}^kH_{pq}^j}{2\zeta _j^4}. \end{aligned}$$

(63)

Again, the above-defined nonlinear coefficients depend on the mode normalization, defined by Eq. (65).

The analytical expressions of the coefficients of nonlinear terms in Eq. (63) are:

$$\begin{aligned} E_{rj}^k= & {} \frac{\displaystyle {\int _{\mathcal {S}} \varPhi _k L (\varPhi _r, \varUpsilon _j) \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}, \nonumber \\ H_{pq}^j= & {} \frac{\displaystyle {\int _{\mathcal {S}} \varUpsilon _j L(\varPhi _p, \varPhi _q) \,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varUpsilon _j^2 \,\text {d}S}}, \nonumber \\ Q_k (t)= & {} \frac{\displaystyle {\int _{\mathcal {S}} \varPhi _{k} p(\varvec{r},t)\,\text {d}S}}{\displaystyle {\int _{\mathcal {S}} \varPhi _k^2 \,\text {d}S}}. \end{aligned}$$

(64)

The modes are here normalized as:

$$\begin{aligned} \int _{\mathcal {S}} \varPhi _k^2\,\text {d}S=\int _{\mathcal {S}} \varUpsilon _p^2\,\text {d}S=1. \end{aligned}$$

(65)

Appendix D: Numerical values of beam and plate cubic ROM coefficients

The numerical values of the $\varGamma _{ijl}^k$ coefficients of Eq. (9), in the case of the clamped–clamped beam and the circular plate, are gathered in Table 10. They have been computed by the analytical models (Eq. (10) and (63)) and are identical to those computed by the STEP (Sect. 3.2).

Appendix E: Details of STEP

We develop here the details to compute only the nonzero coefficients of (23) with the method of [26]. We refer to the notations $C_{pi}^k$, $D_{ijl}^k$ and $G_{ij}^p$ of Eq. (7). Four distinct steps are necessary, by separating bending modes (BM) and in-plane modes (MM). We also consider unitary modal masses ($m_r=1\;\forall r$).

• Step 1 Imposing a displacement on a single BM, $\varvec{x}_1=\lambda \varvec{\varPhi }_\alpha$, and expanding the result on either a BM $\varvec{\varPhi }_k$ or a MM $\varvec{\varPsi }_p$ leads to:

  $$\begin{aligned} \lambda ^3 D_{\alpha \alpha \alpha }^k&= \varvec{\varPhi }_k^{{\text {T}}} \varvec{f}_\text {nl}(\lambda \varvec{\varPhi }_\alpha ), \end{aligned}$$

  (66)
  $$\begin{aligned} \lambda ^2 G_{\alpha \alpha }^p&= \varvec{\varPsi }_p^{{\text {T}}} \varvec{f}_\text {nl}(\lambda \varvec{\varPhi }_\alpha ). \end{aligned}$$

  (67)

  Consequently, only $N_w$ static computations are necessary to obtain coefficients $D_{\alpha \alpha \alpha }^k$ and $G_{\alpha \alpha }^p$.

• Step 2 Imposing displacements on two BM, $\varvec{x}_2=\lambda _\alpha \varvec{\varPhi }_\alpha \pm \lambda _\beta \varvec{\varPhi }_\beta$, with $\beta >\alpha$, and expanding the result on either a BM $\varvec{\varPhi }_k$ or a MM $\varvec{\varPsi }_p$ leads to:

  $$\begin{aligned} \lambda _\alpha ^2\lambda _\beta D^k_{\alpha \alpha \beta } + \lambda _\alpha \lambda _\beta ^2 D^k_{\alpha \beta \beta } =&\varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta ) \nonumber \\&- \lambda _\alpha ^3 D_{\alpha \alpha \alpha }^k - \lambda _\beta ^3 D_{\beta \beta \beta }^k, \end{aligned}$$

  (68)
  $$\begin{aligned} -\lambda _\alpha ^2\lambda _\beta D^k_{\alpha \alpha \beta } + \lambda _\alpha \lambda _\beta ^2 D^k_{\alpha \beta \beta } =&\varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha - \lambda _\beta \varvec{\varPhi }_\beta )\nonumber \\&- \lambda _\alpha ^3 D_{\alpha \alpha \alpha }^k + \lambda _\beta ^3 D_{\beta \beta \beta }^k \end{aligned}$$

  (69)
  $$\begin{aligned} \lambda _\alpha \lambda _\beta G_{\alpha \beta }^p =&\varvec{\varPsi }_p^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta ) \nonumber \\&- \lambda _\alpha ^2 G_{\alpha \alpha }^p + \lambda _\beta ^2 G_{\beta \beta }^p \end{aligned}$$

  (70)

  where the last part of the second members is known from the first step. At this step, since $\beta >\alpha$, $N_w(N_w-1)$ static computations are required.

• Step 3 Imposing displacements on one BM and one MM, $\varvec{x}_3=\lambda _\alpha \varvec{\varPhi }_\alpha +\lambda _\beta \varvec{\varPsi }_\beta$, and expanding the result on a BM $\varvec{\varPhi }_k$ leads to:

  $$\begin{aligned} \lambda _\alpha \lambda _\beta C_{\alpha \beta }^k = \varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta ) - \lambda _\alpha ^3 D_{\alpha \alpha \alpha }^k \end{aligned}$$

  (71)

  Since $\alpha =1,\ldots N_w$ and $\beta =1,\ldots N_u$, the computation of the coefficients $C_{\alpha \beta }^k$ thus requires $N_wN_u$ static computations.

• Step 4 Imposing a displacement on a three BM, $\varvec{x}_4=\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta + \lambda _\gamma \varvec{\varPhi }_\gamma$, and expanding the result on a BM $\varvec{\varPhi }_k$ leads to:

  $$\begin{aligned} \lambda _\alpha \lambda _\beta \lambda _\gamma D_{\alpha \beta \gamma }^k&= \varvec{\varPhi }_k^{{\text {T}}}\varvec{f}_\text {nl}(\lambda _\alpha \varvec{\varPhi }_\alpha + \lambda _\beta \varvec{\varPhi }_\beta + \lambda _\gamma \varvec{\varPhi }_\gamma ) \nonumber \\&- \sum _{\begin{array}{c} i,j,l\in \{\alpha ,\beta ,\gamma \}\\ l\ge j\ge i\\ ijl\ne \alpha \beta \gamma \end{array}}\lambda _i\lambda _j\lambda _l D_{ijl}^k. \end{aligned}$$

  (72)

  This computation of the $D_{\alpha \beta \gamma }^k$ coefficients thus requires $N_w^3/6-N_w^2/2+N_w/3$ static computations.

Appendix F: Computation of the energy for the FEPs

The nonlinear part of the potential energy in Eq. (41) writes:

$$\begin{aligned} {\mathcal {V}}_{nl}&= \sum _{i=1}^{N _w}\varGamma _{iii}^i \frac{q_i^4}{4} + \sum _{i=1}^{N_w} \sum _{j>i}^{N_w} \bigg (\varGamma _{iij}^i \frac{q_i^3 q_j}{3}+\varGamma _{iij}^{j}q_{i}^2q_{j}^{2} \nonumber \\&\quad + \varGamma _{ijj}^j \frac{q_j^3 q_i}{3} \bigg ) \nonumber \\&\quad + \sum _{i=1}^{N_w} \sum _{j>i}^N \sum _{k>j}^{N_w} \bigg ( \frac{\varGamma _{ijk}^i}{2} q_i^2 q_j q_k + \frac{\varGamma _{ijk}^j}{2} q_i q_j^2 q_k \nonumber \\&\quad + \frac{\varGamma _{ijk}^k}{2} q_i q_j q_k^2 \bigg )\nonumber \\&\quad + \sum _{i=1}^{N_w} \sum _{j>i}^{N_w} \sum _{k>j}^{N_w} \sum _{l=1}^{N_w} \varGamma _{ijk}^l q_i q_j q_k q_l . \end{aligned}$$

(73)

To obtain this equation, the starting point is the general expression of a dynamical system with cubic nonlinearities:

$$\begin{aligned} \ddot{q}_k + \omega _k^2 q_k + \sum _{i=1}^{N_w} \sum _{j=i}^{N_w} \sum _{l=j}^{N_w} \varGamma _{ijl}^{k} q_i q_j q_l = Q_k, \end{aligned}$$

(74)

which can also be written $\ddot{\varvec{q}} + \varvec{f}(\varvec{q}) = 0$, where $\varvec{f}$ denotes the internal forces vector. It derives from a potential and can be integrated over time if and only if the following condition on the crossed derivatives is verified:

$$\begin{aligned} \frac{\partial f_i}{\partial q_j} = \frac{\partial f_j}{\partial q_i} \quad \forall i \ne j. \end{aligned}$$

(75)

According to the developments of [14], it is established for some classical boundary conditions of plates—including the clamped one—that the symmetry properties of the bilinear operator L lead to the following equality between the nonlinear coefficients of the (w, F)-formulation ROM presented in “Appendix B”:

$$\begin{aligned} H_{pq}^j = E_{pj}^q, \qquad H_{pq}^j = H_{qp}^j. \end{aligned}$$

(76)

It results after some developments to some equalities between the non-upper triangular form coefficients ${\bar{\varGamma }}_{ijl}^k, {i,j,l,k} \in [1,N_w]$, which are written:

$$\begin{aligned} {\bar{\varGamma }}_{ijl}^k {=}{} \mathbf {\bar{\varGamma }}_{jil}^k = {\bar{\varGamma }}_{kjl}^i = {\bar{\varGamma }}_{klj}^i = {\bar{\varGamma }}_{lki}^j {=} {\bar{\varGamma }}_{kli}^j = {\bar{\varGamma }}_{jki}^l = {\bar{\varGamma }}_{kji}^l, \end{aligned}$$

(77)

thus, the upper triangular form yields

$$\begin{aligned}&\varGamma _{iij}^i = 3 \varGamma _{iii}^j, \quad \varGamma _{ijj}^i = \varGamma _{iij}^j,\quad \varGamma _{ijj}^j = 3\varGamma _{jjj}^i \quad \forall j>i \nonumber \\&\varGamma _{ijl}^j = 2 \varGamma _{jjl}^i = 2\varGamma _{ijj}^l, \quad \varGamma _{ijl}^i = 2 \varGamma _{iij}^l = 2\varGamma _{iil}^j, \nonumber \\&\varGamma _{ijl}^l = 2 \varGamma _{ill}^j =2 \varGamma _{jll}^i \quad \forall l>j>i\nonumber \\&\varGamma _{ijl}^k = \varGamma _{ijk}^l = \varGamma _{ilk}^j = \varGamma _{jlk}^i \quad \forall k>l>j>i, \end{aligned}$$

(78)

which allows to verify the condition of Eq. (75). The general expression of the energy in Eq. (73) is then obtained by multiplying the equation of the kth oscillator of Eq. (74) by the modal velocity ${\dot{q}}_k$ and integrating over time.