Hardening/softening behavior and reduced order modeling of nonlinear vibrations of rotating cantilever beams

Abstract

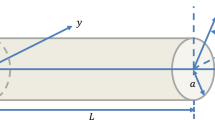
This work addresses the large amplitude nonlinear vibratory behavior of a rotating cantilever beam, with applications to turbomachinery and turbopropeller blades. The aim of this work is twofold. Firstly, we investigate the effect of rotation speed on the beam nonlinear vibrations and especially on the hardening/softening behavior of its resonances and the appearance of jump phenomena at large amplitude. Secondly, we compare three models to simulate the vibrations. The first two are based on analytical models of the beam, one of them being original. Those two models are discretized on appropriate mode basis and solve by a numerical following path method. The last one is based on a finite-element discretization and integrated in time. The accuracy and the validity range of each model are exhibited and analyzed.

Appendices

Appendix 1: Nonlinear coefficients for the inextensible model

The coefficients $A_p^k$, $B_{p}^k$, $\Gamma _{pqr}^k$, $\Lambda _{pqr}^k$ et $\Pi _{pqr}^k$ and the modal forcing $p_k$ are given by

$$\begin{aligned}&A_{p}^{k}= \int _{0}^{1}{\left[ \left( \Phi '_{p}e_{s}\right) ''+\Phi '''_{p}e_{s}\right] '\Phi _{k}}\,{\text {d}}X,\end{aligned}$$

(72a)

$$\begin{aligned}&B_{p}^{k}=\int _{0}^{1}\left[ \left( \Phi '_{p}\int _{1}^{X}{\int _{0}^{X}{e_{s}}\,\text {d}X}{\text {d}}X\right) '\right. \nonumber \\&\quad \left. -\left( \Phi '_{p}\left( 1- e_{s}\right) \int _{1}^{X}{\left( R+X\right) }\,{\text {d}}X\right) '\right] \Phi _{k}\,{\text {d}}X ,\end{aligned}$$

(72b)

$$\begin{aligned}&\Gamma _{pqr}^{k}=\int _{0}^{1}{\left[ \Phi '_{p}\Phi ''_{q}\Phi ''_{r}+\Phi '''_{p}\Phi '_{q}\Phi '_{r}\right] '\Phi _{k}}\,{\text {d}}X ,\end{aligned}$$

(72c)

$$\begin{aligned}&\Lambda _{pqr}^{k}=\int _{0}^{1}\left[ \Phi '_{p}\Phi '_{q}\Phi '_{r}\int _{1}^{X}{\left( R+X\right) }\,{\text {d}}X\right. \nonumber \\&\left. -\Phi '_{p}\int _{1}^{X}\int _{0}^{X}{\Phi '_{q}\Phi '_{r}}\,{\text {d}}X{\text {d}}X \right] '\Phi _{k}\,{\text {d}}X, \end{aligned}$$

(72d)

$$\begin{aligned}&\Pi _{pqr}^{k}=\int _{0}^{1}{\left[ \Phi '_{p}\int _{1}^{X}{\int _{0}^{X}{\Phi '_{q}\Phi '_{r}}}\,{\text {d}}X{\text {d}}X\right] '\Phi _{k}}\,{\text {d}}X, \end{aligned}$$

(72e)

$$\begin{aligned}&p_k=\int _0^1 p\,\Phi _k {\text {d}}X. \end{aligned}$$

(72f)

Appendix 2: Finite-element details

Details of the beam finite-element discretization of Sect. 4 are specified here, by starting from the variational formulation of Eq. (22). In the following, a superscript or a subscript e refers to elementary quantities. The generalized displacements are discretized using linear shape functions. Thus, axial displacement, transverse displacements and fiber rotations on one finite element of length $L_e$ are gathered into $\mathbf {u}^e=[u\;w\;\theta ]^{{\text {T}}}$ and related to the elementary dofs vector $\mathbf {q}^e$ by, for all $X\in [0 \;L_e]$:

$$\begin{aligned} \mathbf {u}^e(X) = \mathbf {N}(X)\,\mathbf {q}^e \end{aligned}$$

(73)

where $\mathbf {q}^e=[u_1\;w_1\;\theta _1\;u_2\;w_2\;\theta _2]^{{\text {T}}}$,

$$\begin{aligned} \mathbf {N}(X)=\left[ \begin{array}{cccccc} N_{1} &{} 0 &{} 0 &{} N_{2} &{} 0 &{} 0 \\ 0 &{} N_{1} &{} 0 &{} 0 &{} N_{2} &{} 0 \\ 0 &{} 0 &{} N_{1} &{} 0 &{} 0 &{} N_{2} \end{array} \right] , \end{aligned}$$

(74)

and $u_1$, $w_1$ and $\theta _1$ (respectively, $u_2$, $w_2$ and $\theta _2$) correspond to the first (respectively, second) node of the beam element. The two shape functions are:

$$\begin{aligned} N_1(X)=1-\frac{X}{L_e},\quad N_2(X)=\frac{X}{L_e}. \end{aligned}$$

(75)

Therefore, the discretized expressions of strains e, $\gamma$ and $\kappa$ (Eqs. (15a–c)) are found to be:

$$\begin{aligned} e^e&=\left( 1+\frac{u_2-u_1}{L}\right) \cos \theta + \left( \frac{w_2-w_1}{L}\right) \sin \theta -1, \end{aligned}$$

(76a)

$$\begin{aligned} \gamma ^e&= \left( \frac{w_2-w_1}{L}\right) \cos \theta - \left( 1+\frac{u_2-u_1}{L}\right) \sin \theta ,\end{aligned}$$

(76b)

$$\begin{aligned} \kappa ^e&= \frac{\theta _2-\theta _1}{L}. \end{aligned}$$

(76c)

They are gathered into the elementary strain vector $\mathbf {e}=[e^e\;\gamma ^e\;\kappa ^e]^{{\text {T}}}$ which can be written as $\mathbf {e}(X)=\mathbf {B}(X,\mathbf {q}^e)\mathbf {q}^e$, with $\mathbf {B}$ the elementary discretized gradient matrix.

The works of the internal forces, the external forces and the acceleration forces [Eqs. (23a–c)] are discretized as follows:

$$\begin{aligned} \delta \mathcal {W}_a&= \int _0^{L_e} \delta \mathbf {u}^{e{\text {T}}}\,\mathbf {J}\,\ddot{\mathbf {u}}^e = \delta \mathbf {q}^{e{\text {T}}} \underbrace{\left( \int _0^{L_e}\mathbf {N}^{{\text {T}}}\mathbf {J}\mathbf {N}\,\text {d}X\right) }_{\mathbf {M}^e}\mathbf {q}^e, \\ \delta \mathcal {W}_i&= - \int _0^{L_e} \left( EAe\delta e + kG\gamma \delta \gamma + EI\kappa \delta \kappa \right) \,\text {d}X \\&= - \int _0^{L_e}\delta \mathbf {e}^{{\text {T}}}\mathbf {C}\mathbf {e}\,\text {d}X \\&=- \delta \mathbf {q}^{e{\text {T}}} \underbrace{\left( \int _0^{L_e}\mathbf {B}^{{\text {T}}}\mathbf {C}\mathbf {B}\mathbf {q}^e\,\text {d}X\right) }_{\mathbf {f}_\text {int}^e(\mathbf {q}^e)},\\ \delta \mathcal {W}_e&=\underbrace{\rho \Omega ^2 \int _0^{L_e}\left[ A\left( R+X+u\right) \;0 \; -\frac{1}{2}I\sin \left( 2\theta \right) \right] \mathbf {N}\,\text {d}X}_{\mathbf {f}_\Omega ^{e{\text {T}}}}\,\delta \mathbf {q}^e \\&+ \underbrace{\int _0^{L_e} \left[ n \;\; p \;\; q\right] \mathbf {N}\,\text {d}X}_{\mathbf {f}_\text {ext}^{{\text {T}}}}\,\delta \mathbf {q}^e. \end{aligned}$$

where

$$\begin{aligned} \mathbf {J}=\left[ \begin{array}{ccc} A &{} 0 &{} 0 \\ 0 &{} A &{} 0 \\ 0 &{} 0 &{} I \\ \end{array} \right] \quad \text {and}\quad \mathbf {C}=\left[ \begin{array}{ccc} EA &{} 0 &{} 0 \\ 0 &{} kGA &{} 0 \\ 0 &{} 0 &{} EI \\ \end{array} \right] . \end{aligned}$$

The elementary mass matrix is obtained by directly evaluating the above integral, to obtain:

$$\begin{aligned} \mathbf {M}^e=\frac{\rho L_e}{6} \left[ \begin{array}{cccccc} 2A &{} 0 &{} 0 &{} A &{} 0 &{} 0 \\ 0 &{} 2A &{} 0 &{} 0 &{} A &{} 0 \\ 0 &{} 0 &{} 2I &{} 0 &{} 0 &{} I \\ A &{} 0 &{} 0 &{} 2A &{} 0 &{} 0 \\ 0 &{} A &{} 0 &{} 0 &{} 2A &{} 0 \\ 0 &{} 0 &{} I &{} 0 &{} 0 &{} 2I \end{array} \right] . \end{aligned}$$

(77)

The integral for the internal force vector is evaluated by thanks to a reduced integration with the one-point Gauss rule at $X = L_e/2$ to avoid shear locking [6, Sect. 5.4.1]. We denote by $\bar{\theta }=(\theta _2+\theta _1)/2$, $\bar{c}=\cos \bar{\theta }$ and $\bar{s}=\sin \bar{\theta }$ the values of $\cos \theta$ and $\sin \theta$ at $X = L_e/2$. One thus obtains:

$$\begin{aligned} \mathbf {f}_\text {int}^e= & {} EA\bar{e} \left[ \begin{array}{c} -\bar{c} \\ -\bar{s} \\ \bar{\gamma }L_e/2\\ \bar{c}\\ \bar{s}\\ \bar{\gamma }L_e/2 \end{array} \right] +kGA\bar{\gamma } \left[ \begin{array}{c} \bar{s} \\ -\bar{c} \\ -\left( 1+\bar{e}\right) L_e/2\\ -\bar{s}\\ \bar{c}\\ -\left( 1+\bar{e}\right) L_e/2 \end{array} \right] \nonumber \\&+EI\bar{\kappa } \left[ \begin{array}{c} 0\\ 0 \\ -1\\ 0\\ 0\\ 1 \end{array} \right] , \end{aligned}$$

(78)

where $\bar{e}=e^e(\bar{\theta })$, $\bar{\gamma }=\gamma ^e(\bar{\theta })$ and $\bar{\kappa }=\kappa ^e(\bar{\theta })$. Then, the integral in the centrifugal force vector $\mathbf {f}_\Omega$ is evaluated with the average angle $\bar{\theta }$. The reason is that $\theta = N_{1}\theta _{1} + N_{2}\theta _{2}$, which is the exact expression of $\theta$ coming from the finite-element discretization, gives efforts as a fraction whose denominator is $\left( \theta _{1} - \theta _{2} \right) ^2$. Therefore, it may lead to tremendous efforts when the beam passes through its initial position $\left( \theta _{1} \approx \theta _{2}\right)$, whereas it is not the case since the initial position is the one where the only effort involved is those due to rotation. Using this reduced integration only for $\theta$ leads to obtain:

$$\begin{aligned} \mathbf {f}_\Omega ^e= & {} \underbrace{ \frac{1}{4}\rho I\Omega ^{2}L_e \left[ \begin{array}{c} 0 \\ 0 \\ \sin \left( 2\bar{\theta }\right) \\ 0 \\ 0 \\ \sin \left( 2\bar{\theta }\right) \end{array} \right] }_{\mathbf {f}_{\Omega }^{\text {nl}}} + \underbrace{ \frac{1}{6}\rho A\Omega ^{2}L_e \left[ \begin{array}{c} 2u_{1}+u_{2} \\ 0 \\ 0 \\ u_{1}+2u_{2} \\ 0 \\ 0 \end{array} \right] }_{\mathbf {f}_{\Omega }^{\text {lin}}}\nonumber \\&+ \underbrace{ \frac{1}{6}\rho A\Omega ^{2}L_e \left[ \begin{array}{c} L+3R \\ 0 \\ 0 \\ 2L+3R \\ 0 \\ 0 \end{array} \right] }_{\mathbf {f}_{\Omega }^{\text {cste}}} \end{aligned}$$

(79)

The elementary stiffness matrix, used for the Newton–Raphson algorithm iterations, is obtained in the following way. It is obtained by differentiating the internal force vector and the centrifugal force vector:

$$\begin{aligned} \mathbf {K}_\text {t}=\frac{\partial \mathbf {f}}{\partial \mathbf {q}}=\frac{\partial \mathbf {f}_\text {int}}{\partial \mathbf {q}}-\frac{\partial \mathbf {f}_\Omega }{\partial \mathbf {q}}=\mathbf {K}_\text {mat} + \mathbf {K}_\text {geo} - \mathbf {K}_\text {c} - \mathbf {K}_\text {gc}.\nonumber \\ \end{aligned}$$

(80)

This matrix is the sum of the material stiffness $\mathbf {K}_\text {mat}$, the geometric stiffness $\mathbf {K}_\text {geo}$, the centrifugal stiffness $\mathbf {K}_\text {c}$ and the geometric centrifugal stiffness $\mathbf {K}_\text {gc}$. Among these four contributions to the total stiffness, $\mathbf {K}_\text {geo}$ and $\mathbf {K}_\text {gc}$ are deflection dependent, whereas $\mathbf {K}_\text {mat}$ and $\mathbf {K}_\text {c}$ are linear. The material stiffness comes from the variation of the nodal displacement $\delta \mathbf {q}$ of the generalized forces while keeping the discretized gradient $\mathbf {B}$ fixed and the geometric stiffness comes from the variation of $\mathbf {B}$ while the generalized forces are kept fixed. The centrifugal stiffness stands for the constant additional stiffness due to the rotation, and the geometric centrifugal stiffness represents the deflection-dependent centrifugal effect that depends on the rotation angle $\theta$.

On then obtains, at the elementary level:

$$\begin{aligned} \frac{\partial \mathbf {f}_\text {int}^e}{\partial \mathbf {q}^e}= & {} \underbrace{\int _0^{L_e}\mathbf {B}^{{\text {T}}}\mathbf {C}\mathbf {B}\,\text {d}X}_{\mathbf {K}_{\text {mat}}} + \underbrace{\int _0^{L_e}\frac{\partial \mathbf {B}^{{\text {T}}}}{\partial \mathbf {q}^e}\mathbf {C}\mathbf {B}\mathbf {q}^e\,\text {d}X}_{\mathbf {K}_{\text {geo}}}\nonumber \\= & {} \mathbf {K}_e^e+\mathbf {K}_\gamma ^e+ \mathbf {K}_\kappa ^e \end{aligned}$$

(81)

These three contributions correspond to the tangent stiffness matrix due to the axial strain e, the shear $\gamma$ and the curvature $\kappa$, which write:

$$\begin{aligned} \mathbf {K}_e^{e}= & {} \frac{EA}{L} \left[ \begin{array}{rrrrrr} K_{1} &{} K_{3} &{} K_{4} &{} -K_{1} &{} -K_{3} &{} K_{4} \\ &{} K_{2} &{} K_{5} &{} -K_{3} &{} -K_{2} &{} K_{5} \\ &{} &{} K_{6} &{} -K_{4} &{} -K_{5} &{} K_{6} \\ &{} &{} &{} K_{1} &{} K_{3} &{} -K_{4} \\ &{} &{} &{} &{} K_{2} &{} -K_{5} \\ &{} &{} &{} &{} &{} K_{6} \end{array} \right] , \\ \mathbf {K}_\gamma ^e= & {} \frac{kGA}{L} \left[ \begin{array}{rrrrrr} K_{2} &{} -K_{3} &{} K_{7} &{} -K_{2} &{} K_{3} &{} K_{7} \\ &{} K_{1} &{} K_{8} &{} K_{3} &{} -K_{1} &{} K_{8} \\ &{} &{} K_{9} &{} -K_{7} &{} -K_{8} &{} K_{9} \\ &{} &{} &{} K_{2} &{} -K_{3} &{} -K_{7} \\ &{} &{} &{} &{} K_{1} &{} -K_{8} \\ &{} &{} &{} &{} &{} K_{9} \end{array} \right] ,\\ \quad \mathbf {K}_\kappa ^e= & {} \frac{EI}{L} \left[ \begin{array}{rrrrrr} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} 1 &{} 0 &{} 0 &{}-1 \\ &{} &{} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} 1 \end{array} \right] , \end{aligned}$$

with

$$\begin{aligned} K_{1}= & {} \bar{c}^2, \quad K_{2}=\bar{s}^2, \quad K_{3}=\bar{c}\bar{s},\\ \quad K_{4}= & {} \frac{L_e}{2}\left( \bar{e}\bar{s}-\bar{\gamma }\bar{c}\right) , \quad K_{5}=-\frac{L_e}{2}\left( \bar{e}\bar{c}+\bar{\gamma }\bar{s}\right) , \\ K_{6}= & {} \frac{L_e^{2}}{4}\left[ \bar{\gamma }^2-\bar{e}\left( \bar{e}+1\right) \right] ,\\ \quad K_{7}= & {} \frac{L_e}{2}\left[ \bar{\gamma }\bar{c}-\left( \bar{e}+1\right) \bar{s}\right] , \\ K_{8}= & {} \frac{L_e}{2}\left[ \bar{\gamma }\bar{s}+\left( \bar{e}+1\right) \bar{c}\right] , \quad \\ K_{9}= & {} \frac{L_e^{2}}{4}\left[ \left( \bar{e}+1\right) ^2-\bar{\gamma }^2\right] . \end{aligned}$$

The centrifugal stiffness $\mathbf {K}^e_\text {c}$ and the geometric centrifugal stiffness $\mathbf {K}^e_\text {gc}$ come from

$$\begin{aligned} \frac{\partial \mathbf {f}^e_\Omega }{\partial \mathbf {q}^e}=\mathbf {K}^e_\text {c}+\mathbf {K}^e_\text {gc}, \end{aligned}$$

(83)

with

$$\begin{aligned} \mathbf {K}^e_\text {c}&=\frac{1}{6}\rho AL\Omega ^2 \left[ \begin{array}{cccccc} 2 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} 2 &{} 0 &{} 0 \\ &{} &{} &{} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} 0 \end{array} \right] , \\ \quad \mathbf {K}^e_\text {gc}&=\frac{1}{4}\rho IL\Omega ^2\cos 2\bar{\theta } \left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} 1 &{} 0 &{} 0 &{} 1 \\ &{} &{} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} 1 \end{array} \right] . \end{aligned}$$

(84a)