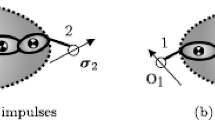1 Introduction

Efficient dynamics simulations of complex multibody systems (MBS) are of crucial importance in many areas of computer aided engineering and design. There are many examples of such systems including vehicles, biomechanical models, robots and multidisciplinary applications. Computations can be carried out by means of different types of formulations. To meet requirements for high-fidelity performance and accurate dynamics simulations of complex systems, it has become a practice to apply efficient, low order algorithms designed both for sequential and parallel computations.

The examples of efficient O(n) (n—number of bodies) recursive sequential algorithms for analysis of tree-like topology rigid body dynamics can be found in [1, 4, 5, 7, 14, 22, 36, 37, 41, 42]. Some researchers developed recursive order “O(n)” formulations dynamics simulations of multibody systems with closed loops [2, 33, 38, 39]. These algorithms gave basis for further development of efficient low order formulations.

As parallel computing resources became more available, researchers began to adapt the existing formulations or design completely new algorithms, suitable for parallel computing. The strategies enabled to decrease the turnaround time associated with computer simulations and even achieve results in real-time. The first attempts to exploit parallel strategies can be found in [6, 12, 18, 19, 25, 26].

In the literature, there are more recent ideas regarding parallel algorithms for rigid multibody dynamics simulation. Featherstone [15, 16] developed the optimal-time, logarithmic order divide and conquer algorithm (DCA) for dynamics of general multibody systems. The idea behind the formulation lies in a recursive binary assembly and disassembly of articulated bodies. The extension to closed loop systems were obtained through the application of constraint stabilization methods and proper decomposition of constraint forces. Fisette and Peterkenne [20] and independently Anderson and Duan [3] adopted the idea of a decomposition of multibody system into subchains. In [13], the authors explored the ideas of recursive coordinate reduction and presented parallel multibody algorithm with optimal logarithmic time complexity for general multibody systems applicability. The formulation, however, was not free from problems arising from the fact that some matrices lost their ranks. Yamane and Nakamura [43] developed the new assembly-disassembly algorithm, which is based on the concept of divide and conquer scheme. In work [32], Mukherjee and Anderson presented exact and non-iterative divide and conquer algorithm for forward dynamics of MBS with single and coupled loops, which incorporated neither coordinate reductions nor Lagrange multipliers. The latest comparative study on efficient sequential and parallel multibody dynamics algorithms can be found in [44] and in recent books [17, 23].

Based on the divide and conquer scheme [15], the authors presented recently parallel algorithms for general constrained MBS dynamics using augmented Lagrangian methods and mass-orthogonal projections [27–31]. The improved, extended and verified versions of the methods are proposed in this paper. The developed parallel formulations for dynamics of general multibody systems encompass efficiency, accuracy and robustness in case of analyzing systems with redundant constraints containing single or multiple kinematic loops, and which may enter singular configurations.

2 Algorithm overview

2.1 Preliminaries

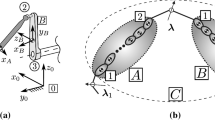
This section presents analytical derivations for the divide and conquer (DCA) algorithm based on augmented Lagrangian formulation with projections for dynamics simulation of general multibody systems (MBS). The method used here is similar to that proposed by Featherstone [15, 16], however the underlying computations are different. The parallel algorithm is composed of only two computational stages: assembly and disassembly phase. Each computational phase is connected to the binary tree associated with the topology of the mechanism. The graphical representation of the example of assembly-disassembly process for a four-link MBS is shown in Fig. 1. The first stage starts with writing of equations of motion for each body in the system and is continued until the analyzed multibody system is assembled. Subassemblies, which correspond to nodes in the graph, are constructed by traversing the binary tree from leaves to the top node. Finally, a single assembly is obtained, which is denoted as a root node of the binary tree. This node constitutes a representation of the entire multibody system modeled as a single assembly. The main pass finishes at this stage. Taking into account the boundary conditions, e.g., a connection of a chain to fixed base and free floating terminal body, the second phase is started. Traversing the binary tree from the root node to leaves, all Lagrange multipliers and bodies’ accelerations are computed in the system. This brief description of the DCA algorithm will help to understand the proposed formulations. The sequence of derivations will correspond to this short review.

Fig. 1
figure 1

Recursive binary assembly and disassembly of a four-link multibody system

Full size image

2.2 Assembly phase

2.2.1 Equations of motion for two articulated bodies

To aid in the subsequent derivations, consider a system of two rigid bodies connected by a joint, as depicted in Fig. 2. Each body in the system is characterized by a 7×1 vector of absolute coordinates \(\mathbf {q}_{i}=[\mathbf {r}_{i}^{T}\ \mathbf {p}_{i}^{T}]^{T}\), where index i=1,…,n is the number of bodies in the system. Vector r i describes a position of the origin (located in body’s mass center) of the reference frame rigidly attached to body i with respect to global reference frame and p i is a vector of Euler parameters representing orientation of the local frame. Moreover, Lagrange multipliers λ 1, λ 2, λ are associated with constraint forces in joints (Fig. 2).

Fig. 2
figure 2

Two articulated bodies

Full size image

Equations of motion for bodies A and B can be written in the form, which takes into account Euler parameter representation of rotations:

$$ \mathbf {M}^{A}\ddot{\mathbf {q}}^{A} +{\boldsymbol {\Phi}_{\mathbf {q}^{A}}^{1}}^{T} \boldsymbol {\lambda}_{1} +\boldsymbol {\Phi}_{\mathbf {q}^{A}}^{T}\boldsymbol {\lambda} +{\boldsymbol {\Phi}_{\mathbf {q}^{A}}^{N}}^{T}{\lambda}_{A}^{N} =\mathbf {Q}^{A}, $$
(1)
$$ \mathbf {M}^{B}\ddot{\mathbf {q}}^{B} +\boldsymbol {\Phi}_{\mathbf {q}^{B}}^{T} \boldsymbol {\lambda} +{\boldsymbol {\Phi}_{\mathbf {q}^{B}}^{2}}^{T}\boldsymbol { \lambda}_{2} +{\boldsymbol {\Phi}_{\mathbf {q}^{B}}^{N}}^{T}{ \lambda}_{B}^{N} =\mathbf {Q}^{B}. $$
(2)

where the inertia matrices M A and M B are 7×7 quantities, which are known to be singular [21, 34], vectors Q A, Q B are applied, position and velocity dependent forces, Lagrange multipliers λ 1, λ 2, λ are associated with joint constraint equations Φ 1, Φ 2, Φ, and \({\lambda}_{A}^{N}\), \({\lambda}_{B}^{N}\) are Lagrange multipliers related to Euler parameters normalization constraints Φ N for body A and B. The joint between the bodies imposes the constraint equations that could be expressed at the acceleration level as follows:

$$ \ddot{\boldsymbol {\varPhi}}= \boldsymbol {\Phi}_{\mathbf {q}^{A}}\ddot{\mathbf {q}}^{A}+ \boldsymbol {\Phi}_{\mathbf {q}^{B}}\ddot{\mathbf {q}}^{B}+ \boldsymbol { \upgamma}^{AB}=\boldsymbol {0}, $$
(3)

where vector γAB is that part of acceleration constraint equations which are dependent on positions and velocities. The Euler parameters normalization constraints can be also written as a second derivatives with respect to time:

$$ \ddot{{\varPhi}}_{A}^{N}= \boldsymbol {\Phi}_{\mathbf {q}^{A}}^{N} \ddot{\mathbf {q}}^{A}+{\gamma}^{N}_{A}={0}, $$
(4)
$$ \ddot{{\varPhi}}^{N}_{B}= \boldsymbol {\Phi}_{\mathbf {q}^{B}}^{N} \ddot{\mathbf {q}}^{B}+{\gamma}^{N}_{B}={0}. $$
(5)

To apply the divide and conquer scheme, it is required to evaluate the accelerations of bodies A and B (see [15, 29]). The matrices M A and M B are not invertible in Eqs. (1) and (2). To overcome this difficulty, augmented Lagrangian formulation is employed [10, 11, 24, 35], which leads to the following Lagrange multipliers iterative approximation:

(6)
(7)
(8)

where λ ∗, \({\lambda}^{N*}_{A}\) and \({\lambda}^{N*}_{B}\) are Lagrange multipliers obtained from the previous iteration and multipliers without star sign are related to the current iteration. We assume that λ ∗=0, \({\lambda}^{N*}_{A}=0\), \({\lambda}^{N*}_{B}=0\) for the initial iteration. The matrices \(\boldsymbol {\upalpha}=\alpha \mathbf {I}=\operatorname{diag}(\alpha)\), μ and Ω are diagonal matrices that contain values of the large penalty numbers, natural frequencies and damping ratios of the system added to each constraint to fulfill constraint equations [9–11]. Let us substitute Eqs. (6), (7), and (8) to Eqs. (1) and (2) to obtain the following result:

(9)
(10)

Equations (9) and (10) form a basis for further derivations. They are starting point for the main pass phase. In contrast to Eqs. (1) and (2), relations (9) and (10) can be solved for \(\ddot{\mathbf {q}}^{A}\) and \(\ddot{\mathbf {q}}^{B}\), respectively. The encountered leading matrices are symmetric and positive definite, therefore, they are invertible, even in situations when constraint Jacobian matrices lose their rank.

2.2.2 Equations of motion for the system of articulated bodies

The procedure of elimination of Lagrange multipliers between two bodies presented in the preceding subsection can be generalized and repeated for the larger set of articulated bodies. Consider a system of rigid bodies A and B interconnected by joints, as shown in Fig. 3.

Fig. 3
figure 3

System of articulated rigid bodies

Full size image

The system is under influence of various acceleration-independent forces and its state is known. Three Lagrange multipliers associated with joints are specified. Those with subscript 1 and 2 are used to interact with other subsystems in the multibody system (MBS) and the multipliers between the articulated bodies A and B serve as those, which are eliminated during the computations. The generalization of Eqs. (9) and (10) may be written as follows:

(11)
(12)

and

(13)
(14)

The objective of the following algebraic manipulations is to obtain equations of motion for the set C, in the form:

(15)
(16)

Again, unknown Lagrange multipliers between the sets of bodies A and B can be found from the iterative process:

$$ \boldsymbol {\lambda}=\boldsymbol {\lambda}^{*}+ \boldsymbol {\upalpha}\bigl(\boldsymbol { \Phi}_{\mathbf {q}_{2}^{A}}\ddot{\mathbf {q}}_{2}^{A}+ \boldsymbol {\Phi}_{\mathbf {q}_{1}^{B}} \ddot{\mathbf {q}}_{1}^{B}+\overline{\boldsymbol {\upgamma}}^{AB}\bigr). $$
(17)

Multiplying Eq. (17) by \(\boldsymbol {\upalpha}^{-1}=\frac{1}{\alpha} \mathbf {I}\) and inserting accelerations from Eqs. (12), (13) to Eq. (17) yields:

(18)

where I is the identity matrix of the proper dimension. The relations (18) can be solved in terms of Lagrange multipliers between the sets of bodies A and B:

(19)

Let us define a matrix C as follows:

(20)

Closer look at matrix in Eq. (20) reveals that the inversion always exists, even when constraint Jacobian matrices become rank deficient. Substituting Eq. (19) into Eq. (12) and taking into account Eq. (20), we obtain:

(21)

where

(22)

Similarly, we can insert Eq. (19) into Eq. (13) taking into account Eq. (20):

(23)

where

(24)

The final step is to substitute accelerations from Eqs. (21) and (23) into Eqs. (11) and (14), respectively:

(25)
(26)

By gathering appropriate matrix coefficients and comparing Eq. (15) and (16) together with Eqs. (25) and (26), the following relations are obtained:

(27)
$$ \mathbf {M}_{12}^{C}=\mathbf {M}_{12}^{A} \bigl(\mathbf {M}_{22}^{A}\bigr)^{-1} \boldsymbol { \Phi}_{\mathbf {q}_{2}^{A}}^{T}\mathbf {C}\boldsymbol {\Phi}_{\mathbf {q}_{1}^{B}} \bigl( \mathbf {M}_{11}^{B}\bigr)^{-1}\mathbf {M}_{12}^{B}, $$
(28)
(29)
(30)

and

(31)
(32)

Relations (27) to (32) are used for the first computational stage called assembly phase. The recursive formulas are exploited until the whole MBS is constructed according to the binary tree associated with mechanism decomposition.

2.3 Disassembly phase

The assembly phase finishes when the root node of the binary tree is achieved. At this computational stage, the equations of motion for the whole multibody system can be expressed in the general form, which is similar to Eq. (15) and Eq. (16):

(33)
(34)

The quantity \(\ddot{\mathbf {q}}_{1}^{C}\) is the acceleration of the first body in the system (body 1 from the set A in Fig. 3) and \(\ddot{\mathbf {q}}_{2}^{C}\) is the acceleration of the last body (body 2 from the set B in Fig. 3). Lagrange multipliers λ 1 and λ 2 correspond to constraints connecting first and last body with topological parent and child bodies, respectively, provided they exist. There are three different boundary cases associated with the root node of the binary tree:

  1. 1.

    λ 1=0, λ 2=0.

    Taking into account Eqs. (33) and (34), the accelerations can be evaluated from the following system of linear equations:

    $$ \left [\begin{array}{c@{\quad }c} \mathbf {M}_{11}^{C} & \mathbf {M}_{12}^{C} \\[3pt] \mathbf {M}_{21}^{C} & \mathbf {M}_{22}^{C} \end{array} \right ] \left [\begin{array}{c} \ddot{\mathbf {q}}_{1}^{C} \\[3pt] \ddot{\mathbf {q}}_{2}^{C}\end{array} \right ] = \left [\begin{array}{c} \mathbf {Q}_{1}^{C} \\[3pt] \mathbf {Q}_{2}^{C} \end{array} \right ]. $$
    (35)

    The matrix coefficients \(\mathbf {M}_{11}^{C}\) and \(\mathbf {M}_{22}^{C}\) are symmetric and positive definite, moreover \(\mathbf {M}_{12}^{C}=(\mathbf {M}_{12}^{C})^{T}\). The accelerations \(\ddot{\mathbf {q}}_{1}^{C}\) and \(\ddot{\mathbf {q}}_{2}^{C}\) can be easily evaluated from Eq. (35) to begin disassembly phase. The case can be used for the simulation of free-floating systems.

  2. 2.

    λ 1≠0 i λ 2=0 or inversely.

    The Lagrange multipliers λ 1 can be approximated from the process (6) or (17) as follows:

    $$ \boldsymbol {\lambda}_{1}=\boldsymbol {\lambda}_{1}^{*}+\boldsymbol {\upalpha}\bigl(\boldsymbol {\Phi}_{\mathbf {q}_{1}^{C}}^{1}\ddot{\mathbf {q}}_{1}^{C}+ \overline{\boldsymbol {\gamma}}^{AB}_{1}\bigr). $$
    (36)

    Inserting Eq. (36) to (33) and taking into account λ 2=0 yields:

    (37)

    Again the leading matrix of coefficients from the linear system of Eqs. (37) is invertible. The case can be applied to the simulation of various tree-like multibody systems.

  3. 3.

    λ 1≠0 and λ 2≠0.

    The Lagrange multipliers λ 1 and λ 2 can be obtained from the approximation similar to that in Eq. (36):

    (38)
    (39)

    Inserting Eq. (38) into (33) and Eq. (39) into (34) yields:

    (40)

    Again the matrix coefficients in linear system of Eqs. (40) are symmetric and positive definite, thus they are invertible. This case can be applied for analysis of general closed loop multibody systems.

The process of assembly starts with equations of motion for individual bodies in the system and is continued until the whole mechanism is composed. Subassemblies, which correspond to nodes in the graph, are constructed by traversing the binary tree, according to Eqs. (27)–(32). Finally, the procedure for solving the equations of motion of the root node using the boundary conditions described in this subsection is employed. Traversing the tree from root node to leaves, all accelerations are computed according to Eq. (21) and Eq. (23). Moreover, if it is needed, Lagrange multipliers can be evaluated using Eq. (17) or Eq. (19).

3 Mass-orthogonal projections

3.1 Introduction

Derived parallel divide and conquer scheme possesses good overall characteristics and robustness in case of general multibody dynamics simulations. However, the formulation does not enforce simultaneously the error control on position and velocity constraints. In order to overcome these drawbacks, mass-orthogonal projections in positions and velocities are employed for further improvements [10, 11]. The process of correction of the state variables is numerically expensive. The projections in positions and velocities are expressed in a form of separate algorithms, which maintain the divide and conquer structure [27]. The Appendix accompanying the paper may be helpful in understanding some of the following relations.

3.2 Projections in positions

During the integration process, vector of position coordinates q ∗ may not satisfy position constraint equations. In order to correct bodies’ positions, mass-orthogonal projections of the solution to the constraint manifold are performed [10]. Consider again the system of two rigid bodies connected by a joint, as depicted in Fig. 2. The projections in positions [10, 27] can be written in a form, which is similar to that expressed in Eqs. (1) and (2) (see Eq. (93) in the Appendix):

(41)
(42)

where vectors λ (with and without subscripts or superscripts) are associated with the problem of constrained minimization of the functional

$$V=\frac{1}{2}(\mathbf {q}-\mathbf {q}_*)^T\mathbf {M}(\mathbf {q}-\mathbf {q}_*) $$

subjected to position constraint equations Φ(q,t)=0 [10, 27], whereas Δq A and Δq B are unknown position corrections. Constraint equations between body A and B can be written as

$$ \boldsymbol {\Phi}\bigl(\mathbf {q}^{A},\mathbf {q}^{B},t\bigr)=\boldsymbol {0}. $$
(43)

Euler parameters normalization constraint equations for body A and B can be expressed as

$$ {\varPhi}_{A}^{N}\bigl(\mathbf {q}^{A} \bigr)={0}, \qquad {\varPhi}_{B}^{N}\bigl( \mathbf {q}^{B}\bigr)={0}. $$
(44)

Lagrange multipliers in Eqs. (41) and (42) can be evaluated by using the following iterative approximation (see Eq. (100) in the Appendix):

(45)
(46)
(47)

where vectors λ with the asterisk sign are quantities evaluated in previous iteration. We assume λ ∗=0, \({\lambda}^{N*}_{A}=0\), \({\lambda}^{N*}_{B}=0\) for initial iteration. Inserting Eqs. (45), (46), and (47) into Eqs. (41) and (42) yields:

(48)
(49)

It should be emphasized that matrix coefficients at position increments are similar to that expressed in Eqs. (9), (10) and possess the same features. During the projections in positions, these values have to be evaluated only once per integration step. Equations (48) and (49) can be generalized for the system of articulated bodies from Fig. 3 as follows:

$$ \mathbf {M}_{11}^{A}\Delta{ \mathbf {q}}_{1}^{A}+ \mathbf {M}_{12}^{A}\Delta{ \mathbf {q}}_{2}^{A}+ {\boldsymbol {\Phi}_{\mathbf {q}_{1}^{A}}^{1}}^{T}\boldsymbol { \lambda}_{1}=\mathbf {Q}_{1}^{A}, $$
(50)
$$ \mathbf {M}_{21}^{A}\Delta{ \mathbf {q}}_{1}^{A}+ \mathbf {M}_{22}^{A}\Delta{ \mathbf {q}}_{2}^{A}+ \boldsymbol {\Phi}_{\mathbf {q}_{2}^{A}}^{T}\boldsymbol {\lambda}=\mathbf {Q}_{2}^{A}, $$
(51)

and

$$ \mathbf {M}_{11}^{B}\Delta{ \mathbf {q}}_{1}^{B}+ \mathbf {M}_{12}^{B}\Delta{ \mathbf {q}}_{2}^{B}+ \boldsymbol {\Phi}_{\mathbf {q}_{1}^{B}}^{T}\boldsymbol {\lambda}=\mathbf {Q}_{1}^{B} , $$
(52)
$$ \mathbf {M}_{21}^{B}\Delta{ \mathbf {q}}_{1}^{B}+ \mathbf {M}_{22}^{B}\Delta{ \mathbf {q}}_{2}^{B}+ {\boldsymbol {\Phi}_{\mathbf {q}_{2}^{B}}^{2}}^{T}\boldsymbol { \lambda}_{2}=\mathbf {Q}_{2}^{B}. $$
(53)

The objective of the algorithm at the position level is to find relations, which describe articulated body C (Fig. 3) in the form:

$$ \mathbf {M}_{11}^{C}\Delta{ \mathbf {q}}_{1}^{C}+ \mathbf {M}_{12}^{C}\Delta{ \mathbf {q}}_{2}^{C}+ {\boldsymbol {\Phi}_{\mathbf {q}_{1}^{C}}^{1}}^{T}\boldsymbol { \lambda}_{1}=\mathbf {Q}_{1}^{C}, $$
(54)
$$ \mathbf {M}_{21}^{C}\Delta{ \mathbf {q}}_{1}^{C}+ \mathbf {M}_{22}^{C}\Delta{ \mathbf {q}}_{2}^{C}+ {\boldsymbol {\Phi}_{\mathbf {q}_{2}^{C}}^{2}}^{T}\boldsymbol { \lambda}_{2}=\mathbf {Q}_{2}^{C}. $$
(55)

Lagrange multipliers between sets of bodies A and B can be evaluated using the following iterative scheme (see Eq. (100) in the Appendix):

(56)

Relations (50)–(56) take on the same form of Eqs. (11)–(17). Consistently, the assembly phase can be performed by using relations (27)–(32). The matrix coefficients (27)–(30) are computed once per integration step and are exploited in the velocity projections as well as in the process of acceleration evaluation. On the other hand vector quantities \(\mathbf {Q}_{i}^{A}\), \(\mathbf {Q}_{i}^{B}\) for i=1,2 in Eqs. (31)–(32) are computed in each iteration. The iterative scheme is continued until the stop criterion is met, which can be formulated as ∥Δq∥<ϵ p , where ϵ p is the user specified tolerance.

3.3 Projections in velocities

Similarly as at the position level, the numerical integration procedure yields velocities \(\dot{\mathbf {q}}_{*}\), which may not satisfy velocity constraint equations with the desired accuracy. The mass-orthogonal velocity projections to the constraint manifold help to improve numerical accuracy at this level. Let us consider the system of two rigid bodies, depicted in Fig. 2. The projections in velocities can be written in the following form [10, 27] (see Eq. (104) in the Appendix):

(57)
(58)

where vectors λ (with and without subscripts or superscripts) correspond to the process of constrained minimization of the functional \(V=\frac{1}{2}(\dot{\mathbf {q}}-\dot{\mathbf {q}}_{*})^{T}\mathbf {M}(\dot{\mathbf {q}}-\dot{\mathbf {q}}_{*})\) subjected to velocity constraint equations \(\dot{\boldsymbol {\Phi}}(\mathbf {q},\dot{\mathbf {q}},t)=\boldsymbol {0}\). The constraint equations between body A and B and Euler parameter normalization constraints at the velocity level can be written as follows:

(59)
(60)

The Lagrange multipliers at the velocity level can be approximated as (see Eq. (110) in the Appendix):

(61)
(62)
(63)

where Lagrange multipliers λ with the asterisk sign are evaluated in previous iteration. We assume λ ∗=0, \({\lambda}^{N*}_{A}=0\), \({\lambda}^{N*}_{B}=0\) for the initial iteration. Inserting Eqs. (61), (62), and (63) into (57), (58) yields

(64)
(65)

Equations (64) and (65) form a basis for further derivations. Again, we can write the generalized relations for the system of articulated bodies as shown in Fig. 3, which enable to correct all perturbed velocities:

(66)
(67)

and

(68)
(69)

The objective of the algorithm for mass-orthogonal projections is to find relations describing articulated body C (Fig. 3) in the form:

$$ \mathbf {M}_{11}^{C}\dot{\mathbf {q}}_{1}^{C}+ \mathbf {M}_{12}^{C}\dot{\mathbf {q}}_{2}^{C}+ {\boldsymbol {\Phi}_{\mathbf {q}_{1}^{C}}^{1}}^{T}\boldsymbol { \lambda}_{1}=\mathbf {Q}_{1}^{C}, $$
(70)
$$ \mathbf {M}_{21}^{C}\dot{\mathbf {q}}_{1}^{C}+ \mathbf {M}_{22}^{C}\dot{\mathbf {q}}_{2}^{C}+ {\boldsymbol {\Phi}_{\mathbf {q}_{2}^{C}}^{2}}^{T}\boldsymbol { \lambda}_{2}=\mathbf {Q}_{2}^{C}. $$
(71)

The Lagrange multipliers associated with the joint between sets of bodies A and B can be approximated as follows (see Eq. (110) in the Appendix):

$$ \boldsymbol {\lambda}=\boldsymbol {\lambda}^{*}+ \boldsymbol {\upalpha}\bigl(\boldsymbol { \Phi}_{\mathbf {q}_{2}^{A}}\dot{\mathbf {q}}_{2}^{A}+ \boldsymbol { \Phi}_{\mathbf {q}_{1}^{B}}\dot{\mathbf {q}}_{1}^{B}+\boldsymbol { \Phi}^{AB}_{t}\bigr). $$
(72)

The relations (66)–(72) are of the same structure as Eqs. (11)–(17). The matrix coefficients \(\mathbf {M}_{ij}^{A}\), \(\mathbf {M}_{ij}^{B}\) for i,j=1,2 are computed earlier in the process of projections in positions, whereas vector quantities \(\mathbf {Q}_{i}^{A}\), \(\mathbf {Q}_{i}^{B}\) for i=1,2 are evaluated in each iteration as a function of corrected velocities. The projections in velocities are continued until the specified convergence conditions are met, e.g., \(\|\dot{\mathbf {q}}^{(i+1)}-\dot{\mathbf {q}}^{(i)}\|<\epsilon_{v}\), where ϵ v is the user specified tolerance.

The mass-orthogonal projections in positions and velocities can be performed at each time step to obtain a set of values, which satisfy constraints equations within the user specified tolerance. Afterward, the corrected state variables are used to evaluate accelerations according to the divide and conquer scheme described in Sect. 2. The matrix coefficients M ij for i,j=1,2 from Eqs. (27)–(30) do not need to be reevaluated at this computational stage, because they are computed earlier in the process of position projections. The vector quantities Q i for i=1,2 from Eqs. (31), (32) are computed as a function of corrected state variables. If the projections are performed at each time step, the choice of parameters Ω and μ is irrelevant. They may be set to zero, because the position and velocity constraint equations are satisfied after the projections to the constraint manifold.

4 Numerical examples

4.1 Introduction

This section presents some results of the numerical experiments, which are performed to prove the correctness of the developed formulations as well as indicate some of its features. All of the test cases are simulated with intent of gathering characteristics of the parallel divide and conquer algorithm without and with mass-orthogonal projections. The comparisons are made with respect to accuracy and robustness of the formulations. All of the test cases are systems with closed kinematic loops and they are modeled as spatial mechanisms with redundant constraints, which may undergo singular configurations. Apart from the numerical issues, the ways of modeling MBS with closed kinematic chains are demonstrated and generalized.

The test cases are implemented in Matlab in double precision arithmetic, with standard ode45 integration procedure [40]. The absolute and relative tolerances are set to 10−6. All bodies are modeled as rigid interconnected via revolute joints only. The characteristic length of each body in the system is a=0.2 m, with masses m i =1 kg and inertia matrices equal to \(\mathbf{J}'_{i}=\operatorname{diag}(0.25)~\mathrm{kg\,m}^{2}\) with respect to the local reference frames (x i ,y i ,z i ) with the origin located at the centers of masses of bodies. It is assumed that the penalty factor is set to \(\boldsymbol {\upalpha}=\operatorname{diag}(10^{6})\), whereas other matrix coefficients, if needed, are \(\boldsymbol {\upmu}=\operatorname{diag}(1.0)\), \(\boldsymbol {\Omega}=\operatorname{diag}(1.0)\). The maximum number of iterations is limited to 10 at position, velocity and acceleration level, and simultaneously user specified tolerances are chosen to be ϵ p =10−14, ϵ v =10−12 and ϵ a =10−10, respectively. For each test multibody systems 10 second simulations are performed, with the mechanisms released from the initial state shown in figures under gravity forces.

4.2 Single kinematic loop

Consider the five-bar mechanism as shown in Fig. 4. The system is a representative of multibody systems with closed kinematic chains. Bodies 1 and 4 are connected to nonmovable base 0 to create a kinematic loop. All of the joints are revolute, with the axes of revolution perpendicular to the plane of the motion (page). From Grubler’s formula, it appears that the mobility of this spatial mechanism is w=6⋅4−5⋅5=−1, whereas in fact the system possess two degrees of freedom. Thus, three redundant constraint are imposed on the system. This situation implicates the permanent row rank deficiency of the Jacobian matrix. Moreover, the five-bar mechanism may undergo singular configurations as shown in Fig. 4, at that time the Jacobian matrix temporarily loses its current rank.

Fig. 4
figure 4

Five-bar mechanism, its singular configuration, and the binary tree associated with computations

Full size image

At the initial instant, the Cartesian coordinates of the points associated with axes of revolution in joints are located at the apexes of the pentagon and initial velocities are set to zero. After the assembly phase, the resulting equations of motion associated with the root node of the binary tree depicted in Fig. 4 can be expressed as follows:

(73)
(74)

The Lagrange multipliers λ 1 and λ 5 correspond to constraint forces in first and fifth joint. These quantities can be approximated as follows:

$$ \boldsymbol {\lambda}_{1}=\boldsymbol {\lambda}_{1}^{*}+\boldsymbol { \upalpha}\bigl(\boldsymbol {\Phi}_{\mathbf {q}_{1}}^{1}\ddot{\mathbf {q}}_{1}+ \overline{\boldsymbol {\gamma}}_{01}\bigr), $$
(75)
$$ \boldsymbol {\lambda}_{5}=\boldsymbol {\lambda}_{5}^{*}+\boldsymbol { \upalpha}\bigl(\boldsymbol {\Phi}_{\mathbf {q}_{4}}^{5}\ddot{\mathbf {q}}_{4}+ \overline{\boldsymbol {\gamma}}_{04}\bigr). $$
(76)

Inserting Eqs. (75), (76) into (73), (74), we obtain the linear system of equations with respect to accelerations of bodies 1 and 4:

(77)

It should be emphasized that the matrix coefficients in Eq. (77) are symmetric and positive definite even in the case, when Jacobian matrices are rank deficient (permanently or temporarily). In addition, there is a relation \(\mathbf {M}_{12}^{1-4}=(\mathbf {M}_{21}^{1-4})^{T}\), which can be used for improving computational efficiency. After evaluating \(\ddot{\mathbf {q}}_{1}\), \(\ddot{\mathbf {q}}_{4}\) and Lagrange multipliers λ 1, λ 5, the disassembly phase is started to compute all of bodies’ accelerations and constraint forces in joints.

Figure 5 shows the results obtained from a 10 second simulation of the five-bar multibody system when moving under gravity forces. The motion of the mechanism is smooth, without abrupt changes in values of kinematic parameters, even when passing repeatedly through singular configurations. The same qualitative and quantitative results are obtained for DCA algorithm with projections.

Fig. 5
figure 5

Simulation results for the five-bar mechanism obtained by using DCA algorithm without projections

Full size image

Figure 6 presents the constraint violation errors at position, velocity, and acceleration levels with respect to time. As can be noticed, both formulations assure the stabilization of constraint equations. The DCA algorithm with mass-orthogonal projections, performed each time step, indicates better constraints satisfaction compared to the formulation without projections. However, the improvement in accuracy requires additional computational expense, which refers to the numerical cost of projections in positions and velocities.

Fig. 6
figure 6

Constraint errors in positions, velocities and accelerations for the five-bar mechanism

Full size image

The plots of the kinetic, potential, and total energy for the five-bar mechanism are shown in Fig. 7. Similarly, as in case of constraint violations, the DCA algorithm with projections indicates better properties. For this case, the total energy of the system is conserved more accurately compared to the DCA algorithm without projections.

Fig. 7
figure 7

Kinetic, potential, and total energy of the five-bar mechanism

Full size image

On the basis of obtained results, it is can be seen that the proposed algorithms behave well for dynamics simulation of closed loop multibody systems with redundant constraints, which may repeatedly pass through singular configurations. Violations in constraint equations are reduced considerably. The formulations demonstrate advantages over traditional methods for constraint imposition based on Lagrange multipliers approach that may fail completely in considered test cases.

4.3 Coupled kinematic loops

The approach for dynamics simulation of single kinematic loop systems presented in Sect. 4.2 can be generalized for mechanisms with many coupled kinematic loops. As a simple representative of the group of systems, let us consider the mechanism shown in Fig. 8 with two coupled kinematic loops. Body 3 is common both for upper and lower closed kinematic chains. The theoretical mobility of the mechanism is equal to w=6⋅8−5⋅10=−2. In fact the system possesses four degrees of freedom, i.e., six redundant constraints are imposed on the system.

Fig. 8
figure 8

Double loop mechanism and the binary tree associated with computations

Full size image

Initially, the Cartesian coordinates of the points associated with axes of revolution in joints are located at apexes of two pentagons coupled together as shown in Fig. 8. The velocities are set to zero at first instant. Let us consider the binary tree depicted in Fig. 8 in order to formulate the equations of motion of the mechanism with coupled loops. At first, the lower kinematic loop is taken into account (bodies 5 to 8). The objective of the transformation is to reduce lower kinematic loop and to couple resulting relations with equations of motion of body 3. After that operation, the upper kinematic loop (bodies 1 to 4) will be considered as a single kinematic loop and its treatment will be similar to that presented in Sect. 4.2. After the assembly phase, the equations of motion of the assembly associated with the lower kinematic loop can be written as

(78)
(79)

The accelerations of bodies 5 and 8 can be evaluated from the system of linear equations (78) and (79) in terms of constraint forces in joints 6 and 10:

(80)

On the other hand, the Lagrange multipliers associated with constraint forces in joint 6 and 10 can be approximated as follows:

$$ \boldsymbol {\lambda}_{6}=\boldsymbol {\lambda}_{6}^{*}+\boldsymbol { \upalpha}\bigl(\boldsymbol {\Phi}_{\mathbf {q}_{3}}^{6}\ddot{\mathbf {q}}_{3}+ \boldsymbol {\Phi}_{\mathbf {q}_{5}}^{6}\ddot{\mathbf {q}}_{5}+ \overline{\boldsymbol {\upgamma}}_{35}\bigr), $$
(81)
$$ \boldsymbol {\lambda}_{10}=\boldsymbol {\lambda}_{10}^{*}+\boldsymbol { \upalpha}\bigl(\boldsymbol {\Phi}_{\mathbf {q}_{3}}^{10}\ddot{\mathbf {q}}_{3}+ \boldsymbol {\Phi}_{\mathbf {q}_{8}}^{10}\ddot{\mathbf {q}}_{8}+ \overline{\boldsymbol {\upgamma}}_{38}\bigr)\mbox{ }. $$
(82)

Equations (81) and (82) can be rewritten in matrix form:

(83)

Inserting Eq. (80) into (83), we obtain

(84)

where \(\mathbf {C}=(\frac{1}{\alpha} \mathbf {I}+\boldsymbol {\Phi}_{\mathbf {q}}\mathbf {M}^{-1}\boldsymbol {\Phi}_{\mathbf {q}}^{T})^{-1}\) is symmetric and positive definite matrix. It can be seen that Eq. (84) connects Lagrange multipliers λ 6, λ 10 with accelerations of body 3. Let us consider equations of motion for body 3:

(85)

Inserting Eq. (84) into (85), we obtain finally

$$ \overline{\mathbf {M}}_{3}\ddot{\mathbf {q}}_{3} +{\boldsymbol { \Phi}_{\mathbf {q}_{3}}^{3}}^{T}\boldsymbol {\lambda}_{3} +{\boldsymbol {\Phi}_{\mathbf {q}_{3}}^{4}}^{T}\boldsymbol { \lambda}_{4} +{\boldsymbol {\Phi}_{\mathbf {q}_{3}}^{N}}^{T}{ \lambda}_{3}^{N} =\overline{\mathbf {Q}}_{3} , $$
(86)

where \(\overline{\mathbf {M}}_{3}=\mathbf {M}_{3}+\boldsymbol {\Psi}_{\mathbf {q}}^{T}\mathbf {C}\boldsymbol {\Psi}_{\mathbf {q}}\) and

$$\overline{\mathbf {Q}}_{3}=\mathbf {Q}_{3}-\boldsymbol {\Psi}_{\mathbf {q}}^{T}\mathbf {C} \left(\frac{1}{\alpha} \left [\begin{array}{c} \boldsymbol {\lambda}_{6}^{*} \\ \boldsymbol {\lambda}_{10}^{*} \end{array} \right ]+\boldsymbol {\Phi}_{\mathbf {q}}\mathbf {M}^{-1}\mathbf {Q}+\overline{\boldsymbol {\gamma}}\right ). $$

It should be emphasized that Eq. (86) expresses dynamics of body 3 as well as motion of lower kinematic loop. The operation of reduction of lower kinematic loop enables to treat upper loop as single closed kinematic chain. Therefore, it is possible to apply the similar formulation as described in Sect. 4.2 to that case.

Figure 9 shows the results obtained from dynamics simulation of the double loop mechanism. As in the case of the five-bar mechanism, the motion is smooth without violent changes in kinematic parameters. Constraint errors in positions, velocities, and accelerations shown in Fig. 10 are significantly reduced even up to machine precision in case the DCA algorithm with projections is applied. Also, the total energy of the system depicted in Fig. 11 is well conserved being superior for the DCA with mass-orthogonal projections.

Fig. 9
figure 9

Simulation results for the double loop mechanism obtained by using DCA algorithm without projections

Full size image
Fig. 10
figure 10

Constraint errors in positions, velocities, and accelerations for the double loop mechanism

Full size image
Fig. 11
figure 11

Kinetic, potential, and total energy of the double loop mechanism

Full size image

4.4 Discussion

The constraint equations for multibody systems considered in the paper are imposed at the acceleration level. The solution of mixed differential equations of motion together with such algebraic relations suffers from accumulation of constraint errors. Constraint imposition at the acceleration level may lead to substantial violation of the position and velocity constraint equations and, in consequence, unacceptable results for a given simulation. The problem may be solved by introducing constraint stabilization techniques. Special formulations have to be taken into account when dealing with redundant constraints in multibody systems and some peculiarities of the methodologies should be concerned in modeling of mechanisms passing through singular configurations.

The first variant of the formulation presented in the paper combines the divide and conquer algorithm with the augmented Lagrangian method. Lagrange multipliers are approximated by the weighted sum of constraint equations and its two derivatives. The algorithm is robust in the case of modeling systems with redundant constraints, and may handle singular configurations. The second variant maintains all the advantages of the former method and yields better constraints fulfillment by applying mass-orthogonal projections to the constraint manifold at position and velocity level. This algorithm appears to be much more accurate than the regular DCA with augmented Lagrangian method but at the expense of computational burden associated with error corrections.

In the context of DCA based methods, the singularities may be overcome by different approaches. Featherstone in his original work [16] includes the capability of dealing with closed loop systems. For the most general case, the kinematic loops are treated by using generalized inverses and the loop constraint equations are made stable with the add of well-known Baumgarte technique [8]. On the other hand, Mukherjee and Anderson [32] developed a noniterative divide and conquer algorithm for forward dynamics of MBS with single and coupled loops that incorporates orthogonal complements of the joint motion subspace. This method indicates well constraint satisfaction without necessity of applying additional constraint stabilization techniques. In the paper, the singular configurations are overcome by introducing the approximation of Lagrange multipliers based on the augmented Lagrangian method. Due to that fact, the key matrices in the algorithms are nonsingular even when Jacobian matrices lose permanently or exceptionally their rank. The proposed algorithms are inherently iterative. Therefore, some additional computational burden is expected for the first and second variant of the methodology as compared to mentioned counterparts.

The main computational load for the DCA algorithm combined with the augmented Lagrangian formulation is associated with the first iteration. The process of assembly requires the calculation of coefficients according to Eqs. (27)–(32). Taking into account the boundary conditions presented in Sect. 2.3, the disassembly phase is started by exploiting Eqs. (21), (23), and (17). The computational burden is significantly reduced each next iteration, because the matrices M ij for i,j=1,2 are constant in the iterative process. Vectors Q i for i=1,2 and accelerations are the only quantities that should be reevaluated each iteration. Looking carefully at the recursive formulae, one can find that the efficiency can be further improved by computing only these values, which are dependent on the Lagrange multipliers and accelerations from the previous iteration. This remark allows to avoid expensive matrix multiplications and inversions and, in consequence, diminish the overall numerical cost of the formulation to the extent possible.

The additional computational burden is expected for the second formulation proposed in this work. The added load is associated with the mass-orthogonal projections to the constraint manifold. Similar conclusions may be drawn for the error correction stage at position and velocity level compared to the regular algorithm. The matrix coefficients in the form of M ij for i,j=1,2 are evaluated at the beginning of the projection at the position level. During the iterative process, they are constant, and then are once reevaluated before the start of the velocity projection scheme. It should be noted that these values remain also constant at the velocity and acceleration level. Vectors Q i for i=1,2 and demanded unknowns (positions, velocities, or accelerations) are the only quantities that are altered each iteration. The experience of the authors demonstrated that the penalty factors ranging from 105 to 107 give a good convergence rate at each level of computations. The number of iterations is dependent on the user specified tolerances but usually at most 4 iterations are sufficient to obtain reasonable solutions for considered mechanisms.

In conclusion, the computational complexity of both variants considered in the work can be approximated as O(kn) sequentially and becomes \(O(k\operatorname{log}_{2}n)\) for parallel implementations on O(n) processors, where k is the number of iterations. A more detailed and quantitative discussion is needed to estimate the numerical cost associated with the proposed algorithms compared to other approaches available in the literature. These issues are areas of ongoing work of the authors and is planned to be addressed in a forthcoming publications.

5 Conclusions

In this paper, new formulations for application to general multibody system dynamics have been developed, verified, and compared. Obtained iterative algorithms are linear, when considered sequentially and achieve logarithmic complexity for parallel computing. Developed methods treat tree topology systems, and general systems which contain kinematic closed loops in a uniform manner and can handle situations, when constraint Jacobian matrices lose its rank. The methods based on augmented Lagrangian formulations with projections ensure appropriate numerical properties. Numerical results of the test cases indicate good accuracy performance dependent on the expense put in the iterative refinement of constraint equations. The formulations are robust in case of analyzing systems with redundant constraints, and which may enter singular configurations. The developed formulations can be extended for analyzing dynamics of complex systems with unilateral constraints, which are areas of forthcoming research for the authors.