1 Introduction

Tropical cyclones (TCs), that often develop in the western North Pacific region, are the most destructive natural phenomena in China. Offshore and landfalling TCs may induce heavy precipitation, storm surge, and wind gusts, which can lead to enormous loss of lives and personal properties (Konrad et al. 2009; Li et al. 2015). Climatologically, TC rainfall accounts for approximately 20–40% of the total rainfall over southeast China during boreal summer, and the contribution can even reach 50% for some of the coastal provinces (Li and Zhou 2015). Guangxi Zhuang Autonomous Region (Guangxi) is the southernmost province in mainland China, with the South China Sea adjacent on its south. TCs that form in or move into the north of 19°N and west of 112°E are termed the TCs affecting Guangxi. According to the statistical data developed by the Guangxi Meteorological Bureau, a total of 286 TCs affect Guangxi during the period of 1949–2001, with an average of 5.5 TCs per year. The maximum number of TCs affecting Guangxi was nine in 1952, 1961, 1971, and 1974 (Guangxi Climate 2007). From 2002 to 2015, there were 67 TCs affecting Guangxi, with the maximum number being eight TCs in 2013. The continuous torrential rain associated with a TC often caused flood, landslide, or debris flow, leading to serious damages to Guangxi. Supertyphoon Rammasun in 2014, the strongest typhoon to hit South China in four decades, made landfall three times in China. The average wind speeds near the TC center were more than 60 ms−1. Rammasun made its third landfall in Fangchenggang City of Guangxi on July 19, 2014 (Xinhuanet News 2014a, b). Under the spell of the typhoon, Guangxi has reported a direct economic loss of 1.63 billion yuan (261.63 million US dollars) by the date of July 20, 2014 (Xinhuanet News 2014a, b). For such a landfalling TC as Rammasun, it is very important to issue timely and accurate TC warnings for the local residents to evacuate or to be prepared for the coming disaster. Therefore, quantitative forecasts of rainfall caused by TCs affecting Guangxi are important and required.

High-resolution numerical weather prediction (NWP) models hold promise for enhancing the accuracy of precipitation. In recent years, statistical and numerical approaches have been successfully applied to TC precipitation prediction. For the numerical approaches, to understand the complicated physical mechanisms that occur during typhoon attacks in China, some insightful real-case numerical studies have been undertaken. The rainfall process from Typhoon Haitang in 2005 was simulated using the Weather Research and Forecasting (WRF) model and based on simulated outputs, and the cause of asymmetric distribution formation of rainfall associated with Typhoon Haitang was analyzed quantitatively (Yue 2009). Zhang et al. (2010) examined the prediction of the catastrophic rainfall and flooding event over Taiwan induced by Typhoon Morakot (2009) with a state-of-the-art numerical weather prediction model. A precipitation simulation associated with Typhoon Sinlaku using the fifth-generation Pennsylvania State University–National Center for Atmospheric Research Mesoscale Model (MM5) initialized diabatically with the Local Analysis and Prediction System (LAPS) was evaluated over the Taiwan area (Jian et al. 2003). Taniguchi et al. (2013) improved the high-resolution Global Satellite Mapping of Precipitation (GSMaP) product for Typhoon Morakot (2009) over Taiwan by using an orographic/nonorographic rainfall classification scheme. Marchok (2007) developed a scheme for validating quantitative precipitation forecasts for landfalling TCs, and the Global Forecast System (GFS) performed the best of all of the models for each of the categories. In weather forecast, the prediction of rainfall during TCs by statistical approaches has received much attention in recent years. Lee et al. (2006) developed a climatology model for typhoon rainfall, providing hourly rainfall at any station or any river basin for a given typhoon center. Lonfat et al. (2007) documented a new parametric hurricane rainfall prediction scheme, based on the rainfall climatology and persistence model (R-CLIPER) used operationally in the Atlantic Ocean basin to forecast rainfall accumulations. Using the skills of the artificial intelligence and machine learning, Wei (2012) presented two support vector machine (SVM)-based models for forecasting hourly precipitation during TC events. The two SVM-based models are the traditional Gaussian kernel SVMs and the advanced wavelet kernel SVMs. Lin and Chen (2005) developed a neural network with two hidden layers to forecast typhoon rainfall using eight typhoon characteristics. Li et al. (2015) proposed a nonparametric statistical method to predict short-term rainfall due to TCs in a coastal meteorological station. However, the physically based model is mathematically a highly complicated, nonlinear numerical model in space and time, and an accurate quantitative precipitation forecast for TC remains one of the most difficult tasks (Lee et al. 2006).

At present, as a new technique for weather forecast, artificial neural networks (ANNs) are effective at solving complex nonlinear problems and have been applied successfully in many disciplines (Kwong et al. 2012; Yip and Yau 2012). But artificial neural network (ANN) can get stuck in a poor local minimum of error surface; thus, the fuzzy algorithm is presented for overcoming this problem. Fuzzy systems, first proposed by Lotfi A. Zadeh (1965), can be used for solving a problem if there does not exist any mathematical model of the given problem, and it is characteristic of fuzzy reasoning to deal with high-order information. Compared with genetic algorithm and particle swarm optimization algorithm, fuzzy systems are simper and have quicker convergence speed when solving the complex nonlinear problem. In this paper, combining neural network with fuzzy systems, the resultant fuzzy neural network (FNN) can broaden the scope and capability of the neural network to process the precise information, fuzzy information, and other inaccurate information by blurring neurons.

On the other hand, manifold learning is a highly popular dimensionality reduction technique for high-dimensional data in recent years and is applied in pattern recognition, machine learning, and data mining (Huang and Jin 2013; Chen et al. 2008; Xu and Guo 2006). It is helpful in revealing the structural knowledge of high-dimensional data. Specifically, the locally linear embedding (LLE) algorithm is a representative of manifold learning approaches (Roweis and Saul 2000). It has emerged as a promising technique to reconstruct nonlinear low-dimensional manifold embedded in high-dimensional spaces, by which the high-dimensional data are visualized nicely. As a consequence, taking the western North Pacific TC precipitation affecting Guangxi as the prediction object and using FNN, a novel objective prediction method for TC precipitation is proposed, with a low-dimensional learning matrix for FNN being constructed using a combination of stepwise regression calculation and LLE nonlinear dimension reduction.

2 Principle behind and method for creating FNN–LLE prediction model

The principles of the FNN and LLE approaches are described below.

2.1 Fuzzy neural network

A fuzzy neural network (FNN) is a learning machine that finds the parameters of a fuzzy system (i.e., fuzzy sets and fuzzy rules) by exploiting approximation techniques from neural networks. Both neural networks and fuzzy systems have some things in common. They can be used for solving a problem (e.g., pattern recognition, regression, or density estimation) if there does not exist any mathematical model of the given problem (Kruse 2008). The fuzzy algorithm is simpler and better in the goodness of fit than are traditional optimization algorithms. Thereby, FNN is applied in many disciplines (Han et al. 2017; Si et al. 2017). However, in meteorology, in addition to the application of FNN in the cloud image recognition (Chen et al. 2005; Yu et al. 1996), FNN is only applied in TC intensity prediction (Huang et al. 2009) and precipitation prediction (Shi et al. 2009), and there is no research on FNN in TC precipitation prediction modeling. In this paper, an FNN method is proposed to forecast TC rainfall in Guangxi.

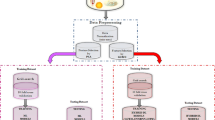
Compared to a common neural network, connection weights and propagation and activation functions of FNN differ a lot. An FNN is represented as a special four-layer feedforward neural network in this paper as it is shown in Fig. 1. The four-layer FNN is as follows: the input layer, the membership generation layer, the fuzzy inference layer, and the defuzzification output layer (Wang 1998), including fuzzy–fuzzy inference–defuzzification of the basic fuzzy systems. The number of nodes and weight of each layer can be preset according to the specific model used by the fuzzy systems. The sum of squares of errors is taken as the objective function in the network algorithm, and the gradient method is used to obtain the minimum value. The layers of FNN architecture are described as follows:

Fig. 1
figure 1

Architecture of a FNN

Full size image
  1. 1.

    The first layer: input layer. It corresponds to the input variables.

  2. 2.

    The second layer: membership generation layer. In this layer, the fuzzy sets are encoded for the input variables from the first layer, and the membership degree of the fuzzy sets is calculated by the membership function. Gaussian function is used as the membership function using the following expression:

    $$ \mu_{ij} (x_{i} ) = \exp \left[ { - \frac{{(x_{i} - a_{ij} )^{2} }}{{\sigma_{ij}^{2} }}} \right],\quad i = 1,2, \ldots \;n;\;j = 1,2, \ldots m $$
    (1)

    where \( \mu_{ij} \) is the jth membership function of \( x_{i} \); \( a_{ij} \) is the center of the jth membership function of \( x_{i} \); \( \sigma_{ij} \) is the width of the jth membership function of \( x_{i} \); n is the number of input variables; and m is the number of membership functions and the number of fuzzy rules of the system.

  3. 3.

    The third layer: fuzzy inference layer. The number of the nodes m represents the number of fuzzy rules. Each node represents the IF-part in fuzzy rules. The fuzzy membership degree of the jth output of the ith variable passing through the second layer is calculated. In fuzzy systems, the multiplication is used in the “and” operation, and the output of each node is the algebraic product of the all the input of the node.

    $$ \pi_{j} = \mu_{1j} \times \mu_{2j} \times \cdots \times \mu_{nj} = \prod\limits_{i = 1}^{n} {\mu_{ij} } ,\quad j = 1,2, \ldots m $$
    (2)
  4. 4.

    The fourth layer: defuzzification output layer. Each node of the layer represents an output variable, which is a superposition of all input signals and defined as:

    $$ \hat{y}_{i} = \omega_{1i} \pi_{1} + \omega_{2i} \pi_{2} + \cdots + \omega_{mi} \pi_{m} = \sum\limits_{j = 1}^{m} {\omega_{ji} \pi_{j} } $$
    (3)

    where \( \omega_{ji} \) is the weight from the jth fuzzy neuron to the ith output neuron (i = 1, 2,…, n; j = 1, 2,…, m).

FNN training is to adjust the fuzzy center \( a_{ij} \), width \( \sigma_{ij} \) of the membership function, and the connection weights \( \omega_{ji} \) of defuzzification output layer by means of error back-propagation method in this paper, which is different from a common back-propagation neural network (BPNN).

The total error in the performance of the network can be computed by comparing the actual and desired output vectors for every case. The total error, E, is defined as:

$$ E = \frac{1}{2}\sum\limits_{i = 1}^{n} {(\hat{y}_{i} - y_{i} } )^{2} $$
(4)

where \( y_{i} \) is the desired output; and\( \hat{y}_{i} \) is the actual output. To minimize E by gradient descent, it is necessary to compute the partial derivative of E with respect to each weight in the network. The learning rules of the fuzzy center \( a_{ij} \) and width \( \sigma_{ij} \) of the membership function, and the connection weights \( \omega_{ji} \) of the defuzzification output layer are as follows:

$$ a_{ij} (t + 1) = a_{ij} (t) - \alpha \frac{\partial E}{{\partial a_{ij} }} $$
(5)
$$ \sigma_{ij} (t + 1) = \sigma_{ij} (t) - \alpha \frac{\partial E}{{\partial \sigma_{ij} }} $$
(6)
$$ \omega_{j} (t + 1) = \omega_{j} (t) - \alpha \frac{\partial E}{{\partial \omega_{j} }} $$
(7)

where α is the learning factor (0 < α < 1) and t is the number of neural network training times (1 ≤ t ≤ N, N is the maximum number of training times). Using the derivation rule of the composite function and Eq. (4), the updating formula of the membership function parameters and the weight is as follows:

$$ a_{ij} (t + 1) = a_{ij} (t) - 2\alpha (\hat{y}_{i} - y_{i} )\omega_{j} \times \prod\limits_{i = 1}^{n} {\mu_{ij} } \times (x_{i} - a_{ij} )/\sigma_{ij}^{2} $$
(8)
$$ \sigma_{ij} (t + 1) = \sigma_{ij} (t) - 2\alpha (\hat{y}_{i} - y_{i} )\omega_{j} \times \prod\limits_{i = 1}^{n} {\mu_{ij} } \times (x_{i} - a_{ij} )^{2} /\sigma_{ij}^{3} $$
(9)
$$ \omega_{j} (t + 1) = \omega_{j} (t) - \alpha (\hat{y}_{i} - y_{i} )\pi_{j} $$
(10)

Therefore, the learning algorithm of this FNN can be summed up as follows:

  1. 1.

    Set the number of fuzzy rules m, the learning factor α, the global convergence error e, and the maximum number of training times N.

  2. 2.

    Randomly generate the connection weights ω, the fuzzy center a, and width σ of the membership function at initial time.

  3. 3.

    Adjust parameters and weights by error back-propagation method. The output of the second, third, and fourth layers of the FNN are calculated in turn.

  4. 4.

    Calculate the output error E of the model between the actual and desired output vectors in Eq. (4).

  5. 5.

    Loop to step 3 until a criterion is met, usually a sufficiently good fitness (E < e) or maximum number of iterations (N).

Because the operating mechanism has fuzzy features, FNN significantly enhanced the fault-tolerant ability. The learning time, training time, and calculation accuracy of FNN are superior to that of the conventional neural network method. Figure 2 shows the procedures of FNN prediction modeling.

Fig. 2
figure 2

Flowchart for FNN prediction modeling

Full size image

2.2 Locally linear embedding algorithm

From the principle introduction of FNN model in the last section, it reveals that FNN model is unable to provide a method regarding how to select good factors as model input for TC precipitation prediction. In the current operational statistical forecast for TC precipitation, with the maturing of observation conditions, it becomes easy to obtain a large amount of physical factors of numerical prediction products, and the number of selected physical factors by correlation calculation ranges from 80 to 100, from which only about 10 physical predictors are screened out as statistical model input for predicting TC precipitation using stepwise regression method. The useful prediction information of the residual 70–90 predictors are discarded, without being further utilized. To solve this problem, in this paper, all physical predictors are first screened out by means of stepwise regression method, and then the residual high-dimensional predictor data are represented by an efficient low-dimensional architecture using the nonlinear Locally Linear Embedding (LLE) algorithm (Roweis and Saul 2000). As a result, in order to fully excavate the useful information, this paper introduces a novel data mining technique by employing both a stepwise regression method and an LLE algorithm for constructing FNN model input from all physical predictors.

LLE algorithm is an unsupervised learning algorithm that computes low-dimensional, neighbor-hood-preserving embeddings of high-dimensional inputs. Unlike clustering methods for local dimensionality reduction, LLE maps its inputs into a single global coordinate system of lower dimensionality, and its optimizations do not involve local minima. By exploiting the local symmetries of linear reconstructions, LLE is able to learn the global structure of nonlinear manifolds. Additionally, unlike LLE, projections of the data by principal component analysis (PCA) or classical multidimensional scaling (MDS) map faraway data points to nearby points in the plane, failing to identify the underlying structure of the manifold. LLE recovers global nonlinear structure from locally linear fits (Roweis and Saul 2000). The use of the LLE dimension reduction for nonlinear meteorological data is a new attempt. The complete LLE algorithm has three steps (Roweis and Saul 2000).

Suppose the data consist of n real-valued vectors X = {X 1, X 2,…, X N }, each of dimensionality D, sampled from some underlying manifold.

  1. 1.

    Select neighbors. Assign neighbors to each data point X i , for example, by using the k nearest neighbors.

  2. 2.

    Reconstruct with linear weights. Compute the weights W ij that best linearly reconstruct X i from its neighbors, solving the constrained least-squares problem in the cost function Eq. (11).

    $$ \hbox{min} \varepsilon (W) = \sum\limits_{i = 1}^{n} {\left\| {X_{i} - \sum\limits_{j = 1}^{k} {W_{ij} X_{j} } } \right\|}^{2} $$
    (11)

    where the weights W ij summarize the contribution of the jth data point to the ith reconstruction. To compute the weights W ij , we minimize the cost function subject to two constraints: first, that each data point X i is reconstructed only from its neighbors, enforcing W ij  = 0 if X j does not belong to the set of neighbors of X i ; second, that the rows of the weight matrix sum to one: \( \sum\nolimits_{j = 1}^{k} {W_{ij} } = 1. \)

  3. 3.

    Map to embedded coordinates. Compute the low-dimensional embedding vectors Y i best reconstructed by W ij , minimizing Eq. (12) by finding the smallest eigenmodes of the sparse symmetric matrix in Eq. (13). Although the weights W ij and vectors Y i are computed by methods in linear algebra, the constraint that points are only reconstructed from neighbors can result in highly nonlinear embeddings.

    $$ \hbox{min} \varPhi (Y) = \sum\limits_{i = 1}^{n} {\left\| {Y_{i} - \sum\limits_{j = 1}^{k} {W_{ij} Y_{j} } } \right\|}^{2} $$
    (12)
    $$ M_{ij} = \delta_{ij} - W_{ij} - W_{ji} + \sum\limits_{k = 1}^{n} {W_{ki} W_{kj} } $$
    (13)

    where \( \delta_{ij} = 1 \) if i = j and 0 otherwise; \( \sum\nolimits_{i = 1}^{n} Y = 0 \) and \( \frac{1}{n}YY^{T} = I \), I is the d × d identity matrix. The optimal embedding, up to a global rotation of the embedding space, is found by computing the bottom d + 1 eigenvectors of the matrix (13). Note that the matrix M can be stored and manipulated as the sparse matrix (I − W)T(I − W), giving substantial computational savings for large values of n. Moreover, its bottom d + 1 eigenvectors (those corresponding to its smallest d + 1 eigenvalues) can be found efficiently without performing a full matrix diagonalization.

Accordingly, LLE algorithm provides a simple way to analyze and manipulate high-dimensional observations based on the estimation of underlying eigenfunctions. The free parameters are nearest neighbor number k and embedded space dimension d.

3 Study area and data

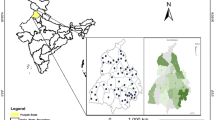
This study focuses on Guangxi, China, to explore the potential rainfall caused by TCs. Thirty-six years of the western North Pacific TC data were taken from the “CMA-STI Best Track Dataset for Tropical Cyclones over the western North Pacific” obtained from China typhoon network (Ying et al. 2014) from 1980 to 2015. The TC data are observed at intervals of 6 h, at 02, 08, 14, and 20 h (Beijing time, the same below), starting from the first instant that the TC moved into the sea area 0–45.0°N west of 180°E or from when a cyclone developed into a TC in the area. TCs in this paper refer to typhoons that formed in or moved into the north of 19°N and west of 112°E in Guangxi warning area (see Fig. 3). Guangxi is located in the southwest of China’s coastal areas, with the latitude from 20°54′ to 26°26′ and longitude from 104°29′ to 112°04′ (Guangxi Climate 2007) (see Fig. 3).

Fig. 3
figure 3

Location of study site for Guangxi, China

Full size image

Thirty-six years of daily rainfall data from Guangxi Meteorological Service, China, spanning 1980 to 2015 were taken in this paper. The accumulative daily rainfall is from 20:00 (Beijing Time, or BT, the same below) of the previous day to 20:00 BT of the current day at 89 stations covering Guangxi mainland and Weizhou Island for model development. The rainfall sample was when the TCs were in Guangxi warning line: north of 19°N and west of 112°E. Considering that if the TCs were not numbered or move out of the Guangxi warning line, their residual clouds may still cause rainfall. Hence, the rainfall sample is extended 2 days for each TC. For example, if a TC affecting Guangxi on date A 1, A 2,…, A t , then 2 days will be added after A t , that is, the date A 1, A 2,…,A t , A t+1, A t+2 is for model development. According to the statistical analysis, a total of 632 daily samples were available as the modeling samples from 1980 to 2010 data and 94 daily samples as the independent samples from 2011 to 2015 for successive prediction experiments.

In order to analyze the large-scale circulation of TC activity, the physical quantities of numerical weather prediction (NWP) were selected from the US National Centers for Environmental Prediction (NCEP)/National Center for Atmospheric Research (NCAR) (Kalnay et al. 1996), including the temperature field, wind field, geopotential height field, specific humidity field, and vertical velocity field. The resolution of the physical quantities is 2.5° × 2.5°; the time is 36 years from 1980 to 2015; the range is a total of 45 grid points from 17.5°N to 27.5°N in latitude and from 100°E to 120°E in longitude.

Considering the fact that weather satellites were put into service in 1965, the number of stations in each year is not stable due to gradually building stations in Guangxi. Here, the initial year was chosen as 1980 to ensure the accuracy of rainfall data in weather stations. The 89 weather stations in Guangxi meet the following conditions: (1) all 89 stations existed during 1980–2015; (2) complete rainfall record at 20–20 BT when TCs affect Guangxi; and (3) the 89 stations distributed uniformly over 14 cities in Guangxi. The locations of these 89 stations are illustrated in Fig. 4.

Fig. 4
figure 4

Distribution of the 89 stations in Guangxi, China, (+) used in the FNN–LLE model for TC precipitation prediction

Full size image

4 Models and applications

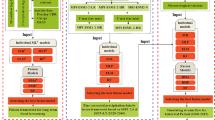
In this section, FNN–LLE model, stepwise regression method (SRM), and interpolation method by interpolating the fine-mesh data of the European Centre for Medium-Range Weather Forecasts (ECMWF), are implemented for forecasting precipitation estimates during TC attacks.

4.1 Predictand

During the 36-year period spanning 1980–2015, the tracks of TCs affecting Guangxi are mostly westerly. Some stations had heavy rainstorm even extraordinary rainstorm where TC strongly impacts, while some stations had general precipitation where TC weakly impacts. For example, for the TC Rainbow (2015), Guangxi precipitation map is shown in Fig. 5 on October 5, 2015. Results show that rainstorms mostly fell in the eastern and southeastern Guangxi, basically more than 100 mm, where the maximum precipitation is in Jinxiu station, reaching 335.5 mm; the second is Pingnan station with 216.8 mm; while the precipitation of the stations in the western Guangxi, such as Xilin, Daxin, Pingxiang, Longzhou, and so on, were less than 10 mm. Therefore, 89 forecast models have been established for the 89 stations in Guangxi, respectively, based on the correlation between the TC precipitation predictand and the physical quantities of NWP.

Fig. 5
figure 5

Precipitation affected by TC Rainbow on October 5, 2015, in Guangxi, China

Full size image

4.2 Samples

By statistical analysis, this study included a total of 172 TC events affecting Guangxi (entered the north of 19° and west of 112°, see Fig. 1) over the past 36 years (1980–2015), as shown in Table 1. The date of each TC were extended 2 days after TC not being numbered since there is likely to influence rainfall at 89 stations, so there were 726 precipitation samples in 172 TCs. Concurrently, precipitation samples from 1980 to 2010 were used in the prediction modeling, and those from 2011 to 2015, were used as independent samples in prediction testing. The data from 1980 to 2010 contain 150 relevant typhoons, with 632 corresponding TC precipitation samples for prediction modeling, and the data from 2011 to 2015 include 22 typhoons and 94 independent samples (see Table 2).

Table 1 TC events studied
Full size table
Table 2 Number of TCs during 1980–2015 affecting Guangxi and sample sizes of prediction modeling and independent samples for TC precipitation prediction experiments at 89 stations in Guangxi, China
Full size table

4.3 Potential predictors

The selection of predictors for precipitation forecasting is an important issue in statistical forecast methods. Generally speaking, rainfall requires a certain degree of water vapor and power, thermal conditions. Thereby, the physical quantities of the global reanalysis data of NCEP/NCAR were taken as the factors for TC precipitation prediction in this paper, and 21 precipitation physical quantities were extracted, including omega (vertical velocity) field, specific humidity field, geopotential height field, and physical quantity index for precipitation such as K index, ky index, SI index, and so on (see Table 3). The resolution of the physical quantities is 2.5° × 2.5°; the time is 36 years from 1980 to 2015. The range is latitude of 17.5°N–27.5°N, longitude of 100°E–120°E, and a total of 45 grid points as the scope of the correlation calculation. By calculating the correlation coefficient of each grid point with the predictand (daily TC precipitation of 89 stations), a predictor area was selected where the number of neighboring grid points with these correlations absolutely above 0.20 (98% significance test) was greater than 50. At each predictor area, if the grid points’ correlations were absolutely above 0.30 (99% significance test), they were picked out as the computational grid point for the predictor, which is to further enhance the stability and high correlativity of predictors.

Table 3 Factors for precipitation prediction
Full size table

Following this preliminary selection, a set of about 80–100 potential physical quantities predictors was chosen for TC precipitation estimation in this paper (Table omitted). There is a complex correlation among these factors. If these factors are directly used as the FNN model input, it will easily lead to the complexity of network learning, over-fitting, and other issues (Jin et al. 2004). Therefore, for these primary predictors, several rainfall forecasting factors with high correlation and useful information were extracted, by using the predictor information data mining techniques combining LLE algorithm feature extraction with stepwise regression calculation. Then, the FNN was used to simulate the prediction of TC precipitation at station 89 in Guangxi. Table 4 illustrates the input dimension of FNN model in the first TC precipitation prediction modeling for forecasting the first independent sample for several stations. As space is limited, it is unnecessary to give the detail of model input for all 89 stations here.

Table 4 Number of predictors for the first TC precipitation prediction modeling for several stations
Full size table

4.4 Construction of models

  1. 1.

    FNN–LLE model

    When neural network and fuzzy systems are applied in prediction modeling, they are incapable of providing a method for selecting good factors from potential physical quantities factors as model input. It is very important to choose the key factors for avoiding the interference of the bad factors and to control the model input for avoiding “fuzzy rule explosion” caused by a large input matrix. Stepwise regression method (Lund 1971) is implemented for screening out factors from potential physical quantities factors for TC precipitation prediction, and it is a widely used forecasting scheme in statistical prediction. Meanwhile, there is a nonlinear relationship between the predictand (TC precipitation) and predictor. Consequently, to utilize the prediction information of all potential physical quantities factors and construct reasonable learning matrix for FNN model input, a new approach is performed in this paper.

    Taking the TC precipitation forecast of Beihai station predictand (Beihai is near the Beibu Gulf and strongly influenced by TCs) and 86 primary physical quantities predictors as an example (Table 4), a stepwise regression procedure was applied for predictors selection, and 10 physical quantities predictors were chosen corresponding to F = 4. The remaining 76 physical quantities predictors were highly information-condensed, and system dimensionality reduced by implementing LLE algorithm, where the number of nearest neighbors is 15 and the embedded space dimension is 2 (Huang et al. 2014). Thus, the predictors entering FNN model are both two nonlinear LLE predictors and 10 stepwise regression predictors; a set of 12 predictors were used for TC precipitation forecast of Beihai station. In the fuzzy computation, the number of fuzzy rules was three. In the NN computation, the learning factor was 0.9; the network training error was 0.001; the training time was 200; and the learning and momentum factors were both 0.5. Therefore, the resultant FNN–LLE prediction model for TC precipitation prediction in Guangxi has been constructed.

    In order to be useful in an operational setting, the successive prediction method was employed in the experiments. In the TC precipitation forecast of 89 stations predictand, there are 632 modeling samples and 94 independent samples in the 89 stations in Guangxi. The first independent sample was predicted using 632 modeling samples (Table 2), the second using 633 modeling samples (632 modeling samples plus the first independent sample, which had become a known observation when the second independent sample was forecasted), and so on, until the last (94 h) independent sample was predicted using 725 modeling samples. In all successive predictions, all parameters of FNN and LLE were kept unchanged. Of course, in the forecast procedure, the current TC precipitation is removed from the modeling database. Moreover, the potential physical quantities factors were recalculated correlation coefficients with the predictand (TC precipitation) in each forecast, so were the stepwise regression predictors and the LLE dimension reduction calculation, to ensure comparability between independent sample predictions and actual operational predictions.

  2. 2.

    Interpolation method by ECMWF

    There are three commonly used interpolation methods by interpolating the fine-mesh data of the ECMWF to stations used in rainfall forecasting, including bilinear interpolation, cubic polynomial interpolation, and spline function interpolation, and these, the prediction capability of three interpolation methods, are almost the same (Zhao et al. 2014). Thereby, cubic polynomial interpolation by ECMWF was implemented for TC precipitation forecast at 89 stations in Guangxi over 1980–2015 in this paper.

  3. 3.

    Stepwise regression model

    For objective comparison and analysis, taking about 10 predictors from stepwise regression method for F = 4 in Table 4 as model input, regression prediction equations were developed for TC precipitation forecast at 89 stations in Guangxi over 1980–2015 under the same modeling samples, independent samples, and successive prediction method. In the same way, stepwise regression predictors were recalculated in each forecast.

    It should be noted that all parameters in successive predictions are kept unchanged, and when a modeling sample is added, model input is recalculated, so the prediction is objective.

4.5 Performance definitions

For comparison purposes, three measures of rainfall are employed: the root-mean-square error (RMSE), bias score (BIAS), and equitable threat score (ETS). The RMSE is often employed to verify the amount of error in the rainfall forecasting. RMSE is commonly defined as

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(\hat{y}_{i} - y_{i} )^{2} } } $$
(14)

where \( y_{i} \) is the desired output; and\( \hat{y}_{i} \) is the actual output. Generally, the smaller the RMSE criteria, the better is the performance of the predicted outcomes.

BIAS measures the ratio of the predicted rain frequency to the observed frequency, regardless of forecast accuracy; if BIAS is equal to 1.0, then the predicted rainfall frequency is the same as that observed (McBride and Ebert 2000; Ebert et al. 2003; Wei 2012). BIAS can be employed to assess the tendency of the model to under- or overpredict rain occurrence. BIAS is defined as

$$ {\text{BIAS}} = \frac{H + F}{H + M} $$
(15)

where H is the frequency of correct predictions of rain occurrence; F is the frequency of incorrect predictions of rain occurrence; and M is the frequency of rain occurrences that are not predicted.

ETS has been used for several decades to measure the correspondence between the forecasted and observed rain occurrences at most operational centers (Schaefer 1990; Ebert et al. 2003). The “equitable” measure accounts for the random chance that both forecasted and observed rain occurrences. ETS is defined as

$$ {\text{ETS}} = \frac{{H - H_{\text{random}} }}{{H + M + F - H_{\text{random}} }} $$
(16)

where H random = (H + M)(H + F) / (H + M + F + Z) and Z is the frequency of correct forecasts of no rain. The total number of forecasts (or observations) is (H + M + F + Z). There are 8366 records (94 independent samples × 89 stations) in this paper. ETS ranges from − 1/3 to 1, with a value of 1 indicating perfect correspondence between predicted and observed rain occurrences (Ebert et al. 2003; Wei 2012).

4.6 Model evaluation and discussion

In this section, to identify the suitable model, the RMSE, BIAS, and ETS were employed. Figure 6 shows the results using the FNN–LLE, interpolation method by ECMWF, and stepwise regression approach in the years 2011–2015 prediction. As can be seen, FNN–LLE is the most precise of these three models for each year, indicating that FNN–LLE simulations give better performance than those of interpolation method by ECMWF and stepwise regression approach in precipitation prediction.

Fig. 6
figure 6

RMSE measures of precipitation predictions by FNN–LLE model, interpolation method by ECMWF, and stepwise regression method

Full size image

To evaluate the model capability in estimating light, moderate, and heavy rains during the TC period, both BIAS and ETS were computed to give a correct estimate of the observed rainfall over a certain threshold. For BIAS, if BIAS > 1.0, the model overpredicts rain occurrence; otherwise, the model underpredicts rain occurrence. ETS measures the number of forecast fields that match the observed threshold. According to Table 5, the stepwise regression model tends to overestimate peak and cumulative rainfall amounts; the interpolation method by ECMWF tends to underestimate rainfall at thresholds < 30 mm d−1 and inclines to yield overestimations of rainfall at thresholds > 30 mm d−1. In general, FNN–LLE having BIAS and ETS close to 1.0 and gives a better estimation than do interpolation method by ECMWF and stepwise regression, meaning that FNN–LLE achieves better prediction performance.

Table 5 Rain contingency table for the specific threshold and measures of BIAS and ETS
Full size table

5 Summary

Extreme disaster events are frequently caused by heavy rainfall associated with TC landfall. Indeed, the six top heaviest rainfall events on record in China are all associated with TCs. Therefore, it is an important research content and forecasting difficulty of meteorological disaster prevention and mitigation to accurately predict the precipitation of TC rainstorm. This study developed the FNN–LLE for forecasting the daily precipitation amounts during typhoons. Furthermore, the FNN–LLE model was compared with the interpolation method by ECMWF and stepwise regression.

The developed models were applied to rainfall predictions at the 89 stations in Guangxi, China. This study analyzed data related to the large-scale circulation of TC activity and daily precipitation amounts at the study site. A total of 172 typhoon events affecting Guangxi from 1980 to 2015 were selected. The developed FNN–LLE model input is constructed from potential predictors by employing both a stepwise regression method and an LLE algorithm to obtain a small network architecture, and the FNN model is combined by fuzzy systems and neural network to enhance the capacity of a neural network for processing rainfall predictions.

The predictions obtained by the FNN–LLE model, interpolation method by ECMWF, and stepwise regression approaches were compared. Meanwhile, the RMSE, BIAS, and ETS were employed to assess the forecasted results. Results show that the RMSE values of 21.94, 24.07, and 25.22 are obtained by FNN–LLE model, interpolation method by ECMWF, and SRM, respectively. In addition, FNN–LLE model having average BIAS and ETS values close to 1.0 gave a better prediction than did the interpolation method by ECMWF and SRM models.

Noted that the factors used in the paper are all based on the NCEP\NCAR model. In the future, the forecast accuracy will be improved if the T639 model products in China or the European Center fine meshes are directly used as predictors. It is worth to carry out further research.