1 Introduction

Researchers have put significant work into optimizing cycling performance by studying various bicycle designs, equipment modifications, cycling techniques, and pacing strategies. One aspect of cycling that has been relatively unexplored is the track cycling standing start. In certain track cycling events, such as the team sprint, the cyclist starts with the bicycle fixed in a gate and then accelerates to top speed as quickly as possible once the gate is released. During the standing start, the cyclist rises from the seat and attempts to use the additional degrees of freedom to maximum advantage. There is a desire to better understand the optimal kinematics for the standing start.

Previous researchers have utilized experimental studies to analyze the standing start [1,2,3,4]. One of the drawbacks, as with many experimental studies, is the number of experiments required to understand the technique and test different variations. Predictive computer simulation with forward dynamics is useful in this regard because it allows for numerous trials under various controlled conditions in a relatively short period of time.

In predictive simulation, the optimal force or torque activations are found using a representative objective function, such as achieving the maximum distance in a fixed time duration. This can be contrasted with “data tracking” simulation, which is not predictive in nature. Such simulations require collecting experimental data and then driving the model to track this data. Several researchers have used data tracking or similar methods in pedaling applications [5,6,7,8,9]. For certain research questions, predictive simulation is more useful because no experimental data is used to drive the simulation, and therefore, it does not require the detailed data collection needed for data tracking. Additionally, numerous “What if?” simulations can be run to study how the optimal technique is affected by changes to model parameters such as the gear ratio or handlebar position.

There are two main ways to actuate a biomechanical model when using forward dynamics. One is to include individual muscles and to activate them using muscle excitations. This can become computationally intensive for predictive simulation using optimal control methods because of the increased number of state variables. An alternative is to use applied torques to represent the net effect of muscle forces at a joint. This reduces the number of variables and simplifies the optimal control problem. Muscle torque generator models have been implemented previously in predictive simulation of human movement, including various sports applications [10,11,12,13].

A commonly used approach for finding the optimal inputs in predictive simulations of human movement is to employ direct methods of optimal control. In direct methods, the control and/or state variables are approximated with a polynomial function, and the optimal control problem is transcribed to a non-linear programming problem. Optimal control has previously been applied to forward dynamic simulations of pedaling. Kaplan and Heegaard [5] used direct collocation optimal control for a data tracking simulation of ergometer pedaling. Raasch et al. used optimal control with a musculoskeletal model for predictive simulation of maximal seated start-up pedaling (i.e. starting with zero velocity) [14, 15]. Zignoli et al. recently used optimal control via indirect methods with a joint torque-driven model for predictive dynamics of seated submaximal cycling [11]. A common theme among previous dynamic models is that many have focused on seated ergometer pedaling or steady-state cycling and have used some form of resistive torque or effective inertia to provide the resistance at the crank [5,6,7,8,9, 11, 14,15,16,17,18,19,20]. They ignore the upper body because, for seated pedaling, it does not contribute to the pedaling motion. They do not model the bicycle itself because, for steady-state cycling and ergometer pedaling, the resistance at the crank can be modeled more easily in the aforementioned ways. Modeling the bicycle allows one to incorporate the bicycle dynamics when examining the effects of shifting body positions. This becomes important when considering standing starts in track cycling.

Schwab and Meijaard [21] conducted a review on previous bicycle dynamics research, which is largely focused on bicycle stability and control methods for balance and steering. In these models, the rider is often ignored or only given upper body movement for stability and not lower limb movement for propulsion. When the cyclist dynamics have been included, it has often focused on the bicycle suspension such as in mountain bicycles [22, 23]. Researchers often use nonholonomic constraints for the wheel-ground contact and make the assumption there is no tire slip, which may not be valid for the accelerations seen in standing starts. For more detailed wheel-ground contact, researchers employ a tire model, with the Pacejka tire model [24] being the most common for multibody vehicle dynamics. Partially due to the difficulties of obtaining the necessary experimental tire force data, Bulsink et al. [25] is one of the few to use the Pacejka tire model when they utilized the results of Doria et al. [26] to implement the Pacejka tire model in their investigation of bicycle stability.

There is a lack of models that take into account both cyclist and bicycle dynamics simultaneously. This work covers the development of a combined cyclist and bicycle model that can be utilized for predictive simulations of maximal start-up cycling (i.e. a track cycling standing start) using optimal control methods. A useful model of a standing start needs to incorporate bicycle dynamics, including tire models, and cyclist dynamics, including the upper body. To our knowledge, there is no previous modeling and simulation study of track cycling standing starts. The goal is to use experimental results and predictive simulations to gain a better understanding of what the optimal full body kinematics might look like for standing starts.

2 Methods

2.1 Standing start experimental data collection

Six standing starts were performed on the track at the Mattamy National Cycling Centre in Milton, Ontario by a single male member of the Canadian track cycling team who participates in the team sprint event. To measure joint kinematics, electrogoniometers (Biometrics, Ltd.) with adapters for wirelessly transmitting the data (Trigno Wireless EMG, Delsys Inc.) were attached at the joints of interest in the model (both ankles, knees, and hips, single elbow and wrist). Electrogoniometers cannot measure shoulder angles reliably. Right and left upper arm motion was assumed to be similar so additional electrogoniometers were not purchased for both arms. The two ankle goniometers were damaged during the cyclist’s warm-up, so the ankle measurements were not successful. The ankle angle measurements displayed here for comparisons with the predictive simulations are from previous testing that was conducted to assess the efficacy of electrogoniometers for track cycling standing starts. These test conditions were not identical, but the other joint angle ranges appear to be similar so it can give an idea of what these ankle joint angles look like in experiments. The electrogoniometers give a relative angle between the endblocks so calibration measurements were obtained by recording the offset when the joints were placed at zero-degree joint angles. Electrogoniometers are not ideal sensors for measuring joint kinematics; however, there are limited tools available for measuring joint kinematics in the field over a 30 meter distance.

Crank data was collected at 80 Hz using instrumented cranks from 4iiii Innovations, Inc. The crank sensors operated independently of each other so independent right and left side crank torques were collected, which were then summed to get the total crank torque. Inertial Measurement Units, or IMUs, (Mbientlab, Inc.) collecting at 100 Hz were placed on the crank and on the frame. The IMU collected angular velocity of the crank to get a high-frequency cadence measurement, which was integrated to get the crank angle. The accumulation of integration error over time for the crank angle calculation was corrected using a magnetic reed switch in the 4iiii’s system triggered once per pedal stroke. The automatic track timing system was used to record time stamps at the gate release and at the next track landmark 15 meters from the gate. This landmark was the primary point for comparing the distance traveled between the experiment and the simulation. Additionally, bicycle position and velocity curves were approximated using the accelerometer data from the IMU on the frame. These curves are useful to observe their trends, even if their exact values have some degree of uncertainty related to the accumulation of integration error. The track timing system was used to evaluate the position approximation from the IMU and provide an understanding of its accuracy.

Post-testing, the data streams were synchronized by aligning accelerometer data from each of the streams. An electromyography (EMG) sensor from the Delsys system was placed on the frame to allow for the synchronization of electrogoniometer data through the accelerometer in the EMG sensor. This meant that the IMU, crank arms, and electrogoniometers all had accelerometer data in their data streams. Prior to the cyclist getting on the bike, the bicycle was jerked laterally to create an acceleration spike in the data streams. The data streams were synchronized by aligning the time of the acceleration peak in each stream.

The cyclist’s feet were clipped into the pedals, as is typical in track cycling. The bicycle started fixed in the gate, which uses a pneumatic mechanism that clamps the bike on the seat post, just below the seat. The bicycle was then released automatically as the clock hit zero. The cyclist was instructed to use his normal technique and give high effort up until the first turn (approximately the first 30 meters).

2.2 Model development

The model was developed using the MapleSim software (Maplesoft Inc.) because its multi-domain capabilities allowed the bicycle and cyclist to be modeled in the same software. Additionally, its symbolic processing and optimized code generation capabilities make it an excellent choice for developing and exporting computationally-efficient forward dynamics models.

2.2.1 Bicycle model

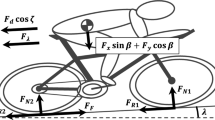
The bicycle model consisted of four bodies: the rear wheel, the front wheel, the frame/fork/handlebars, and the crank. Revolute joints connected the rear wheel to the frame and the front wheel to the fork. The crank was modeled as a single link connected to the frame by a revolute joint. The rear wheel motion was connected to the crank motion using an ideal gear with a 50:14 (3.57:1) gear ratio, which was the same as the fixed gear ratio used by the cyclist in the experiments. During a standing start, the cyclist is in the straightaway of the track and is traveling in a relatively straight path. To simplify the model for straight-line cycling, a planar bicycle model was implemented. A revolute joint was not included between the frame and the front fork/handlebars, and the bicycle was constrained to remain upright and follow a straight path. These simplifications eliminated the need for a steering or balancing controller. Adding a steering or balancing controller was not the main focus of the study and would have increased computation time. With these simplifications, the bicycle model had five degrees of freedom: crank rotation, front wheel rotation, longitudinal and vertical translation, and pitch (frame rotation).

The setup of the bicycle model, including overall bicycle dimensions as well as handlebar position and crank length, was set to match that of the Look L96 track cycling bicycle used by the cyclist in the experiments. Moment of inertia and center of mass locations were determined from a SolidWorks model of a bicycle frame that was developed using the bicycle dimensions. Aerodynamic drag was ignored, as it is not likely to be a major factor when traveling at low speeds during start-up cycling.

2.2.2 Tire model

MapleSim contains built-in components for the Pacejka tire model [24] that were used for formulating the tire force and moment equations. The Pacejka model requires parameters that are determined from experimental data, but Pacejka parameters have not been reported for track cycling tires. Instead, parameters for road tires reported by Bulsink et al. [25] were used, with the exception of the rolling resistance coefficient, which has been reported for track cycling tires to be approximately 0.0023-0.0024 [27, 28]. There are likely noticeable differences in the longitudinal slip parameters between road cycling tires and track cycling tires, but it is unknown whether they would have a noticeable effect on the results of the simulation.

For simplicity, the surface for the straights was modeled as being flat in this study rather than the 13-degree banked straights for an Olympic-category velodrome. We assumed the camber forces and moments from the banked track have minimal effect when the model was constrained to remain upright. Zero-velocity maneuvers (e.g. starting from rest) result in infinite slip, so relaxation lengths must be used when calculating slip in the Pacejka tire model. When using relaxation lengths, the slip is treated as a state, with its derivative a first-order differential equation containing the relaxation lengths. For simplicity, constant relaxation lengths of 0.3 m were used in this study [29].

2.2.3 Cyclist model

The cyclist model consisted of ten rigid bodies: two feet, two shanks, two thighs, upper arm, forearm, hand, and the head + trunk (see Fig. 1). The upper limb motion was assumed to be symmetric so the right and left arms were lumped together. Revolute joints were used to represent each of the joints (shoulder, elbow, wrist, hips, knees, and ankles). The spine curvature was given a fixed angle of 25 degrees between the abdomen and the thorax in the trunk segment. The cyclist’s hands were rigidly fixed to the handle bars at a 45-degree angle. The cyclist’s feet were clipped into the pedals using toe clips, thus allowing the foot/pedal to be constrained to the crank with a revolute joint. Limb segment properties were set using anthropometric data from de Leva [30], which were scaled to match the subject from the standing start experiment. The cyclist and bicycle together form a closed kinematic chain due to the two feet being fixed to a single crank and the hand being fixed to the handlebars. Therefore, there are more coordinates (14) than there are degrees of freedom (10), resulting in a system of 18 differential-algebraic equations (DAEs) for the dynamic equations.

Fig. 1
figure 1

The combined cyclist and bicycle model in MapleSim

Full size image

The cyclist model was driven using nine muscle torque generators (one at each of the cyclist’s joints), which represent the combination of muscle forces acting on a joint. Anderson et al. [31] developed a joint torque model for the lower limb that was implemented here. The active joint torque is scaled based on the joint angle and angular velocity, representing the muscle force–length and force–velocity relationship. The scaling function is piecewise to account for both concentric and eccentric muscle contractions. The parameters from Anderson et al. were for “average” 18-25 year old males. Olympic cyclists are far from average so it is not clear how well these scaling parameters represent the force–velocity and force–length relationships of their muscles. Maximum torque values were determined from the results of Kordi et al. [32], who measured maximum isometric joint torques for competitive cyclists. Each joint had its own maximum torque rate of change that was based on rate of muscle activation [33]. In addition to the active joint torques, passive joint torques were also included. Passive torques represent the passive forces that are generated by the stretching of muscle tissue, tendons, and ligaments. Riener and Edrich’s [34] model for lower limb passive joint stiffness was chosen based on its ability to take into account adjacent joint angles.

A simpler active joint torque scaling model that only scales based on joint angular velocity was used for the upper limb joint torques. This torque scaling method has been implemented in previous upper limb joint torque applications [12] and was based on the work done by vanSoest et al. [35]. Maximum upper limb joint torque values were taken from Garner and Pandy’s study of the upper limb [36].

To assess the accuracy of the cyclist model, ergometer pedaling simulations were compared against ergometer pedaling experimental results for members of the Canadian track cycling team. The results are contained in a previous paper on the preliminary development of the cyclist model and in the thesis covering this project [37, 38]. Overall, the simulation results were similar in nature to the experimental results, indicating the cyclist model was an appropriate representation of an Olympic track cyclist.

2.3 Optimal control using direct collocation

The General Purpose Optimal Control Software, Version II (GPOPS-II) optimal control package from Rao et al. [39] was used together with an interior-point optimizer (IPOPT) to solve the optimal control problem for the joint torque activations that achieve the maximum distance in a fixed amount of time. GPOPS-II uses orthogonal collocation, which is a direct optimization method.

The dynamic equations for the model, which were a system of DAEs, were exported from MapleSim. In GPOPS-II, the dynamic equations can be left as DAEs, with the algebraic constraint equations being handled as path constraints. The differential equations with the reaction forces are included as the dynamic constraints. The reaction forces were treated as states, while the derivatives of the reaction forces, whose equations are not automatically derived and included in the dynamic equations exported from MapleSim, were treated as controls in the GPOPS-II software. Treating them as controls (i.e. inputs to the simulation) allowed GPOPS-II to freely determine the values for the derivatives of the reaction forces that satisfy the dynamic equations and constraint equations at each time point, without needing to derive the equations for the derivatives of the reaction forces.

Setting up the problem required specifying bounds for the 43 states (generalized coordinates and their derivatives, tire slip, active joint torques, and reaction forces) and 13 controls (joint torque rates of change and the reaction force derivatives). The bounds for the joint angles and joint angular velocities were set at values that would not restrict the natural motion of the cyclist. However, path constraints were placed on the position of the hip joint center that prevented it from going through the seat or seat post. It is also required to specify an initial and final guess for the control and state variables, along with any intermediate guesses. The initial and final guesses were set based on the experimental results, to give a reasonable starting point for the optimization. No intermediate guesses were used to avoid driving the simulation to a particular result. The initial and final guesses only seem to influence the CPU time and do not seem to influence the optimal solution. There was a tuning process required in generating these simulations in order to find the bounds, mesh numbers, tolerances, and other parameters in the GPOPS-II setup. This was a time-consuming process based on the simulation lengths so it is likely that similar results could be attained with shorter run time with further tuning of the setup parameters.

The problem was formulated as a two-phase problem, separated into the pre-launch and launch phases. To model the pre-launch phase where the seat post is clamped in the gate, the bicycle is treated as being completely fixed, leaving the model with only the cyclist degrees of freedom. The time duration of the simulation was 5 seconds in total, with the pre-launch designated to last 1 second and then continuing into 4 seconds of the launch phase. Since our primary focus was on the initial straightaway, we chose a time frame long enough for it to ensure optimal performance over the distance of interest but kept it short enough to have more manageable computation times. Four seconds is sufficient to achieve a state with high enough velocity and cadence where the drive–reset motion is reduced and more resembles steady-state pedaling.

The objective for the simulations was to achieve the maximum distance in the given time period. This represents the objective on the track, where the cyclist wants to cover the maximum distance possible in the initial portion of the event, to get up to top speed as quickly as possible. Therefore, the following cost function was minimized, where \(x_{f}\) is the final distance traveled:

$$ J = \frac{1}{x_{f}} $$
(1)

Other components that have been used in optimization of steady-state pedaling, such as minimization of joint torques or minimization of jerks, were also considered. They were ultimately not used, because the efficiency and smoothness of the motion are not a significant concern to the cyclist in comparison to maximizing the distance traveled for the first few seconds of the standing start. An additional component of the objective function was considered for the pre-launch phase to help drive the solver to the optimal solution for the pre-launch. In the end, this was not needed because the solver was able to discover that launching forward at the end of the pre-launch helped achieve maximal distance.

3 Results

3.1 Experimental results

Figures 2 and 3 contain a selection of the experimental results from the standing start trials 2–6. In trial 1, the cyclist momentarily lost balance during the trial, causing the bicycle to swerve and slow down. This was not representative of an effective standing start so trial 1 was ignored for data analysis. In these figures, the dashed lines correspond to the left leg and the solid lines correspond to the right leg.

Fig. 2
figure 2

Right and left hip joint angles from the experiments. 0 degrees is for the joint in the neutral position (extension)

Full size image
Fig. 3
figure 3

Right and left crank torque from the experiments

Full size image

After many hours of practice, the cyclist has developed the “muscle-memory” to be able to consistently repeat the technique, which was noted in all the experimental results. Although the cyclist is consistent, there are noticeable asymmetries between the right and left side. In Fig. 2, one can see asymmetries in the hip joint angles. There are secondary peaks in the hip angles corresponding to the cyclist thrusting the hips back in the “reset” motion (see Sect. 3.2 and Fig. 4 for a description of this motion). These peaks were more pronounced in the right side than the left side. In Fig. 3, we can see that the right side is producing more torque than the left side. The decrease in torque over time is expected as the angular velocity increases; however, even in the directly subsequent pedal strokes, the peaks for the right side are larger than the left.

Fig. 4
figure 4

Comparison of the poses in four key stages of the standing start technique. (a) Pre-launch, (b) gate release, (c) drive, (d) reset

Full size image

3.2 Simulation results

Figures 4–8 contain the results of the simulation, with comparisons to the experimental results where applicable. The computation time was 279 minutes on an Intel® Core™ i7-6700 CPU at 3.40 GHz with 16 GB RAM for the track standing start simulation.

Figure 4 contains still frames of the cyclist poses in key stages of the standing start experiments and simulation. Both rock their hips back in the pre-launch (Fig. 4a) in a similar nature, with the cyclist in the experiment extending back slightly farther. One of the most noticeable differences between simulation and experiment is that the simulation tends to be farther forward, with a more elevated hip position at gate release than in the experiments (Fig. 4b). This difference is likely due to the fact that the simulation can time the gate release perfectly. In experiments, the cyclist tended to err on the side of caution to make sure the gate is fully released at the end of their pre-launch.

As they launch out of the gate, they drive their hips forward relative to the bicycle. The “drive” position (Fig. 4c) is fairly similar between the two, but this is where the planar nature of the model results in some differences. The actual cyclist tends to have a more out-of-plane elbow flexion, coming from shoulder rotation. While the trunk is in a similar position and orientation for both, the arm kinematics to achieve it are different. Furthermore, we can see the spine curvature changing in the experiments, which cannot be captured by this model.

As the crank approaches a vertical position (referred to as top dead center), the cyclists enter a mechanically inefficient position. To overcome this mechanically inefficient position, the cyclists shift their hips backwards relative to the frame, in the process thrusting the bicycle forward underneath them and propelling the crank through the top dead center position. For the “reset” position (Fig. 4d), the general pose is similar between the simulation and experiment and occurs at a similar 45-degree crank angle. After passing through top dead center, the cyclist drives forward again, repeating this periodic motion several times; the amplitude less pronounced with each pedal stroke.

The general notation for all plots in Figs. 5–9 will be to use solid curves for simulations and dashed curves for experimental results. The vertical dashed line represents the gate release, separating the end of the pre-launch phase and beginning of the launch phase. A crank angle of 0 degrees corresponds to the right pedal in the top dead center position.

Fig. 5
figure 5

Bicycle kinematics

Full size image

Tables 1 and 2 give comparisons at the point in the experiment when the cyclist crossed the track landmark 15 meters from the gate (\(t\approx 3\) seconds). In these tables, distance and time for the experiment were determined from the track timing system, while the velocity, pedal strokes and cadence were determined from the IMUs as described in Sect. 2.1. The simulation outperforms the experiments, and this is primarily due to the ability of the simulation to almost perfectly time the gate release and transfer all of its initial momentum generated in the pre-launch phase to the bicycle. Figure 5 contains the bicycle kinematics, including the position and velocity of the frame. The position estimation from the IMU was 14.74 m at 3.01 seconds, giving it an error of 0.26 m (1.7% relative error) when compared to the track timing system. Therefore, the experimental results for the bicycle kinematics in Fig. 5 are slight underestimations, but the error is relatively small. The peaks and valleys in the bicycle velocity, which were also present in the crank angular velocity, correspond to the cyclist drive and reset maneuvers. The initial crank angle chosen by the simulation was 81 degrees compared to approximately 75 degrees for the cyclist in the experiments.

Table 1 Comparison of results at \(t = 3\) seconds
Full size table
Table 2 Comparison of results at \(x = 15\) meters
Full size table

Figure 6 contains the crank torque and power. The simulations generate greater crank torque than in the experiments at the beginning, peaking at approximately 550 N⋅m in the simulation compared to 450 N⋅m in the experiment. Power is greater in the simulation because it generates similar amounts of crank torque while at a higher cadence.

Fig. 6
figure 6

Crank torque (a) and power (b) for the standing start

Full size image

Figure 7 contains the right and left leg joint angles plotted versus the total crank angle. Making comparisons between experimental and simulated hip angles can be difficult due to the differences between the fixed spine curvature angle in the model and the varying spine curvature in the experiments. In the simulations, the intermediate peak in the hip angles corresponding to the cyclist reset motion only occurs twice, as opposed to the several times that are seen in the experiments. The main use of the ankle joint angle is for comparison of general trends of the joint kinematics, since it came from a different experiment. There was more ankle dorsiflexion in the simulations. Overall, the simulations appear to have more left–right symmetry than the experimental results.

Fig. 7
figure 7

Lower limb joint angles versus total crank angle for standing starts. For hip (a) and knee (b), 0 degrees is the neutral position (full extension). For the ankle (c), 0 degrees is perpendicular to the shank and positive angles correspond to dorsiflexion

Full size image

There were significant differences between the upper limb joint angles in the simulations and in the experiments. The physiological nature of the shoulder, elbow, and wrist joints allows for significant movement out of plane so the planar modeling is not a good representation for the upper body. These joint angles may be significantly different between the simulation and experiment, but that may not affect the hip joint center position, which matters more than the individual upper limb joint angles when it comes to generating crank torque. The same hip position could be obtained with different combinations of upper limb joint angles depending on how far out of the plane they go.

Figure 8 shows the hip joint center kinematics. The simulation starts by rocking the hips back and stretching the upper body so that the hips are above the seat and almost as far back as possible. The simulation then launches the body forward to its forward-most position. It begins the reset motion at about 45 degrees prior to reaching top dead center (crank angle of 315 degrees). Looking at Fig. 8b, the simulation tends to reach its peak reset position at approximately 45 degrees past top dead center (TDC) with each leg, at which point it is prepared for driving the hips forward again. The experimental reset position also occurs when the crank angle is approximately 45 degrees. The higher crank angular velocity in the simulation means we do not see the same amount of hip movement as in the experiments. At higher crank angular velocities, the drive–reset technique becomes less effective, as it is more difficult to go through the motion at that speed.

Fig. 8
figure 8

Hip joint center kinematics. (a) Hip position in the sagittal plane including both the pre-launch and the launch phase. (b) Hip position versus the crank angle relative to top dead center for the first two pedal strokes after gate release

Full size image

Figure 9 contains the joint torques and torque activations for each lower limb joint. The torques are close to maximally activated for most excitations of the hip and knee joints. The hip joint torque has a different profile in the first pedal stroke. Both legs have periods of eccentric contractions. This is likely related to driving the hip position backwards in the reset motion.

Fig. 9
figure 9

Lower limb joint torques and activations. R and L denote right and left side. Ts refers to the scaled torque, Tpre refers to the pre-scaled torque activation, and Tiso refers to the isometric torques for flexion and extension (i.e. torque bounds)

Full size image

4 Discussion

The simulation gives an idea of the optimal standing start technique. Based on the results of these experiments and simulations, it seems that the standing start technique being currently used is close to what was found by the optimal simulation. Both seem to be performing the drive and reset motion at similar points in the pedal stroke. The simulations and experiments are close enough in nature that any differences seen cannot be clearly distinguished as improvements that should be made without questioning the effects of the assumptions and simplifications that have been made in the model.

After seeing some variability among the solutions obtained during the process of tuning the optimal control parameters, the conclusion was reached that these results may not have completely converged to an optimal solution. There was not a sensitivity study or convergence study to analyze how close these results are to the global optimum. While it may not be a global optimal result, the simulation still presents a highly-effective method of completing a standing start. These uncertainties with the results are largely due to the lengthy computation time and the difficulties posed by tuning the GPOPS-II setup. For a large problem such as this, GPOPS-II seems to be fairly sensitive to the bounds and parameters.

It is interesting to see the ability of the solver to find key characteristics of a standing start solely based on the goal of achieving maximal distance. Entering the project, it was anticipated that more complex objective functions might be needed, but fairly representative simulations can be achieved with a simple objective function. It should be noted that the optimal trajectories towards the end of the simulated trial are less reliable and less meaningful than those during the main portion of the trial. Based on the objective function, at the end of a trial, the model may attempt to maneuver itself in a way that will increase the final distance slightly at the expense of future performance (e.g. driving the bicycle frame forwards in the last second of the simulation).

The aspect of the simulations that is most unrealistic is the initial launch out of the gate. The transfer of momentum is optimized because the simulation is able to precisely constrain the upper body motion relative to the frame and do so at the optimal time as it launches out of the gate. This is unrealistic due to the complicated nature and difficult timing of such a maneuver. One difficulty with predictive simulations is that the model can be manipulated in very precise ways to maximize performance that might not be feasible in real life due to the precision that would be required for such a movement. In general, caution must be taken in utilizing the results because the simulation can be quite precise with its movements.

Due to the large number of parameters and long computation time, it was not feasible to conduct a sensitivity analysis to further evaluate the model and simulation. For future work, a limited sensitivity analysis could be conducted on key parameters. One of the main points of interest would be examining how the initial crank angle affects the simulation results, and also examining which parameters have the strongest effect on the optimal initial crank angle. This could determine whether a cyclist should change from their preferred crank angle, or whether there is a range that can be used to achieve similar performance. The impact of other factors relating to the bicycle such as gear ratio, crank length, and handlebar position should also be explored for similar reasons. The cyclist parameters such as anthropometric properties should be analyzed to see how much the optimal technique changes for different cyclists. The effect of muscle torque generator models and their properties such as maximum torque, torque-velocity scaling, torque-angle scaling, and passive torques should also be explored. Knowing the effect of these properties could direct cyclists on how they should focus their training. It would also provide direction for researchers on what parts of the muscle torque generators need to be modeled most accurately, and if other torque scaling models may be more accurate representations of an elite-level cyclist. Computation time is the main limiting factor on the completion of these numerous “What if?” simulations that are of interest.

There are some limitations to the results presented in this study. One is the use of muscle torque generators rather than a full musculoskeletal model for the lower limbs, in the process ignoring individual muscle properties and simplifying the activation dynamics, force–length scaling, and force–velocity scaling. The additional state variables required make a full musculoskeletal model impractical for use in an optimal control problem of this scale. The primary simplification in the development of the bicycle model was the constraint to remain upright and follow a straight line. A controller for steering and balancing would be difficult due to the oscillating leg masses and the trunk oscillating front to back. The tire models would also become more complicated as they would require lateral dynamics and camber forces to be included. While it was not entirely accurate, the bicycle model as a whole was a reasonable approximation of a generic track bicycle. The primary limitation of developing a more complex and accurate model is the computation time required.

5 Conclusions

A two-legged cyclist and bicycle model was developed for predictive simulations of start-up cycling using optimal control methods. The model replicated key features of the standing start technique, including the pre-launch, drive, and reset motions. A shortcoming of the predictive simulation is long CPU times, which is expected for the optimal control solution of complex multibody dynamics. The overall modeling and simulation approach, and more specifically using direct collocation for predictive simulation of human movements, is effective in generating a standing start technique that resembles that used in real life. The comparison of the simulations and experiments did not indicate a need for any major changes to the standing start technique. For a sport that has been around for many years, it was expected that the technique is fairly well optimized, but details might be refined and better understood.

The model can subsequently be used to examine the effects of changing various aspects of the bicycle setup (e.g. handlebar position, crank length, gear ratio, etc.) as part of the optimization. There is the potential to observe the effects of varying joint strengths and how that affects the optimal technique. The key with these applications is knowing that the solver has converged and that the differences in the optimal solutions are due to the change in parameter and not just that the solver is converging to a different local optimum.