Dynamics of a vibro-impact self-propelled capsule encountering a circular fold in the small intestine

Abstract

Given the anatomy of the small intestine, this paper investigates the dynamics of a vibro-impact capsule moving on an intestinal substrate with the consideration of a circular fold which provides the main resistance for the capsule’s progression. To this end, a new mathematical model of the capsule-fold contact that can depict the entire procedure of fold crossing is proposed. Our bifurcation analyses suggest that the capsule always performs period-1 motion when the driving force is small, and fold crossing requires a large excitation amplitude, especially when the duty cycle ratio is small. By contrast, the excitation period of the capsule does not have a strong influence on fold crossing. It is found that the inner mass, capsule mass, frictional coefficient and fold’s height have a significant influence on capsule’s crossing motion. We also realise that Young’s modulus of the tissue has a critical influence on the bifurcation pattern of the capsule, where a stiffer tissue may lead to the co-existence of three stable attractors. On the contrary, the capsule’s length and stiffness of the impact springs have less influence on the capsule’s dynamics. The findings of this study can help with the optimisation and control of capsule’s locomotion in the small intestine.

1 Introduction

Before the introduction of capsule endoscopy [1], visualisation of the stomach, the small bowel and the colon was realised by using the fibre-optic endoscopy, which has many limitations in practice, such as patient’s discomfort, long duration of diagnosis and limited reachable area. As an alternative technology, capsule endoscopy becomes the primary modality for small-bowel diagnosis, especially for the patients with the Crohn’s disease, the refractory celiac disease, and the Peutz Jeghers syndrome, which require repeated monitoring of the ongoing active disease [2]. Many commercial capsules are passively driven by the peristaltic wave of the gastrointestinal tract, lacking control of their locomotion speed, so fast translating capsule could miss some diseases during the procedure. For example, in the detection of obscure gastrointestinal bleeding, the reported accuracy is around 60% [3]. Thus, various active capsules have been being developed for effective targeting movement and precise diagnosis [4].

The simplest active capsule uses screw impeller [5], which propels the capsule by fluid dynamic pressure. Gao et al. [6] designed a tetherless inchworm-like capsule robot to explore the intestine, which used an expanding mechanism to contact the digestive tract for locomotion. In a more complicated prototype, several legs were used for both locomotion and anchoring [7]. These capsules adopt various external mechanism, where the moving parts are potentially hazard to the gastrointestinal tract. In clinical practice, an average size of 26 mm in length and 11 mm in diameter without any sharp edges is suggested for the design of a safe capsule accessible to the whole digestive system [8]. Therefore, a feasible option is to encapsulate all the necessary components by using a shell and without employing any external mechanisms. Such a design is hard to propel but can benefit miniaturisation. To drive this kind of capsule robot, Erin et al. [9] employed the power for magnetic resonance imaging to generate strong magnetic fields for controlling its position and orientation. Instead of a constant driving force, periodic vibro-impact actuation can also be used for high-efficient propulsion [10].

Design of an active capsule endoscope should consider the anatomy of the digestive system, especially for the small intestine which is beyond the reach of fibre-optic endoscopy. On average, adults’ small intestine has a length of 6 m and a diameter of 3.5 cm, consisting of 0.25 m duodenum, 2.5 m jejunum, and 3.25 m ileum at its proximal, middle, and distal sections [11]. To increase the surface area for slowing down the passage of food and absorbing nutrient, mucosa in these sections is highly folded, with plicae circulares extending transversely for about 50–60% of circumference of the small intestine [12]. A simplified anatomy of the small intestine and a piece of cut-open synthetic small intestine with a circular fold are presented in Fig. 1. For any device entering the small intestine, it is supposed to overcome the resistance of the circular folds for forward locomotion. In our previous studies on the vibro-impact capsule [10, 13, 14], however, only the flat small intestine without the circular folds was considered. The model assumes that the capsule distends the digestive tract in radial direction, and the hoop stress is regarded as the major source of resistance [15].

Fig. 1

(Colour online) a A simplified anatomy of the small intestine and b a piece of cut-open synthetic small intestine with a circular fold

In our experimental study [16], a sharp increase in the resistance was observed when the capsule climbed over a circular fold, showing the significance of considering intestinal anatomy in the design of the vibro-impact capsule system [17]. A pioneering analytical study on the capsule-fold interactive force was performed by Sliker et al. [18], who assumed that the maximum resistance arises when the capsule’s head touches the peak of the fold. However, this presumption is not necessarily true in many cases. Moreover, the model given by Sliker et al. [18] is only applicable for evaluating static resistance, which cannot be used to study the dynamical response of the capsule when it crosses over the fold. Therefore, the model of the capsule-fold interaction should be generalised for analysing the vibro-impact capsule moving in the small intestine.

To this end, this paper is organised as follows. A new mathematical model of the vibro-impact capsule engaged with the small intestine is proposed in Sect. 2, where the circular fold is considered as a major source of the intestinal resistance. Next, bifurcation analysis is performed in Sect. 3, revealing the complex dynamics of the capsule when it engages with the circular fold, and finding the critical driving force required for climbing over the fold. Finally, conclusions are drawn in Sect. 4.

2 Mathematical modelling of the capsule-fold dynamics

2.1 Capsule-fold interaction

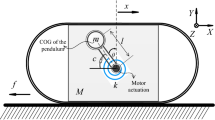
Figure 2 illustrates a small capsule horizontally moving in the x-direction on the small intestine with a thickness of H. The capsule has a cylindrical body with a length of L and a radius of R, which connects its hemispheric head and tail. It is seen in Fig. 2c that the capsule is very rigid compared with the soft tissue, so it is assumed that the deformation of the incompressible and isotropic intestine conforms to the capsule profile. To further simplify the model of capsule-fold interaction, it is assumed that the capsule can only translate in the xoy plane without any rotation [18]. Thus the capsule does not tilt when it contacts the fold as illustrated in Fig. 2d.

Fig. 2

(Colour online) a 3D schematic of the capsule moving on a tissue substrate of intestine with a circular fold, with the b front view and c side view of the capsule-intestine interaction. d The capsule can only translate without any rotation

As seen in Fig. 2b for the front view of cross-section A-A, the capsule’s gravity results in a penetration into the tissue substrate for a depth of $\delta _\text {max}$ in the y-direction. In front of the capsule at $x = x_b$, the small intestine has a circular fold with a height of h and a width of w, which can be described by the following shape function

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} h \cos \left( \frac{x-x_\text {b}}{2 w}\pi \right) , &{} |x-x_\text {b}|\le w,\\ 0, &{} |x-x_b|> w. \end{array}\right. } \end{aligned}$$

(1)

A side view of cross-section B-B for $x\in [x_\text {c}-L-R, x_\text {c}+R]$ is displayed in Fig. 2c, showing a round cross-section of the capsule with a radius of

$$\begin{aligned} \rho (x) = {\left\{ \begin{array}{ll} \sqrt{R^2 - (x-x_\text {c})^2}, &{} x_\text {c}< x \le x_\text {c}+R,\\ R, &{} x_\text {c}-L \le x \le x_\text {c},\\ \sqrt{R^2 - (x-x_\text {c}+L)^2}, &{} x_\text {c}-R-L \le x < x_\text {c}-L, \end{array}\right. } \end{aligned}$$

(2)

where the horizontal position of capsule's head is denoted as x_c. Given Eq. (2) and the capsule’s radius and penetration, one obtains the shape function of the capsule bottom displayed in Fig. 2b as follows

$$\begin{aligned} \begin{aligned} p(x)&= R-\delta _\text {max} - \rho (x) \\&= {\left\{ \begin{array}{ll} R-\delta _\text {max} - \sqrt{R^2 - (x-x_\text {c})^2}, &{} x_\text {c}< x \le x_\text {c}+R,\\ -\delta _\text {max}, &{} x_\text {c}-L \le x \le x_\text {c},\\ R-\delta _\text {max} - \sqrt{R^2 - (x-x_\text {c}+L)^2}, &{} x_\text {c}-R-L \le x < x_\text {c}-L. \end{array}\right. } \end{aligned} \end{aligned}$$

(3)

At a given position, Fig. 2c shows the vertical distance from the capsule’s central axis to the tissue surface as follows

$$\begin{aligned} d(x) = R - \delta _\text {max} - f(x). \end{aligned}$$

(4)

When the distance is larger than the radius of the section, $d(x)>\rho (x)$, there is no capsule-intestine interaction. On the contrary, they have a limited contact angle, $\theta \in [-\alpha (x), \alpha (x)]$ for $d(x)\le \rho (x)$, where $\alpha (x)$ is the limit given by

$$\begin{aligned} \alpha (x,\delta _\text {max}) = {\arccos }\left( \min \left( 1,\frac{d(x)}{\rho (x)}\right) \right) . \end{aligned}$$

(5)

Given the contact angle, the shape function of the capsule bottom is revised to be

$$\begin{aligned} p(x,\theta ) = R-\delta _\text {max} - \rho (x)\cos (\theta ), \end{aligned}$$

(6)

which is compatible with Eq. (3) as $p(x,0) = p(x)$.

Wherever the tissue conforms to the capsule profile, the small intestine deforms from its own shape function to the capsule’s shape function, yielding the deformation

$$\begin{aligned} \delta (x,\theta ) = \max \left( 0, f(x) - p(x,\theta )\right) . \end{aligned}$$

(7)

Dividing the deformation by the original thickness of the substrate yields the tissue strain

$$\begin{aligned} \epsilon (x,\theta ) = \frac{\delta (x,\theta )}{H + f(x)}. \end{aligned}$$

(8)

The strain is then multiplied by the Young’s module of the tissue, E, for the stress

$$\begin{aligned} \sigma (x,\theta ) = \epsilon (x,\theta ) E(x). \end{aligned}$$

(9)

It is seen in Fig. 3a that the stress exerts normal pressure on the capsule shell, which is mapped onto $x-$ and $y-$axes as follows

$$\begin{aligned} \begin{aligned} \sigma _x(x,\theta )&= \sigma (x,\theta )\sin (\varphi ),\\ \sigma _y(x,\theta )&= \sigma (x,\theta )\cos (\varphi )\cos (\theta ), \end{aligned} \end{aligned}$$

(10)

where

$$\begin{aligned} \varphi (x) = {\left\{ \begin{array}{ll} - {\arcsin }\left( \frac{x - x_\text {c}}{R} \right) , &{} x_\text {c}< x \le x_\text {c}+R,\\ 0, &{} x_\text {c}-L \le x \le x_\text {c},\\ - {\arcsin }\left( \frac{x - x_\text {c} + L}{R} \right) , &{} x_\text {c}-R-L \le x < x_\text {c}-L, \end{array}\right. } \end{aligned}$$

(11)

is the angle of anticlockwise rotation from R to $\rho (x)$.

Fig. 3

(Colour online) a Pressure exerted on the capsule shell. b The vibro-impact capsule has an inner mass, which interacts with the shell via a primary damped spring and two impact springs. c Free-body diagrams of the capsule shell and the inner mass

Integrating $\sigma _y(x,\theta )$ over the capsule shell yields the vertical reaction force exerted by the tissue on the capsule as follows

$$\begin{aligned} F_y (x_\text {c},\delta _\text {max}) = \int _{x_\text {c} - L - R}^{x_\text {c} + R}\int _{-\alpha (x,\delta _\text {max})}^{\alpha (x,\delta _\text {max})} \sigma _y(x,\theta ) \rho (x) \text {d}\theta \frac{\text {d}x}{\cos (\varphi (x))}. \end{aligned}$$

(12)

From the free body diagram of the capsule shell in Fig. 3c, one can see that the vertical force cancels the capsule’s gravity by

$$\begin{aligned} F_y(x_\text {c},\delta _\text {max}) = G, \end{aligned}$$

(13)

which implicitly determines the penetration depth, $\delta _\text {max}$, for a given position, $x_\text {c}$. Namely, $\delta _\text {max}(x_\text {c})$ is an implicit function of $x_\text {c}$. Next, integrating $\sigma _x(x,\theta )$ yields the horizontal reaction force as follows

$$\begin{aligned} F_x (x_\text {c}) = \int _{x_\text {c} - L - R}^{x_\text {c} + R}\int _{-\alpha (x,\delta _\text {max}(x_\text {c}))}^{\alpha (x,\delta _\text {max}(x_\text {c}))} \sigma _x (x,\theta ) \rho (x) \text {d}\theta \frac{\text {d}x}{\cos (\varphi (x))}, \end{aligned}$$

(14)

2.2 Model of the vibro-impact capsule

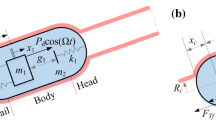
As displayed in Fig. 3b, the capsule’s shell has a mass $m_\text {c}$, inside of which there is a magnet of mass $m_\text {m}$. Compared with Fig. 3c, one can see that the capsule’s gravity involves both of the inner mass and the shell, i.e., $G = \left( m_1 + m_2\right) g$, where $g = 9.81$ $\text {m/s}^{2}$ is the gravitational acceleration. The magnetic inner mass is connected to the capsule shell via a primary damped spring, which has stiffness k and damping c. Besides, there are secondary and tertiary springs in front of and behind the magnet to constrain its motion. They have stiffness, $k_1$ and $k_2$, and gaps, $g_1$ and $g_2$.

The magnetic inner mass is periodically driven by an external excitation as follows

$$\begin{aligned} F_\text {e} = {\left\{ \begin{array}{ll} P_\text {d}, &{} \mod (t,T)\in [0, DT],\\ 0, &{} \ \ \text {otherwise}, \end{array}\right. } \end{aligned}$$

(15)

where $\mod (t,T)$ indicates t modulo T, and $P_\text {d}$, T and $D\in (0\%,100\%)$ are the amplitude, period, and duty cycle ratio of the force, respectively. Via the springs, the inner mass drives the capsule shell by the following piecewise linear interactive force

$$\begin{aligned} F_\text {i} = {\left\{ \begin{array}{ll} k x_\text {r} + c v_\text {r} + k_1 \left( x_\text {r} - g_1\right) , &{} \text {if } x_\text {r} > g_1,\\ k x_\text {r} + c v_\text {r}, &{} \text {if } -g_2 \le x_\text {r} \le g_1,\\ k x_\text {r} + c v_\text {r} + k_2 \left( x_\text {r} + g_2\right) , &{} \text {if } x_\text {r} < -g_2, \end{array}\right. } \end{aligned}$$

(16)

where $x_\text {r} = x_\text {m} - x_\text {c}$ and $v_\text {r} = \dot{x}_\text {m} - \dot{x}_\text {c}$ are the relative displacement and velocity, respectively, between the magnetic inner mass and the capsule shell.

Driven by $F_\text {i}$, the capsule shell may move either forward or backward, which is subjected to the reaction from the small intestine including $F_x$ and Coulomb friction, $F_\text {f}$. Depending on the moving speed and the other forces, the frictional force is given by

$$\begin{aligned} F_\text {f} = {\left\{ \begin{array}{ll} -{{\,\mathrm{sign}\,}}(\dot{x}_\text {c}) \mu G, &{} \text {if } \dot{x}_\text {c} \ne 0, \\ -{{\,\mathrm{sign}\,}}(F_\text {i} + F_x) \mu G, &{} \text {if } \dot{x}_\text {c}=0 \text { and } \text {abs}\left( F_\text {i} + F_x \right) \ge \mu G, \\ -F_\text {i} - F_x, &{} \text {if } \dot{x}_\text {c}=0 \text { and } \text {abs}\left( F_\text {i} + F_x \right) < \mu G, \end{array}\right. } \end{aligned}$$

(17)

where ${{\,\mathrm{sign}\,}}(*)$ and $\text {abs}(*)$ return the sign and absolute values of $*$, and $\mu$ is the frictional coefficient, respectively. Here, it is worth noting that Coulomb friction has been verified experimentally in [16] that it is sufficient to depict the friction between the capsule and the small intestine. Given all of the forces and free-body diagram in Fig. 3c, the governing equations of the capsule dynamics are written as

$$\begin{aligned} {\left\{ \begin{array}{ll} m_\text {m} \ddot{x}_\text {m} = F_\text {e} - F_\text {i},\\ m_\text {c} \ddot{x}_\text {c} = F_\text {i} + F_x + F_\text {f}. \end{array}\right. } \end{aligned}$$

(18)

It is worth noting that $F_x$ in Eq. (18) is the horizontal reaction force exerted by the small intestine and the fold on the capsule. It can be calculated numerically by solving Eqs. (12), (13), and (14).

3 Bifurcation analysis

The model, Eq. (18), involves many parameters influencing the capsule response moving in the small intestine and engaged with the circular fold. It is impossible to go through all the parameter values, but bifurcation analysis can be performed based on our primary studies, which proposed a millimetre-scale capsule moving in the small intestine [17], and investigated the intestinal friction on the capsule in various capsule-intestine contacts [16]. Given these two works, the default selection of the system parameters is listed in Table 1.

Table 1 Default parameter values for the bifurcation analysis (obtained from [16, 17])

For the bifurcation analysis, Rung-Kutta method was used to numerically solve Eq. (18), with the transient phase omitted for steady state. In general, simulation was performed for 100 excitation periods, and the last 10 periods were used to construct the bifurcation diagrams. For complex responses with more than 10 periods, the simulation was extended accordingly. Because the numerical simulations were very time-consuming, a relative large interval of 1 mN was firstly used to construct the bifurcation diagrams. Then, a small interval of 0.2 mN was adopted to improve the resolution in the vicinities of bifurcation points and of the regions with multiple stabilities. In each excitation period, the minimum magnet-capsule relative velocity, $\text {min}(v_\text {r})$, was recorded as the Poincaré section, and the excitation amplitude was used as the bifurcation parameter. In addition, we used the abbreviation, P-l-m-n, to denote the nonlinear response of period-l motion with m left impacts and n right impacts.

Fig. 4

(Colour online) Critical excitation amplitudes for the capsule to cross the circular fold, with the duty cycle and excitation period selected for $D\in [10\%, 90\%]$ and $T\in [0.01,0.09]$ s, respectively

3.1 Influence of the excitation amplitude

In this work, we are interested in the steady-state response when the capsule is engaged with the circular fold, and it is critical to know the capsule’s progression in the presence of the fold. As seen in Fig. 4, this criticality is determined by the driving force, showing that a large excitation amplitude is required for the capsule to cross the fold. In addition, it is seen that a 50 mN excitation force is sufficient for the fold crossing when the duty cycle is large enough, $D>30\%$, while a small duty cycle ($D=10\%$) may requires up to 100 mN force. By contrast, the influence of excitation period, T, on the fold crossing is not as significant as the duty cycle. Except the line of a very short period, $T=0.01$ s, which requires relatively larger force for the crossing, other excitation periods yield very similar results.

To illustrate the capsule response before fold crossing, the bifurcation diagram for $D = 40\%$ and $T=0.05$ s is displayed in Fig. 5 as an example, with the time series of displacements of the inner mass and capsule shell, and the phase portraits of the relative displacement and velocity plotted for some typical responses. For a small driving force, $P_\text {d}\le 11.8$ mN, as illustrated in Fig. 5b, the capsule performs a P-1-3-0 response, i.e., period-1 motion with three left impacts and without any right impact. Then a periodic doubling occurs for $P_\text {d}=12$ mN, yielding a P-2-5-0 motion for $P_\text {d}=\in [12, 14.1]$ mN. Then a reverse periodic doubling results in P-1-2-0 motion for $P_\text {d}=[14.6,16.6]$ mN. For $P_\text {d}=16.6$ mN, a grazing bifurcation occurs, inducing a P-1-1-0 motion co-existing with the P-1-2-0 response which suddenly disappears thereafter. Then the P-1-1-0 motion lasts until it changes into quasi-periodic before the capsule crosses the fold for $P_\text {d}>26$ mN. To illustrate, the time series of the capsule and inner mass for $P_\text {d}=27$ mN are displayed in Fig. 5g, where the regions enclosed by the dashed lines AB (marked by yellow background) and CD denote the head-fold and tail-fold contacts, respectively. As seen, the capsule motion is decreased by the fold once it enters the yellow region, which is re-accelerated from $t>0.25$ s when the capsule stands on the top of the fold.

Fig. 5

(Colour online) a Bifurcation diagram of the minimum relative velocities plotted as a function of the excitation amplitude, for $D=40\%$. Grey region indicates the case of fold crossing. Additional windows demonstrate the trajectories on the phase plane ($x_\mathrm {r}$, $v_\mathrm {r}$) and the time histories of inner mass and capsule’s displacements (denoted by blue and red lines, respectively) obtained for b $P_\mathrm {d}=9$ mN, c $P_\mathrm {d}=13$ mN, d, f $P_\mathrm {d}=16.6$ mN, and e $P_\mathrm {d}=26$ mN. g Time series for $P_\mathrm {d}=16.6$ mN, where the regions enclosed by the dashed lines AB (marked by yellow background) and CD denote the head-fold and tail-fold contacts, respectively. The locations of the left impact surface are shown by vertical dashed lines, and Poincaré sections on the phase plane are marked by red dots

3.2 Influence of the capsule design

With respect to the increase of the inner mass, $m_\text {m}$, from 1 g to 2.5 g, as seen in Fig. 6, the bifurcation pattern becomes more complex, and the required excitation amplitude for crossing becomes larger. In Figs. 6a for $m_\text {m}=1.5$ g, the capsule response is always P-1-2-0, where the crossing occurs when $P_\text {d}>21$ mN. For $m_\text {m}=2$ g, as seen in Fig. 6b, the P-1-2-0 motion is changed into quasi-periodic for $P_\text {d}=16.9$ mN, which is transformed into P-3-1-0 motion for $P_\text {d}=17.5$ mN. The motion becomes P-4-1-0 for $P_\text {d}=20.5$ mN, which is then changed into P-1-0-0 for $P_\text {d}>20.7$ mN until the crossing occurs at $P_\text {d}=22$ mN. The bifurcation pattern is even more complex for $m_\text {m}=2.5$ g in Fig. 6c, showing three regions of non-periodic motion for $P_\text {d}\in [15.3,15.9]$ mN, $P_\text {d}=16.9$ mN and $P_\text {d}\in [19.1,19.5]$ mN dividing the regions for P-1-2-0, P-5-3-0, P-3-1-0, and P-1-0-0 motions. The period-1 response is then kept with respect to the increase of $P_\text {d}$ before the capsule crosses the fold for $P_\text {d}>22.9$ mN.

Fig. 6

Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $m_\text {m}$=1.5 g, b $m_\text {m}$=2 g, and c $m_\text {m}$=2.5 g. Grey regions indicate the cases of fold crossing

Increasing the capsule mass, $m_\text {c}$, as displayed in Fig. 7, also complicates the bifurcation pattern and delays the occurrence of fold crossing. With a small capsule mass, Figs. 7a and b illustrate a region of P-1-3-0 motion for a small excitation amplitude, which is then transformed into P-1-2-0 motion by increasing either $m_\text {c}$ or $P_\text {d}$. For $m_\text {c}=1$ g, the P-1-2-0 response is kept until the excitation is strong enough, $P_\text {d}>20$ mN, to drive the capsule to climb over the fold. For $m_\text {c}=1.5$ g, the P-1-2-0 motion suddenly disappears for $P_\text {d}=18.7$ mN, with a P-2-1-0 response showing up for $P_\text {d}>16.9$ mN to co-exist with it. The P-2-1-0 motion is then transformed into P-3-1-0 for $P_\text {d}\in [19.9,20.1]$ mN, which becomes quasi-periodic for $P_\text {d}\in [20.3,20.9]$ mN. Before the capsule crosses the fold, P-1-0-0 motion shows up for $P_\text {d}>20.9$ mN. Compared with Fig. 7b, the bifurcation diagram in Fig. 7c for $m_\text {c}=2.5$ g is much different. Two regions for non-periodic motions for $P_\text {d}\in [16.9, 17.3]$ mN and $P_\text {d}\in [18.1, 18.9]$ mN divide the P-1-2-0, P-3-5-0 and P-2-3-0 motions without any sudden jumps. In addition, the region for $P_\text {d}\in [19.7, 22.3]$ mN witnesses an isolated branch of P-1-1-0 response coexisting with the P-2-3-0 motion. Finally, the fold crossing is realised by a quasi-periodic response for $P_\text {d}>22.9$ mN, instead of the period-1 motions.

Fig. 7

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $m_\text {c}=1$ g, b $m_\text {c}=1.5$ g, and c $m_\text {c}=2.5$ g. Blue diamonds and grey regions indicate the coexisting attractors and the cases of fold crossing, respectively

In Fig. 8, it is seen that increasing the stiffness, k, also complicates the bifurcation pattern, but it has inapparent influence on the critical excitation amplitude for fold crossing, which occurs for $P_\text {d} \approx 22$ mN. For $k=50$ $\text {N m}^{-1}$ in Fig. 8a, the P-1-2-0 motion is successively transformed into P-4-4-0, P-2-3-0, P-3-2-0, P-2-3-0, P-3-1-0, quasi-periodic and P-1-1-0 response for $P_\text {d}= 15.5$, 15.7, 16.1, 16.3, 16.7, 18.5, and 18.9 mN, respectively. For $k=100$ N/m in Fig. 8b, there exists a region for P-1-3-0 motion when the excitation amplitude is small, which is changed into P-1-2-0 for $P_\text {d}>11$ mN. It is then changed into P-2-4-0 response for $P_\text {d}\in [20.9, 21.1]$ mN to co-exist with a P-2-2-0 motion. The P-2-2-0 response is kept before crossing occurs at $P_\text {d}>22.3$ mN by a P-4-5-0 motion. Moreover, it can be seen in Fig. 8c that further increase of k makes the nonlinear responses even more plentiful. Without any co-existing attractors, Fig. 8c shows nine different periodic motions and three isolated regions for non-periodic responses until the fold is crossed at $P_\text {d}>22.3$ mN.

Fig. 8

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $k=50$ [$\text {N m}^{-1}$], b $k=100$ [$\text {N m}^{-1}$], and c $k=200$ [$\text {N m}^{-1}$]. Blue diamonds and grey regions indicate the coexisting attractors and the cases of fold crossing, respectively

By contrast, alternating the stiffness $k_2$ between $20\times 10^3$ N/m and $40\times 10^3$ N/m, which is much stiffer compared with k, as seen in Fig. 9, does not have a significant influence on the bifurcation pattern. As an example, the P-1-2-0 motion shown in Fig. 9b disappears at $P_\text {d}>18.5$ mN. Before that, it co-exists with the P-2-1-0 and P-4-2-0 motions for $P_\text {d}\in [17.5, 17.7]$ mN and $P_\text {d}\in [17.9, 18.5]$ mN, respectively. Thereafter, a mono-stability of P-3-1-0 shows up for $P_\text {d}\in [18.7, 20.5]$ mN, which becomes non-periodic for $P_\text {d}\in [20.7, 21.1]$ mN. Then the P-1-0-0 motion turns up again before the fold crossing occurs at $P_\text {d}>21.5$ mN.

Fig. 9

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $k_2=20\times 10^3$ N/m, and b $k_2=40\times 10^3$ N/m. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

In Fig. 10, it is seen that increasing the damping, c, simplifies the bifurcation pattern, but hardly influences the critical excitation amplitude for fold crossing. In Fig. 10a, the P-1-2-0 motion for weak excitation disappears at $P_\text {d}=18.1$ mN, which co-exists with the quasi-periodic, P-5-3-0, and P-2-1-0 motions for $P_\text {d}=17.3$, $P_\text {d}\in [17.5,17.7]$, and $P_\text {d}\in [17.9,18.1]$ mN, respectively. The P-2-1-0 motion is then changed into a quasi-periodic response for $P_\text {d}=19.3$ mN. Afterwards, two more regions of quasi-periodic motions for $P_\text {d}=19.9$ and $P_\text {d}\in [20.5, 20.9]$ mN show up to divide the regions of P-3-1-0 and P-1-0-0 motions. Finally, the fold crossing occurs at $P_\text {d}=21.7$ mN by the P-1-0-0 motion. The pattern in Fig. 10b for $c=0.04$ Ns/m is similar to that in Fig. 10a, but has less changes in the response after the disappearance of P-1-2-0 motion for $P_\text {d}=17.1$ mN. The bifurcation diagram in Fig. 10c for $c=0.08$ Ns/m is much simpler than the previous two, without change in the number of period or any co-existing attractors. It is always period-1, but has less number of left impacts with respect to the enhancement of excitation amplitude.

Fig. 10

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $c=0.02$ Ns/m, b $c=0.04$ Ns/m, and c $c=0.08$ Ns/m. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

Influence of the right gap, $g_1$, is illustrated in Fig. 11. When the gap is sufficient large, $g_1>0.4$ mm, as seen in Fig. 11c, the inner mass hardly touches the right spring, showing a bifurcation pattern similar to those discussed in Fig. 9, which is P-1-2-0 for small excitation amplitude and jumps to be irregular and P-3-1-0 for large $P_\text {d}$ before the fold crossing. When the gap is decreased to 0.3 mm, as seen in Fig. 11b, the responses with several right impacts, which are not observed in any other cases, show up for large excitation amplitude. Meanwhile, the fold crossing is delayed from $P_\text {d}=21$ mN to 22 mN, and the multiple stability disappears. In Fig. 11a, the gap is further reduced to 0.1 mm, resulting in a very simple bifurcation pattern, which is P-1-2-5 and irregular for small and large excitation, respectively. However, due to the frequent right impact, the corresponding phase portrait in Fig. 11d is much more complex compared with those in Figs 11e and f.

Fig. 11

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $g_1=0.1$ mm, b $g_1=0.3$ mm, and c $g_1=0.5$ mm, with the phase portraits for $P_\text {d}=20$ mN displayed in d–f. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

Fig. 12

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $L=10$ mm, and b $L=20$ mm. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

It is seen in Fig. 12 that the bifurcation pattern and the critical excitation amplitude for the fold crossing are insensitive to the variation of the capsule length, L. All bifurcation diagrams are very similar to the one displayed in Fig. 13c for $R=6$ mm. By contrast, increasing the capsule radius, R, from 4 to 7 mm, as seen in Fig. 13, complicates the bifurcation after the disappearance of the P-1-2-0 motion, and slightly reduces the critical excitation amplitude for the fold crossing from $P_\text {d} = 22.1$ to 20.9 mN. In Fig. 13a for $R=4$ mm, there are two regions of quasi-periodic motion for $P_\text {d} \in [17.7, 18.7]$ mN and $P_\text {d} \in [19.5, 20.1]$ mN dividing the regions of P-2-1-0, P-3-1-0 and P-1-0-0 motions, and the crossing is realised by the P-1-0-0 motion. In Fig. 13d for $R=7$ mm, by contrast, there are four regions of quasi-periodic response dividing the regions of P-2-1-0, P-5-3-0, P-4-2-0 and P-3-1-0 motions, and the fold crossing follows a quasi-periodic response.

Fig. 13

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $R=4$ mm, b $R=5$ mm, c $R=6$ mm, and d $R=7$ mm. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

3.3 Influence of the small intestine and the circular fold

With respect to the increase of the intestine thickness, H, from 1 to 2 mm, as seen in Fig. 14, the bifurcation diagram is gradually simplified, but the critical excitation amplitude for the fold crossing is unchanged. In Fig. 14a, the P-1-2-0 motion suddenly disappears for $P_\text {d}=18.3$ mN, before which there co-exists a quasi-periodic motion for $P_\text {d}\ge 17.9$ mN. The quasi-periodic response lasts until $P_\text {d}=18.9$ mN, where it is changed into a P-2-1-0 motion which undergoes a periodic-doubling bifurcation to be P-4-2-0 for $P_\text {d}\in [19.3,19.9]$ mN. It is then transformed into P-3-1-0 at $P_\text {d}\ge 20.1$ mN, and finally bifurcated into quasi-periodic again before the crossing occurs at $P_\text {d}>21.5$ mN. For $H=1.5$ mm in Fig. 14b, there is no co-existing attractors near the disappearance of P-1-2-0 motion. It directly bifurcates into quasi-periodic at $P_\text {d}\ge 18.1$ mN, which is then transformed into quasi-periodic at $P_\text {d}\ge 18.5$ mN. This motion lasts until the fold crossing occurs for $P_\text {d}>21.5$ mN. Then thickness is further increased to 2 mm, as displayed in Fig. 14c, the bifurcation pattern becomes much simpler. The P-1-2-0 motion becomes quasi-periodic for $P_\text {d}\ge 18.5$ mN, which is kept until the capsule crosses the fold for $P_\text {d}>21.5$ mN.

Fig. 14

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $H=1$ mm, b $H=1.5$ mm, and c $H=2$ mm. Blue diamonds and grey regions indicate the coexisting attractors and the cases of fold crossing, respectively

By contrast, as shown in Fig. 15, increasing the frictional coefficient, $\mu$, from 0.2 to 0.3, delays the fold crossing while simplifies the bifurcation pattern. For $\mu =0.2$ in Fig. 15a, the P-1-2-0 motion disappears with a very small driven force, $P_\text {d}>7.9$ mN, yielding a co-existing quasi-periodic attractor for $P_\text {d}=7.9$ mN. Then one observes a frequent change of the response with respect to the increase of $P_\text {d}$, including P-2-1-0, P-4-2-0, P-3-1-0 and quasi-periodic motions. It finally stays at P-1-0-0 for $P_\text {d}\ge 9.5$ mN, which lasts until the fold crossing occurs for $P_\text {d}>15$ mN. In Fig. 15b, increasing $\mu$ to 0.2 yields a similar bifurcation pattern compared with Fig. 15a, but it requires a much larger driven force to trigger off both of the bifurcation and fold crossing. When $\mu$ is further increased to 0.3, as seen in Fig. 15c, the P-1-2-0 motion lasts until the fold crossing for $P_\text {d}>24$ mN, without incurring any bifurcation in the nonlinear response.

Fig. 15

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $\mu =0.1$, b $\mu =0.2$, and c $\mu =0.3$. Blue diamonds and grey regions indicate the coexisting attractors and the cases of fold crossing, respectively

Changing the mechanical property of the small intestine can result in very complex dynamics of the capsule. To illustrate, the bifurcation diagram for $E=75$ kPa is displayed in Fig. 16a, showing the co-existence of three stable attractors for $P_\text {d}\in [19.1, 20.1]$ mN. If only the attractor marked by red dots is tracked, one can find a simple bifurcation pattern, switching between the P-1-2-0 and P-2-4-0 motions via periodic doubling and reverse periodic doubling at $P_\text {d}=13.9$ mN and 17.9 mN. However, there exists another branch of P-2-4-0 motion (denoted by blue diamonds) for $P_\text {d}\in [19.1, 20.1]$ mN connecting the P-1-2-0 branch. In addition, there is a third isolated branch (marked by orange circles) for $P_\text {d}\in [17.3, 20.3]$ mN, which alternates among quasi-periodic, P-1-1-0, P-2-2-0, P-2-4-0, and P-3-2-0 responses. Time series and phases portraits of the typical responses, including the co-existing attractors, are plotted in the additional windows of Fig. 16. Yellow regions in the time series indicate the interaction between the capsule head and the fold, showing that a small excitation amplitude, $P_\text {d}<22.1$ mN, cannot drive the capsule to climb up the fold.

Fig. 16

(Colour online) a Bifurcation diagram of the minimum relative velocities plotted as a function of the excitation amplitude for $E=75$ kPa. Blue diamonds and orange circles represent the co-existing attractors, and grey regions indicate the cases of fold crossing. Additional windows demonstrate the trajectories on the phase plane ($x_\mathrm {r}$, $v_\mathrm {r}$) and the time histories of inner mass and capsule’s displacements (denoted by blue and red lines, respectively) obtained for b $P_\text {d}=10$ mN, c, f 17.7 mN, d, g 18.7 mN, e, h 19.9 mN, and i 20.3 mN. j Time series for $P_\mathrm {d}=23$ mN, where the regions enclosed by the dashed lines AB and CD denote the head-fold and tail-fold contacts, respectively. The locations of the left impact surface are shown by vertical dashed lines, and Poincaré sections on the phase plane are marked by red dots, blue diamonds, and orange circles

Either increasing or decreasing the stiffness of the small intestine, as seen in Fig. 17, can simplify the bifurcation pattern. A softer tissue, $E=25$ kPa in Fig. 17a, yields a pattern similar to some of the previous bifurcation diagrams, such as the one in Fig. 13c. By contrast, a stiffer tissue, $E=100$ kPa in Fig. 17b, results in a new pattern, which has one extra region of bi-stability for $P_\text {d}\in [20.1, 20.3]$ mN. Moreover, it can be seen from Figs. 16 and 17b that a large tissue stiffness changes the capsule response back to the P-1-2-0 motion before the fold crossing, which is not observed in any other cases.

Fig. 17

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $E=25$ kPa, and b $E=100$ kPa. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

As displayed in Fig. 18, the critical excitation amplitude increases from 17 to 24.1 mN when the fold height grows from 1 to 2.5 mm. Thus, a higher fold requires a larger driving force to climb over. For a shorter fold in Fig. 18a, the P-1-2-0 lasts without any qualitative change. In case that $h=1.5$ mm, as seen in Fig. 18b, the P-1-2-0 motion disappears at $P_\text {d}>18.1$ mN, with quasi-periodic and P-2-1-0 motions co-existing for $P_\text {d}=17.9$ and 18.1 mN, respectively. It is then successively bifurcated into P-5-3-0, P-4-2-0, and P-3-1-0 for $P_\text {d}\in [18.5, 18.9]$ mN, $P_\text {d}\in [19.1, 20.3]$ mN and $P_\text {d}\in [20.7, 21.1]$ mN, respectively, followed by a quasi-periodic motion occurs at $P_\text {d}=21.3$ mN, right before the fold crossing. For $h=2.5$ mm in Fig. 18c, one can observe a reverse periodic doubling from P-2-2-0 to P-1-1-0 at $P_\text {d}=21.1$ mN, after the disappearance of P-1-2-0 motion for $P_\text {d}>19.1$ mN. Finally, the fold crossing is also realised by a quasi-periodic response.

Fig. 18

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $h=1$ mm, b $h=1.5$ mm, and c $h=2.5$ mm. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

With respect to the increase of the fold width, w, from 1 to 3 mm, as seen in Fig. 19, the bifurcation pattern is complicated, while the critical excitation amplitude for the crossing is slightly reduced from 21.7 to 21.1 mN. For $w=1$ mm in Fig. 19a, the P-1-2-0 motion disappears for $P_\text {d}>18.1$ mN, where a quasi-periodic response co-exists. Thereafter, there is only a P-2-1-0 motion lasting until the capsule crosses the fold for $P_\text {d}>21.7$ mN. Once increasing the fold width, the bifurcation after the disappearance of the P-1-2-0 motion becomes much more complex. To illustrate, the P-2-1-0 response in Fig. 19c bifurcates into a P-3-1-0 motion for $P_\text {d}>18.5$ mN, which is then transformed into quasi-periodic again for $P_\text {d}>20.3$ mN. This quasi-periodic response is then kept until the fold crossing for $P_\text {d}>21.1$ mN.

Fig. 19

(Colour online) Bifurcation diagrams of the minimum relative velocities plotted as functions of the excitation amplitude, for a $w=1$ mm, b $w=1.5$ mm, and c $w=3$ mm. Blue diamonds and grey regions indicate the co-existing attractors and the cases of fold crossing, respectively

4 Conclusions

A vibro-impact capsule moving on the small intestine substrate with a circular fold has been mathematically modelled in this paper, and its dynamic response has been studied by bifurcation analysis. Influences of various parameters, such as the amplitude, period and duty cycle of the external driving force, the mass, stiffness, damping and geometries of the capsule, the mechanical properties and geometries of the tissue and the circular fold, on the capsule dynamics have been studied. A general trend of dynamics of the capsule system has been found. It shows that the capsule always performs a period-1 motion when the excitation amplitude is small, while the crossing of the circular fold requires a strong excitation, especially when the duty cycle is too small. In addition, it has also been found that the secondary spring of the capsule has no influence on the capsule dynamics, since the right gap is too large and the inner mass cannot contact with the right constraint.

Our studies indicated that some parameters, such as the stiffness of the secondary and the tertiary springs, and the capsule length, can hardly influence the capsule response and the critical excitation amplitude required for fold crossing. For the fold crossing, it was found that increasing the inner mass, capsule mass, frictional coefficient, or the fold height can significantly delay the occurrence of crossing, while the other parameters, such as the damping, stiffness of the primary spring, capsule radius, intestine thickness and Young’s modulus, and the fold width, have very limited influence on the required force for fold crossing. In general, it was found that the capsule has a large probability to perform the P-1-0-0 and the quasi-periodic motions right before the fold crossing.

For the bifurcation pattern, the P-1-2-0 response is very typical when the driving force is small, except for some special cases, such as a light inner mass or a large stiffness of the primary spring, which may lead to a P-1-3-0 response. Decreasing the inner mass or the capsule mass, or increasing the frictional coefficient can reduce the bifurcation of the nonlinear capsule, so keeps the P-1-2-0 motion until the fold crossing occurs. On the contrary, increasing the Young’s modulus of the tissue yields very complex bifurcations, including the co-existence of three stable attractors. Moreover, we found a very unique phenomenon due to the large Young’s modulus that, the response of the capsule can be changed back to the P-1-2-0 motion before the fold crossing, even if it undergoes many complex bifurcations with respect to the increase of the driving force, which was not observed in any other cases.