1 Introduction

Pendulum-like systems are commonly used in many practical applications, including special dynamical dampers or energy harvesters [1]. Dynamics of such systems can exhibit extremely complex behaviour. Especially, if the system is nonlinear and includes the inertial coupling, among strange attractors, multiple regular attractors may co-exist for some values of system parameters [2]. The presence of the coupling terms can lead to a certain type of instability which is referred to as autoparametric resonance. This kind of phenomenon takes place when the external resonance and the internal resonance meet themselves, due to the coupling terms. The multiple solutions, evolution of the solution due to variations in parameters or initial conditions play a very important role in system dynamics. The small perturbation of initial conditions or systems parameters may transit the response to dangerous motion, like a full rotation of the pendulum or chaotic motion [3]. This problem is essential if the pendulum plays role of a dynamical vibration absorber or the energy harvesting device [4]. An autoparametric system has been intensively analysed for three last decades. The different responses in the autoparametric pendulum vibration absorber for a linear mass-spring damper system have been studied by the harmonic balance method in Hatwal et al. [5]. A nonlinear frequency analysis using the multiple scales method has been presented in Cartmell et al. [6, 7]. The two mode autoparametric interaction and robustness, against variations on the excitation frequency, are improved on the overall system by direct application of an on–off servomechanism, controlling the effective pendulum length and validating also the theoretical results in an experimental setup. A similar pendulum dynamic vibration absorber, with time delay in the internal feedback force, is used to illustrate the real-time application of a dynamic substructuring technique in Kyrichko et al. [8] and in paper [9].

In this paper authors propose application of the MR damper, installed between the oscillator and the ground to provide controllable damping for the system. The model of a damper takes into account the hysteretic effect. The closed-loop control algorithms offer possibility to move the system between selected stable solutions. Moreover, we show, that MR damping practically does not reduce the vibration suppression effect and MR damping can cause a shift of chaotic regions.

2 An autoparametric pendulum system

2.1 Model of magnetorheological damper (MRD)

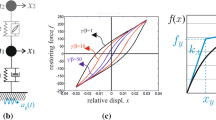
The magnetorheological devices provide modern and elegant solutions for semi-active control in a variety of applications, offering several advantages: simplicity of a structure, small number of mobile components, noise-free fast operation and low power demands. The MRD is a nonlinear component with dissipative capability used in the control of semi-active suspensions, where the damping coefficient varies according to the applied electric current. MR damper is usually characterized by the displacement and/or velocity of the piston, the electric current applied to the coil as inputs and the force generated on the piston as output. The relationship between damping force and velocity shows hysteresis loops whose shapes vary according to the applied current. Hysteresis in dampers is due to the difference between the accelerating and decelerating paths of the force-velocity curve [10], thus imposing a delay in the changes of internal pressures and ultimately forces. Therefore, we propose the nonlinear MR damping force (F MR ) approximated by a hyperbolic tangential function of the velocity and the displacement of the oscillator based on the papers [11, 12]. In terms of mathematical expressions, the model makes use of a hyperbolic tangent function to represent the hysteresis and linear function to represent the viscous behaviour

$$ F_{MR}=\alpha_1 \dot{X}+\alpha_3 \tanh{(e_1 \dot{X}+e_2 X)} $$
(1)

where α 1 means viscous damping parameter, i.e. the slope of linear part of Eq. 1, α 3 indicates dry friction, i.e. height of hysteretic loop, e 1 describe the slope shape of dry friction and e 2 denotes the width of a hysteretic loop. The influence of parameters of Eq. 1 on the hysteretic loop shape and comparison with the classical viscous damping (α 3 = 0) and with the model without hysteresis (e 2 = 0) are presented in Fig. 1.

Fig. 1
figure 1

Attitiude of MR damper in force-velocity curves, α 1 = 0.1

Full size image

Based on experimental and numerical studies, the relationship between e 1/e 2 approximately equals 10. If the parameter e 2 equals zero then we have the MR damper without the hysteretic effect. This model was studied in paper [4]. If the parameter α 3 equals zero, then we obtained classical viscous damping model widely used in the literature.

2.2 Model of an autoparametric pendulum system (APS)

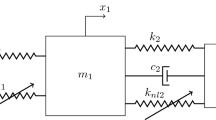
Autoparametric vibration systems have an interesting dynamics that results from at least two nonlinear subsystems coupled to interact in a way where one of them transfers the exogenous perturbation energy to the other. This type of structures as vibration absorber dampers are applied in technique [13]. The scheme of an autoparametric vibration absorber system is shown in Fig. 2. A pendulum vibration absorber is attached to the damped oscillator. The oscillator suspension is considered as a classical linear suspension with viscous damping or nonlinear suspension with a nonlinear spring (Duffing characteristic) and a magnetorheological damper.

Fig. 2
figure 2

Scheme of the autoparametric pendulum vibration absorber

Full size image

The equations of motion for the two degrees-of-freedom APS are described by dimensionless form [4]:

$$ \ddot{X}+F_{MR}(\dot{X},X)+F_S(X)+\mu \lambda({\ddot{\varphi}}\sin \varphi+\dot{\varphi}^2 \cos \varphi)=q \cos(\vartheta \tau) $$
(2)
$$ \ddot{\varphi}+\alpha_2 \dot{\varphi}+\lambda(\ddot{X}+1)\sin{\varphi}=0 $$
(3)

where Fs denotes function of stiffness oscillator spring

$$ F_S(X)=X+\gamma X^3 $$
(4)

where γ is a dimensionless stiffness coefficient. The motion of the APS is described by two generalized coordinates namely the displacement of the oscillator in the vertical direction X, and the angle of the pendulum rotation \(\varphi. \) The parameters μ and λ in Eqs. 2 and 3 describe the parameters of the pendulum (the length and mass of the pendulum as a function natural frequency and static displacement of the linear oscillator [14]). The parameter α 2 denotes the dimensionless damping in the pendulum pivot, assumed to be constant. The frequency and amplitude of harmonic excitation are denoted as ϑ and q, respectively.

3 Regular motion under MR damping influence

3.1 Influence MR damping on main parametric resonance and stability

Active and semi-active control provides an important new tool for a control engineer. The MR damper behaviour can be modified from viscous effects, if the system is not activated, to a mixed mode system with viscous and dry friction components, when the damper is activated. Variable MR force (F MR ) gives possibility to on-line control and improve dynamics of an autoparametric system (Fig. 2). However, to get the desired response, it is necessary to know influence the MR damping when the system operates in regular or chaotic zones. First, let us analyse the influence of magnetorheological damping on stability of resonance curves. Our calculations have been performed using software for numerical continuation Auto07p [15]. Similar software for system with the pendulum has been used in [16, 17]. The simulation data were taken from [4]: α 1 = 0.1, α 2 = 0.02, μ = 6, λ = 0.3, q = 0.2, γ = 0 and e 1 = 10, e 2 = 1. Initial conditions are fixed as: \(X(0)=0, \dot{X}(0)=0, \varphi{(0)}=0.1\) and \(\dot\varphi{(0)}=0. \)

The resonance curves for the oscillator and the pendulum for a system with classical viscous damping is presented in Fig. 3. The case of response with a fixed, not oscillating pendulum is marked by the black line. This type of solution is called semi-trivial solution (ST). While the red line corresponds to the case where the pendulum swings [called non-trivial solution (NT)]. When the pendulum and the oscillator are in a rest (equilibrium position), the case is called trivial solution (T). The unstable solutions are marked by dash-dotted line, while the solid line denotes stable solutions. Close to ϑ ≈ 1.05, the dynamical elimination of oscillator’s vibration caused by the pendulum swinging is clearly visible.

Fig. 3
figure 3

Frequency response for the oscillator (a) and the pendulum (b), for α 3 = 0, obtained by continuation method

Full size image

The continuation reveals that for small range of parameters, two stable non-trivial solutions exist. The situation takes place for frequency of excitation ϑ = 0.9 (Fig. 3b). This case will be studied and explained in the next part of the paper. These solutions represent pendulum swings, with shifted centre of vibration (positive or negative). Therefore, in Fig. 3a only one NT solution is observed. The oscillator vibrates with the same amplitudes, either for positive or negative shift of the pendulum. This result will be used in the next paragraph to control and jump from one solution to another with a help of the MR damper. [b]

Introducing MR damping, we reduced the amplitude of the oscillator (Figs. 4a, 5a) and the pendulum (Figs. 4b, 5b), but the absorption effect still exists (even, for the large values of parameters α 3 = 0.1, Fig. 5a). This is a very important effect from a practical point of view, because this parameter can be used to control dynamics of the vibration absorber without decrease its efficiency. Moreover, the damping analysis shows, that the increase of MR damping, decreases the resonance region in a small extent.

Fig. 4
figure 4

Frequency response for the oscillator (a) and the pendulum (b), for α 3 = 0.05, obtained by the continuation method

Full size image
Fig. 5
figure 5

Frequency response for the oscillator (a) and the pendulum (b), for α 3 = 0.1, obtained by the continuation method

Full size image

The influence of MR damping on the amplitude of the oscillator and the pendulum is shown in Fig. 6. The bifurcation diagrams are made by one parameter continuation method for fixed frequency of excitation, near the dynamic absorption effect (ϑ = 1). The critical value of MR damping for the pendulum swinging is equal to α cr  = α 3 = 0.13 (Fig. 6b).

Fig. 6
figure 6

Bifurcation diagram: α 3 versus maximal amplitude of the oscillator (a) and the pendulum (b) for ϑ = 1, obtained by continuation method

Full size image

Interestingly, that the increase of parameter α 3 causes slight growth of the amplitude of oscillator (Fig. 6a). This is due to the fact that the suppression effect is slightly worsened. The oscillator reaches the maximal amplitude in bifurcation point where the NT changes into ST solution. If the value exceeds α cr , the amplitude of pendulum reaches zero and its motion vanishes. Then, the pendulum plays just a role of additional mass of the oscillator.

3.2 Pendulum swings control

An autoparametric system can display in resonance condition different behaviours including periodic, quasi-periodic, non-periodic and also chaotic [18]. Moreover, the occurrence the resonance often goes along with the saturation phenomena [19]. Therefore, the control dynamics and tuning are important in such systems. Due to the fact, that both subsystems in such systems are coupled by inertial term, the control of the pendulum motion by damper mounted in the suspension is very difficult.

The parametric damping analysis presented in [20], showed that the increase of pendulum damping significantly reduced or even eliminated the dynamic vibration absorption phenomenon. While the increased of the oscillator damping only insignificantly reduced the absorption effect. Therefore, the control of an autoparametric system by oscillator damping looks promising from a vibration suppression effect point of view.

The bifurcation diagrams of the oscillator (Fig. 7a) and the pendulum (Fig. 7b) show that different responses are possible. We can see that, for value about α 3 < 0.025 two stable periodic solutions of the pendulum exist (marked as solution nos. 2 and 3 in Fig. 7b), but only one for the oscillator (Fig. 7a). These solutions nos. 2 and 3 represent the pendulum swinging where the pendulum’s vibration centre is shifted (Figs. 10a, 11a, for τ < 1,000). Depending on the initial conditions the centre of the swinging may be shifted in the positive (Fig. 10a, solution no. 2) or the negative (Fig. 11a, solution no. 3) direction. Of course, the two possible shifts are symmetric around the lower static position of the pendulum. If the MR damping is located between α 3 = 0.025 and α 3 = 0.07, then we observe only one stable pendulum non-trivial solution (no. 1). The ST solution is denoted as solution no. 0.

Fig. 7
figure 7

Bifurcation diagram: MR damping versus the maximal amplitude of the oscillator (a) and the pendulum (b) for ϑ = 0.88, obtained by continuation method

Full size image
Fig. 8
figure 8

Basins of attraction of the pendulum: ϑ = 0.88, α 3 = 0.01 (a), α 3 = 0.05 (b)

Full size image
Fig. 9
figure 9

Scheme of control algorithm dedicated to jump from attractor no. 2 into 3 or vice versa

Full size image
Fig. 10
figure 10

Time histories of the pendulum (a) and the oscillator (b) during the jump from the solution no. 3 into 2 for fixed frequency ϑ = 0.88 with applied control algorithm

Full size image
Fig. 11
figure 11

Time histories of the pendulum (a) and the oscillator (b) during the jump from solution no. 2 into 3 for fixed frequency ϑ = 0.88 with applied control algorithm

Full size image

To verify bifurcation diagrams, the basin of attraction have also to have been done (Fig. 8). The basins of attraction have been performed using the Dynamics package [21]. In Fig. 8a we observe two possible NT stable solutions represented by double-point attractors no. 2 with the pink colour basins of attraction (corresponding solution no. 2 in Fig. 7b) and double-point attractor no. 3 with the grey colour basins of attraction (corresponding solution no. 3 in Fig. 7b). The semi-trivial solution is represented by attractor no. 0, with the blue colour basins of attractor. These basins of attraction agree with the results of bifurcation diagrams obtained by a continuation method. Next, for α 3 = 0.05 we observe only one double point attractor (no. 1, corresponding to the solution of no. 1 in Fig. 7b) with the pink colour basins of attraction. Introducing MR damping caused a reduction of the pendulum vibration centre shift while the basins of attraction for semi-trivial solution are much larger with a less complicated structure. Because the basins of attraction have a fractal structure, the control of dynamics using the initial condition of the pendulum is very difficult. Therefore, we used the amplitude of the pendulum as the control signal.

In order to control the system in the closed-loop algorithm, Eq. 1 can be modified by substituting α 3 with

$$ \alpha_3=\alpha_3(u(\varphi, \tau)) $$
(5)

where \(u=f(\varphi,\tau)\) is a control function which depends on the time and position of the pendulum. The scheme of closed-loop control algorithm to jump from attractor nos. 2 to 3 or from attractor nos. 3 to 2 is presented in Fig. 9. Based on results in Fig. 7b, in order to control a jump between attractors nos.2 and 3 (case 1) or vice versa (case 2), the following value of MR damping parameter is assumed

$$ \alpha_3(u)=\left\{ \begin{array}{ll} 0.01&{\rm if}\;u \geq 0 \\ 0.05& {\rm if}\;u<0 \end{array} \right. $$
(6)

where u is calculated from a simple function u = τ − U. Parameter U for the system without control, have constant value U = 0 when \(\tau\in\langle{0,1{,}000}\rangle, \) then u ≥ 0 and α 3 = 0.01. For time \(\tau\in(0,\infty)\) the proposed control method is activated. Now, parameter U have initial values U = 0 and is to be reinitialized U = τ i  + 50 in the point i when \(\varphi(\tau_i)>1.1\) (case 1) or \(\varphi(\tau_i)<\,{-}1.1\) (case 2). New value of U gives possibility to change damping to α 3 = 0.05, because u < 0 in time window \(\tau\in\langle{\tau_i,\tau_i+50}\rangle. \) Analyzing the results presented in Figs. 10 and 11, we may conclude that the pendulum swings can be controlled by application of a simple control algorithm based on amplitude of the pendulum response. During the second impulse of the MR damping activation, the pendulum jumps from attractor nos. 2 to 3 (Fig. 11) or 3 to 2 (Fig. 11).

The change of the pendulum solution occurs smoothly and does not cause a temporary increase of oscillator vibrations. Disadvantage of the proposed control method is that we have to know an exact number of solutions for the applied MR damping.

4 Chaotic motion under MR damping influence

4.1 Influence MR damping on chaos

Chaos is a state where small variations in initial conditions produce different results, in such a way that the long-term behaviour of chaotic systems cannot be predicted. This kind of motion is unwanted, if the pendulum is to play the role as a dynamical absorber.

The two parameter space plots are calculated to investigate the effects of the influence of MR damping on chaos near the main resonance. For each value of the varied parameter, the same initial conditions (all equal to zero except \(\varphi=0.1\)) are used. The following parameters identified from laboratory rig [4] are used to simulations: α 1 = 0.3054, α 2 = 0.1, μ = 14.6863, λ = 0.1342, q = 2.3239, γ = 0. The first 500 excitation periods were excluded in the analysis.

In Fig. 12a the two parameter space plot: the frequency of excitation (ϑ) versus MR damping coefficient (α 3) for MR model with hysteretic effect is presented (e 1 = 10, e 2 = 1). A similar plot was calculated for system without a hysteretic loop (Fig. 12b, e 2 = 0) to observe influence of the hysteretic phenomenon on the chaotic behaviour. Both diagrams are similar, but one can see some differences, especially near frequency ϑ = 0.7. The system without a hysteretic loop has a slightly larger chaotic region.

Fig. 12
figure 12

Two parameter space plot: frequency of excitation versus MR damping for system with (a) and without (b) hysteretic loop

Full size image

The blue colour indicates chaotic motions estimated based on value of maximal Lyapunov exponent (Lyap max ). To have better insight into the parameters space plot and its verification, the bifurcation diagrams crosschecks have been done. The vertical cross-check for ϑ = 0.8, Fig. 13a and horizontal cross-check α 3 = 0.35, Fig. 13b are presented. The corresponding maximal Lyapunov exponents and strange attractors (in the chaotic regions) were calculated, too. The positive value of the Lyap max indicates that the blue area in bifurcation diagrams represents the chaotic behaviour. As we may see, the chaotic response occurs near the main parametric resonance (and near the absorption region), located between ϑ ≈ 0.6 − 1.35. We can clearly observe that MR damping generally can reduce chaotic motion.

Fig. 13
figure 13

Bifurcation diagrams and maximal Lyapunov exponents: vertical crosscheck for ϑ = 0.8 (a) and horizontal crosscheck for α 3 = 0.35 (b) of Fig. 12a

Full size image

However, increase MR damping for some parameters can give rise to chaotic motion (for example, the new region near: ϑ ≈ 0.8 α 3 ≈ 0.5, in Fig. 12a). It means that the increase of MR damping may not guarantee suppression of chaotic oscillations. Therefore, the control method should be applied.

4.2 Chaos and rotation control

As it is pointed in papers [4, 22] and as well in the previous paragraph, the autoparametric system can exhibit dangerous motion near the main parametric resonance. If a system works in this region then, rotation or chaotic oscillations occur. Therefore, we present a qualitative analysis of the pendulum motions, based on the pendulum velocity and magnetorheological damping. The calculations were performed in Matlab for fixed initial conditions: \(X(0)=0, \dot{X}(0)=0, \varphi(0)=0. \)

Analysing results presented in Fig. 14, possible vibrations of the pendulum are divided in five types:

Fig. 14
figure 14

Types of pendulum motions versus MR damping: orange—the pendulum is in upper or lower position (semi-trivial solution), yellow—rotation, blue—an asymmetric vibrations, navy blue—symmetric vibrations, brown—chaotic motion, frequency ϑ = 0.8. (Color figure online)

Full size image
  1. 1.

    Chaotic motion (brown colour) This kind of vibrations was identified based on the difference between the original trajectory \((\varphi{(\tau)}, \dot\varphi(\tau)), \) and the perturbed trajectory \((\varphi_0(\tau), \dot\varphi_0(\tau)), \) of the pendulum. Calculations of the second trajectory start at time τ * = 5,000. At the moment perturbed trajectory has initial values \(\varphi_0(\tau^*)=\varphi(\tau)+\delta\varphi\) and \(\dot\varphi_0(\tau^*)=\dot\varphi(\tau)+\delta\dot\varphi\) where \(\delta\varphi=\delta\dot{\varphi}=10^{-6}. \) In the calculations it was assumed that system vibrations are chaotic when max\((\sqrt{(\varphi(\tau)-\varphi_0(\tau))^2+(\dot\varphi(\tau)-\dot\varphi_0(\tau))^2})>0.005, \) for \(\tau\in\langle{5000}-7000\rangle. \) If the relationship is not satisfied them pendulum vibrations are regular.

  2. 2.

    Regular motion:

    1. 2a

      (orange colour). The pendulum is located in the upper or lower position when \(\varphi(\tau)=\pi+k2\pi, \) or \(\varphi(\tau)=2k\pi, \) for k = 1, 2, … , respectively. This kind of motion was identified by a simple criterion \(\dot\varphi(\tau)=0, \) in practice abs(\(\dot\varphi(\tau))<\epsilon_1=0.001. \)

    2. 2b

      (yellow colour). The pendulum rotates in clockwise or counter clockwise direction. In this case, velocity of the pendulum satisfies one of the conditions: max\((\dot\varphi(\tau))>0\) and \((\dot\varphi(\tau))>0\) or max\((\dot\varphi(\tau))<0\) and min\((\dot\varphi(\tau))<0. \)

    3. 2c

      (blue colour). An asymmetrical (shifted) swings of the pendulum. The mean of vibrations is shifted from the upper or lower position. In numerical considerations description of this kind of vibrations was accepted by the form: max\((\dot\varphi(\tau)>)0, \) min\((\dot\varphi(\tau))<0\) and abs(mean\((\dot\varphi))>\epsilon_2=0.01. \)

    4. 2d

      (navy blue colour). Symmetrical (classical) vibrations. It is the last kind of motion where mean of value vibrations is kπ for k = 0, 1, 2, …. Now, this motion have to satisfy the relations: max \((\dot\varphi(\tau))>0, \) min\((\dot\varphi(\tau))<0\) and abs(mean\((\dot\varphi))<\epsilon_2=0.01. \) The variant 2a (ST solution) is a special case of variant 2d.

Controlling of the system dynamics by angular velocity of the pendulum is difficult, because MR damping must be activated precisely for the selected pendulum position. Therefore, we propose impulse activation or deactivation of MR damping in closed-loop algorithm until a satisfactory solution is obtained.

In order to control in the closed-loop algorithm, the Eq. 5 can be modified to

$$ \alpha_3=\alpha_3(u(\dot\varphi, \tau)) $$
(7)

where \(u=u(\dot\varphi, \tau)\) is a control function. Figure 14 presents the possibility of the existence of two kinds of motions for α 3 = 0.45. The pendulum can rotate (2b) or perform an asymmetrical vibrations (2c). To change solution from (2c) to (2b) and vice versa following control method is proposed

$$ \alpha_3(\tau)=\left\{ \begin{array}{ll} A & {\rm if} \; \tau-u \geq 0 \\ A_C & {\rm if} \; \tau-u<0 \end{array} \right. $$
(8)

where A is a MR damping for system without control, A C is MR damping used for control. The Eq. 8 can be used to describe two control algorithms. The first method generates a jump from swings to rotation of the pendulum (case from type of motion: 2c to 2b), Fig. 15. The system without control has constant value of control function u(τ) = 0 for \(\tau\in\langle{0,2{,}000}\rangle\) and MR damping is α 3 = A = 0.45.

Fig. 15
figure 15

Time histories of the pendulum (a, b), the oscillator (c) and changes of magnetorheological damping (d) during the jump from solution no. 2c to 2b, for: \(\dot\varphi(\tau=0)=\frac{\pi}{4}, \) A = 0.45, A C  = 0.1, B = 0.01

Full size image

For the system with the control for \(\tau\in(2{,}000,\infty), \) u(τ = 2,000) = 0 and u(τ) can be changed to new value \(u(\tau)=\tau+\Updelta\tau\) when abs\((\dot\varphi(\tau))<B\) and τ − u(τ) > 0. This change of the control function \(u(\tau)=\tau+\Updelta\tau\) causes existence of a time window \(\Updelta\tau \,{\rm when}\,\tau-u(\tau)<0\) and magnetorheological damping is activated to value α 3 = A C . In numerical calculations length of this time window \(\Updelta\tau\) is 50. Values of parameters are A C  = 0.1 and B = 0.01, where B is a parameter estimated from time series. In this case magnetorheological damping α 3 = A C  = 0.1 has smaller values than system without control α 3 = A = 0.45. Second parameter B have to be close to zero, because absolute values of pendulum velocity abs\((\dot\varphi(\tau))\) for rotation is greater than zero. When abs\((\dot\varphi(\tau))\) approaches to zero and is smaller than B, abs\((\dot\varphi(\tau))<B, \) then a change of the damping is activated. A final effect of the first method is a jump of the solution to rotation, Fig. 15.

In the opposite case, the second method changes the solution from rotation to swings of the pendulum. In the presented case a jump from 2b to 2c is possible for parameters A C  = 0.7 and B = 1.1 (Fig. 16). Now magnetorheological damping α 3 = A C  = 0.7 has greater values than system without control α 3 = 0.45. The pendulum has the highest velocity during rotation, therefore parameter B have to be estimated from time series as 0.9 max\((\dot\varphi(\tau)). \)

Fig. 16
figure 16

Time histories of the pendulum (a, b), the oscillator (c) and changes of magnetorheological damping (d) during the jump from solution no. 2b to 2c, for: \(\dot\varphi(\tau=0)=\frac{\pi}{2}, \) A = 0.45, A C  = 0.7, B = 1.1

Full size image

The control function can be changed for the condition abs\((\dot\varphi(\tau))>B\) and τ − u(τ) > 0. This modification can produce a jump from rotation to another attractor.

Considered control methods were tested and the results are shown in Fig. 16.

Analysing results presented in Figs. 15 and 16, we can conclude that selection of the solution is possible by application of the proposed control algorithm.The same control methods were used to change solution from motion denoted as 1 (chaotic motion) to 2b (rotation) and vice versa (see Fig. 17).

Fig. 17
figure 17

Time histories of the pendulum (a, b), the oscillator (c) and changes of magnetorheological damping (d) during the jump solution from no. 1 to 2b, for: \(\dot\varphi(\tau=0)=\frac{\pi}{4}, \) A = 0.35, A C  = 0.1, B = 0.01

Full size image

The proposed control allows a quick change from one kind of motion into other. Additionally, the presented algorithms can be easily applied to a experimental system (which is already built and now algorithms are implemented). Experimental investigations are important, because of possible practical applications, e.g. to maintain the rotation of the pendulum (harvester problem) or to suppress the oscillator motion by the pendulum swinging (the pendulum absorber) (see Fig. 18).

Fig. 18
figure 18

Time histories of the pendulum (a, b), the oscillator (c) and changes of magnetorheological damping (d) during the jump solution from no. 2b to 1, for: \(\dot\varphi(\tau=0)=\frac{\pi}{2}, \) A = 0.35, A C  = 0.7, B = 1.1

Full size image

The MR dampers are among the most promising devices for vibration suppression in many fields of engineering interest, both structural and mechanical [23]. Additionally, these devices are semiactive devices which offer the flexibility and versatility of the active systems and the reliability of the passive ones [24]. The advantage of MR dampers over conventional dampers are that they are simple in construction, compromise between high frequency isolation and natural frequency isolation, they of fer semi-active control, use very little power, have very quick response, has few moving parts, have a relax tolerances and direct interfacing with electronics [25].

5 Conclusions and remarks

The dynamic response, bifurcation analysis and closed-loop control of a magnetorheologically damped Duffing system with an attached pendulum vibration absorber, operating under the parametric resonance conditions, are discussed in this paper. The MR damping analysis shows that an increase of the MR oscillator damping practically does not reduce the absorption effect (Fig. 6a shows an almost constant pre-bifurcation value of the maximum amplitude of oscillation versus α 3). This result is essential, because α 3 parameter can be used to control the system without a loss of an efficiency of dynamic vibration suppression.

The MR damping generally reduced chaotic motion, but for some MR damping parameters we are able to raise of chaotic vibrations (change the rotation into chaos). Additionally, by applying MR damping, we can move the chaotic regions.

The numerical study reveals that for selected parameters two different stable solutions are possible. They are characterised by a positive or negative shift of the vibration centre. The direction of the shift depends on the initial conditions put on pendulum motion. The range of parameters for which one or more stable or unstable solutions may exist has been determined by a continuation method.

The activation of MR damping, for a specific position of the pendulum seems to be difficult to be used in practice because of a fractal structure of the basins of attraction. Therefore, methods of control based on the pendulum angular velocity and displacement is proposed. These methods allow keeping the response on the required attractor or change one solution into another in a quick way. The impulse activation does not cause a change the proper tuning of the system.

In the next step the proposed algorithms to control, rotation, swinging or chaotic motion of the pendulum will be implemented in a real laboratory system. Moreover, an especially designed SMA spring will be added to create “smart active suspension”.