A strong formulation finite element method (SFEM) based on RBF and GDQ techniques for the static and dynamic analyses of laminated plates of arbitrary shape

Abstract

This paper deals with the static and dynamic analyses of multi-layered plates with discontinuities. The two-dimensional first-order shear deformation theory is used to derive the fundamental system of equations in terms of generalized displacements. The fundamental set, with its boundary conditions, is solved in its strong form. A new method termed strong formulation finite element method is considered in the present paper to solve this kind of plates. This numerical methodology is the cohesion of derivative evaluation of partial differential systems of equations and a domain sub-division. The numerical results in terms of natural frequencies and maximum deflections are compared to literature and to the same results obtained with a finite element code. The stability, accuracy and reliability of the present methodology is shown through several numerical applications.

1 Introduction

The problem of composite plates [1–13] is one of the most studied problems in mechanical, civil and aerospace engineering, due to its high applicability to several practical applications. It often occurs that the physical geometry under consideration does not have a regular shape, such as a rectangle or circle, but it is arbitrary and in some other cases it presents cracks and discontinuities as well as holes.

The present paper deals with these geometries. Thus, arbitrarily shaped plates with geometric discontinuities are considered. In order to well treat each discontinuity of the model, the whole physical domain is divided into several sub-domains, or elements, according to the problem geometry. Inside each element an higher order numerical scheme is used for solving the equations of the problem in their strong form within their boundary conditions. Furthermore, the connections between the elements have been dealt with continuity conditions among them.

Domain decomposition techniques currently in use are based on spectral methods (SMs) [14–17]. The key components of SMs formulation are the trial functions (also called the expansion or approximating functions) and the test functions (also known as weighting functions). The approximating functions, which are linear combinations of suitable basis functions, are used to provide the approximation of the unknown solution. The weighting functions are used to ensure that the differential equation and its boundary conditions are satisfied as closely as possible by the truncated series expansion (the residual should tend to zero). This is achieved by minimizing, with respect to a suitable norm, the aforementioned residual. For this reason these methods can be seen as particular weighted residual methods. The choice of the basis functions is one of the features which distinguishes SMs from the finite element method (FEM). The basis functions for SMs are infinitely differentiable and global functions, whereas in the h-version of FEM, the domain is divided into small elements, and low-order trial functions are specified in each element. Therefore, these functions have a local character and well suited for handling complex geometries. On the contrary the classical SMs (on a single tensor-product domain) are global, so they are formulated for handling simple geometries, such as squares and rectangles. In some cases, since SMs use global basis functions of high degree over the entire domain, the basis functions can be chosen to satisfy the boundary conditions of a boundary value problem. Hence the boundary conditions do not have to be necessarily satisfied. When a general domain is divided into sub-domains or elements this condition cannot occur due to the fact that the elements are disjoint. It turns out that the easiest way to match spectral expansions across sub-domain walls is to use the variational formalism of finite elements, because they can be a-priori enforced and they convert differential equations into sparse rather than dense matrices which are cheaper to invert [16]. However, for some problems finding the variational form of a differential system can be cumbersome. For this reason the use of strong formulation based elements can be a good alternative, nevertheless these elements need proper boundary conditions among the elements.

In recent years, many researchers developed and extended the SM concepts (known also as collocation [16]) in order to solve any kind of differential problem related to the most common engineering applications. This group of numerical techniques include, for instance, radial basis function (RBF), generalized differential quadrature (GDQ) methods and iso-geometric analysis (IGA). Several papers about RBF [18–38], GDQ [39–82] and IGA [83–87] can be found in literature.

The main difference among these methods is the choice of different approximating polynomials. For instance, RBFs use certain basis functions ϕ whereas GDQ is based on Lagrange interpolating polynomials $\mathcal {L}$. The main advantage of GDQ is that it leads to very accurate results with a small amount of grid points, but it can only be applied on regular grid of collocation points. On the other hand RBFs do not need a regular collocation but their accuracy depend on a shape parameter that must be defined before the analysis in order to have reliable solutions [33, 37].

For treating more general geometries the so-called spectral element methods (SEMs) [16, 88–90] were developed. They can be considered as a mix between SMs and FEMs. A SEM combines the generality of the FEM with the accuracy of spectral techniques. In particular the two approaches are very similar in some cases. The one-element variational finite element approximation (the so-called Raleigh–Ritz procedure) is exactly equivalent to a Galerkin spectral approximation if the basis functions are the same. The global domain decomposition techniques followed the historical path of spectral element approach, using mainly Chebyshev collocation [88–90], unfortunately it is not possible to cite them all, so only the main contributions have been given in this paper. It is pointed out that there are some mesh free applications based on smooth approximation [91–93]. They are the so-called natural element method, that are based on natural neighbor interpolation. Natural neighbor interpolation is a multivariate scattered data interpolation method. These interpolants are constructed on the basis of the underlying Voronoi tessellation which partitions a given set of nodes. The interested reader might refer to the works [91–93] for further reading on the subject.

With the advent of the GDQ method [15] in 1991, new numerical applications have been proposed [40, 42, 94–115]. The present new approach, which follows the main guidelines of SEM, merges the mapping technique, used in FEM [4], with the GDQ method. In this way it is possible to solve complex problems with mechanical and geometric discontinuities. It should be pointed out that a unified framework for a systematic derivation of complex stretchings for all fields and exterior differentiation operators is presented in the work [116]. In particular, the algebraic structure of the construction for arbitrary curvilinear systems of coordinates are exposed and practical rules for transformation of bilinear forms corresponding to classical weak formulations are established.

The present methodology has already been applied using GDQ method in the past [109, 111–115, 117–119], but it has never been presented using RBFs. The connections between the elements are treated with compatibility conditions between adjacent edges according to the theory under consideration. In other words the elements are connected by “patching” because the solution in different elements is matched along their common boundary by requiring that the solution and a finite number of its derivatives are equal along the interface. This means that domain decomposition based on strong form splits the computational region into several smaller regions or “sub-domains”. A separate Chebyshev, Legendre or polynomial expansion is then defined on each sub-domain, and the expansions are matched together at the sub-domain boundaries. On the contrary SEM subdivides the computational domain into several subintervals and then separate spectral series are employed on each interval. It differs from the sub-domain method only by employing a variational principle and integration-by-parts.

In this paper, similarly to what was previously mentioned, the authors implemented a new technique that uses RBF method and mapping technique for solving multi-layered FSDT plates. At first glance merging RBF with mapping technique could be useless because RBF can deal with discontinuities without the domain division. However, when the number of points in the single element increases the coefficient matrix of RBFs tends to be ill-conditioned and does not yield to accurate results. For this reason the idea of dividing the domain into sub-domains and the use of less points for each element reduce the matrix ill-conditioning problem and simplify the initial problem.

Summarizing, the aim of this paper is to study the static and dynamic behavior of multi-layered structures via RBF and GDQ methods when a sub-domain technique is used. For the sake of conciseness this method is termed strong formulation finite element method (SFEM) throughout the paper, because the strong form of the partial differential system of equations is solved at the master element level.

Convergence, reliability and stability of the SFEM is investigated and the numerical results are compared with those found in literature and obtained through a finite element code, in the final section.

2 FSDT for flat plates

The shape of a plate is adequately defined by describing the geometry of its middle surface, that bisects the plate thickness h. Originally the first order shear deformation theory (FSDT) was derived for isotropic plates using equilibrium considerations, however that is not always easy when composite plates are considered. Therefore, the fundamental set of equations is derived starting from the kinematics. In fact a laminated plate is made of l layers, so that the total plate thickness is given by the sum of each layer through the thickness of the plate $h=\sum\nolimits_{k=1}^l h_k,$ where h _k is the thickness of the kth lamina or ply. A description of multi-layered plates can be found in [3], where the fundamental assumptions are drawn. It is also underlined that the FSDT is valid, compared to three-dimensional elasticity solution, until ${1}/{100} \le {h}/{L} \le {1}/{10},$ where L is the shortest dimension of the plate at issue.

As it is well-known the FSDT has five independent degrees of freedom, that lay on the middle surface of the plate. The present theory is called also linear because the in-plane displacements are linear through-the-thickness, whereas the out-of-plane displacement is constant

$$U(x,y,z,t) = u(x,y,t) + z \beta _x(x,y,t)$$

(1)

$$V(x,y,z,t) = v(x,y,t) + z \beta _y(x,y,t)$$

(2)

$$W(x,y,z,t)= w(x,y,t)$$

(3)

x, y are the Cartesian coordinates that defines the undeformed configuration of the middle surface of the plate. z is the vertical (normal) coordinate and t is the time. It is noted that the displacement parameters are u, v, w, β _x , β _y .

From the displacement field (3) using the three dimensional kinematic equations [3], the strain characteristics as functions of the generalized displacement parameters can be found

$$\left[ \begin{array}{l} \varepsilon _x^0 \\ \varepsilon _y^0 \\ \gamma _{xy}^0 \\ \chi _x \\ \chi _y \\ \chi _{xy} \\ \gamma _x \\ \gamma _y \end{array}\right] = \left[ \begin{array}{lllll} \frac{\partial }{\partial x} & 0 & 0 & 0 & 0 \\ 0 & \frac{\partial }{\partial y} & 0 & 0 & 0 \\ \frac{\partial }{\partial y} & \frac{\partial }{\partial x} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{\partial }{\partial x} & 0 \\ 0 & 0 & 0 & 0 & \frac{\partial }{\partial y} \\ 0 & 0 & 0 & \frac{\partial }{\partial y} & \frac{\partial }{\partial x} \\ 0 & 0 & \frac{\partial }{\partial x} & 1 & 0 \\ 0 & 0 & \frac{\partial }{\partial y} & 0 & 1 \\ \end{array}\right] \left[ \begin{array}{l} u \\ v \\ w \\ \beta _x \\ \beta _y \end{array} \right]$$

(4)

where the strain characteristics vector $\varvec{\varepsilon } = \left[ \varepsilon _x^0 \, \varepsilon _y^0 \, \gamma _{xy}^0 \, \chi _x \, \chi _y \, \chi _{xy} \, \gamma _x \, \gamma _y \right]^T$ is related to the displacement parameter vector ${\mathbf {u}} = \left[ u \, v \, w \, \beta _x \, \beta _y \right]^T$ through the kinematic operator that it is indicated by D, so that Eq. (4) becomes $\varvec{\varepsilon }=\mathbf {Du}$.

The relationships between stresses and strains are established through the constitutive equations, where the materials under consideration have linear elastic properties. In order to study moderately thick laminated composite plates, a perfect bonding between layers is considered [3, 67]. The initial three-dimensional problem is turned into a two-dimensional one, and using FSDT assumptions the normal strain ε _n and stress σ _n are negligible, so only eight constitutive equations are needed.

The stress components, integrated through the plate thickness, define the stress resultants that can be directly related to the strain characteristics vector $\varvec{\varepsilon }$.

$$\left[ \begin{array}{l} N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy} \\ T_x \\ T_y \end{array} \right] = \left[ \begin{array}{llllllll} A_{11}^{(0)} & A_{12}^{(0)} & A_{16}^{(0)} & A_{11}^{(1)} & A_{12}^{(1)} & A_{16}^{(1)} & 0 & 0 \\ A_{12}^{(0)} & A_{22}^{(0)} & A_{26}^{(0)} & A_{12}^{(1)} & A_{22}^{(1)} & A_{26}^{(1)} & 0 & 0 \\ A_{16}^{(0)} & A_{26}^{(0)} & A_{66}^{(0)} & A_{16}^{(1)} & A_{26}^{(1)} & A_{66}^{(1)} & 0 & 0 \\ A_{11}^{(1)} & A_{12}^{(1)} & A_{16}^{(1)} & A_{11}^{(2)} & A_{12}^{(2)} & A_{16}^{(2)} & 0 & 0 \\ A_{12}^{(1)} & A_{22}^{(1)} & A_{26}^{(1)} & A_{12}^{(2)} & A_{22}^{(2)} & A_{26}^{(2)} & 0 & 0 \\ A_{16}^{(1)} & A_{26}^{(1)} & A_{66}^{(1)} & A_{16}^{(2)} & A_{26}^{(2)} & A_{66}^{(2)} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & A_{44}^{(0)} & A_{45}^{(0)} \\ 0 & 0 & 0 & 0 & 0 & 0 & A_{45}^{(0)} & A_{55}^{(0)} \\ \end{array} \right] \left[ \begin{array}{l} \varepsilon _x^0 \\ \varepsilon _y^0 \\ \gamma _{xy}^0 \\ \chi _x \\ \chi _y \\ \chi _{xy} \\ \gamma _{x} \\ \gamma _{y} \end{array} \right],$$

(5)

where, ${\mathbf {S}}=\left[ N_x \, N_y \, N_{xy} \, M_x \, M_y \, M_{xy} \, T_x \, T_y \right]^T$ is the stress resultant vector and the stiffness coefficients $A_{ij}^{(\tau )}$ depend on the elastic coefficients $\bar{Q}_{ij}^{(k)}$ and are defined as $A_{ij}^{(\tau )} = \sum _{k=1}^l \int _{\zeta _k}^{\zeta _{k+1}}\bar{Q}_{ij}^{(k)}\zeta ^{\tau } d\zeta$, for $i,j=1,2,6$ and $\tau =0,1,2,\,$ $A_{ij}^{(0)} = \sum _{k=1}^l \int _{\zeta _k}^{\zeta _{k+1}}\kappa \bar{Q}_{ij}^{(k)} d\zeta,$ for $i,j=4,5,$ where the $\bar{Q}_{ij}^{(k)}$ indicates a generic constant for the kth lamina, that are defined in the global reference system [3, 57, 60, 67] and κ is the shear correction factor $\kappa =5/6$ for the case under consideration.

The equilibrium equations of FSDT plates is derived from the Hamilton principle [3, 67]

$$\left[ \begin{array}{llllllll} \frac{\partial }{\partial x} & 0 & \frac{\partial }{\partial y} & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{\partial }{\partial y} & \frac{\partial }{\partial x} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \frac{\partial }{\partial x} & \frac{\partial }{\partial y} \\ 0 & 0 & 0 & \frac{\partial }{\partial x} & 0 & \frac{\partial }{\partial y} & -1 & 0 \\ 0 & 0 & 0 & 0 & \frac{\partial }{\partial y} & \frac{\partial }{\partial x} & 0 & -1 \end{array}\right] \left[ \begin{array}{l} N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy} \\ T_x \\ T_y \end{array} \right] +\left[ \begin{array}{l} q_x \\ q_y \\ q_{z} \\ m_x \\ m_y \end{array} \right] = \left[ \begin{array}{lllll} I^{(0)} & 0 & 0 & I^{(1)} & 0 \\ 0 & I^{(0)} & 0 & 0 & I^{(1)} \\ 0 & 0 & I^{(0)} & 0 & 0 \\ I^{(1)} & 0 & 0 & I^{(2)} & 0 \\ 0 & I^{(1)} & 0 & 0 & I^{(2)} \end{array} \right] \left[ \begin{array}{l} \ddot{u} \\ \ddot{v} \\ \ddot{w} \\ \ddot{\beta }_x \\ \ddot{\beta }_y \end{array} \right]$$

(6)

where the double dot $\ddot{}=\frac{\partial ^2}{\partial t^2}$ indicates the second order derivative with respect to time and the external load vector is indicated by ${\mathbf {q}}=\left[ q_x \, q_y \, q_{z} \, m_x \, m_y \right]^T$. In compact matrix form equation (6) can be written as ${\mathbf{D}^{*}{\mathbf{S}}}+{\bf q}={\bf M}{\ddot{\bf{u}}}$, where $\mathbf {D^*}$ is the equilibrium operator and M is the inertia matrix, also called mass matrix. The inertias are indicated by $I^{(0)}$, $I^{(1)}$ and $I^{(2)}$ and they can be computed as $I^{(\tau )} = \sum _{k=1}^l \int _{\zeta _k}^{\zeta _{k+1}} \rho ^{(k)}\zeta ^\tau d\zeta$, for $\tau =0,1,2$, where $\rho ^{(k)}$ is the density of the kth ply.

The equations of motion (6) can be expressed in terms of the displacement parameters vector u, using Eqs. (4) and (5) to relate the force and moment resultants to the displacement parameters.

In order to solve the dynamic problem, the boundary conditions must be enforced. Since the considered plates are of arbitrary shape, external boundary conditions depend on the outward normal direction of each boundary. Moreover, the connectivity conditions between couples of adjoining elements have to be enforced in a sub-domain application. It should be noted that for a classic GDQ implementation only external conditions are imposed [39, 41–45, 47–50, 56, 58, 60, 61, 64–66, 72–74, 79]. Regarding the continuity conditions between two adjacent edges, a kinematic and a static equation are imposed. The implementation of these kind of conditions are well developed in the works [97, 102–105, 108, 109, 111, 112] where they were proposed for the GDQFEM. However since RBF and GDQ methods are both based on the strong formulation of the differential problem, they follow the same implementation. As a result using the equation of transformation from a Cartesian system x−y to the local reference system at the generic edge n−s (where n is the normal component and s is the tangential component to the edge) the stress resultant vector ${\mathbf {S_n}} = \left[ N_n \, N_{ns} \, T_n \, M_n \, M_{ns} \right] ^T$ acting on a generic side is related to the Cartesian stress resultant vector S by the direction cosines of the outward unit normal vector n

$$\left[ \begin{matrix} N_n \\ N_{ns} \\ T_n \\ M_n \\ M_{ns}\end{matrix} \right] = \left[ \begin{array}{cccccccc} n_x^2 & n_y^2 & 2n_xn_y & 0 & 0 & 0 & 0 & 0 \\ -n_xn_y & n_xn_y & n_x^2-n_y^2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & n_x & n_y \\ 0 & 0 & 0 & n_x^2 & n_y^2 & 2n_xn_y & 0 & 0 \\ 0 & 0 & 0 & -n_xn_y & n_xn_y & n_x^2-n_y^2 & 0 & 0 \end{array} \right] \left[ \begin{matrix} N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy} \\ T_x \\ T_y \end{matrix} \right],$$

(7)

where the matrix N is called transformation matrix and it lets to indicate equation (7) as $\mathbf {S_n=NS}.$ It is pointed out that when inter-element compatibility conditions are considered, the third line of expression (7) has to be replaced by $T_n = T_x\left( n_x-n_y\right) ^2 + T_y\left( n_x+n_y\right) ^2.$

3 Strong formulation finite element method

In the present paper a sub-domain technique using RBF and GDQ methods for the solution of a partial differential system of equations is carried out. Therefore, the authors want to study the static and dynamic behavior of a plate element in which the RBFs and Lagrange polynomials are used for the solution of the equations of motion.

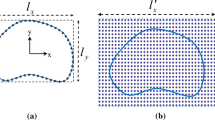
It is obvious that most of the practical engineering problems are not solvable using simple geometries, such as the one depicted in Fig. 1a). For instance, they can present holes, curved boundaries, different boundary and loading conditions as well as different mechanical properties. As a result in order to solve a given problem, the physical domain has to be divided into sub-domains according to the problem geometry, as shown in Fig. 1b) where the domain at issue is divided into eight sub-domains with eight node elements. These sub-domains can be called elements according to the analogy with the finite element technique, that considers an analogous division in order to solve a problem. If the physical problem (represented by Fig. 1a)) has a regular shape, for example that can be divided in rectangles, the methodology is better known as multi-domain technique because it assemblies regular sub-domains (squares or rectangles) [15, 40, 106, 109]. On the other hand if irregular elements are considered, mapping technique must be introduced. As it can be seen from Figure 1b), the resulting elements do not have a regular shape. Hence, a mapping technique has to be introduced in order to transform an element described in Cartesian coordinates x−y, into a master element that is regular (square) and belongs to a computational domain ξ−η. Summarizing the three main steps of any numerical methodology [3], that have the scope to divide the whole domain into sub-domains, are

• 1. Physical problem that can have any kind of complexity

• 2. Domain division or discretization process which leads to a global mesh

• 3. Mapping technique that map an equation set from Cartesian coordinates to a computational domain

Fig. 1

General engineering problem: a physical problem geometry, b discretization for numerical simulation

From the latter step onwards the domain equations have to be solved inside each element in the computational region. The major problem in a multi-domain technique is the treatment of the interfaces among the elements that can greatly reduce accuracy and convergence rate. However element connectivity and boundary conditions have to be enforced in order to solve the global system of equations as graphically shown in Fig. 2a). The generic element $\Omega ^{(n)}$ (for $n=1,2,\dots ,n_e,$ where $n_e$ is the total number of elements) has external and inter-element boundary conditions, nevertheless this aspect will be exposed later in this section.

Fig. 2

a General sketch of a domain decomposition and b a single element computational scheme

3.1 Mapping technique

As far as the mapping procedure is concerned, it is well-known that the Cartesian vector x can be mapped according to a local system ξ as

$$\mathbf {x} = \mathbf {x}(\varvec{\xi }),\quad \text { for }\quad{\mathbf {x}}=\left[ x \quad y \right] ^T, \quad {\varvec{\xi }}=\left[ \xi \quad \eta \right] ^T$$

(8)

The mapping function has to be continuous, differentiable and invertible.

Since the equations for thick composite plates are solved in their strong-form, the second and first order derivatives have to be mapped into the computational system within all the degrees of freedom of the model.

The first order derivative in the Cartesian coordinate system can be found using the chain rule of differentiation

$$\frac{\partial }{{\partial {\bf x}}} = {{\bf J}^{ - 1}}\frac{\partial }{{\partial \upxi }},\quad {\rm{for}}\quad {{\bf J}^{ - 1}}\left[ {\begin{array}{cc} {{\xi _x}}&{{\eta _x}}\\ {{\xi _y}}&{{\eta _y}} \end{array}} \right],$$

(9)

where ${{\bf J}^{ - 1}}$ is the inverse of the Jacobian matrix of the transformation that is the matrix of the first order derivatives of the computational coordinates $\varvec{\xi }$ with respect to the Cartesian coordinates x. Moreover, for the sake of completeness the meaning of the symbols $\xi _x={\partial \xi }/{\partial x}$, $\eta _x={\partial \eta }/{\partial x}$, $\xi _y={\partial \xi }/{\partial y}$, $\eta _y={\partial \eta }/{\partial y}$ are given.

The second order derivatives are carried out from Eq. (9) and assume the aspect

$$\varvec{\partial }^2_{\mathbf {x}} = \varvec{\Xi }_{\mathbf {x}}^{(2)} \varvec{\partial }^2_{\mathbf {\upxi }}$$

(10)

where $\varvec{\partial }^2_{\mathbf {x}}= \left[ \begin{array}{lll} \frac{\partial ^2}{\partial x^2}&\frac{\partial ^2}{\partial y^2}&\frac{\partial ^2}{\partial x\partial y} \end{array} \right] ^T$ is the vector of the Cartesian second order derivatives, $\varvec{\partial }^2_{\mathbf {\upxi }} = \left[ \begin{array}{lllll} \frac{\partial }{\partial \xi }&\frac{\partial }{\partial \eta }&\frac{\partial ^2}{\partial \xi ^2}&\frac{\partial ^2}{\partial \eta ^2}&\frac{\partial ^2}{\partial \xi \partial \eta } \end{array} \right] ^T$ is the vector of the computational first and second order derivatives and $\varvec{\Xi }_{\mathbf {x}}^{(2)}$ is the following differential operator

$$\varvec{\Xi }_{\mathbf {x}}^{(2)} = \left[ \begin{array}{lllll} \xi _{xx} & \eta _{xx} & \xi _{x}^2 & \eta _{x}^2 & 2\xi _{x}\eta _{x} \\ \xi _{yy} & \eta _{yy} & \xi _{y}^2 & \eta _{y}^2 & 2\xi _{y}\eta _{y} \\ \xi _{xy} & \eta _{xy} & \xi _{x}\xi _{y} & \eta _{x}\eta _{y} & \xi _{x}\eta _{y} + \xi _{y}\eta _{x} \end{array} \right] $$

(11)

The Jacobian matrix J can be obtained starting from Eq. (9) applying the transformation rule (8), as

$${\mathbf {J}} = \left[ \begin{array}{ll} {x}_{\xi } & {y}_{\xi }\\ {x}_{\eta } & {y}_{\eta } \\ \end{array} \right]$$

(12)

By inverting the matrix J obtained above, one can get

$${{\bf J}^{-1}} = \frac{1}{{\det {\bf J}}}\left[ {\begin{array}{cc} {{y_\eta }}&{ - {y_\xi }}\\ { - {x_\eta }}&{{x_\xi }} \end{array}} \right],\quad \det {\bf J} = {x_\xi }{y_\eta } - {x_\eta }{y_\xi },$$

(13)

where $\det \mathbf {J}$ is the determinant of the Jacobian matrix J, which must be non-zero at every point in the master element.

Comparing the two inverse matrices in Eqs. (13) and (9), the following relationships are obtained

$$\xi _x = \frac{y_{\eta }}{\det \mathbf {J}}, \qquad \xi _y = -\frac{x_{\eta }}{\det \mathbf {J}}, \qquad \eta _x = -\frac{y_{\xi }}{\det \mathbf {J}}, \qquad \eta _y = \frac{x_{\xi }}{\det \mathbf {J}}$$

(14)

The substitution of Eq. (14) into Eq. (9) yields

$$\frac{\partial }{{\partial {\bf x}}} = \frac{1}{{\det {\bf J}}}\left[ {\begin{array}{cc} {{y_\eta }}&{ - {y_\xi }}\\ { - {x_\eta }}&{{x_\xi }} \end{array}} \right]\frac{\partial }{{\partial \varvec{\upxi} }}.$$

(15)

Proceeding to the second order derivatives of $\xi$ and η with respect to x and y, they can be expressed as

$$\frac{\partial^2{\xi}}{\partial{x^2}} = \frac{1}{\det {\mathbf{J}}^2}\left({y_{\eta}}{y_{\xi \eta }} - \frac{y_{\eta}^2}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right)_{\xi } - {y_{\xi}}{y_{\eta \eta }} + \frac{y_{\xi }y_{\eta }}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right) _{\eta } \right) \frac{\partial ^2\xi }{\partial y^2} = \frac{1}{\det {\mathbf{J}}^2}\left( x_{\eta }x_{\xi \eta } - \frac{x_{\eta }^2}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right) _{\xi } - x_{\xi }x_{\eta \eta } + \frac{x_{\xi }x_{\eta }}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right) _{\eta } \right) \frac{\partial ^2\eta }{\partial x^2} = \frac{1}{\det {\mathbf{J}}^2}\left( -y_{\eta }y_{\xi \xi } + \frac{y_{\eta }y_{\xi }}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right) _{\xi } + y_{\xi }y_{\xi \eta } - \frac{y_{\xi }^2}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right) _{\eta } \right) \frac{\partial ^2\eta }{\partial y^2} = \frac{1}{\det {\mathbf{J}}^2}\left( -x_{\eta }x_{\xi \xi } + \frac{x_{\eta }x_{\xi }}{\det {\mathbf{J}}}\left( \det {\mathbf{J}}\right) _{\xi } + x_{\xi }x_{\xi \eta } - \frac{x_{\xi }^2}{\det {\mathbf{J}}}\left(\det {\mathbf{J}}\right) _{\eta } \right) $$

(16)

where $\left( \det \mathbf {J}\right) _{\xi }$ and $\left( \det \mathbf {J}\right) _{\eta }$ are the first order derivatives of the determinant of the Jacobian with respect to $\xi$ and η, respectively. Differentiation of $\det \mathbf {J}$ in Eq. (13) leads to

$$\begin{aligned} \left( \det \mathbf {J}\right) _{\xi }&= x_{\xi }y_{\xi \eta } - y_{\xi }x_{\xi \eta } + y_{\eta }x_{\xi \xi } - x_{\eta }y_{\xi \xi } \nonumber \\ \left( \det \mathbf {J}\right) _{\eta }&= -x_{\eta }y_{\xi \eta } + y_{\eta }x_{\xi \eta } - y_{\xi }x_{\eta \eta } + x_{\xi }y_{\eta \eta } \end{aligned}$$

(17)

Finally, the mixed derivatives of $\xi$ and η with respect to x and y are given by

$$\begin{aligned} \frac{\partial ^2\xi }{\partial x\partial y}&= \frac{1}{\det \mathbf {J}^2} \left( -y_{\eta }x_{\xi \eta } + \frac{y_{\eta }x_{\eta }}{\det \mathbf {J}}\left( \det \mathbf {J}\right) _{\xi } + y_{\xi }x_{\eta \eta } - \frac{y_{\xi }x_{\eta }}{\det \mathbf {J}}\left( \det \mathbf {J}\right) _{\eta } \right) \nonumber \\ \frac{\partial ^2\eta }{\partial x\partial y}&= \frac{1}{\det \mathbf {J}^2} \left( -y_{\xi }x_{\xi \eta } - \frac{y_{\eta }x_{\xi }}{\det \mathbf {J}}\left( \det \mathbf {J}\right) _{\xi } + y_{\eta }x_{\xi \xi } + \frac{y_{\xi }x_{\xi }}{\det \mathbf {J}}\left( \det \mathbf {J}\right) _{\eta } \right) \end{aligned}$$

(18)

The coordinate transformation (8) can be applied to any kind of element. In fact, no hypotheses were made in the element definition about the element nodes.

In the present paper 8 node elements are used in all the numerical applications as in the work [112]. The interested reader can find other applications of mapping transformation applied to other strong formulations in literature [39, 94–100, 104–106, 108] and the mathematical developments for a 8 node element can be seen in [109, 111, 112].

It should be noted that the nodes that are needed for the mapping technique (e.g. eight node elements) do not coincide with the grid points inside each element represented in Fig. 2a) for the generic physical domain and in Fig. 2b) for the single SFEM element.

In conclusion at the master element level the derivative discretization has to be performed in order to algebraically solve the partial differential system of equations.

3.2 Differentiation procedure using RBFs and differential quadrature methods

Differently from the well-known FEM [4], where the system of equations is solved in its weak form, in this paper the numerical solution at the master element level is in the so-called strong form, which was presented in the previous section.

A numerical procedure for the calculation of nth order derivatives of a function f(x) is illustrated below. A general basis function $\psi _j(x)$, which can be represented, for example, by RBFs $\phi (r_j(x))$ or Lagrange polynomials $\mathcal {L}_j(x)$ is considered in the following. According to the Weierstrass first theorem, about polynomial approximation of a real valued function f(x) which is continuous in a closed interval, the function can be approximated by a polynomial degree less than N, as

$$f(x) \approx P_N(x) = \sum _{j=1}^N \psi _j(x)\lambda _j $$

(19)

where the quantities $\lambda _j$ are constants. Furthermore $P_N(x)$ constitutes an N-dimensional linear vector space V _N with respect to the operation of the vector and scalar multiplication [15, 41]. In the linear vector space V _N a set of vectors $\psi _j(x)$ is linearly independent. Let x ₁, x ₂, $\dots$, $x_N$ be N points interior to the given domain, that are termed collocation points. The discrete functional values f(x _i ) are calculated in these points as

$$f(x_i) = \sum _{j=1}^N \lambda _j\psi _j(x_i), \text { for }\,i=1,2,\dots ,N $$

(20)

where $\psi _j(x_i)$ are the evaluation of the basis functions in all the points N. It is pointed out that the results of collocation depend on both the points x _i and the functions $\psi _j(x)$. When the constants λ _j are determined, a unique solution is obtained. It is possible to write Eq. (20) in matrix form as

$$\mathbf {f} = \mathbf {A}{\varvec{\lambda }} $$

(21)

where $A_{ij}=\psi _j(x_i)$ are the components of the matrix A, that represents the values assumed by the basis functions in all the points of the domain. ${\mathbf {f}}=[ f(x_1)\,f(x_2)\ldots f(x_N) ] ^T$ is the vector of the function values and ${\varvec{\lambda }}=[ \lambda _1,\,\lambda _2,\ldots,\lambda _N ] ^T$ is the parameter vector in all the points N of the target domain.

Since λ _j does not depend on x _i , by differentiating Eq. (20) of a generic order n, for linearity reasons, the derivative is applied to the basis function $\psi _j(x)$ only

$$ \frac{d^n f}{dx^n}\bigg |_{x_i} = \sum _{j=1}^N \lambda _j \frac{d^n \psi _j(x_i)}{dx^n} ,\quad \text { for }\quad i=1,2,\dots , N $$

(22)

Equation (22) can be rewritten in matrix form as

$${\mathbf {f}}^{(n)}={\mathbf {A}}^{(n)}{\varvec{\lambda }}$$

(23)

Hence, solving the equation (21) the coefficients vector ${\varvec{\lambda }}$ can be evaluated as

$${\varvec{\lambda }} = {\mathbf {A}}^{-1}{\mathbf {f}}$$

(24)

and its result can be substituted into Eq. (23), leading to

$${\mathbf {f}}^{(n)} = {\mathbf {A}}^{(n)}{\mathbf {A}}^{-1}{\mathbf {f}}$$

(25)

It should be noted that the expression (25) allows to find a nth order derivative of a function using the functional values f(x _i ). The equation (25) can be rewritten by introducing the differentiation matrix ${\mathbf {D}}^{(n)}$ as follows

$${\mathbf {f}}^{(n)} = {\mathbf {D}}^{(n)}{\mathbf {f}}$$

(26)

where ${\mathbf {D}}^{(n)}={\mathbf {A}}^{(n)}{\mathbf {A}}^{-1}$. In conclusion the differentiation matrix is given by the product of two matrices: the first one ${\mathbf {A}}^{(n)}$ is the matrix of the nth order derivative of the basis function values in all the grid points, the second one ${\mathbf {A}}^{-1}$ is the inverse matrix of the basis function matrix $\mathbf {A}.$ The expression (20) shows a univariate example, however, the same type of problem can be generalized to the multi-variate case, such as two or three dimensional case.

Considering RBFs $\phi (r_j(x))$ as basis functions of the linear vector space V _N , it states that $\psi _j(x)=\phi (r_j(x),b,c).$ Generally RBFs are functions of the Euclidean distance

$$r_j(x) = \Vert x-x_j \Vert = \sqrt{\left( x-x_j\right) ^2 + c},\quad \text { for }\quad c > 0$$

(27)

and a free parameter b termed shape parameter. In this paper the parameter c = 10⁻⁶ is taken constant in all the computations. It is clear to the reader that the functional derivative presented in Eq. (25) concerns a one dimensional problem, while in the present paper a two dimensional first order plate theory is considered. In this work the distance $r_j(x)$ is computed along the main coordinate lines of the computational element $\xi$-η. Thus, $r_p(\xi )= \Vert \xi - \xi _p \Vert$ for $p=1,2,\dots ,N$ and $r_q(\eta )= \Vert \eta - \eta _q \Vert$ for $q=1,2,\dots ,M$. In other words the distances $r_p(\xi )$, $r_q(\eta )$ are evaluated along two orthogonal lines.

On the other hand, when Lagrange polynomials $\mathcal {L}_j(x)$ are used as basis functions the equation (25) has a different form. Mathematically speaking the Lagrange polynomials can be written as

$$\begin{aligned} \mathcal {L}_j(x) = \frac{{\mathcal {M}}(x)}{{\mathcal {M}}^{(1)}(x_j)\left( x-x_j \right) } \end{aligned}$$

(28)

where

$$\begin{aligned} \mathcal {M}(x)&= \left( x-x_1 \right) \left( x-x_2 \right) \dots \left( x-x_N \right),\\ \mathcal {M}^{(1)}(x_j)&= \prod _{k=1,k\ne j}^N \left( x_j-x_k \right) \end{aligned}$$

(29)

It can be seen that Lagrange polynomials $\mathcal {L}_j(x)$ possess the following property

$$ \mathcal {L}_j(x_i) = \left\{ \begin{array}{ll} 1, &\text { when}\;j = i,\\ 0, &\text { otherwise} \end{array} \right. $$

(30)

Hence, these basis functions have a unitary value at the point x _i and a null value in all the other points. For this reason the matrix of the Lagrange polynomial values is an identity matrix $\mathbf {A}=\mathbf {I}$, so its inverse ${\mathbf {A}}^{-1}$ is trivial.

In conclusion, a polynomial approximation method based on Lagrange interpolation polynomials $\mathcal {L}_j(x)$ (termed GDQ) does not need to calculate the inverse of a matrix (${\mathbf {A}}^{-1}$) in order to evaluate a nth order derivative of a function f(x). This aspect can eliminate many ill-conditioned problems related to some other methods which use basis functions that are not Lagrangian, such as RBFs. In fact it will be shown in the numerical benchmarks that the coefficient matrix A of a few RBFs is highly ill-conditioned and its inversion becomes very difficult when N is large.

As far as the implementation procedure is concerned, the partial derivatives of the flat plate equations can be discretized according to equation (26). In order to improve the knowledge regarding the study of shell structures using GDQ method, the reader should refer to the works [45, 47, 50]. It should be noted that due to the generality of expression (26), which depends on the basis functions chosen, any higher-order computational scheme can be used such as RBF and GDQ methods. In other words the partial differential system of equations, inside a generic element, is written in algebraic form according to equation (26). The calculation of the differentiation matrix components $D_{ij}^{(n)}$ depends on the type of basis functions chosen for the approximation: $D_{ij}^{(n)}=\left( {\mathbf {A}}^{(n)}{\mathbf {A}}^{-1}\right) _{ij}$ if RBFs $\phi (r_j(x),b,c)$ are considered and $D_{ij}^{(n)}=\varsigma _{ij}^{(n)}$ if Lagrange polynomials $\mathcal {L}_j(x)$ are used, where $\varsigma _{ij}^{(n)}$ are the so-called weighting coefficients according to GDQ method [41, 45, 47, 50].

3.3 Boundary conditions implementation

As stated in the introduction the present paper shows the implementation of RBF and GDQ methods using a sub-domain technique. Since it has been demonstrated that RBF method and GDQ method are both SMs and their only difference is the definition of the differentiation matrix (26), the same implementation can be followed using both techniques. The authors already presented a work about GDQFEM recently [112], in which the boundary conditions implementation has been treated in detail. For the sake of conciseness, in the present section, only the main points of the boundary conditions implementation is reported.

In the previous subsection the derivative calculations inside each element have been introduced. As shown in Fig. 2b) each element is composed of three sets of points: domain points, where the equations of motion are discretized (as explained in the previous subsection), the boundary points and the corner points. Thus, each boundary point lays on an edge or at a corner and different boundary conditions have to be enforced according to the problem at issue.

The six element mesh in Fig. 3 is considered, where inter-element edges and external boundaries are indicated with solid blue and black lines respectively. On the other hand Fig. 4 shows the outward unit normal vectors nomenclature for the mesh under consideration. Two groups of points occur: the points on the edges (edge types E) and the ones on the corners (corner types C). If the domain is clamped on some part of its external boundary the Dirichlet type conditions (E1), known also as kinematic boundary conditions, have to be enforced as shown in Fig. 3 on the element $\Omega ^{(1)}$. These conditions are functions of the displacement parameters of the physical model, that are u, v, w, β _x and β _y . On the contrary the Neumann edge type (E2), also known as static boundary condition, is related to the external natural boundary conditions presented in equation (7). It is obvious that expressions (7) are functions not only of the derivative of the displacement parameters (stress resultants) but also of the outward unit normal vector n of the current boundary, in which the natural condition has to be enforced. In general a boundary type E2, referring to the edge 3 of element $\Omega ^{(1)}$ is indicated by ${\mathbf {S}}^{(1)}_{{\mathbf {n}}_{\underline{3}}}$, where S stands for the stress resultant vector. The subscript of the normal vector n indicates the edge, e.g. 3, and the superscript stands for the element in which the normal belong to, e.g. (1). As far as the corner conditions are concerned, it is underlined that the two corner nodes on the edge $\underline{4}$ of $\Omega _1$ are embedded into the Dirichlet condition (E1), because the clamped boundary type is stronger, from the physical point of view, with respect to a natural boundary type condition, whereas the other corners indicated by C1 are different from the Neumann type conditions due to the coexistence of two natural conditions in a single point. As far as single corner type condition (C1) is concerned, the sum of the two stress resultant vectors of the two adjacent edges is imposed. A full treatment of this kind of boundary condition can be found in some GDQ applications for single [72] and multi-domain approach [112]. According to Fig. 4 at corner 1 of element $\Omega ^{(2)}$ the two normals ${\mathbf {n}}^{(2)}_{\underline{4}}$ and ${\mathbf {n}}^{(2)}_{\underline{1}}$ concur at the same corner. Since both edges 4 and 1 need natural boundary conditions to be imposed the stress resultant ${\mathbf {S}}^{(2)}_{{\mathbf {n}}_{\underline{4}}}={\mathbf {0}}$ on the edge 4 and ${\mathbf {S}}^{(2)}_{{\mathbf {n}}_{\underline{1}}}={\mathbf {0}}$ on the side $\underline{1}$. The unique condition that enforce both relationships is

$$ {\mathbf {S}}^{(2)}_{{\mathbf {n}}_{\underline{4}}}+{\mathbf {S}}^{(2)}_{{\mathbf {n}}_{\underline{1}}}={\mathbf {0}}$$

(31)

Fig. 3

Internal and external boundary conditions for element edges and corners

Fig. 4

Outward unit normal vectors definition for a generic sub-division

Consider the so-called compatibility edge type conditions (E3) from Fig. 3. These are the fundamental conditions which connect two facing elements, connected by inter-element edges. In fact in this procedure no overlapping technique [40, 109] has been implemented and the boundary points on the edges are superimposed. In other words, for instance, the grid points of edge 1 of element $\Omega ^{(1)}$ are superimposed to the points of edge 3 of element $\Omega ^{(2)}$. In this way only a group of points can be physically seen, nevertheless a double number of them are computationally considered. This double set of points is needed for the continuity or compatibility conditions implementation. The aforementioned compatibility conditions between two adjacent elements have a dominant influence on the numerical solution. Let the edge 1 of $\Omega ^{(1)}$ and 3 of $\Omega ^{(2)}$ be the two facing edges where the compatibility conditions have to be enforced (see Fig. 4). Mathematically speaking the continuity conditions, at each node of two, on the linear interfaces are

$$\begin{aligned}&u^{(1)} = u^{(4)}, \,\, v^{(1)} = v^{(4)},\,\, w^{(1)} = w^{(4)}, \,\, \beta _x^{(1)} = \beta _x^{(4)}, \,\,\beta _y^{(1)} = \beta _y^{(4)}\nonumber \\&N_{n({\mathbf{n}}_{\underline{1}})}^{(1)} = N_{n({\mathbf{n}}_{\underline{3}})}^{(4)}, \, N_{ns({\mathbf{n}}_{\underline{1}})}^{(1)} = N_{ns({\mathbf{n}}_{\underline{3}})}^{(4)}, \, T_{n({\mathbf{n}}_{\underline{1}})}^{(1)} = T_{n({\mathbf{n}}_{\underline{3}})}^{(4)}, \, M_{n({\mathbf{n}}_{\underline{1}})}^{(1)} = M_{n({\mathbf{n}}_{\underline{3}})}^{(4)}, \, M_{ns({\mathbf{n}}_{\underline{1}})}^{(1)} = M_{ns({\mathbf{n}}_{\underline{3}})}^{(4)} \end{aligned}$$

(32)

In short equation (32) can be written in matrix form as

$$\begin{aligned} {\mathbf {u}}^{(1)}&= {\mathbf {u}}^{(2)} \,{\rm Kinematic\;Conditions}\; \\{\mathbf {S}}^{(1)}_{{\mathbf{n}}_{\underline{1}}}&= {\mathbf {S}}^{(2)}_{{\mathbf{n}}_{\underline{3}}} \,\text { Static\;Conditions}\end{aligned}$$

(33)

Since two sets of points are located at each inter-element edge, two are the sets of continuity conditions that have to be considered. In conclusion the kinematic conditions are imposed on the points of one edge, for example 1 of $\Omega ^{(1)}$, and the static conditions are enforced on the points of the other edge, for instance 3 of $\Omega ^{(2)}$. For the sake of completeness the outward unit normal vector components are reported in the following. Mathematically speaking these components are the direction cosines of the vector n respect to the external Cartesian reference system. A complete treatise of the implementation of these vectors can be found in [109, 111, 112], nevertheless their expressions are reported below for the four sides of a quadrilateral element

$$\begin{aligned}&{\left\{ \begin{array}{l} {n_x} = {\xi} \, {y_{\eta}} \left(x_{\eta }^2 + y_{\eta }^2\right)^{-\frac{1}{2}} \\ n_y = -\xi \, {x_{\eta}}\left(x_{\eta }^2 + y_{\eta }^2 \right)^{-\frac{1}{2}}\end{array} \right. \quad {\text{for}} \quad \xi = \pm 1} \\ &{\left\{ \begin{array}{l} {n_x} = -\eta \, {y_{\xi}} \left(x_{\xi}^2 + y_{\xi }^2\right)^{-\frac{1}{2}} \\ n_y = \eta x_{\xi}\left(x_{\xi}^2 + y_{\xi }^2 \right)^{-\frac{1}{2}}\end{array} \right. \quad {\text{for}} \quad \eta = \pm 1 } \\ \end{aligned}$$

(34)

The relationships (34) are valid for the edges parallel to $\xi$ axis and η axis, respectively. When $\xi$ and η correspond to x and y, the domain gets all the edges parallel to the Cartesian reference system and the technique degenerate in that so-called multi-domain technique.

In conclusion the external and internal corner type conditions (C2) and (C3) have to be described. These types of boundaries have been already presented in the previous works [111, 112]. In the following only a general description of these conditions is given. Since the corner points are superimposed, as well as the points on the edges, the number of conditions that have to be imposed for each corner depend on the number of elements which concur at that node. For example the two corners with (C2) conditions belongs to two neighbour elements. In both case the (C2) condition has the same form as the (E3) one, because only two elements concur at a corner. On the contrary in the internal corner condition (C3) three conditions must be enforced. However the continuity conditions (33) are made of two sets only. The solution to this problem is to impose two kinematic conditions and a static one. For the present case, depicted in Fig. 3, the kinematic conditions are written between $\Omega ^{(4)}$ and $\Omega ^{(6)}$ elements and between $\Omega ^{(6)}$ and $\Omega ^{(5)}$ elements. Whereas the static condition is enforced between $\Omega ^{(5)}$ and $\Omega ^{(4)}$. Since the displacements of the three elements at the correspondent corner are set equal, it implies that writing the equality of the stresses as last condition, it is verified also for the missing elements. Mathematically speaking the (C3) condition can be written

$$\begin{aligned}&\left\{ \begin{array}{l} {\mathbf {u}}^{(4)} = {\mathbf {u}}^{(6)} \\ {\mathbf {u}}^{(6)} = {\mathbf {u}}^{(5)} \end{array}\right. \, \Rightarrow \, {\mathbf {u}}^{(5)} = {\mathbf {u}}^{(4)}\; \text { First\,three\,corner\,conditions} \nonumber \\&{\mathbf {S}}^{(5)}_{{\mathbf {n}}_{\underline{3}}} = {\mathbf {S}}^{(4)}_{{\mathbf {n}}_{\underline{4}}}\; \text { This\,is\,one\,of\,the\,conditions\,that\,can\,be\,chosen} \end{aligned}$$

(35)

Following equations (35) the $\mathcal {C}^1$ continuity conditions among the elements of a given mesh is satisfied. In other words a continuous and smooth stress distribution is guaranteed by expressions (35).

3.4 Assembly procedure

As any numerical approach, in order to find an algebraic solution, the physical domain has to be discretized. From SFEM, a grid distribution is chosen in order to locate the points inside each element. The complete domain mesh and element discretization can be seen in Fig. 2a) in which a general sketch is presented. The numerical approach, for both RBF and GDQ methods, is applied at the master element level in the computational domain $\xi$−η. In the present paper the point distribution is defined by a Chebyshev-Gauss-Lobatto (C-G-L) grid along both $\xi$ and η directions. The grid points coordinates $\bar{\xi }_p$ and $\bar{\eta }_q$ are defined by

$$\begin{aligned} \bar{\xi }_p&=-\cos \left( \frac{p-1}{N-1}\pi \right) , \quad p=1,2,\dots , N\nonumber \\ \bar{\eta }_q&=-\cos \left( \frac{q-1}{M-1}\pi \right) , \quad q=1,2,\dots , M \end{aligned}$$

(36)

where N, M are the total number of sampling points along the two directions $\xi$ and η. Considering the boundary condition implementation illustrate above, it is important to note that two facing edges must have the same amount of grid points in order to avoid numerical discontinuities. Thus, an equal number of points along $\xi$ and η directions are set N = M. It should be noted that the only technique that allows to have a different number of points along x and y is the multi-domain technique, because a regular division that follows the external Cartesian system is imposed.

In general the mapping equations are applied to the equations of motion in terms of displacement parameters (see Sect. 2) and discretized at the master element level. Moreover each element boundary conditions are calculated as a function of the element location and connectivity in the mesh at issue, as in Fig. 3. Following the general guidelines of the GDQ implementation [44, 45, 47] the code computes four stiffness matrices for each element: ${\mathbf {K}}_{bb}^{(n)}$, ${\mathbf {K}}_{bd}^{(n)}$, ${\mathbf {K}}_{db}^{(n)}$ and ${\mathbf {K}}_{dd}^{(n)}$, for $n=1,2,\dots ,n_e$. In the dynamic case the mass matrix has to be also evaluated ${\mathbf {M}}_{dd}^{(n)}$, for $n=1,2,\dots ,n_e$. Furthermore the compatibility conditions have to be written in the coupling matrices ${\mathbf {K}}_{bb}^{(n,m)}$ and ${\mathbf {K}}_{bd}^{(n,m)}$, for $n,m=1,2,\dots ,n_e$.

After the discretization of the equation of motion for the generic element, the assembly procedure must be introduced in order to have the assembled matrix for the total system. The assembly procedure at hand follows the implementation steps presented in [111, 112]. Figure 5a shows a simple example of a global stiffness matrix for a mesh with two elements. The sketch shows that two elements have been considered in the decomposition and the two elements share an edge. In fact in the upper part $\overline{\mathbf {{K}}}_{b}$, boundary and compatibility conditions are collected, whereas in the lower part $\overline{\mathbf {{K}}}_{d}$ the domain equations for each element are located. It is pointed out that the connection between the elements is enforced by the boundary conditions only, in fact $\overline{\mathbf {{K}}}_{b}$ is composed of full matrices. On the contrary $\overline{\mathbf {{K}}}_{d}$ contains band matrices only. Using the same procedure the global mass matrix can be assembled as drawn in Fig. 5b. Since no concentrated masses are placed on the element boundaries the inertias are only related to the domain points.

Fig. 5

Global stiffness (a) and mass (b) matrices for a sample mesh made of two adjacent elements

Considering all that has been stated so far, the algebraic solution for the static and free vibration problem can be presented in the following. For the static problem, once the spatial derivatives of the fundamental and boundary equations are discretized the global set of algebraic equations become

$$ \left[ \begin{array}{ll} \overline{\mathbf {{K}}}_{bb} & \overline{\mathbf {{K}}}_{bd}\\ \overline{\mathbf {{K}}}_{db} & \overline{\mathbf {{K}}}_{dd} \end{array} \right] \left[ \begin{array}{l} {\mathbf {U}}_b \\ {\mathbf {U}}_d \end{array} \right] = \left[ \begin{array}{l} {\mathbf {Q}}_b \\ {\mathbf {Q}}_d \end{array} \right] $$

(37)

where ${\mathbf {U}}_b$, U _d are the domain and boundary functional values at all the sampling points of the current domain. With the same meaning of the symbols ${\mathbf {Q}}_b$, Q _d are the boundary and domain applied loads. By inverting the global stiffness matrix the system (37) can be solved. Furthermore it is possible to reduce the computational effort by means of static condensation. In other words it can be useful to rewrite the algebraic system (37) as

$$ \left( \overline{\mathbf {{K}}}_{dd} - \overline{\mathbf {{K}}}_{db}\overline{\mathbf {{K}}}_{bb}^{-1}\overline{\mathbf{{K}}}_{bd} \right) \overline{\mathbf {U}}_d = {\mathbf {Q}}_d -\overline{\mathbf {{K}}}_{db}\overline{\mathbf {{K}}}_{bb}^{-1}{\mathbf {Q}}_b $$

(38)

In this way the matrix of Eq. (37), that is $N^2\cdot n_e\cdot n_d$, is reduced in Eq. (38) as $(N-2)^2\cdot n_e\cdot n_d$. It should be noted that n _d is the number of equations in the current problem and n _e identifies the number of elements in the domain division. Due to the fact that the exact solution, used for the comparisons, is related to isotropic flexural plates [also known as Classical Plate Theory (CPT)], only three equations of the aforementioned Reissner-Mindlin plate theory are considered. In fact the the membrane and bending behaviors are uncoupled for isotropic Reissner-Mindlin plates. In all the other cases, that are not related to the comparison with the analytical solution, five equations are taken into account.

For the free vibration solution an eigenvalue problem is achieved after the well-known general assumption of variable separation

$${\mathbf {u}}({\mathbf {x},t}) = {\mathbf {U}}({\mathbf {x}})e^{i \omega t}$$

(39)

where the eigenvalues $\omega ^2$ and the eigenvectors ${\mathbf {U}}(\mathbf {x})$ are seek once the boundary conditions are imposed. A generalized eigenvalue problem is carried out

$$\left[ \begin{array}{ll} \overline{\mathbf {{K}}}_{bb} &{}\overline{\mathbf {{K}}}_{bd}\\ \overline{\mathbf {{K}}}_{db}& \overline{\mathbf {{K}}}_{dd} \end{array} \right] \left[\begin{array}{l} {\mathbf {U}}_b \\ {\mathbf {U}}_d \end{array}\right] = \omega ^2 \left[ \begin{array}{ll} {\mathbf {0}} &{\mathbf {0}} \\ {\mathbf {0}} & \overline{\mathbf {{M}}}_{dd}\end{array} \right] \left[ \begin{array}{l} {\mathbf {U}}_b \\{\mathbf {U}}_d \end{array} \right]$$

(40)

If the static condensation is worked out in the dynamic case, the computational speed increases and the results result to be more accurate. For the dynamic case is not possible to condensate the domain points, due to the unknown eigenvalues $\omega ^2$, so the boundary points have to be used

$$\left( {\bar{\bf{K}}}_{dd} - {\bar{\bf{K}}}_{db}{\bar{\bf{K}}}_{bb}^{-1}{\bar{\bf{K}}}_{bd} \right) {\mathbf{U}}_{d} = {\omega^2}{\bar{\bf{M}}}_{dd}{\mathbf{U}}_{d}$$

(41)

Now the natural frequencies of the structure $f=\omega /2\pi$ can be evaluated by solving the generalized eigenvalue problem (41).

4 Numerical applications

In the numerical applications a double parameter optimization is performed, as suggested by the authors in the work [36]. The shape parameter b and the stretching parameter α of the distribution are optimized. As far as the stretching parameter α is concerned, its aim is to reallocate the grid points of a given distribution in order to improve the numerical accuracy for the case under study. The stretching formulation is reported in the following for the sake of completeness

$$ {\xi _{p} = \left( 1-\alpha \right) \left( 3\bar{\xi }_{p}^2 -2\bar{\xi }_{p}^3 \right) + \alpha \bar{\xi }_{p} \quad {\text { for }}\quad {p} = 1,2,\dots ,N} {\eta _{q}} = \left( 1-\alpha \right) \left( {3\bar{\eta }}_{q}^2 -{2\bar{\eta }}_{q}^3 \right) + \alpha {\bar{\eta }}_{q} \quad \text { for }\quad{q} = 1,2,\dots ,M$$

(42)

The optimization procedure exploits the differentiation formula (25). A simple sketch of the implemented optimization procedure is shown in Algorithm 1. Before launching the optimization, the upper and lower bounds of the shape parameter b $\left[ b_{\min }, b_{\max } \right]$ and of the stretching parameter α $\left[ \alpha _{\min }, \alpha _{\max } \right]$ are defined. In order to perform the optimization, the algorithm needs a starting value for each parameter $b_0=0.5(b_{\max }+b_{\min })$ and $\alpha _0=0.5(\alpha _{\max }+\alpha _{\min })$. These values are taken as the middle values of their upper and lower bounds. After the choice of the RBF $\phi (r_j(x),b)$, that is used in the computation, the reference function must be set, to provide a target to the algorithm. The code defines as target function $\phi (r_1(x(\alpha _0)),\bar{b})$ where $\bar{b}=1+10^{-6}$. Then the program computes the initial point locations $x_i(\alpha _0)$ and the first order exact derivative for $\phi (r_1(x(\alpha _0)),\bar{b})$. Subsequently, the same procedure is performed for the chosen RBF and the differentiation matrix is computed. The algorithm starts iterating the two values of b and α until the difference between the exact derivative and the approximated one is lower than a fixed tolerance $\epsilon =10^{-4}$. Mathematically speaking

$${\Vert {{\mathbf {f}}^{(1)}_{1} - {\mathbf {D}}^{(1)}{\mathbf {f}}_{1}} \Vert} \le {\epsilon} , \text { for } \, {\epsilon} =10^{-4}$$

(43)

Finally the parameters b and α are optimized. With the use of the optimization procedure illustrated above some static and dynamic numerical applications are presented for isotropic and laminated composite plates.

In the following with the terms GDQFEM and RBFEM it is meant to represent the SFEM technique using either Langrange polynomials $\mathcal {L}$ or RBFs. The reader will find the two expressions frequently in the following sections.

4.1 Isotropic square plate: static problem

The first benchmark considers the deflections of a simply-supported square plate (a/b = 1) uniformly loaded. The aim of this test is to study the static behaviour of a square plate as a function of the number of grid points N per element for several meshes and type of basis function ϕ chosen. In particular a single element n _e  = 1, a two element n _e  = 2 regular and distorted meshes, a four element n _e  = 4 regular and distorted ones and a nine element n _e  = 9 regular mesh are considered. The sketches of each mesh are embedded within the corresponding figure, as depicted in Fig. 6.

Fig. 6

Relative error convergence of central deflections for a simply-supported isotropic square plate using several basis functions and meshes, varying the number of grid points N per element: a single element n _e  = 1, b two regular elements n _e  = 2, c two distorted elements n _e  = 2, d four regular elements n _e  = 4, e four distorted elements n _e  = 4, f nine regular elements n _e  = 9

The classic analytical solution for a thin rectangular plate (with a and b sides of the plate) is given by the following equation

$$w_{\text {exact}}\left( x=\frac{a}{2},y=\frac{b}{2} \right) = \sum _{n=1}^{\infty }\sum _{m=1}^{\infty } \frac{16 q_{0}}{nm\pi ^6D\left( \left( \frac{n}{a}\right) ^2 + \left( \frac{m}{b}\right) ^2 \right) ^2}\sin \left( \frac{n\pi }{2} \right) \sin \left( \frac{m\pi }{2} \right)$$

(44)

where q ₀ is the vertical load and $D=Eh^3/(12(1-\nu ^2))$ is the flexural stiffness. It must be underlined that the comparison is performed between two different theories. A FSDT theory is implemented in the code and the analytical solution refers to the Kirchhoff-Love model. If the FSDT analytical and numerical solutions were compared the results would be more accurate with respect to the ones obtained considering two different kinds of models as presented below.

In Fig. 6a–f the convergence of the relative error $\mathcal {E}=\left| w_{\text {numerical}}/w_{\text {exact}}-1 \right|$ of the central plate deflection is shown for several basis functions. The RBFs nomenclature $\phi _r$, for $r = 1,2,\dots ,19$ is taken from the previous paper by the authors [36], in which all the basis functions have been tested on doubly-curved laminated composite shells. In the present work the functions ϕ used in the computations are reported in Table 1.

Table 1 Radial basis functions used in the numerical applications found in literature [36]

According to the basis function chosen several convergence behavior can be observed. Considering Fig. 6a–f, that is related to a single element mesh, three different convergence rates are shown. The first one is given by the functions ϕ ₅, ϕ ₆, ϕ ₇, ϕ ₈, ϕ ₉, ϕ ₁₈ and ϕ ₁₉ that have a very fast convergence but their errors oscillate for a large number of points N, that changes function by function. The second behavior is given by ϕ ₄, ϕ ₁₂, ϕ ₁₃, ϕ ₁₅ and ϕ ₁₆ which need $N\ge 21$ in order to have an accurate solution, nevertheless they are stable when N increases. Even though some of them do not reach an accurate solution because the number of points per element is limited $N\le 31$, in this test. Finally the third behavior is given by the Lagrange polynomials $\mathcal {L}$, termed in the past GDQFEM solution [111, 112]. It can be noted that GDQFEM has a very fast and stable solution for any value of N. It is pointed out that the number of elements does not seem to influence the convergence rate for any basis function because the aforementioned functions continue to reach the maximum accuracy almost for the same amount of grid point N. On the contrary when a distortion is enforced the converge rate of any basis function decreases due to the mapping transformation.

In order to study the converge rate of all the considered basis functions as functions of the number of elements for a fixed number of points on each domain N the following tests are shown. Figure 7a––f show the relative errors for eight regular meshes, that are n _e  = 1, n _e  = 4, n _e  = 9, n _e  = 16, n _e  = 25, n _e  = 36, n _e  = 49, n _e  = 64 (regular means that the elements have a square shape) for 6 different degrees of the approximating basis polynomials, such as N = 5, N = 7, N = 9, N = 11, N = 13, N = 15. Figure 7a shows that using N = 5 is not sufficient when RBFs are used because none of the RBFs $\phi _r$ has an accurate solution for all the considered meshes, nevertheless GDQFEM does not have a good accuracy for a few elements but its error decreases when the number of elements increases, a similar behavior can be observed in weak form-based numerical techniques [83, 84]. Two distinct behaviors appear for N = 7 in Fig. 7b where a stable trend is observed when n _e increases using ϕ but the errors are higher with respect to the $\mathcal {L}$ one. The best RBFs for the current case are ϕ ₁₈ and ϕ ₁₉ which have a stable error that is around 10⁻², when the number of elements n _e increases. As the polynomial degree increases N > 7, some RBFs tend to have a similar trend to the GDQFEM one. In fact in Fig. 7e–f, a part from ϕ ₄ , ϕ ₁₂, ϕ ₁₅ and ϕ ₁₆ all the others have a similar behaviour with respect to $\mathcal {L}$. Since some basis functions have an ill-conditioned differentiation matrix for N > 13 in Fig. 7f) it can be seen that ϕ ₅ and ϕ ₁₄ become unstable and the solution is not accurate, whereas for the present case all the previously considered functions have a very accurate solution compared to GDQFEM. In conclusion, it is important to note that the basis functions which needed more points in order to be accurate (see Fig. 6a–f) are never accurate in the cases presented in Fig. 7a–f, because it was shown by Fig. 6a–f that at least N  = 21 was needed.

Fig. 7

Relative error convergence of central deflections for a simply-supported isotropic square plate using several basis functions, varying the number of elements n _e per mesh and fixing the number of grid points: a N = 5, b N = 7, c N = 9, d N = 11, e N = 13, f N = 15

4.2 Isotropic square plate: free vibration

In the second numerical benchmark the free vibrations of a simply supported isotropic square plate (a/b = 1) are considered. The aim of this test is to study the dynamic behaviour of several meshes as a function of the number of grid points N for each element and the type of basis function $\phi (r_j(x),b)$ chosen.

The classic analytical solution for a rectangular plate (with a and b sides of the plate) is given by the following equation

$$\begin{aligned} \omega _{nm} = \pi ^2\left( \left( \frac{n}{a}\right) ^2 + \left( \frac{m}{b} \right) ^2 \right) \sqrt{\frac{D}{\rho h}} \end{aligned}$$

(45)

where $D=Eh^3/12(1-\nu ^2)$ is the flexural stiffness and $\rho$ is the material density. Similarly to the previous case, in the dynamic case also the presented frequencies are related to the Kirchhoff-Love thin plate model, so the accuracy of the present technique would be better if the same two FSDT models were compared, even though for thin Reissner-Mindlin plates the solution is similar to the Kirchhoff–Love one, as demonstrated by the following numerical tests.

In Fig. 8, 9, 10 the relative error $\mathcal {E}=\left| \omega _{\text {numerical}}/\omega _{\text {exact}} - 1\right|$ of the first three circular frequencies are depicted for several basis functions, varying the number of elements in the given mesh. Five different meshes are considered in the following: a single element mesh $n_e=1$, a two element mesh $n_e=2$ regular and distorted, and a four element mesh $n_e=4$ regular and distorted. All the used meshes are embedded within each plot for the sake of clarity. Analogous results to Fig. 6a–f) are obtained. In particular it can be seen that some RBFs have a rapid and accurate solution within a tolerance below $10^{-3}$ when the number of grid points is limited and they have an analogous behavior with respect to Lagrange polynomials $\mathcal {L}$. As for the static cases their errors start to oscillate when $N$ is large, due to the ill-conditioning of the differentiation matrix. Simultaneously, the convergence rate of the other RBFs is slower and they also do not reach the same accuracy of the previous group, because they need more than 31 points in order to obtain an accurate solution. It should be noted that when Lagrange polynomials $\mathcal {L}$ are used the solution is always accurate, stable and has a very fast convergence, for both the first three frequencies.

Fig. 8

Relative errors of the first three frequencies for a simply-supported isotropic square plate using several basis functions with a $n_e=1$ mesh, varying the number of grid points $N$ per element

Fig. 9

Relative errors of the first three frequencies of a simply-supported isotropic square plate using several basis functions with a regular $n_e=2$ mesh (a-c) and a distorted one (d-f), varying the number of grid points $N$ per element

Fig. 10

Relative errors of the first three frequencies of a simply-supported isotropic square plate using several basis functions with a regular $n_e=4$ mesh (a–c) and a distorted one (d–f), varying the number of grid points $N$ per element

The number of elements does not play a fundamental role in the convergence of the present technique, nevertheless the mapping distortion reduces, as in the static case, the convergence trend.

Figure 11a–f shows the convergence trends, of the relative error ($\mathcal {E}=\left| \omega _{\text {numerical}}/\omega _{\text {exact}} - 1\right|$) for the fundamental circular frequency $\omega _1$, varying the number of elements for the same amount of grid points per element. Six regular meshes are considered: $n_e=1$, $n_e=4$, $n_e=9$, $n_e=16$, $n_e=25$, $n_e=36$, $n_e=49$, $n_e=64$, each of them represents the abscissa of any point in the depicted plots (Fig. 11a–f). The number of grid points considered are $N=5$, $N=7$, $N=9$, $N=11$, $N=13$, $N=15$ that refer to Fig. 11a–f, respectively. It is noted that for $N=5$ (Fig. 11a) only the GDQFEM solution is accurate within a relative error below $10^{-2}$ for any number of elements $n_e$. In particular, the GDQFEM accuracy tends to decrease when the number of elements increases. For $N\ge 7$ (Fig. 11b–f) the GDQFEM solution seems not to be affected by the number of elements used. As far as the RBFs are concerned, for $N=5$ none of them gives a good approximation. Therefore, they start to be accurate for $N\ge 7$ and their number changes according to the differentiation matrix ill-conditioning. In fact, the number of accurate RBFs that can be counted for $N=11$ is not the same for $N=13$ and $N=15$, where a couple of them have an ill-conditioned matrix for $N>15$.

Fig. 11

Relative error convergence of the fundamental frequency for a simply-supported isotropic square plate using several basis functions, varying the number of elements $n_e$ per mesh and fixing the number of grid points: a $N=5$, b $N=7$, c $N=9$, d $N=11$, e $N=13$, f $N=15$

In order to study the convergence of the present methodology the discrete spectrum analysis [83, 86, 120, 121] is performed for five different meshes and presented in Fig. 12a, c–f, while Fig. 12b) shows the discrete spectrum study of only GDQFEM. The solution is reported as functions of the exact solution $\omega _{\text {numerical}}/\omega _{\text {exact}}$ on the vertical axis. On the horizontal axis the non-dimensional mode $n$ number with respect to the total number of degrees of freedom $N_t=(N-2)^2n_e n_d$ is reported, where $n_d=3$ in this case because isotropic plates are studied. The same number of grid points $N=31$ is used as functions of the approximating polynomials and for all the considered meshes. It can be noted that only the GDQFEM solution has the initial part of the spectrum that is fairly well-resolved, in fact the black line lies on the horizontal axis, indicated by 1 and then the discrete frequencies corresponding to $n/N_t>0.05$ and $n/N_t>0.1$ exhibit an error that gradually increases. On the contrary RBFs have not stable spectra due to ill-conditioned differentiation matrix at higher modes. As far as the GDQFEM spectrum is concerned its discrete eigenvalues are larger in magnitude than the continuous (exact) ones, this indicates that the free vibration simulation overestimate the dynamic behavior of the plate. Whereas RBFEM tends to overestimate the vibration frequency when there are one $n_e=1$ or two $n_e=2$ mesh elements and the circular frequency is underestimated when four elements $n_e=4$ occur. It should be indicated that the upper part of the discrete spectra exhibit forty percent of error and the lower part thirty percent of error. Furthermore, the GDQFEM is very accurate for the first vibration modes but after $n/N_t>0.1$ the error exponentially grows, whereas some RBFs have a limited error that is more or less constant from the lower to the higher frequencies.

Fig. 12

Discrete spectra plots of the ratio between the numerical and the exact frequency for different meshes: a $n_e=1$, c $n_e=2$ regular, d $n_e=2$ distorted, e $n_e=4$ regular, f $n_e=4$ distorted, and b GDQFEM behavior with structured and distorted meshes

It should be noted that the four element meshes (Fig. 12e, f) seem more accurate than the two element meshes (Fig. 12c, d) this is due to the element distortion in the current meshes. In other words the four element mesh is composed of only regular elements (structured mesh), whereas the two element mesh has two rectangles, so one side of the elements is two times the other side. This aspect can be seen in Fig. 12b) where two different discretizations are used: a structured and non-structured one, such as square and rectangle divisions. The accuracy of the square divisions ($n_e=1$, $n_e=4$, $n_e=9$, $n_e=16$, $n_e=25$, $n_e=36$, $n_e=49$, $n_e=64$) are very similar among them, whereas the rectangular divisions ($n_e=2$, $n_e=8$, $n_e=32$) are almost superimposed but they have a lower accuracy. Therefore, this aspect explains the difference between Fig. 12c and e). Hence, the element distortion plays a fundamental role in the stability of the present technique. In fact, the two distorted meshes presented in Fig. 12d, e have a lower accuracy if compared to the structured ones.

4.3 Some computational remarks

The present tests showed a very important aspect. The converge of the numerical solutions is not always monotonic according to the number of grid points used. In particular, some RBFs reached an accurate solution with a less number of grid points with respect to the others which have a monotonic trend.

The discontinuous trends can be explained by the fact that increasing the number of points per element the differentiation matrix becomes ill-conditioned, as already explained in section 3.2. Thus, it is observed that the RBFs that have an oscillating error carry out several imaginary eigenvalues that are due to the non-symmetry of the stiffness matrix. This imaginary eigenvalues are not considered in the numerical solution because only the real eigenvalues are the real frequencies of the plates. So sorting out only the real frequencies the aforementioned graphs are presented.

On the contrary the coefficient matrices of $\phi _{12}$, $\phi _{15}$ and $\phi _{16}$ do not become ill-conditioned when the number of points increases. Effectively, their trend is always monotonic when $N$ increases.

Summarizing, only functions that have a monotonic trend should be used, nevertheless that is not completely true because the total number of degrees of freedom of these problems is $N^2 \cdot n_e \cdot n_d$, for $n_d=5$ in composite plate case and $n_d=3$ for the isotropic ones. Applying the kinematic condensation, in both static and dynamic case, the computational dimension can decrease but the degrees of freedom of a four element mesh $n_e=4$ are four times the ones of a single element $n_e=1$ and sometimes it cannot be solved due to computing memory issues. As a result RBF with a discontinuous convergence ($\phi _5$, $\phi _6$, $\phi _7$, $\phi _8$, $\phi _9$, $\phi _{18}$, $\phi _{19}$) should be used instead of the stable ones ($\phi _4$, $\phi _{12}$, $\phi _{13}$, $\phi _{15}$, $\phi _{16}$), because they can reach a good accuracy for less points. By changing the number of elements in the same problem, the same convergence rates are observed. In fact the SFEM convergence does not depend on how many elements appear in the mesh but it is functions of the RBF chosen and the number of grid points used. In other words, the convergence depends on how well the derivative is approximated inside each element.

For the sake of conciseness of the present paper a deep study on the use of a synthetic shape parameter is not investigated as was done in the previous work [36]. For further development on the subject the shape and stretching parameters calculated for several grid points $N$ are reported in Fig. 13a, b. Most of the RBFs have an oscillating value for both $b$ and $\alpha$. However, almost all of them with a large $N$ have a shape parameter that it almost equal to unity.

Fig. 13

Shape and stretching parameters optimization results for the tested RBFs varying the number of grid points N. (Color figure online)

4.4 Arbitrarily shaped plates: isotropic plates.

In the present section some arbitrarily shaped plates with a single element mesh are considered in the comparison. The plates are isotropic and the numerical results are compared in terms of the non-dimensional frequency $\Lambda = \omega \frac{a^2}{\pi ^2} \sqrt{\frac{\rho h}{D}}$, where $D=Eh^3/12(1-\nu ^2)$ is the flexural stiffness. The material density is indicated by ρ, the plate thickness is h and a is a geometric parameter. The reference article is the one by Bert and Malik [39], where thin isotropic plates have been studied within mapping-technique-based quadrature element formulation. The first comparison is based on a symmetric trapezoidal plate [39] where a/b = 3, b/c = 2.5. In the upper part of Table 2 the first ten dimensionless frequencies λ are shown. The RBFEM solution is compared also with a GDQFEM solution, already presented in the paper [112] for a single element mesh n _e  = 1 and N = 41 and two-dimensional FEM solution using a mesh of 13085 elements made of S8R 2D shell element type with 6 dofs per node. Two distinct boundary conditions are shown: the fully clamped condition (C–C–C–C) and the supported-clamped-supported-clamped (S–C–S–C) one, in which the supported edges are the sides parallel to the external Cartesian system, whereas the other two are clamped. It is noted that for each RBF the minimum number of points that achieve an accurate solution is used, according to the comparisons performed within the correspondent analytical solutions. Therefore N = 11 is used for ϕ ₅, ϕ ₆, ϕ ₇, ϕ ₉, N = 15 is used for ϕ ₈, ϕ ₁₈, N = 14, N = 33 and N = 31 is considered for ϕ ₁₂, ϕ ₁₅ and ϕ ₁₆ respectively. For the sake of conciseness not all the RBFs are shown in the present tables. It is pointed out, for instance, that using ϕ ₆ and ϕ ₇ a good agreement is observed using a less amount of points with respect to the GDQFEM solution. On the contrary some basis functions, such as ϕ ₉, ϕ ₁₂, ϕ ₁₅ have great errors for higher-order frequencies with respect to the given reference solutions. This aspect has been already shown by the discrete spectra of Fig. 12a–e, where the RBFs have problems with high-order modes.

Table 2 Arbitrarily shaped isotropic plates comparison with literature: symmetric trapezoidal and symmetric parabolic trapezoidal plates

The second example is also seized from the previous reference [39] where a symmetric parabolic trapezoidal plate with a/b = 3, b/c = 2.5 is taken into account. For the sake of completeness, the parabolic profile for the edges characterization is given as $x=a\frac{b^2-y^2}{b^2-c^2}$. Two cases are considered: a fully clamped (C–C–C–C) case and another one in which the plate is supported on the two straight edges and clamped on the other two (S–C–S–C). The results in terms of the frequency parameter λ are summarized in the lower part of Table 2. The solutions are compared to the works [2, 39] and the GDQFEM solution presented by the authors in the work [112] for n _e = 1 and N = 41. Also in the present case, the minimum number of points which allows each RBF to converge to the searched solution is given. Good agreement is observed both with respect to the classic results from the literature and considering a GDQFEM solution. For some basis functions, such as ϕ ₅, ϕ ₈, ϕ ₁₂ and ϕ ₁₅, the difference among the calculated frequencies increases when higher-order modes are computed.

4.5 Arbitrarily shaped plates: laminated composite

Some composite plates of arbitrary shape are investigated in the present section. In the first part three flat plates defined in curvilinear orthogonal coordinates are used. In case the reader wants to deep his knowledge about this topic, the works [67, 112] can be used as a reference. Moreover the same geometric parameters and mechanical properties presented in the work [112] are used in the following. The mechanical properties of the material are reported in Table 3, while the geometric parameters are summarized for the three plates in Table 4. The above defined materials and geometries nomenclature are considered in the following. The RBFEM meshes used in the computations at hand are the same as the ones depicted in the previous work by the authors [112].

Table 3 Materials used in the numerical calculations

Table 4 Geometric and mechanical properties of laminated composite arbitrarily shaped plates using curvilinear orthogonal coordinates

The first example deals with an elliptic plate that is clamped on two opposite edges and free on the other two (C-F-C-F). The present mesh is made of two elements n _e = 2 in order to map the elliptic profile correctly. The results in terms of the first ten free vibration frequencies are reported in the first part of Table 5, where not only the RBFEM solutions are summarized for several RBFs but also they are compared to FEM and GDQFEM solutions.

Table 5 Arbitrarily shaped laminated composite plates comparison with literature: elliptic, parabolic and bipolar plates

The second plate test concerns a parabolic plate clamped on two adjacent edges and free on the other two (F–F–C–C), with the mechanical and geometric properties summarized in the middle part of Table 4. It is noted that for the present case a single element mesh n _e  = 1 is used in the numerical calculations, because three points are the minimum number of points for drawing a parabolic curve on a plane. Hence, the results related to this case are reported in the middle part of Table 5.

The third benchmark considers a bipolar plate that is clamped on two opposite edges and free on the other two (C-F-C-F). In this case the mesh is made of eleven RBFEM elements n _e  = 11 due to the complexity of the given geometry. Once again the mechanical and geometric parameters and the numerical results of the bipolar plate are placed in Tables 4 and 5, respectively.

For all the above worked out numerical tests good agreement is observed for all the cases under study. As it was noticed in the previous examples also in these cases using certain RBFs, such as ϕ ₆ and ϕ ₇ it is possible to achieve an accurate solution with respect to GDQFEM and FEM ones using a small amount of grid points per element.

The last and new applications concern an elliptic plate with two holes, an elliptic plate with a linear crack and a plate made of elliptic and circular profiles (see Fig. 14). It should be noted that, computationally speaking, these three last applications deals with curved boundary conditions, element connectivity with sharp corner edges and curved inter-element edges. The elliptic plate mesh is shown in Fig. 14a). The plate at hand is composed of an ellipse with a = 2 m and b = 1 m, where a and b are the two semi-axis of the ellipse. The two holes are drawn at the same distance from the plate center of 0.5 m, the square sides are l = 0.5 m and the rectangle sides are l and 2l, as it can be seen from Fig. 14a. The structure is made of two laminae of Graphite-Epoxy with (30/45) orientations for a total plate thickness of h = 0.1 m, where $h_1=h_2=0.05$ m. The first ten frequencies are calculated and reported in Table 6 where a reference solution is obtained using Abaqus (a three dimensional solution with $\text {dofs}=1,\!402,\!140$ using 20 nodes brick elements and a two-dimensional one with $\text {dofs}=101,\!976$ using 8 nodes shell elements). Moreover, the RBFEM solution considering several basis functions is compared to a GDQFEM (Lagrange polynomials) solution using N = 15. It should be underlined that a different number of points is used for each RBF in order to achieve the best approximation for the case under study, as demonstrated in the first isotropic benchmarks. The first nine mode shapes are depicted in Fig. 15, using ϕ ₁₆ and N = 15.

Fig. 14

Geometries used in the computations: a elliptic plate with two holes, b elliptic plate with a linear crack (underlined in red), c plate made of an ellipse and a circle

Fig. 15

First nine mode shapes of a composite (30/45) elliptic plate with two holes: a square and a rectangle. The solution is calculated with ϕ ₁₆ and N = 15

Fig. 16

First nine mode shapes of a composite (30/60) elliptic plate with a linear crack. The solution is calculated with ϕ ₆ and N = 11

Fig. 17

First nine mode shapes of composite (30/65/45) plate made of an ellipse and a circle. The solution is calculated with ϕ ₁₆ and N = 21

Table 6 First ten frequencies for a composite (30/45) elliptic plate with two holes

The second test concerns an elliptic plate with a linear crack. The plate geometry considers the same elliptic shape of the previous example, but in the present case a non-symmetric linear crack is considered. The crack has a length of 1.5 m and it is underlined in red in Fig. 14b). The plate has a total thickness h = 0.1 m made of two laminae of equal thickness $h_1=h_2=0.05$ m of graphite-epoxy with (30/60) orientations. The first ten frequencies are written in Table 7 where the RBFEM numerical results for several basis functions using different number of grid points are compared to GDQFEM and FEM solutions. It is pointed out that the two FEM solutions are worked out with a three-dimensional mesh with $\text {dofs}=654,\!897$ and a two-dimensional one has $\text {dofs}=160,\!188$. It should be noted that for the case at hand the GDQFEM and RBFEM two-dimensional solutions are in good agreement with respect to the three-dimensional FEM one. Therefore, the given strong form solutions are more similar to a three-dimensional solution even though they are two-dimensional. The first nine mode shapes of the current structure as shown in Fig. 16, using ϕ ₁₆ and N = 11.

Table 7 First ten frequencies for a composite 30/60 elliptic plate with a linear crack

The third plate regards a structure composed of a half-circle and half-ellipse, as shown in Fig. 14c). The inner circle radius is R _i  =  0.5 m and the outer circle radius is R _e  = 1 m, while the inner semi-axes of the half-ellipse are a _i  = 1 m and b _i = 0.5 m and the outer semi-axes are a _e  = 2 m and b _e  = 1 m, respectively. The plate at hand has a (30/65/45) lamination scheme using Graphite-Epoxy composite material. The total plate thickness is h =  0.03 m and all the plies have the same thickness $h_1=h_2=h_3=0.01$ m. The first ten frequencies are reported in Table 8 for a three-dimensional and a two-dimensional FEM solutions. The first one is obtained using $\text {dofs}=3,\!588,\!276$ with 20 nodes brick elements and the second solution uses $\text {dofs}=67,\!764$ with 8 nodes shell elements. Moreover GDQFEM numerical results using N = 21 is considered for the sake of the comparison. In this case also, the RBFEM solution is carried out for different basis functions, which are applied within a fixed number of grid points, as in the previous example. The first nine mode shapes of the current structure as shown in Fig. 16, using ϕ ₁₆ and N = 21.

Table 8 First ten frequencies for a composite (30/65/45) plate made of an ellipse and a circle with a hole

5 Conclusion

A new numerical technique for solving laminated composite plates of arbitrary shape is introduced. After the well-known mesh generation procedure and mapping technique, the strong form of the partial differential system of equations is solved at the master element level. In particular several RBFs and Lagrange polynomials are used for the derivative calculations inside each element. The first numerical procedure is termed RBFEM and second one GDQFEM, for the sake of conciseness it is possible to generally call these kind of techniques SFEM in contrast to the well-known and more widespread weak form based methodologies which can be generally called WFEM or FEM.

Regarding the numerical applications the stability, accuracy and reliability of SFEM was shown for structured and non-structured meshes, different grid points and basis functions. All the results are in good agreement when compared to analytical, literature and FEM numerical solutions. Further development on the subject can be done as far as the shape parameters of the RBFs is concerned, moreover other basis functions can be employed for other numerical benchmarks.