Skip to main content
Springer Nature Link
Log in

Admissible-level \(\mathfrak {sl}_3\) minimal models

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

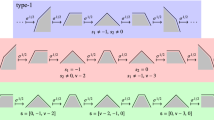
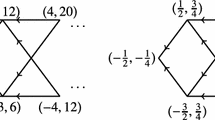Abstract

The first part of this work uses the algorithm recently detailed in Kawasetsu and Ridout (Commun Contemp Math 24:2150037, 2022. arXiv:1906.02935 [math.RT]) to classify the irreducible weight modules of the minimal model vertex operator algebra \({\textsf {L} }_{{\textsf {k} }}(\mathfrak {sl}_{3})\), when the level \({\textsf {k} }\) is admissible. These are naturally described in terms of families parametrised by up to two complex numbers. We also determine the action of the relevant group of automorphisms of \(\widehat{\mathfrak {sl}}_{3}\) on their isomorphism classes and compute explicitly the decomposition into irreducibles when a given family’s parameters are permitted to take certain limiting values. Along with certain character formulae, previously established in Kawasetsu (Adv Math 393:108079, 2021. arXiv:2003.10148 [math.RT]), these results form the input data required by the standard module formalism to consistently compute modular transformations and, assuming the validity of a natural conjecture, the Grothendieck fusion coefficients of the admissible-level \(\mathfrak {sl}_{3}\) minimal models. The second part of this work applies the standard module formalism to compute these explicitly when \({\textsf {k} }=-\frac{3}{2}\). This gives the first nontrivial test of this formalism for a nonrational vertex operator algebra of rank greater than 1 and confirms the expectation that the methodology developed here will apply in much greater generality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

Notes

  1. If we were considering coherent families of \(\mathrm {d}(\mathfrak {l})\)-modules instead of \(\mathfrak {l}\)-modules, then the Weyl reflection appearing here would be \(\mathrm {w}_{2}\).

  2. We remark that under the general definition in [51], all of these modules would be examples of relaxed highest-weight modules. However, in this case the nomenclature introduced here is convenient and so we shall adopt it, hoping that no confusion will arise.

  3. There is a well-known exception to this statement when \({\textsf {u} }\geqslant 3\) and \({\textsf {v} }=1\), so \({\textsf {k} }\in \mathbb {Z}_{\geqslant 0}\). Then, the positive-energy category coincides with \(\widehat{\mathscr {W}}_{{\textsf {u} },1}\) and the category of integrable highest-weight \(\widehat{\mathfrak {sl}}_{3}\)-modules; the latter is of course preserved by spectral flow.

  4. We shall generally drop the hat from affine Dynkin labels, trusting that this will not cause confusion.

  5. As we shall see, this arbitrary choice is convenient because the subsets of admissible weights classifying the relaxed, semirelaxed and highest-weight \({\textsf {A} }_{2} \left({\textsf {u} }, {\textsf {v} } \right)\)-modules then satisfy \(C_{{\textsf {u} },{\textsf {v} }}^2 \subseteq B_{{\textsf {u} },{\textsf {v} }}^1 \subset A_{{\textsf {u} },{\textsf {v} }}\).

  6. It is easy to check that \(\widehat{\lambda } \in C_{{\textsf {u} },{\textsf {v} }}^2\) implies that there are no triple intersections.

  7. We recall that the “−-type” quantum Hamiltonian reduction was introduced by Frenkel, Kac and Wakimoto in [40] for regular (principal) nilpotent elements. It differs from the usual “\(+\)-type” regular reduction in that it gauges the negative root vectors instead of the positive ones. Although both reductions give isomorphic W-algebras, the corresponding functors on modules are different. The reduction functor used in Theorem 5.1 is a generalisation of this −-type functor to all nilpotents due to Kac–Wakimoto [59] and Arakawa [60].

  8. We remark that this name, while quite standard, may be a little misleading. It does not refer to a 1-point correlation function of genus 1 in an appropriate conformal field theory, but rather to a chiral version where the trace is taken over a fixed module. In other words, this concept generalises the definition (5.1) of a character by inserting some fixed zero mode (usually unexponentiated!) inside the trace.

  9. The reader will no doubt recognise the action of \({\textsf {S} }\) and \({\textsf {T} }\) on \(\theta \) as a somewhat strange-looking generalisation of the usual formulae familiar from rational models. The terms involving complex arguments seem to be necessary to deal with the unusual automorphy factor that results from transforming Dirac combs.

  10. This second identity is well known for delta functions with real arguments. Here, as in many other applications of the standard module formalism, we assume that it may be extended to complex arguments. We expect that this formula can be established rigorously by finding the correct space of test functions to pair with and hope to pursue this in future work.

  11. This rigidity conjecture is very natural as all rational vertex operator algebras are known to produce rigid module categories (modular tensor categories even) [8] and a growing number of nonrational vertex operator algebras are also known to admit rigid module categories [32, 68,69,70,71,72]. There is, however, a known counterexample [73]. A modified Grothendieck fusion ring for this counterexample was studied in detail in [74].

  12. We thank an anonymous referee for this suggestion.

  13. That \(\widehat{\mathcal {L}}_{0}\) is the Grothendieck fusion unit follows directly from the standard Verlinde formula and the fact that the standard S-matrix is unitary.

References

  1. Kawasetsu, K., Ridout, D.: Relaxed highest-weight modules II: classifications for affine vertex algebras. Commun. Contemp. Math. 24, 2150037 (2022). arXiv:1906.02935 [math.RT]

    Article  MathSciNet  MATH  Google Scholar 

  2. Kawasetsu, K.: Relaxed highest-weight modules III: character formulae. Adv. Math. 393, 108079 (2021). arXiv:2003.10148 [math.RT]

    Article  MathSciNet  MATH  Google Scholar 

  3. Frenkel, I., Zhu, Y.: Vertex operator algebras associated to representations of affine and Virasoro algebras. Duke Math. J. 66, 123–168 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  4. Witten, E.: Non-abelian bosonization in two dimensions. Commun. Math. Phys. 92, 455–472 (1984)

    Article  ADS  MATH  Google Scholar 

  5. Gepner, D., Witten, E.: String theory on group manifolds. Nucl. Phys. B 278, 493–549 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  6. Verlinde, E.: Fusion rules and modular transformations in 2D conformal field theory. Nucl. Phys. B 300, 360–376 (1988)

    Article  ADS  MATH  Google Scholar 

  7. Moore, G., Seiberg, N.: Classical and quantum conformal field theory. Commun. Math. Phys. 123, 177–254 (1989)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. Huang, Y.-Z.: Vertex operator algebras and the Verlinde conjecture. Commun. Contemp. Math. 10, 103–154 (2008). arXiv:math/0406291 [math.QA]

    Article  MathSciNet  MATH  Google Scholar 

  9. Huang, Y.-Z.: Vertex operator algebras, the Verlinde conjecture, and modular tensor categories. Proc. Natl. Acad. Sci. USA 102, 5352–5356 (2005). arXiv:math/0412261 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Kac, V., Wakimoto, M.: Modular invariant representations of infinite-dimensional Lie algebras and superalgebras. Proc. Nat. Acad. Sci. USA 85, 4956–4960 (1988)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Koh, I., Sorba, P.: Fusion rules and (sub)modular invariant partition functions in nonunitary theories. Phys. Lett. B 215, 723–729 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  12. Kent, A. Infinite-dimensional algebras and the conformal bootstrap. PhD thesis, Department of Applied Mathematics and Theoretical Physics, Cambridge University (1986)

  13. Feigin, B., Frenkel, E.: Quantization of the Drinfeld–Sokolov reduction. Phys. Lett. B 246, 75–81 (1990)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Kac, V., Roan, S., Wakimoto, M.: Quantum reduction for affine superalgebras. Commun. Math. Phys. 241, 307–342 (2003). arXiv:math-ph/0302015

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Ridout, D.: \(\widehat{\mathfrak{sl} } \left(2 \right)_{-1/2}\): a case study. Nucl. Phys. B 814, 485–521 (2009). arXiv:0810.3532 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Creutzig, T., Ridout, D.: Modular data and Verlinde formulae for fractional level WZW models I. Nucl. Phys. B 865, 83–114 (2012). arXiv:1205.6513 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Creutzig, T., Ridout, D.: Modular data and Verlinde formulae for fractional level WZW models II. Nucl. Phys. B 875, 423–458 (2013). arXiv:1306.4388 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Creutzig, T., Ridout, D.: Relating the archetypes of logarithmic conformal field theory. Nucl. Phys. B 872, 348–391 (2013). arXiv:1107.2135 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Babichenko, A., Ridout, D.: Takiff superalgebras and conformal field theory. J. Phys. A 46, 125204 (2013). arXiv:1210.7094 [math-ph]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Ridout, D., Wood, S.: Bosonic ghosts at \(c=2\) as a logarithmic CFT. Lett. Math. Phys. 105, 279–307 (2015). arXiv:1408.4185 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Morin-Duchesne, A., Rasmussen, J., Ridout, D.: Boundary algebras and Kac modules for logarithmic minimal models. Nucl. Phys. B 899, 677–769 (2015). arXiv:1503.07584 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Canagasabey, M., Rasmussen, J., Ridout, D.: Fusion rules for the \(N=1\) superconformal logarithmic minimal models I: the Neveu–Schwarz sector. J. Phys. A 48, 415402 (2015). arXiv:1504.03155 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  23. Canagasabey, M., Ridout, D.: Fusion rules for the logarithmic \(N=1\) superconformal minimal models II: including the Ramond sector. Nucl. Phys. B 905, 132–187 (2016). arXiv:1512.05837 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Ridout, D., Snadden, J., Wood, S.: An admissible level \(\widehat{\mathfrak{osp} } \left(1 | \vert 2 \right)\)-model: modular transformations and the Verlinde formula. Lett. Math. Phys. 108, 2363–2423 (2018). arXiv:1705.04006 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. Babichenko, A., Kawasetsu, K., Ridout, D., Stewart, W.: Representations of the Nappi–Witten vertex operator algebra. Lett. Math. Phys. 111, 131 (2021). arXiv:2011.14453 [math-ph]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Fehily, Z., Ridout, D.: Modularity of Bershadsky–Polyakov minimal models. Lett. Math. Phys. 122, 46 (2022). arXiv:2110.10336 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Creutzig, T., Ridout, D.: Logarithmic conformal field theory: beyond an introduction. J. Phys. A 46, 494006 (2013). arXiv:1303.0847 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  28. Ridout, D., Wood, S.: The Verlinde formula in logarithmic CFT. J. Phys. Conf. Ser. 597, 012065 (2015). arXiv:1409.0670 [hep-th]

    Article  Google Scholar 

  29. Gaberdiel, M.: Fusion rules and logarithmic representations of a WZW model at fractional level. Nucl. Phys. B 618, 407–436 (2001). arXiv:hep-th/0105046

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. Ridout, D.: Fusion in fractional level \(\widehat{\mathfrak{sl} } \left(2 \right)\)-theories with \(k=-\tfrac{1}{2}\). Nucl. Phys. B 848, 216–250 (2011). arXiv:1012.2905 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Adamović, D., Pedić, V.: On fusion rules and intertwining operators for the Weyl vertex algebra. J. Math. Phys. 60, 081701 (2019). arXiv:1903.10248 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Allen, R., Wood, S. Bosonic ghostbusting—the bosonic ghost vertex algebra admits a logarithmic module category with rigid fusion (2022). arXiv:2001.05986 [math.QA]

  33. Arakawa, T., Futorny, V., Ramirez, L.: Weight representations of admissible affine vertex algebras. Commun. Math. Phys. 353, 1151–1178 (2017). arXiv:1605.07580 [math.RT]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Futorny, V., Morales, O., Ramirez, L. Simple modules for affine vertex algebras in the minimal nilpotent orbit. arXiv:2002.05568 [math.RT]

  35. Futorny, V., Křižka, L.: Positive energy representations of affine vertex algebras. Commun. Math. Phys. 383, 841–891 (2021). arXiv:2002.05586 [math.RT]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Futorny, V., Morales, O., Křižka, L. Admissible representations of simple affine vertex algebras. arXiv:2107.11128 [math.RT]

  37. Arakawa, T.: Rationality of admissible affine vertex algebras in the category \(\cal{O} \). Duke Math. J. 165, 67–93 (2016). arXiv:1207.4857 [math.QA]

    Article  MathSciNet  MATH  Google Scholar 

  38. Mathieu, O.: Classification of irreducible weight modules. Ann. Inst. Fourier (Grenoble) 50, 537–592 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zamolodchikov, A.: Infinite additional symmetries in two-dimensional conformal quantum field theory. Theoret. Math. Phys. 65, 1205–1213 (1985)

    Article  Google Scholar 

  40. Frenkel, E., Kac, V., Wakimoto, M.: Characters and fusion rules for W-algebras via quantized Drinfeld–Sokolov reduction. Commun. Math. Phys. 147, 295–328 (1992)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Arakawa, T., van Ekeren, J.: Modularity of relatively rational vertex algebras and fusion rules of principal affine \(W\)-algebras. Commun. Math. Phys. 370, 205–247 (2019). arXiv:1612.09100 [math.RT]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. Zhu, Y.: Modular invariance of characters of vertex operator algebras. J. Am. Math. Soc. 9, 237–302 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  43. Adamović, D.: Realizations of simple affine vertex algebras and their modules: the cases \(\widehat{sl(2)}\) and \(\widehat{osp(1,2)}\). Commun. Math. Phys. 366, 1025–1067 (2019). arXiv:1711.11342 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  44. Semikhatov, A. Inverting the Hamiltonian reduction in string theory. In: 28th International Symposium on Particle Theory, Wendisch-Rietz, Germany, pp. 156–167 (1994). arXiv:hep-th/9410109

  45. Adamović, D., Creutzig, T., Genra, N. Relaxed and logarithmic modules of \(\widehat{\mathfrak{sl}_3}\). arXiv:2110.15203 [math.RT]

  46. Adamović, D., Kawasetsu, K., Ridout, D.: A realisation of the Bershadsky-Polyakov algebras and their relaxed modules. Lett. Math. Phys. 111, 38 (2021). arXiv:2007.00396 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  47. Adamović, D.: A construction of admissible \(A_1^{\left(1\right)}\)-modules of level \(-\frac{4}{3}\). J. Pure Appl. Algebra 196, 119–134 (2005). arXiv:math.QA/0401023

    Article  MathSciNet  MATH  Google Scholar 

  48. Creutzig, T., Ridout, D., Rupert, M. A Kazhdan–Lusztig correspondence for \(L_{-3/2}(\mathfrak{sl}_3)\). arXiv:2112.13167 [math.RT]

  49. Fernando, S.: Lie algebra modules with finite-dimensional weight spaces. I. Trans. Am. Math. Soc. 322, 757–781 (1990)

    MathSciNet  MATH  Google Scholar 

  50. Gorelik, M., Kac, V.: On simplicity of vacuum modules. Adv. Math. 211, 621–677 (2007). arXiv:math-ph/0606002

    Article  MathSciNet  MATH  Google Scholar 

  51. Ridout, D., Wood, S.: Relaxed singular vectors, Jack symmetric functions and fractional level \(\widehat{\mathfrak{sl} } \left(2 \right)\) models. Nucl. Phys. B 894, 621–664 (2015). arXiv:1501.07318 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  52. Kac, V., Wakimoto, M.: Classification of modular invariant representations of affine algebras. In: Infinite-Dimensional Lie Algebras and Groups (Luminy-Marseille. 1988), volume 7 of Advanced Series in Mathematical Physics, pp. 138–177. World Scientific, New Jersey (1989)

  53. Joseph, A.: On the associated variety of a primitive ideal. J. Algebra 93, 509–523 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  54. Adamović, D.: A realization of certain modules for the \(N=4\) superconformal algebra and the affine Lie algebra \(A_2^{(1)}\). Transform. Groups 21, 299–327 (2016). arXiv:1407.1527 [math.QA]

    Article  MathSciNet  MATH  Google Scholar 

  55. Adamović, D., Milas, A., Wang, Q. On parafermion vertex algebras of \(\mathfrak{s}\mathfrak{l}(2)_{-3/2}\) and \(\mathfrak{s}\mathfrak{l} (3)_{-3/2}\). Commun. Contemp. Math. 24, 2050086 (2022). arXiv:2005.02631 [math.QA]

  56. Semikhatov, A. A note on the logarithmic \(W_3\) octuplet algebra and its Nichols algebra. arXiv:1301.2227 [math.QA]

  57. Kac, V., Wakimoto, M.: A remark on boundary level admissible representations. C. R. Acad. Sci. Paris Sér. I Math. 355, 128–132 (2017). arXiv:1612.07423 [math.RT]

    Article  MathSciNet  MATH  Google Scholar 

  58. Kawasetsu, K., Ridout, D.: Relaxed highest-weight modules I: rank \(1\) cases. Commun. Math. Phys. 368, 627–663 (2019). arXiv:1803.01989 [math.RT]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  59. Kac, V., Wakimoto, M.: On rationality of W-algebras. Transform. Groups 13, 671–713 (2008). arXiv:0711.2296 [math-ph]

    Article  MathSciNet  MATH  Google Scholar 

  60. Arakawa, T. Representation theory of \(W\)-algebras, II: Ramond twisted representations. In Exploring New Structure and Natural Constructions in Mathematical Physics, volume 61 of Advanced Studies in Pure Mathematics, pp. 51–90, Tokyo, 2011. Mathematical Society of Japan. arXiv:0802.1564 [math.QA]

  61. Kac, V., Wakimoto, M.: Quantum reduction and representation theory of superconformal algebras. Adv. Math. 185, 400–458 (2004). arXiv:math-ph/0304011

    Article  MathSciNet  MATH  Google Scholar 

  62. Arakawa, T.: Representation theory of superconformal algebras and the Kac–Roan–Wakimoto conjecture. Duke Math. J. 130, 435–478 (2005). arXiv:math-ph/0405015

    Article  MathSciNet  MATH  Google Scholar 

  63. Arakawa, T., van Ekeren, J. Rationality and fusion rules of exceptional W-algebras. arXiv:1905.11473 [math.RT]

  64. Perše, O.: Vertex operator algebras associated to certain admissible modules for affine Lie algebras of type \(A\). Glas. Mat. Ser. III(43), 41–57 (2008). arXiv:0707.4129 [math.QA]

    Article  MathSciNet  MATH  Google Scholar 

  65. Beem, C., Lemos, M., Liendo, P., Peelaers, W., Rastelli, L., van Rees, B.: Infinite chiral symmetry in four dimensions. Commun. Math. Phys. 336, 1359–1433 (2015). arXiv:1312.5344 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  66. Adamović, D.: A realization of certain modules for the \(N=4\) superconformal algebra and the affine Lie algebra \(A_2^{(1)}\). Transform. Groups 21, 299–327 (2016). arXiv:1407.1527 [math.QA]

    Article  MathSciNet  MATH  Google Scholar 

  67. Arakawa, T., Kawasetsu, K. Quasi-lisse vertex algebras and modular linear differential equations. In: Lie Groups, Geometry and Representation Theory, volume 326 of Progress in Mathematics, pp. 41–57. Birkhäuser/Springer (2018). arXiv:1610.05865 [math.QA]

  68. Tsuchiya, A., Wood, S.: The tensor structure on the representation category of the \(\cal{W} _p\) triplet algebra. J. Phys. A 46, 445203 (2013). arXiv:1201.0419 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  69. Creutzig, T., Jiang, C., Orosz Hunziker, F., Ridout, D., Yang, J.: Tensor categories arising from the Virasoro algebra. Adv. Math. 380, 107601 (2021). arXiv:2002.03180 [math.RT]

    Article  MathSciNet  MATH  Google Scholar 

  70. Creutzig, T., Yang, J.: Tensor categories of affine Lie algebras beyond admissible levels. Math. Ann. 380, 1991–2040 (2021). arXiv:2002.05686 [math.QA]

    Article  MathSciNet  MATH  Google Scholar 

  71. Creutzig, T., McRae, R., Yang, J.: On ribbon categories for singlet vertex algebras. Commun. Math. Phys. 387, 865–925 (2021). arXiv:2007.12735 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  72. Creutzig, T., McRae, R., Yang, J. Tensor structure on the Kazhdan–Lusztig category for affine \(\mathfrak{gl}(1|1)\). Int. Math. Res. Not. (to appear). arXiv:2009.00818 [math.QA]

  73. Gaberdiel, M., Runkel, I., Wood, S.: Fusion rules and boundary conditions in the \(c=0\) triplet model. J. Phys. A 42, 325403 (2009). arXiv:0905.0916 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  74. Ridout, D., Wood, S.: Modular transformations and Verlinde formulae for logarithmic \(\left( p_+, p_- \right)\)-models. Nucl. Phys. B 880, 175–202 (2014). arXiv:1310.6479 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  75. Li, H.: The physics superselection principle in vertex operator algebra theory. J. Algebra 196, 436–457 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  76. Creutzig, T., Ridout, D., Wood, S.: Coset constructions of logarithmic \(\left(1, p \right)\)-models. Lett. Math. Phys. 104, 553–583 (2014). arXiv:1305.2665 [math.QA]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  77. Creutzig, T.: Logarithmic W-algebras and Argyres–Douglas theories at higher rank. J. High Energy Phys. 2018, 188 (2018). arXiv:1809.01725 [hep-th]

Download references

Acknowledgements

KK’s research is partially supported by the Australian Research Council Discovery Project DP160101520, MEXT Japan “Leading Initiative for Excellent Young Researchers (LEADER)”, JSPS Kakenhi Grant numbers 19KK0065 and 21K3775. DR’s research is supported by the Australian Research Council Discovery Projects DP160101520 and DP210101502, as well as an Australian Research Council Future Fellowship FT200100431. SW’s research is supported by the Australian Research Council Discovery Project DP160101520 and the Humboldt Fellowship for Experience Researchers GBR-1212053-HFST-E.

Author information

Authors and Affiliations

  1. Priority Organization for Innovation and Excellence, Kumamoto University, Kumamoto, 860-8555, Japan

    Kazuya Kawasetsu

  2. School of Mathematics and Statistics, University of Melbourne, Parkville, 3010, Australia

    David Ridout

  3. School of Mathematics, Cardiff University, Cardiff, CF24 4AG, UK

    Simon Wood

Authors
  1. Kazuya Kawasetsu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. David Ridout
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Simon Wood
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to David Ridout.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kawasetsu, K., Ridout, D. & Wood, S. Admissible-level \(\mathfrak {sl}_3\) minimal models. Lett Math Phys 112, 96 (2022). https://doi.org/10.1007/s11005-022-01580-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11005-022-01580-9

Keywords

Mathematics Subject Classification