Abstract
A logic of grounding where what is grounded can be a collection of truths is a “many-many” logic of ground. The idea that grounding might be irreducibly many-many has recently been suggested by Dasgupta (2014). In this paper I present a range of novel philosophical and logical reasons for being interested in many-many logics of ground. I then show how Fine’s State-Space semantics for the Pure Logic of Ground (plg) can be extended to the many-many case, giving rise to the Pure Logic of Many-Many Ground (plmmg). In the second, more technical, part of the paper, I do two things. First, I present an alternative formalization of plg; this allows us to simplify Fine’s completeness proof for plg. Second, I formalize plmmg using an infinitary sequent calculus and prove that this formalization is sound and complete.






Similar content being viewed by others
Notes
Interestingly, Bolzano took a many-many notion of grounding as basic; the only discussion of the many-many character of Bolzano’s notion with which I am familiar is [5].
We will see how this is related to Fine’s official formulation of the State-Space Semantics later, in Section 3.
The above was an account of weak full ground. A more detailed account of the various notions of ground will come later in Section 3.
“Higher-order” in the sense that we allow the assumption and discharge of sequents.
We might take the collections to be pluralities of sentences, with the proviso that we allow empty pluralities.
Note that a sequent is not a sentence. For this reason there are no iterated grounding claims, i.e., claims of the form “ Γ grounds that (Δ grounds Θ)”.
It does not follow from this that there is some Θ such that Γ,Θ is a strict full ground of Δ. If the latter is the case Γ is a partial strict ground of Δ. For more information about the intended interpretation of these sequents and further distinctions of ground the reader is referred to [15, pp. 3–4], and especially [14, pp. 50–54].
While this picture of many-many grounding is metaphorical the way non-distributivity comes about in the official semantics is not dissimilar.
Dasgupta’s motivations for many-many grounding trade heavily on considerations of relevance [10]. One can consider “the wall” as giving the “abstract core” of Dasgupta’s examples.
Think of a Euthyphro question: “Why is the action beloved by the Gods?”
“Therefore” is not intended as a sentential operator here. Rather, think of it as indicating that p 0, p 1,… are inferred from q 0, q 1,… in a particularly explanatory way. Note that this means that p 0, p 1,… (that is, each p i ) and q 0, q 1,… (that is, each q i ) are asserted.
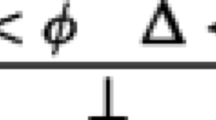
This suggests that we read a sequent Γ < Δ as the claim that there is an explanatory argument from Γ to Δ.
By focusing on the case of mathematical structuralism I am not suggesting that Dasgupta’s own motivations for many-many ground are flawed; they do, however, require rather more set-up and they are harder to model formally. Dasgupta defends comparativism in [8]; he defends qualitativism in [9]. He argues that comparativism and qualitativism require many-many ground in [10].
I do not mean to suggest that this is the only view that could be called “mathematical structuralism”.
What drives this example is the existence of indiscernible objects. I should note that Dasgupta is at pains—and rightly so, in my opinion—to point out that his motivations for many-many grounding do not require indiscriminable objects [10, p. 10]. But that does not mean that when there are indiscriminable objects we cannot use this fact to make a case for many-many grounding. Similar cases can be made for non-mathematical subject-matters: points in space (at least if space were Euclidean) and entangled electrons are two interesting cases.
This, of course, would only give us a case of weak full ground. Later, in Section 4.2, we give a plausible example of strict full grounding of collections of truths about the complex numbers.
There are two ways of thinking about what it takes to have a thoroughgoing structuralism. (Cf. Fine’s distinction between a D-project and an E-project [13, pp. 730–32].) The idea expounded here is that we have structuralism enough if all truths are grounded in the wholly structural. It then does not matter if in order to specify the wholly structural we have to make a bunch of claims that are not themselves wholly structural. But one might demand more (or at any rate, something else): one might ask for a specification of the wholly structural in terms not involving anything non-structural. One might want the language of the “Book of the World” [26] to be incapable of making any non-structural statements. (I hasten to add that the present use of the term “structural” must not be confused with Sider’s own use of the term.)
There is an interesting connection here with Fine’s notions of being constitutive of reality and being factual [16]. Once we allow many-many grounding it is natural to take these notions, too, to be variable-arity, non-distributive operators. Relatedly, Saucedo [22] has advocated that we adopt a non-distributive notion of fundamentality. This is not the place to discuss this further.
In a pure logic of ground the only logical operators one deals with are the various grounding operators. In an impure logic of ground, on the other hand, one considers also other logical operators, such as conjunction, disjunction, and negation. plg and plmmg are pure logics. The logics developed in [6, 25] are impure.
See [14, pp. 63–67] for more on this.
Here is a way of expressing this in question-and-answer form: “ ϕ 0, ϕ 1,…? No way! Why? Because ψ 0, ψ 1,….”
This treatment is, e.g., given in [17]. This is perhaps especially plausible in cases where it seems indeterminate whether ϕ.
I hope to expand on the impure logic of ground elsewhere.
This clause differs from the clause given in [15]. Fine only requires that there be some R 0, R 1,… such that \(P, R_{0}, R_{1}, {\ldots } \leq _{\mathcal {F}} Q\). Since we demand that \(\mathcal {V} \) is closed under π there is, for us, no difference between the two formulations. Since Fine’s formalization of plg is sound and complete with respect to full models it makes no difference to his formalization of plg either. There is, however, a difference in the higher-order setting developed in Section 7. See the discussion of (Unity) in Section 5.3 below.
Since sequents are not sentences it is admittedly somewhat strange to say that they are true in model, but for convenience we will continue to write in this way.
If we did not demand that \(\mathcal {V}\) be closed under π, the right-hand side of this clause should instead read: “there are some R 0, R 1,… such that \(P_{0}, P_{1}, \ldots , R_{0}, R_{1}, {\ldots } \leq _{\mathcal {F}} Q_{0}, Q_{1}, \ldots \)”. Cf. footnote 26 above. In the second part of the paper we will not quite demand that \(\mathcal {V}\) is closed—it suffices to impose a weaker condition.
For the purposes of the completeness proof we will later (Section 6) consider a more expressive language and this will require a subtler treatment of consequence; for now this will do.
Strict Squeezing—the principle that results if we replace ≤ with < uniformly—is also valid.
A proof is given in Proposition 6.
This is the clause used in [14].
As an anonymous reviewer did.
There is a related worry for Undercut.
Thanks to Kit Fine and Shamik Dasgupta for discussion on this point.
One might think that there was a simpler problem with plmmg. The following inference—call it (RRW) for restricted right weakening—is valid in plmmg:
$$(\text{RRW}) \quad\frac{\Gamma < \Delta} {\Gamma < \Gamma, \Delta} $$An instance of (RRW) is the following. Suppose it is raining. Then the truth that it is raining grounds the truth that is raining or snowing. (RRW) then ensures that the truths (plural), (it is raining or snowing, it is raining) are grounded in the truth that it is raining. We can put this in question and answer form: “It is raining or snowing. It is raining. Why? It is raining” Is this a good, non-circular explanation?
It is not obvious to me that this case is problematic—even on a conception of grounding as explanation. First, the same phenomenon arises in the many-one impure case. The conjunctive truth ((It is raining or snowing) ∧ it is raining) is grounded in the truth that it is raining. That does not seem objectionably circular. Second, part of the oddness one feels with a case like this might be because one has not wholly shed one’s commitment to distribution. In saying that the truths (it is raining or snowing, it is raining) together are grounded in the truth that it is raining, one is not committed to the truths taken on their own being grounded in the truth that it is raining. These considerations are hardly decisive; maybe (RRW) should be rejected on a conception of grounding as explanation. I do take the considerations to show that (RRW) is not obviously problematic on a conception of grounding as explanation. Thanks to an anonymous reviewer for making me realize that this case needs discussion.
For the purposes of this conjecture assume that every truth is ultimately grounded in some ungrounded truths. It is possible to rephrase the conjecture to allow the case where we have infinitely descending chains of ground.
I am grateful to an anonymous reviewer for raising this objection.
Since we do not have quantification into sentence position, (Unity) is not properly expressed in this form. But using the proof-theoretic framework developed in Section 7 we can express (Unity) in the form of a rule:
$$\begin{array}{c} \frac{}{p \leq \Delta}1\quad \frac{}{\Delta \leq p}2\\ {\mathcal{E}}\\ \qquad\qquad\frac{\alpha}{\alpha}1,2, \text{ Unity } \end{array} $$here p is a sentence that does not occur in Δ and does not occur in other undischarged premisses of the argument \(\mathcal {E}\).
As noted in foonote 26 this can be done by complicating the semantics and proof-theory for plmmg.
Somewhat picturesquely one can say that (Unity) expresses a sort of “local monism”: whenever we have some truths ϕ 0, ϕ 1,… we can always consider these truths “as one”—as “facets” of the truth ⊓{ϕ 0, ϕ 1,…}.
To see this we use the following fact about plg. (Unless the reader is already familiar with plg and the canonical model construction, return to this footnote after having read Section 10.) Observe that if \(\{\Delta \leq \sqcap \Delta \} \cup S\) is a consistent set of sequents in the language of plg, then \(T= \{\Delta \leq \sqcap \Delta \} \cup \{p \leq \sqcap \Delta \} \cup S\), where p is a fresh sentence letter, is also a consistent set of sequents. (Since “ ⊓” is not part of the language of plg think of ⊓Δ as a distinguished atomic sentence.) But the canonical model for T contains a verifier for ⊓Δ that is not a fusion of verifiers of Δ.
It is possible to dispense with a separate category of determinates. Using higher-order rules one can characterize what it is for an atom to be verifiable in only one way. Since doing this would make the formalism more unwieldy we opt for using a syntactically separate category of determinates.
An alternative formulation is possible. We could treat arguments as labeled directed hypergraphs. In that case the rules of Collection and Thinning would not be required.
This is just as it is in Fine’s formalization of plg.
References
Bliss, R. (2014). Viciousness and circles of ground. In Metaphilosophy 45.2 (pp. 245–256).
Bliss, R. (2013). Viciousness and the structure of reality. In Philosophical studies 166.2 (pp. 399–418).
Burgess, J.P. (1999). Book Review: Stewart Shapiro. Philosophy of Mathematics: Structure and Ontology. In Notre Dame Journal of Formal Logic 40.2.
Cameron, R.P. (2008). Turtles all the way down: regress, priority and fundamentality. In The Philosophical Quarterly 58.230 (pp. 1–14).
Cellucci, C. (1987). Bolzano and Multiple-Conclusion Logic. InternationalWorkshop (Firenze, 16-19 Settembre 1987). In Bolzano’s Wissenschaftslehre, 1837–1987 (pp. 179–189): Librarie Droz.
Correia, F. (2010). Grounding and Truth-functions. In Logique et Analyse 53.211 (pp. 251–279).
Correia, F. (2014). Logical grounds. In Review of Symbolic Logic 7.1 (pp. 31–59).
Dasgupta, S. (2013). Absolutism vs comparativism about quantity. In Oxford Studies in Metaphysics 8 (pp. 105–148).
Dasgupta, S. (2009). Individuals: An essay in revisionary metaphysics. In Philosophical Studies 145.1 (pp. 35–67).
Dasgupta, S. (2014). On the plurality of grounds. In Philosophers’ Imprint 14.20 (pp. 1–28).
deRosset, L. (forthcoming). Better semantics for the pure logic of ground. In Analytic Philosophy.
deRosset, L. (2013). Grounding explanations. In Philosophers’ Imprint 13.7 (pp. 1–26).
Fine, K. (2013). Fundamental truth and fundamental terms. In Philosophy and Phenomenological Research 87.3 (pp. 725–732).
Fine, K. (2012). Guide to ground. In Correia, F., & Schnieder, B. (Eds.) Metaphysical Grounding. Chap. 1 (pp. 37–80): Cambridge University Press.
Fine, K. (2012). The pure logic of ground. In The Review of Symbolic Logic 5.1 (pp. 1–25).
Fine, K. (2001). The question of realism. In Philosophers’ Imprint 1.1 (pp. 1–30).
Fine, K. (2014). Truth-maker semantics for intuitionistic logic. In Journal of philosophical logic 43.2-3 (pp. 549–577).
Keränen, J. (2001). The identity problem for realist structuralism. In Philosophia Mathematica 9 (pp. 308–330).
Litland, J.E. (2015). Grounding, explanation, and the limit of internality. In Philosophical Review 124.4 (pp. 481–533).
Litland, J.E. (forthcoming). Grounding ground. In Oxford studies in metaphysics.
Pruss, A. (2009). The Leibnizian cosmological argument. In The Blackwell Companion to natural theology (pp. 24–100).
Saucedo, R. Collective allism. In Unpublished manuscript.
Schaffer, J. (2015). Grounding in the Image of Causation. In Philosophical Studies. doi:10.1007/s11098-014-0438-1 (pp. 0031–8116).
Schaffer, J. (2003). Is there a fundamental level? In Nous 37.3 (pp. 498–517).
Schnieder, B. (2011). A logic for “because”. In Review of Symbolic Logic 4.3 (pp. 445–465).
Sider, T. (2012). Writing the book of the World. Oxford University Press.
Author information
Authors and Affiliations
Corresponding author
Additional information
Material from this paper was presented at a Workshop on Metaphysical Explanation at the University of Neuchâtel, June 23, 2013. Thanks to the participants there, especially Kit Fine and Shamik Dasgupta, for challenging questions that have much improved the paper. Thanks to Øystein Linnebo for asking the question that prompted the present inquiry. Thanks to Sam Roberts for many helpful suggestions and to Louis deRosset for comments on an earlier draft. Special thanks are due to an anonymous referee whose extremely detailed and constructively critical comments led me to a completeness proof for the infinitary case and then to a significant simplification of that completeness proof.
Rights and permissions
About this article
Cite this article
Litland, J.E. Pure Logic of Many-Many Ground. J Philos Logic 45, 531–577 (2016). https://doi.org/10.1007/s10992-015-9386-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-015-9386-2