Semiparametric inference for a two-stage outcome-dependent sampling design with interval-censored failure time data

Abstract

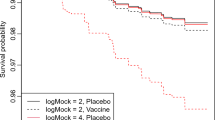
We propose a two-stage outcome-dependent sampling design and inference procedure for studies that concern interval-censored failure time outcomes. This design enhances the study efficiency by allowing the selection probabilities of the second-stage sample, for which the expensive exposure variable is ascertained, to depend on the first-stage observed interval-censored failure time outcomes. In particular, the second-stage sample is enriched by selectively including subjects who are known or observed to experience the failure at an early or late time. We develop a sieve semiparametric maximum pseudo likelihood procedure that makes use of all available data from the proposed two-stage design. The resulting regression parameter estimator is shown to be consistent and asymptotically normal, and a consistent estimator for its asymptotic variance is derived. Simulation results demonstrate that the proposed design and inference procedure performs well in practical situations and is more efficient than the existing designs and methods. An application to a phase 3 HIV vaccine trial is provided.

Appendix: Proofs of Theorems 1 and 2

In the appendix, we sketch the proofs of Theorems 1 and 2. Let $O\,=\,\left\{ Y=\{U,\,V,\,\Delta _1=I(T\le U),\,\Delta _2=I(U<T\le V)\},\, RZ,\, R\right\}$ denote a single observation, where U and V are two random examination times, Z is the p-dimensional covariate vector and R is the indicator of an observation being in the validation sample. The following regularity conditions are needed for proving the theorems:

• (C1) There exists $\eta >0$ such that $P(V-U\ge \eta )=1$. The union of the supports of U and V is contained in the interval $[\sigma ,\tau ]$, where $0<\sigma<\tau <+\infty$.

• (C2) The distribution of Z, denoted by $G_Z(z)$, has a bounded support and is not concentrated on any proper subspace of $R^p$.

• (C3) For $r=1$ or 2, the function $\Lambda _0(t)\in \mathcal {M}$ is continuously differentiable up to order r in $[\sigma ,\tau ]$ with the first derivative being strictly positive, and satisfies $\alpha ^{-1}<\Lambda _0(\sigma )<\Lambda _0(\tau )<\alpha$ for some positive constant $\alpha$. Also $\beta _0$ is an interior point of $\mathcal {B}$, a compact subset of $R^p$. $\mathcal {M}$ and $\mathcal {B}$ are defined in Sect. 3.

• (C4) The conditional density g(u, v|z) of (u, v) given z has bounded partial derivatives with respect to u and v, and the bounds of these partial derivatives do not depend on (u, v, z).

• (C5) $E\{\mathrm{var}(Z|U)\}$ and $E\{\mathrm{var}(Z|V)\}$ are positive definite.

These conditions are commonly used in the studies of interval-censored data (e.g. Huang and Wellner 1997; Huang and Rossini 1997; Zhang et al. 2010). In addition, similarly as in Zeng and Lin (2014), one can show that the conclusions of Theorems 1&2 hold under the proposed sampling scheme if they hold under independent sampling. Specifically, Zeng and Lin (2014) in their “Appendix” established the following result under general two-phase cohort studies based on Le Cam’s third lemma: the consistency and asymptotic normality of MLE hold under the sampling mechanism satisfying their condition (C.6) if they hold under independent sampling. It is easy to verify that our two-stage ODS scheme satisfies the condition (C.6) in Zeng and Lin (2014) with

$$\begin{aligned} p(1;y)= & {} I(y\in A_1)[p_0+(1-p_0)p_1]+I(y\in A_2)[p_0+(1-p_0)p_2]\\&+I(y\in A_3)p_0+I(y\in A_4)p_0, \end{aligned}$$

where $y=\{u,v,\delta _1,\delta _2\}$ is the outcome, $\{A_1,A_2,A_3,A_4\}$ are the four strata defined based on the outcome given in (1), $p_0$ is the sampling fraction of the SRS component, and $p_1$ and $p_2$ are the sampling fraction of the supplemental components from the two tail strata $A_1$ and $A_2$ respectively. Thus, we assume in the following that the observations $\{O_i,\,i=1,\ldots ,N\}$ are independent and identically distributed.

Note that the proofs of our theorems differ from those of Zhou et al. (2017b, 2018) in several aspects. First, our likelihood function is not exact, since an estimate of the covariate distribution rather than the true one is used. Thus, we have to deal with the difference between our approximate likelihood and the exact likelihood that assumes the covariate distribution to be known. For establishing consistency and rate of convergence, the proofs of our theorems follow the similar ideas as those in Zhou et al. (2017b, 2018), except that we need to additionally establish the closeness of the approximate and exact likelihoods. For establishing asymptotic normality and deriving the asymptotic covariance matrix, our approach is quite different from those in Zhou et al. (2017b, 2018), since we have to account for the additional variability induced by the estimated covariate distribution.

Before proving Theorems 1 & 2, we first define the class of functions $\mathcal {L}_N=\{l(\theta ,O): \theta \in \Theta _N\}$, where $l(\theta ,O)$ is the log-likelihood function based on a single observation O given by

$$\begin{aligned} \begin{aligned} l(\theta ,O)&\,=\, R\log f(Y|Z;\theta )+(1-R)\log f_Y(Y) \\&\,=\, R\log f(Y|Z;\theta )+(1-R)\log \int f(Y|z;\theta )dG_Z(z), \end{aligned} \end{aligned}$$

where the covariate distribution $G_Z(z)$ is assumed to be known and

$$\begin{aligned} f(Y|Z;\theta )=(1-S(U|Z))^{\Delta _{1}} (S(U|Z)-S(V|Z))^{\Delta _{2}} S(V|Z)^{1-\Delta _{1}-\Delta _{2}} \end{aligned}$$

with $S(t|Z)=\exp (-\Lambda (t)e^{\beta 'Z})$. Let $P_N$ denote the empirical measure. For any $\epsilon >0$, we define the covering number $N(\epsilon ,\mathcal {L}_N,L_1(P_N))$ as the smallest value of $\kappa$ for which there exists $\{\theta ^{(1)},\ldots ,\theta ^{(\kappa )}\}\in \Theta _N$ such that

$$\begin{aligned} \min _{j\in \{1,\cdots ,\kappa \}}\frac{1}{N}\sum _{i=1}^N\Big |l(\theta ,O_i) -l(\theta ^{(j)},O_i)\Big |<\epsilon \end{aligned}$$

for all $\theta \in \Theta _N$. If no such $\kappa$ exists, define $N(\epsilon ,{\mathcal {L}}_N,L_1(P_N))=\infty$.

Proof of Theorem 1

We now prove the strong consistency of $\hat{\theta }_N$. Based on Lemma 1 in the Supplementary Materials, the covering number of $\mathcal {L}_N$ satisfies

$$\begin{aligned} N\left( \epsilon ,\mathcal {L}_N,L_1(P_N)\right) \le KM_N^{(m+1)}\epsilon ^{-(p+m+1)} \, . \end{aligned}$$

Then by Lemma 2 in the Supplementary Materials, we have

$$\begin{aligned} \sup _{\theta \in \Theta _N} \big |P_Nl(\theta ,O)-Pl(\theta , O)\big |\rightarrow 0\quad \text {almost surely}. \end{aligned}$$

(A.1)

Furthermore, define

$$\begin{aligned} \begin{aligned} P_N \hat{l}(\theta ,O)&=\frac{1}{N}\sum _{i=1}^N \left\{ R_i\log f(Y_i|Z_i;\theta )+(1-R_i)\log \int f(Y_i|z;\theta )d\hat{G}_Z(z)\right\} \\&=\frac{1}{N}\sum _{i=1}^N \left[ R_i\log f(Y_i|Z_i;\theta )+(1-R_i)\right. \\&\qquad \left. \log \left\{ \sum _{k=1}^4 \frac{N_k}{N (n_k+n_{0k})} \sum _{r\in I_{v_k}} f(Y_i|Z_r;\theta ) \right\} \right] . \end{aligned} \end{aligned}$$

Then it is easy to show that

$$\begin{aligned} \sup _{\theta \in \Theta _N} \big |P_N\hat{l}(\theta ,O)-P_Nl(\theta , O)\big |\rightarrow 0\quad \text {almost surely}. \end{aligned}$$

(A.2)

Let $M(\theta , O)=-l(\theta , O)$ and $P_N\hat{M}(\theta , O)=-P_N\hat{l}(\theta , O)$. Define $K_\epsilon =\{\theta : d(\theta , \theta _0) \ge \epsilon , \theta \in \Theta _N\}$ for $\epsilon > 0$ and

$$\begin{aligned} \begin{aligned} \zeta _{1N}=&\sup _{\theta \in \Theta _N} |P_NM(\theta , O)-PM(\theta ,O)|,\\ \zeta _{2N}=&\sup _{\theta \in \Theta _N} |P_N\hat{M}(\theta , O)-P_NM(\theta ,O)|,\\ \zeta _{3N}=&P_N\hat{M}(\theta _0,O)-PM(\theta _0,O). \end{aligned} \end{aligned}$$

Then we obtain

$$\begin{aligned} \inf _{K_\epsilon }PM(\theta , O)\le \zeta _{1N}+\zeta _{2N}+\inf _{K_\epsilon }P_N\hat{M}(\theta , O). \end{aligned}$$

(A.3)

If $\hat{\theta }_N\in K_\epsilon ,$ we have

$$\begin{aligned} \inf _{K_\epsilon } P_N\hat{M}(\theta , O)=P_N\hat{M}(\hat{\theta }_N,O)\le P_N\hat{M}(\theta _0,O)=\zeta _{3N}+PM(\theta _0,O). \end{aligned}$$

(A.4)

Define $\delta _\epsilon =\inf _{K_\epsilon }P M(\theta , O)-PM(\theta _0,O)$. Then under Conditions (C1) - (C5), using the same arguments as those in Zhang et al. (2010, p. 352), we can prove $\delta _\epsilon >0$. It follows from (A.3) and (A.4) that

$$\begin{aligned} \inf _{K_\epsilon }PM(\theta , O)\le \zeta _{1N}+\zeta _{2N} + \zeta _{3N} +PM(\theta _0,O) = \zeta _N+ PM(\theta _0,O) \end{aligned}$$

with $\zeta _N=\zeta _{1N}+\zeta _{2N}+\zeta _{3N},$ and hence $\zeta _N \ge \delta _\epsilon .$ This gives $\{\hat{\theta }_N \in K_{\epsilon } \}\subseteq \{\zeta _N \ge \delta _{\epsilon }\}$, and by (A.1), (A.2) and the strong law of large numbers, we have $\zeta _{N}\rightarrow 0$ almost surely. Therefore, $\cup _{k=1}^{\infty }\cap _{N=k}^{\infty }\{\hat{\theta }_N \in K_{\epsilon } \} \subseteq \cup _{k=1}^{\infty }\cap _{N=k}^{\infty }\{\zeta _N \ge \delta _{\epsilon }\}$, which proves that $d(\hat{\theta }_N,\theta _0)\rightarrow 0$ almost surely.

Now we will derive the rate of convergence by using Theorem 3.4.1 of van der Vaart and Wellner (1996). Below let $\tilde{K}$ denote a universal positive constant that may differ from place to place. First note from Theorem 1.6.2 of Lorentz (1986) that there exists a Bernstein polynomial $\Lambda _{N0}$ such that $\Vert \Lambda _{N0}-\Lambda _{0}\Vert _{\infty } = O(m^{-r/2})=O(N^{-r\nu /2}).$ Define $\theta _{N0}=(\beta _0,\Lambda _{N0})$, then $d(\theta _{N0},\theta _0)=O(N^{-r\nu /2})$. For any $\eta >0,$ define the class of functions ${\mathcal {F}}_{\eta }=\{l(\theta ,O)-l(\theta _{N0},O): \theta \in \Theta _N,\, \eta /2 < d(\theta ,\theta _{N0})\le \eta \}.$ One can easily show that $P(l(\theta _0,O)-l(\theta _{N0},O))\le \tilde{K}d(\theta _0,\theta _{N0})\le \tilde{K}N^{-r\nu /2}.$ Also under Condition (C1)–(C5), using the same arguments as those in Zhang et al. (2010, p. 352), we obtain $P(l(\theta _0,O)-l(\theta ,O))\ge \tilde{K} d^2(\theta _0,\theta )$. Therefore, for large N, we have $P(l(\theta ,O)-l(\theta _{N0},O))=P(l(\theta ,O)-l(\theta _0,O))+P(l(\theta _0,O)-l(\theta _{N0},O))\le -\tilde{K}\eta ^2+\tilde{K}N^{-r \nu /2}=-\tilde{K}\eta ^2,$ for any $l(\theta ,O)-l(\theta _{N0},O)\in {\mathcal {F}}_{\eta }.$

Following the calculations in Shen and Wong (1994, p. 597), we have that for $0<\varepsilon <\eta$, $\log N_{[]}(\varepsilon ,{\mathcal {F}}_{\eta },L_2(P))\le \tilde{K} (m+1)\log (\eta /\varepsilon )$. Some algebraic manipulations give $P(l(\theta ,O)-l(\theta _{N0},O))^2\le \tilde{K} \eta ^2$ for any $l(\theta ,O)-l(\theta _{N0},O)\in {\mathcal {F}}_{\eta }.$ Also under Conditions (C1) - (C4), ${\mathcal {F}}_{\eta }$ is uniformly bounded. Then by Lemma 3.4.2 of van der Vaart and Wellner (1996), we obtain

$$\begin{aligned} E_P\Vert N^{1/2}(P_N-P)\Vert _{{\mathcal {F}}_{\eta }}\le \tilde{K}J_{[]}(\eta ,{\mathcal {F}}_{\eta },L_2(P)) \biggl \{1+\frac{J_{[]}(\eta ,{\mathcal {F}}_{\eta },L_2(P))}{\eta ^2N^{1/2}}\biggl \} \end{aligned}$$

with

$$\begin{aligned} J_{[]}(\eta ,{\mathcal {F}}_{\eta },L_2(P))=\int _0^\eta \Big \{1+\log N_{[]}(\varepsilon ,{\mathcal {F}}_{\eta },L_2(P))\Big \}^{1/2}d\varepsilon \le \tilde{K} (m+1)^{1/2}\eta . \end{aligned}$$

Then we have

$$\begin{aligned}&\sup _{\eta /2< d(\theta ,\theta _{N0})\le \eta ,\theta \in \Theta _N} N^{1/2}\left[ (P_N\hat{l}(\theta ,O)-Pl(\theta ,O))-(P_N\hat{l}(\theta _{N0},O) -Pl(\theta _{N0},O))\right] \\&\quad =\sup _{\eta /2 < d(\theta ,\theta _{N0})\le \eta ,\theta \in \Theta _N} N^{1/2}\Big [\big \{(P_N\hat{l}(\theta ,O)-P_Nl(\theta , O)) - (P_N\hat{l}(\theta _{N0},O)\\&\qquad -P_Nl(\theta _{N0}, O))\big \}\\&\qquad + \big \{(P_Nl(\theta ,O)-Pl(\theta ,O))-(P_Nl(\theta _{N0},O)-Pl(\theta _{N0},O))\big \}\Big ]\\&\quad \le 2N^{1/2}\sup _{\theta \in \Theta _N} \big |P_N\hat{l}(\theta ,O)-P_Nl(\theta , O)\big | + E_P\Vert N^{1/2}(P_N-P)\Vert _{{\mathcal {F}}_{\eta }}\\&\quad \le \tilde{K} \big \{(m+1)^{1/2}\eta +(m+1)N^{-1/2}\big \}. \end{aligned}$$

Define $\phi _N(\eta )=(m+1)^{1/2}\eta +(m+1)N^{-1/2}$. It is obvious that $\phi _N(\eta )/\eta$ is decreasing in $\eta$. Let $r_N=N^{min\{(1-\nu )/2,r\nu /2\}}$, then $r_N^2\phi _N(1/r_N)=r_N(N^\nu +1)^{1/2}+r_N^2(N^\nu +1)N^{-1/2}\le \tilde{K}N^{1/2}$.

Note that $d(\hat{\theta }_N,\theta _{N0})\le d(\hat{\theta }_N,\theta _0)+d(\theta _0,\theta _{N0})\rightarrow 0$ in probability. It then follows from Theorem 3.4.1 of van der Vaart and Wellner (1996) that $r_N d(\hat{\theta }_N,\theta _{N0})=O_p(1)$. Furthermore, by $d(\theta _{N0},\theta _0)=O(N^{-r\nu /2})$, we have $r_N d(\hat{\theta }_N,\theta _0)\le r_N d(\hat{\theta }_N,\theta _{N0}) + r_N d(\theta _{N0},\theta _0) = O_p(1)$ which completes the proof.$\square$

Proof of Theorem 2

We now sketch the proof of the asymptotic normality of $\hat{\beta }_N$. Let $l_\beta (\theta ,O)$ denote the score for $\beta$ given by

$$\begin{aligned} l_\beta (\theta ,O)\,=\, R\frac{f_\beta (Y|Z;\theta )}{f(Y|Z;\theta )}+(1-R)\frac{\int f_\beta (Y|z;\theta )dG_Z(z)}{\int f(Y|z;\theta )dG_Z(z)}, \end{aligned}$$

where

$$\begin{aligned} f_\beta (Y|Z;\theta )=(1-S_\beta (U|Z))^{\Delta _{1}} (S_\beta (U|Z)-S_\beta (V|Z))^{\Delta _{2}} S_\beta (V|Z)^{1-\Delta _{1}-\Delta _{2}} \end{aligned}$$

and

$$\begin{aligned} S_\beta (t|Z)=\exp (-\Lambda (t)e^{\beta 'Z})(-\Lambda (t)e^{\beta 'Z})Z. \end{aligned}$$

Consider a parametric smooth submodel with parameter $\theta _{(s)}=(\beta ,\Lambda _{(s)})$, where $\Lambda _{(0)}=\Lambda$ and

$$\begin{aligned} \left. \frac{\partial \Lambda _{(s)}}{\partial s}\right| _{s=0}=h. \end{aligned}$$

Let $\mathcal {H}\subseteq L_2(P)$ denote the class of functions h defined by this equation. The score operator for $\Lambda$ is

$$\begin{aligned} \begin{aligned} l_\Lambda (\theta ,O)[h]&\,=\,\left. \frac{\partial l(\theta _{(s)},O)}{\partial s}\right| _{s=0}\\&\,=\, R\frac{f_\Lambda (Y|Z;\theta )[h]}{f(Y|Z;\theta )}+(1-R)\frac{\int f_\Lambda (Y|z;\theta )[h]dG_Z(z)}{\int f(Y|z;\theta )dG_Z(z)}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} f_\Lambda (Y|Z;\theta )[h]= & {} (1-S_\Lambda (U|Z)[h])^{\Delta _{1}} (S_\Lambda (U|Z)[h]\\&-S_\Lambda (V|Z)[h])^{\Delta _{2}} S_\Lambda (V|Z)[h]^{1-\Delta _{1}-\Delta _{2}} \end{aligned}$$

and

$$\begin{aligned} S_\Lambda (t|Z)[h]=\exp (-\Lambda (t)e^{\beta 'Z})(-e^{\beta 'Z})h(t). \end{aligned}$$

According to Bickel et al. (1993), the efficient score for $\beta$ is

$$\begin{aligned} l^*(\theta ,O)\,=\,l_\beta (\theta ,O)-l_\Lambda (\theta ,O)[h_0], \end{aligned}$$

where $h_0\in \mathcal {H}^p$ minimizes $P\Vert l_\beta (\theta ,O)-l_\Lambda (\theta ,O)[h]\Vert ^2$ and is called the least favorable direction. Then the information for $\beta$ is

$$\begin{aligned} I(\beta )=P\big [l^*(\theta ,O)^{\otimes 2}\big ]=P\big [(l_\beta (\theta ,O)-l_\Lambda (\theta ,O)[h_0])^{\otimes 2}\big ], \end{aligned}$$

where $v^{\otimes 2} = v v'$ for a column vector $v\in R^p$. Under Conditions (C1)-(C5), the existence of the least favorable direction and the positive definiteness of the information can be similarly established as Theorem 4.1 in Huang and Wellner (1997).

Since $\hat{\theta }_N$ maximizes $P_N\hat{l}(\theta ,O)$ which is obtained by replacing $G_Z$ in $P_Nl(\theta ,O)$ with its consistent estimator $\hat{G}_Z$, $\hat{\theta }_N$ is the solution to the functional equation $P_N\hat{l}^*(\theta ,O)=0$, where $P_N\hat{l}^*(\theta ,O)$ is obtained by replacing $G_Z$ in $P_Nl^*(\theta ,O)$ with $\hat{G}_Z$. First note that $\hat{G}_Z$ is a $\sqrt{N}$-consistent estimator of $G_Z$. Similarly as the proofs of Theorem 2 in Zhang et al. (2010), one can establish that

$$\begin{aligned} N^{1/2} ( \hat{\beta }_N - \beta _0 ) = N^{1/2} I^{-1}(\beta _0) P_N\hat{l}^*(\theta _0,O)+o_p(1). \end{aligned}$$

Following the proofs of Theorem 2 in Weaver and Zhou (2005), one can further establish that

$$\begin{aligned} N^{1/2} ( \hat{\beta }_N - \beta _0 ) \rightarrow \, N ( 0 , \Sigma ) \end{aligned}$$

in distribution with the asymptotic covariance matrix given by

$$\begin{aligned} \Sigma =I^{-1}(\beta _0)+\sum _{l=1}^4 \frac{\pi _l^2}{\rho _l \rho _v + \pi _l \rho _0\rho _v}I^{-1}(\beta _0)\Sigma _l(\theta _0)I^{-1}(\beta _0). \end{aligned}$$

Here $I(\beta )$ is the information for $\beta$ defined above, and

$$\begin{aligned} \Sigma _l(\theta )=\mathrm{var}_{\{Z|Y\in A_l\}}\left\{ \sum _{k=1}^4 [\pi _k(1-\rho _0\rho _v)-\rho _k\rho _v] E_{\{Y|Y\in A_k\}}[M_Z(Y;\theta )]\right\} , \end{aligned}$$

where

$$\begin{aligned} M_Z(Y;\theta )=\frac{\partial f(Y|Z;\theta )/\partial \theta }{f_Y(Y;\theta )}-\frac{\partial f_Y(Y;\theta )/\partial \theta }{[f_Y(Y;\theta )]^2}f(Y|Z;\theta ), \end{aligned}$$

with

$$\begin{aligned} \frac{\partial f(Y|Z;\theta )}{\partial \theta }\equiv & {} f_\beta (Y|Z;\theta )-f_\Lambda (Y|Z;\theta )[h_0]\quad \text {and}\quad \frac{\partial f_Y(Y;\theta )}{\partial \theta } \\\equiv & {} \int \frac{\partial f(Y|z;\theta )}{\partial \theta } dG_Z(z). \end{aligned}$$

$\square$