1 Introduction

It has been known for several decades that periodic control strategies can improve the performance of nonlinear chemical reactions in comparison to their steady-state operations [5, 13, 18]. On the one hand, lumped parameter reaction models with harmonic inputs have been extensively studied in the literature with the use of frequency-domain methods (see, e.g., [6, 10] and references therein), On the other hand, it follows from the Pontryagin maximum principle that the optimal controls are bang-bang for the maximization of the average reaction product within the considered class of models [12, 18, 19]. An analytical design of periodic bang-bang controllers has been proposed in [2] for the isoperimetric optimization problem. The above optimal control techniques, developed for model systems or ordinary differential equations, are not directly applicable to infinite-dimensional reaction models.

An important class of distributed parameter control systems is represented by mathematical models of plug flow reactors (PFR) governed by hyperbolic systems of partial differential equations [1]. Even though there is a comprehensive engineering literature on PFR models (cf. [13] and references therein), the periodic optimal control problems require a rigorous analysis from the mathematical viewpoint. Just a few results, dealing with non-optimality of steady state solutions and comparison of different control strategies [7, 14] as well as the \(\varPi \)-test and properness condition [11], are available in this area.

In this paper, we will study the nonlinear hyperbolic control systems that describe chemical reactions of the type “\(A\rightarrow \) product” carried out in a PFR in the presence of an additional inert component (dilutant or solvent). The key contributions of our work are summarized below:

  • An analytic representation of the cost functional is derived for the PFR model in the cases of one- and two-dimensional inputs by using the method of characteristics;

  • Optimality conditions are obtained in the general class of measurable control functions;

  • The optimal controls are not unique, and a parameterization with one switching only can be used to achieve the optimality condition.

The rest of this paper is organized as follows. A single-input nonlinear control system will be considered in Sect. 2 as a PFR model with boundary injection. The isoperimetric optimal control problem will be solved for this model in order to maximize the conversion of the input reactant (A) into the product. An extension of these results to the PFR with time-varying flow-rate will be presented in Sect. 3. A comparative analysis of different control strategies will be performed in Sect. 4 under a specific choice of reaction parameters. Finally, Sect. 5 contains some concluding remarks.

2 Plug Flow Reactor Model

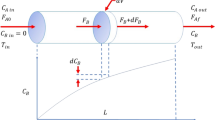
Consider an isothermal reaction of the type “\(A\rightarrow \) product” in a plug flow reactor (PFR) model [13, p. 394]:

$$\begin{aligned}{} & {} \frac{\partial C_A (x,t)}{\partial t}+v\frac{\partial C_A(x,t)}{\partial x}=-kC_A^n(x,t),\qquad (x,t)\in \varOmega =[0,L]\times \mathbb {R}, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} C_A(0,t)=C_{A_0}(t), \end{aligned}$$
(2)

where \(C_A(x,t)\) is the reactant A concentration inside the reactor at the distance x from the inlet and time t, L is the length of the reactor tube, \(C_{A_0}(t)\) is the concentration of A in the inlet stream that contains also another inert component, \(n>0\) is the reaction order, \(v>0\) is the flow-rate of the reaction stream, and \(k>0\) is the kinetic constant. The function \(C_{A_0}(t)\in [C_{\textrm{min}},C_{\textrm{max}}]\) is treated as the control input and assumed to be bounded by some constants \(C_{\textrm{max}}>C_{\textrm{min}}>0\).

The reaction order n is typically associated with the stoichiometric coefficient of a component in a specific reaction. For instance, for the reaction of the type “\(A + B \rightarrow \) product(s)”, the rate law is given by the formula \(r = k\cdot C_A^{n_1}\cdot C_B^{n_2}\) where \(n_1\) and \(n_2\) represent the orders concerning components A and B, respectively. The overall order of this reaction is \(n_1+n_2\). In our one-component model, the rate law \(-kC_A^n(x,t)\) appears on the right-hand side of (1), and the reaction order n typically does not deviate much from the stoichiometric coefficients and remains in the range (0, 2].

The boundary value problem (1), (2) can be solved by the method of characteristics [7]:

$$\begin{aligned} C_A(x,t)=\left( C_{A_0}\left( t-\frac{x}{v}\right) ^{-(n-1)}+\frac{k(n-1)}{v}x\right) ^{-\frac{1}{n-1}},\quad n\ne 1. \end{aligned}$$
(3)

For the case \(n=1\), the solution has the following form:

$$\begin{aligned} C_A(x,t)=C_{A_0}\left( t-\frac{x}{v}\right) e^{-\frac{k}{v}x}. \end{aligned}$$
(4)

If the function \(C_{A_0}(t)\) is continuously differentiable on \(\mathbb R\), then expressions (3)–(4) define the classical solution of the problem (1)–(2). It is easy to see that, in order to define C(x, s) for all \(x\in [0,L]\) at a given s, the information about \(C_{A_0}(t)\) on the closed interval \(t\in [s-\frac{L}{v},s]\) is needed. We are interested in studying an optimal control problem for system (1)–(2) with \(\tau \)-periodic controls \(C_{A_0}(t)\). In this case, it suffices to define the control \(C_{A_0}(t)\) on an interval \(t\in [0,\tau )\) and extend it to \(t\in \mathbb R\) by \(\tau \)-periodicity. For the subsequent formal analysis, we allow the functions \(C_{A_0}(t)\) to be discontinuous and introduce the class of admissible controls \(\mathcal{U}_\tau \) as follows.

Definition 2.1

Let \(\tau >0\), \(C_{\textrm{max}}>C_{\textrm{min}}>0\), and \(\overline{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\) be given. The class of admissible controls \(\mathcal {U}_{\,\tau }\) consists of all locally measurable functions \(C_{A_0}:\mathbb R\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\) such that \(C_{A_0}(t)\) is \(\tau \)-periodic and

$$\begin{aligned} \frac{1}{\tau }\int _0^\tau C_{A_0}(t)dt=\overline{C}. \end{aligned}$$
(5)

Formulas (3)–(4) correctly define the function \(C:\varOmega \rightarrow \mathbb R\) for any \(C_{A_0}\in \mathcal{U}_\tau \). We will refer to these functions C(x, t) as weak solutions of the problem (1)–(2) (see, e.g., [4]). Indeed, the above defined C(x, t) satisfies the integral identity

$$\begin{aligned} \int _\varOmega \left( C_A\frac{\partial \varphi }{\partial t}+vC_A\frac{\partial \varphi }{\partial x}+kC_A^n\varphi \right) dx\,dt=0, \end{aligned}$$
(6)

for each smooth test function \(\varphi \in C_0^\infty (\varOmega )\) with compact support.

Our goal is to optimize the conversion of A to the product by using time-varying inputs \(C_{A_0}(t)\) under the isoperimetric constraint (5) over a given period \(\tau \) as follows.

Problem 2.1

Given \(\tau >0\) and \(\overline{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\), find a control \(\hat{C}_{A_0}(\cdot )\in \mathcal {U}_{\,\tau }\) that minimizes the cost

$$\begin{aligned} J[C_{A_0}]=\frac{1}{\tau }\int _0^\tau C_A(L,t)\,v\,dt \end{aligned}$$
(7)

among all admissible controls \(C_{A_0}(\cdot )\in \mathcal {U}_{\,\tau }\). This cost function evaluates the mean molar flux of component A that leaves the reactor divided by the cross section area of the tube (in \([mol\,s^{-1}\,m^{-2}]\)). Here, the right-hand side of (7) contains the (weak) solution \(C_A(x,t)\) of the problem (1), (2) corresponding to the control \(C_{A_0}(t)\), so \(J[C_{A_0}]\) is well-defined in terms of \(C_{A_0}\) by formulas (3), (4).

In order to describe the optimal controls for Problem 2.1, we use the following notations. For a function \(u:[0,\tau )\rightarrow \mathbb R\), its \(\tau \)-periodic extension is denoted by \(u^\tau :\mathbb R \rightarrow \mathbb R\), so that \(u^\tau (t)\equiv u(t)\) for \(t\in [0,\tau )\), and the function \(u^\tau (t)\) is \(\tau \)-periodic. The Lebesgue measure of a set \(A\subset \mathbb R\) is denoted by \(\mu (A)\). Now we formulate the main result of this section.

Theorem 2.1

Let \(\tau >0\), \(C_{\textrm{max}}>C_{\textrm{min}}>0\), and \(\overline{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\) be given.

  1. 1)

    If \(n=1\), then all control functions \(C_{A_0}\in \mathcal {U}_{\,\tau }\) give the same value for the cost functional J.

  2. 2)

    If \(n<1\) and \(C_{\textrm{min}}>\left( \frac{v}{kL(1-n)}\right) ^{-\frac{1}{1-n}}\), then the steady-state control is optimal for Problem 2.1, namely

    $$\begin{aligned} C_{A_0}(t)=\overline{C} \qquad \text {for almost all }t\in [0,T]. \end{aligned}$$
    (8)
  3. 3)

    If \(n>1\), then the piecewise constant control \(C_{A_0}(t)=u^\tau (t)\) is optimal for Problem 2.1, where

    $$\begin{aligned} u(t)= {\left\{ \begin{array}{ll} C_{\textrm{min}}, &{}\text { if }\;t\in A^-, \\ C_{\textrm{max}}, &{}\text { if }\;t\in A^+=[0,\tau )\setminus A^-, \end{array}\right. } \end{aligned}$$
    (9)

    and \(A^-\subset [0,\tau )\) is any Lebesgue-measurable set such that

    $$\begin{aligned} \mu (A^-)=\frac{C_{\textrm{max}}-\overline{C}}{C_{\textrm{max}}-C_{\textrm{min}}}\tau . \end{aligned}$$

Remark 2.1

The optimal control problem 2.1 does not have a unique solution. The solution is always an equivalence class of functions defined by the value of (7).

The class of bang-bang controls (9) is an equivalence class of functions with different numbers of switchings between values \(C_{\textrm{max}}\) and \(C_{\textrm{min}}\). We note that the number of switchings does not impact the cost functional as the function \(\varPhi \) does not depend on time t explicitly. A simple representative of this class is \(C_{A_0}=c^\tau \in \mathcal{U}_\tau \) – the \(\tau \)-periodic extension of the control \(c:[0,\tau )\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\) with one switching of the following form:

$$\begin{aligned} c(t)= {\left\{ \begin{array}{ll} C_{\textrm{min}}, &{}\text { if }t\in [0,\tau ^*), \\ C_{\textrm{max}}, &{}\text { if }t\in [\tau ^*,\tau ), \end{array}\right. } \end{aligned}$$

where \(\tau ^*=\frac{C_{\textrm{max}}-\overline{C}}{C_{\textrm{max}}-C_{\textrm{min}}}\tau \).

Note that, as each admissible control \(C_{A_0}\in \mathcal{U}_\tau \) is periodic, the corresponding function \(C_A(x,t)\) in (3) and (4) is also \(\tau \)-periodic. For the case \(n\ne 1\), we modify the cost functional due to periodicity as follows:

$$\begin{aligned} J= & {} J[C_{A_0}]= \frac{v}{\tau }\int _0^\tau \left( C_{A_0}\left( t-Lv^{-1}\right) ^{-(n-1)}+\frac{kL(n-1)}{v}\right) ^{-\frac{1}{n-1}}dt \nonumber \\= & {} \frac{v}{\tau }\int _0^\tau \left( C_{A_0}(t)^{-(n-1)}+\frac{kL(n-1)}{v}\right) ^{-\frac{1}{n-1}}dt=:\frac{v}{\tau }\int _0^\tau \varPhi (C_{A_0}(t)) dt. \end{aligned}$$
(10)

It is easy to see that the function \(\varPhi \) is increasing and concave if \(n>1\). Indeed,

$$\begin{aligned}&\varPhi '(\xi )=\left[ 1+\frac{kL(n-1)}{v}\xi ^{n-1}\right] ^{-\frac{n}{n-1}}>0\;\text { if }n>1, \end{aligned}$$
(11)
$$\begin{aligned}&\varPhi ''(\xi )=-\frac{kL(n-1)n}{v}\left[ 1+\frac{kL(n-1)}{v}\xi ^{n-1}\right] ^{-\frac{2n-1}{n-1}}\xi ^{n-2}<0\;\text { if }n>1. \end{aligned}$$
(12)

To prove Theorem 2.1, we need to define a special class of control functions for Problem 2.1.

Definition 2.2

A function \(c:{\mathbb R}\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\) belongs to the class \(\mathcal {A}_{\,\widetilde{C}}\) for a given constant \(\widetilde{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\), if \(c(\cdot )\in \mathcal{U}_\tau \) and there exist Lebesgue-measurable sets \(A^+\subset [0,\tau )\), \(A^-\subset [0,\tau )\) such that:

  1. 1)

    \({{\,\mathrm{ess\,inf}\,}}_{t\in \mathbb {A}^+}c(t)\geqslant \widetilde{C}\);

  2. 2)

    \({{\,\mathrm{ess\,sup}\,}}_{t\in \mathbb {A}^-}c(t)\leqslant \widetilde{C}\);

  3. 3)

    \(\mu (A^+\cap A^-)=0\), \(\mu (A^+\cup A^-)=\tau \);

  4. 4)

    \(\mu (A^-)=\frac{C_{\textrm{max}}-\overline{C}}{C_{\textrm{max}}-C_{\textrm{min}}}\tau \).

In the paper [9], it was reported that the sinusoidal inputs ensure a better performance of the PFR reactor (with respect to the cost J) in comparison to the steady-state input \(C_{A_0}(t)\equiv \overline{C}\) if \(n>1\). We will show in the lemma below that the bang-bang strategies have even better performance than the sinusoidal ones. It is easy to see that \(\mathcal {A}_{\tilde{C}}\) contains the sinusoidal functions. For instance, assuming that \(\overline{C}-C_{\textrm{min}}=C_{\textrm{max}}-\overline{C}\), one can show that the function

$$\begin{aligned} C(t)=\overline{C}+(\overline{C}-C_{\textrm{min}})\sin \left( \frac{2\pi }{\tau }t\right) \end{aligned}$$

belongs to the class \(\mathcal {A}_{\,\overline{C}}\). Indeed, setting \(A^+=[0,\tau /2)\) and \(A^-=[\tau /2,\tau )\), we meet all the requirements of Definition 2.2.

Lemma 2.1

Let \(n>1\) and let \(C_\mathcal {A}(\cdot )\in \mathcal {A}_{\,\widetilde{C}}\) for some \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\). Then there exists a control \(C_b(\cdot )\in \mathcal{U}_\tau \) such that

$$\begin{aligned} J [C_b] \leqslant J [C_\mathcal {A}], \end{aligned}$$

where the cost J is defined in Problem 2.1.

Proof

Consider an arbitrary function \(C_\mathcal {A}(t)\) from the class \(\mathcal {A}_{\,\widetilde{C}}\) with a fixed \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\) and define now the corresponding bang-bang control \(c_b:[0,\tau )\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\):

$$\begin{aligned} c_{b}(t)= {\left\{ \begin{array}{ll} C_{\textrm{min}}, &{}\text { if }t\in A^-, \\ C_{\textrm{max}}, &{}\text { if }t\in A^+, \end{array}\right. } \end{aligned}$$
(13)

where the sets \(A^+\), \(A^-\) correspond to the class \(\mathcal {A}_{\widetilde{C}}\). Using condition 4) from Definition 2.2, we conclude that the isoperimetric condition (5) holds for the function \(C_b=c_b^\tau \) (the \(\tau \)-periodic extension of \(c_b\)), so \(C_b\in \mathcal {U}_{\,\tau }\).

Now using the isoperimetric condition (5) and the property of concave functions:

$$\begin{aligned} \varPhi (x)-\varPhi (y)\leqslant \varPhi '(y)(x-y)\quad \forall \,x,y\in [C_{\textrm{min}},C_{\textrm{max}}], \end{aligned}$$

we investigate the difference of costs \(J[C_b]-J[C_\mathcal {A}]\):

$$\begin{aligned} \begin{aligned}&J[C_b]-J[C_\mathcal {A}]=\frac{v}{\tau }\int _0^\tau \left( \varPhi (C_b(t))-\varPhi (C_\mathcal {A}(t))\right) dt \\ {}&\quad \leqslant \frac{v}{\tau }\int _0^\tau \varPhi '(C_\mathcal {A}(t))\left( C_b(t)-C_\mathcal {A}(t)\right) dt \\ {}&\quad =\frac{v}{\tau }\int _{A^+}\varPhi '(C_\mathcal {A}(t))\left( C_{\textrm{max}}-C_\mathcal {A}(t)\right) dt+\frac{v}{\tau }\int _{A^-}\varPhi '(C_\mathcal {A}(t))\left( C_{\textrm{min}}-C_\mathcal {A}(t)\right) dt \\ {}&\quad \leqslant \frac{v}{\tau }\int _{A^+}\varPhi '(\widetilde{C})\left( C_{\textrm{max}}-C_\mathcal {A}(t)\right) dt+\frac{v}{\tau }\int _{A^-}\varPhi '(\widetilde{C})\left( C_{\textrm{min}}-C_\mathcal {A}(t)\right) dt \\ {}&\quad =\frac{v}{\tau }\varPhi '(\widetilde{C})\int _0^\tau \left( C_{b}(t)-C_\mathcal {A}(t)\right) dt=0. \end{aligned} \end{aligned}$$

The obtained estimate proves Lemma 2.1. \(\square \)

Lemma 2.2

For any function \(u(\cdot )\in \mathcal {U}_{\,\tau }\), there exists a constant \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\) such that \(u(\cdot )\in \mathcal {A}_{\,\widetilde{C}}\).

Proof

Denote the values

$$\begin{aligned} \mu _{+}:=\frac{\overline{C}-C_{\textrm{min}}}{C_{\textrm{max}}-C_{\textrm{min}}}\tau , \qquad \mu _{-}:=\frac{C_{\textrm{max}}-\overline{C}}{C_{\textrm{max}}-C_{\textrm{min}}}\tau . \end{aligned}$$

It is clear that \(\mu _{+}+\mu _{-}=\tau \).

Assume that there exists a function \(u\in \mathcal {U}_{\,\tau }\) which does not belong to any class \(\mathcal {A}_{\,\widetilde{C}}\). Due to Definition 2.2, this means that, for any \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\), either

$$\begin{aligned} \mu (\{t\in [0,\tau ):u(t)>\widetilde{C}\})>\mu _{+}, \end{aligned}$$
(14)

or

$$\begin{aligned} \mu (\{t\in [0,\tau ):u(t)<\widetilde{C}\})>\mu _{-}. \end{aligned}$$
(15)

Consider the case (14) and rewrite this statement in the following way. For any arbitrary small \(\delta >0\), the following inequality always holds:

$$\begin{aligned} \mu (A^+_\delta )>\mu _{+},\text { where }A^+_\delta :=\{t\in [0,\tau ):u(t)\geqslant C_{\textrm{max}}-\delta \}. \end{aligned}$$
(16)

It is easy to prove that the only function which can satisfy the above statement is constant, namely, \(u(t)=C_{\textrm{max}}\) for \(\mu \)-a.a. \(t\in A^+_\delta \). Now we calculate the mean value of the function u:

$$\begin{aligned}&\frac{1}{\tau }\int _0^\tau u(t)\,dt=\frac{1}{\tau }\int _{A^+_\delta } u(t)\,dt+\frac{1}{\tau }\int _{[0,\tau )\setminus A^+_\delta } u(t)\,dt \\ {}&\quad \geqslant C_{\textrm{max}}\frac{|A^+_\delta |}{\tau }+C_{\textrm{min}}\frac{\tau -|A^+_\delta |}{\tau }=(C_{\textrm{max}}-C_{\textrm{min}})\frac{|A^+_\delta |}{\tau }+C_{\textrm{min}} \\ {}&\quad >(C_{\textrm{max}}-C_{\textrm{min}})\frac{\mu _{+}}{\tau }+C_{\textrm{min}}=\overline{C}. \end{aligned}$$

Thus we get that the isoperimetric constraint (5) is violated, so \(u\notin \mathcal {U}_{\,\tau }\), which contradicts our assumption.

Using the same arguments, one can prove that \(\frac{1}{\tau }\int _0^\tau u(t)\,dt<\overline{C}\) in the case (15). \(\square \)

Proof of Theorem 2.1

For the case \(n=1\), evaluating directly the value of the cost functional for solution (4), we get:

$$\begin{aligned} \begin{aligned} J&=\frac{v}{\tau }\int _0^\tau C_A(L,t)dt= \frac{v}{\tau }\int _0^\tau C_{A_0}\left( t-\frac{L}{v}\right) e^{-\frac{k}{v}L}dt \\ {}&=e^{-\frac{k}{v}L}\frac{v}{\tau }\int _0^\tau C_{A_0}(t)dt= \frac{v}{\tau }e^{-\frac{kL}{v}}\overline{C} \end{aligned} \end{aligned}$$

for any admissible \(\tau \)-periodic control function \(C_{A_0}(t)\).

In the case \(n<1\), it follows from (12) that \(\varPhi \) is a convex function, provided that \(C_{\textrm{min}}>\left( \frac{v}{kL(1-n)}\right) ^{-\frac{1}{1-n}}\). Using Jensen’s inequality for convex functions, we get

$$\begin{aligned} \varPhi (\overline{C})<\frac{1}{\tau }\int _0^\tau \varPhi (C_{A_0}(t)) dt \end{aligned}$$

for each non-negative Lebesgue-integrable function \(C_{A_0}\), which proves the second statement of the theorem.

For the case \(n>1\), we have the opposite Jensen’s inequality which means that any non-negative Lebesgue–integrable periodic function \(C_{A_0}\), which satisfied the constraints of Problem 2.1, ensures a better performance in the sense of the functional J in comparison with the steady-state control \(\overline{C}\) (see also [7]). Due to Lemmas 2.1, 2.2, the bang-bang strategy is the optimal control in terms of Problem 2.1. \(\square \)

3 Plug Flow Reactor Model Considering a Controlled Flow-rate

In this section, we investigate the mathematical model of PFR with a time-varying flow-rate v(t):

$$\begin{aligned}{} & {} \frac{\partial C_A}{\partial t}+v(t)\frac{\partial C_A}{\partial x}+kC_A^n=0,\qquad (x,t)\in \varOmega = [0,L]\times \mathbb {R}, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} C_A(0,t)=C_{A_0}(t). \end{aligned}$$
(18)

For this model, we are interested in the following optimal control problem:

Problem 3.1

Given positive constants \(\tau \), \(C_{\textrm{min}}<C_{\textrm{max}}\), \(v_{\textrm{min}}<v_{\textrm{max}}\), \(\overline{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\), and \(\overline{v}\in [v_{\textrm{min}},v_{\textrm{max}}]\), find \(\tau \)-periodic measurable controls \(\hat{C}_{A_0}:\mathbb {R}\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\) and \(\hat{v}:\mathbb {R}\rightarrow [v_{\textrm{min}},v_{\textrm{max}}]\) that minimize the cost

$$\begin{aligned} J=\frac{1}{\tau }\int _0^\tau C_A(L,t)\,v(t)\,dt \end{aligned}$$
(19)

among all solutions \(C_A(x,t)\) of the problem (17), (18) corresponding to the class of admissible controls, i.e. \(\tau \)-periodic measurable functions \(C_{A_0}:\mathbb R\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\) and \(v:\mathbb R\rightarrow [v_{\textrm{min}},v_{\textrm{max}}]\) that satisfy the isoperimetric constraint

$$\begin{aligned} \frac{1}{\tau }\int _0^\tau C_{A_0}(t)v(t)dt=\overline{C}\,\overline{v}. \end{aligned}$$
(20)

We will also consider the additional assumption:

$$\begin{aligned} \int _0^\tau v(t)dt=L, \end{aligned}$$
(21)

which means that the residence time of the reaction is equal to \(\tau \). To ensure the isoperimetric condition (20), we will assume that

$$\begin{aligned} C_{\textrm{min}}\leqslant \,\frac{\overline{C}\,\overline{v}\,\tau }{L}\leqslant C_{\textrm{max}}. \end{aligned}$$
(22)

We solve the problem (17), (18) using the method of characteristics. Namely, we write the Lagrange equations to find the characteristics curves:

$$\begin{aligned}&\frac{dt}{ds}=1,\quad t(0,r)=r, \end{aligned}$$
(23)
$$\begin{aligned}&\frac{dx}{ds}=v(t),\quad x(0,r)=0, \end{aligned}$$
(24)
$$\begin{aligned}&\frac{dz}{ds}=-kz^n,\quad z(0,r)=C_{A_0}(r). \end{aligned}$$
(25)

Here \(t=t(s,r)\), \(x=x(s,r)\) define the characteristic curve. Solving equations (23) and (24), we get:

$$\begin{aligned} \begin{aligned}&t(s,r)=s+r, \\ {}&x(s,r)=V(s+r)-V(r), \end{aligned} \end{aligned}$$

where the function V is defined by

$$\begin{aligned} V(t):=\int _0^tv(\xi )d\xi \end{aligned}$$

and is a strictly increasing function due to the positivity of v. Thus, we can express s and r in terms of x and t:

$$\begin{aligned} \begin{aligned}&s(x,t)=t-V^{-1}(V(t)-x), \\ {}&r(x,t)=V^{-1}(V(t)-x), \end{aligned} \end{aligned}$$

where the function \(V^{-1}\) denotes the inverse to V. Solving equation (25) in the case \(n\ne 1\), we get the solution of the problem (17), (18):

$$\begin{aligned} z(s,r)= & {} \left[ C_{A_0}(r)^{-(n-1)}+k(n-1)s\right] ^{-\frac{1}{n-1}}, \nonumber \\ C_A(x,t)= & {} \left[ C_{A_0}\left( V^{-1}(V(t)-x)\right) ^{-(n-1)}+k(n-1)\left( t-V^{-1}(V(t)-x)\right) \right] ^{-\frac{1}{n-1}}. \nonumber \\ \end{aligned}$$
(26)

For the case \(n=1\), the solution has the following form:

$$\begin{aligned}{} & {} z(s,r)=C_{A_0}(r)e^{-ks}, \nonumber \\{} & {} C_A(x,t)=C_{A_0}\left( V^{-1}(V(t)-x)\right) e^{-k\left( t-V^{-1}(V(t)-x)\right) }. \end{aligned}$$
(27)

Similarly to the previous study in Sect. 2, we consider the obtained solutions as weak solutions of the problem (17), (18) from the class of measurable functions in the sense of the integral identity:

$$\begin{aligned} \int _\varOmega \left( C_A\frac{\partial \varphi }{\partial t}+vC_A\frac{\partial \varphi }{\partial x}+kC_A^n\varphi \right) dx\,dt=0, \end{aligned}$$

for each smooth test function \(\varphi \in C_0^\infty (\varOmega )\) with compact support.

As we got the explicit solution of the problem (17), (18), we can study the structure of the cost functional (19). In order to do this, we introduce the class of admissible control functions and the following two auxiliary lemmas.

Definition 3.1

Let \(\tau >0\), \(C_{\textrm{max}}>C_{\textrm{min}}>0\), \(v_{\textrm{max}}>v_{\textrm{min}}>0\), \(L\in [v_{\textrm{min}}\tau ,v_{\textrm{max}}\tau ]\) and \(\overline{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\), \(\overline{v}\in [v_{\textrm{min}},v_{\textrm{max}}]\) be given. The class of admissible controls \(\mathcal {V}_{\,\tau }\) consists of all locally measurable vector-functions \((c,v):\mathbb R\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\times [v_{\textrm{min}},v_{\textrm{max}}]\) such that (c(t), v(t)) is \(\tau \)-periodic and the isoperimetric conditions (20), (21) hold.

Lemma 3.1

If the functions \((C_{A_0},v)\in \mathcal {V}_\tau \), then the corresponding solution C(x, t) of the problem (17), (18) is also \(\tau \)-periodic with respect to t.

Proof

Since v is a \(\tau \)-periodic function, we get for any \(s\in [0,\tau ]\):

$$\begin{aligned} V(\tau )=\int _0^\tau v(\xi )d\xi =\int _{-s}^{\tau -s}v(\xi )d\xi =-V(-s)+V(\tau -s). \end{aligned}$$

Under assumption (21) and the monotonicity of V, for each \(x\in [0,L]\) one can find an \(s\in [0,\tau ]\) such that \(x=-V(-s)\). Using this fact and the \(\tau \)–periodicity of the functions \(C_{A_0}\) and v, we get:

$$\begin{aligned} C_A(x,\tau )&=\left[ C_{A_0}\left( V^{-1}(V(\tau )-x)\right) ^{-(n-1)}+k(n-1)\left( \tau -V^{-1}(V(\tau )-x)\right) \right] ^{-\frac{1}{n-1}} \\ {}&=\left[ C_{A_0}\left( V^{-1}(V(\tau -s))\right) ^{-(n-1)}+k(n-1)\left( \tau -V^{-1}(V(\tau -s))\right) \right] ^{-\frac{1}{n-1}} \\ {}&=\left[ C_{A_0}(\tau -s)^{-(n-1)}+k(n-1)s\right] ^{-\frac{1}{n-1}} \\ {}&=\left[ C_{A_0}\left( -V^{-1}(-x)\right) ^{-(n-1)}+k(n-1)\left( -V^{-1}(-x)\right) \right] ^{-\frac{1}{n-1}} \\ {}&=C_A(x,0). \end{aligned}$$

\(\square \)

Lemma 3.2

Let the control functions \((C_{A_0},v)\in \mathcal {V}_\tau \) then the cost functional (19) of Problem 3.1 can be rewritten as follows:

$$\begin{aligned}&J[C_{A_0},v]=\frac{1}{\tau }\int _0^\tau C_{A_0}(t)e^{-k\tau }v(t)dt,\quad \text {if } n=1, \end{aligned}$$
(28)
$$\begin{aligned}&J[C_{A_0},v]=\frac{1}{\tau }\int _0^\tau \varPsi (C_{A_0}(t))v(t)dt,\quad \text {if } n\ne 1, \end{aligned}$$
(29)

where \(\varPsi (\xi ):=\left( \xi ^{-(n-1)}+k(n-1)\tau \right) ^{-\frac{1}{n-1}}\) is an increasing concave function in the case \(n>1\).

Proof

Using assumption (21), the \(\tau \)–periodicity of the function v and the definition of function V(t), we get

$$\begin{aligned} V^{-1}(V(t)-L)=V^{-1}(V(t)-V(\tau ))=V^{-1}(V(t-\tau ))=t-\tau , \end{aligned}$$

which allows us to rewrite the cost functional (19) in the case \(n\ne 1\) as follows:

$$\begin{aligned} \begin{aligned} J[C_{A_0},v]&=\frac{1}{\tau }\int _0^\tau \left[ C_{A_0}\left( t-\tau \right) ^{-(n-1)}+k(n-1)\left( t-(t-\tau ))\right) \right] ^{-\frac{1}{n-1}}v(t)dt \\ {}&=\frac{1}{\tau }\int _0^\tau \left[ C_{A_0}(t)^{-(n-1)}+k(n-1)\tau \right] ^{-\frac{1}{n-1}}v(t)dt, \end{aligned} \end{aligned}$$

provided that the function \(C_{A_0}\) is \(\tau \)–periodic. Calculating the derivatives of the function \(\varPsi \) as it was done in (11), (12), we conclude that, if \(n>1\), \(\varPsi \) is increasing and concave.

Similarly, under the conditions of Lemma 3.2, we obtain (28) in the case \(n=1\). \(\square \)

In solving the optimal control problem 3.1, we need the following definition of the class of bang-bang controls.

Definition 3.2

The class \(\mathcal {B}_{\tau }^0\) with given \(\tau >0\) is a class of control vector-functions \((c,v)\in \mathcal {V}_{\,\tau }\) which define the bang-bang strategy with respect to the constraints of Problem 3.1. Namely, the function v has the following form:

$$\begin{aligned} v(t)= {\left\{ \begin{array}{ll} v_{\textrm{min}}, &{}\text { if }t\in B^-, \\ v_{\textrm{max}}, &{}\text { if }t\in B^+,\text { for } t\in [0,\tau ), \end{array}\right. } \end{aligned}$$
(30)

where \(B^-,B^+\subset [0,\tau )\), \(\mu (B^+\cap B^-)=0\), \(\mu (B^+\cup B^-)=\tau \), and \(\mu (B^+)=\mu _v^+:=\frac{L-\tau v_{\textrm{min}}}{v_{\textrm{max}}-v_{\textrm{min}}}\), \(\mu (B^-)=\mu _v^-:=\frac{\tau v_{\textrm{max}}-L}{v_{\textrm{max}}-v_{\textrm{min}}}\) are defined by assumption (21). Moreover, function c is defined by the relation:

$$\begin{aligned} c(t)= {\left\{ \begin{array}{ll} C_{\textrm{max}}, &{}\text { if }t\in A^+, \\ C_{\textrm{min}}, &{}\text { if }t\in A^-, \end{array}\right. } \end{aligned}$$
(31)

where the sets \(A^+,A^-\subset [0,\tau )\) are defined to satisfy the isoperimetric constraint (20), and \(\mu (A^+\cap A^-)=0\), \(\mu (A^+\cup A^-)=\tau \).

We also need to define a class of controls \(\mathcal {B}_{\tau }\), which are optimal in \(\mathcal {B}_{\tau }^0\).

Definition 3.3

The class \(\mathcal {B}_{\tau }\) with given \(\tau >0\) is a class of control vector-functions \((\hat{c},\hat{v})\in \mathcal {B}_{\tau }^0\) which are defined by the following condition:

$$\begin{aligned} J[\hat{c},\hat{v}]=\min \limits _{(c,v)\in \mathcal {B}_{\tau }^0}J[c,v]. \end{aligned}$$

In order to investigate class \(\mathcal {B}_{\tau }\), we introduce the following lemma.

Lemma 3.3

For every element \((\hat{c},\hat{v})\in \mathcal {B}_{\tau }\) defined by the sets \(\hat{A}^{\pm }\), \(\hat{B}^{\pm }\), the following condition holds:

$$\begin{aligned} \mu (\hat{A}^+\cap \hat{B}^-)=\max \limits _{(c,v)\in \mathcal {B}_{\tau }^0}\mu (A^+\cap B^-), \end{aligned}$$
(32)

where the sets \({A}^{\pm }\), \({B}^{\pm }\) define the corresponding element \((c,v)\in \mathcal {B}_{\tau }^0\) according to (30), (31).

Proof

First, we construct the functions \(\hat{c}\), \(\hat{v}\) to satisfy condition (32). While the measures of the sets \(\hat{B}^{\pm }\) are defined by assumption (21) (see Definition 3.2), the expression of the measure of sets \(\hat{A}^\pm \) depends on the relation between the parameters of the problem. Assuming that condition (32) is satisfied, we have two possible cases:

  1. (i)

    If

    $$\begin{aligned} \kappa :=&\,\tau v_{\textrm{max}}(\overline{C}\overline{v}-C_{\textrm{max}}v_{\textrm{min}})+\tau v_{\textrm{min}}(C_{\textrm{min}}v_{\textrm{max}}-\overline{C}\overline{v})\\ {}&+L(C_{\textrm{max}}v_{\textrm{min}}-C_{\textrm{min}}v_{\textrm{max}})\leqslant 0, \end{aligned}$$

    then \(\mu (A^+)\leqslant \mu (B^-)\) and \(A^+\cap B^+=\emptyset \) (see Fig. 1a). In this case, the measures of sets \(A^\pm \) are as follows:

    $$\begin{aligned} \mu (A^+)=\mu _c^+:=\frac{\tau \overline{C}\overline{v}-LC_{\textrm{min}}}{v_{\textrm{min}}(C_{\textrm{max}}-C_{\textrm{min}})}, \qquad \mu (A^-)=\mu _c^-:=\tau -\mu _c^+. \end{aligned}$$
    (33)
  2. (ii)

    If \(\kappa >0\) then \(\mu (A^-)\le \mu (B^+)\) and \(A^-\cap B^-=\emptyset \) (see Fig. 1b). In this case, the measures of sets \(A^\pm \) are as follows:

    $$\begin{aligned} \mu (A^-)=\mu _c^-:=\frac{LC_{\textrm{max}}-\tau \overline{C}\overline{v}}{v_{\textrm{max}}(C_{\textrm{max}}-C_{\textrm{min}})}\qquad \mu (A^+)=\mu _c^+:=\tau -\mu _c^-. \end{aligned}$$
    (34)

Now we compare the cost functional on the constructed functions \(\hat{c}\), \(\hat{v}\) with the cost functional on the arbitrary functions \((c,v)\in \mathcal {B}_{\tau }^0\). In the case (i), we have:

$$\begin{aligned} \begin{aligned} \tau \left( J[c,v]-J[\hat{c},\hat{v}]\right) =&\varPsi (C_{\textrm{max}})v_{\textrm{max}}\,\mu (A^+ \cap B^+) +\varPsi (C_{\textrm{max}})v_{\textrm{min}}\,\mu (A^+ \cap B^-) \\ {}&+\varPsi (C_{\textrm{min}})v_{\textrm{max}}\,\mu (A^- \cap B^+) +\varPsi (C_{\textrm{min}})v_{\textrm{min}}\,\mu (A^- \cap B^-) \\ {}&-\varPsi (C_{\textrm{min}})v_{\textrm{max}}\,\mu (\hat{B}^+) -\varPsi (C_{\textrm{min}})v_{\textrm{min}}\,\mu (\hat{A}^- \cap \hat{B}^-) \\ {}&-\varPsi (C_{\textrm{max}})v_{\textrm{min}}\,\mu (\hat{A}^+) \end{aligned} \end{aligned}$$
Fig. 1
figure 1

Illustration of possible cases described for the class \(\mathcal {B}_{\tau }\)

Full size image

Since \(\mu (\hat{B}^+)=\mu ({B}^+)\), \(\mu (\hat{A}^+)=\mu ({A}^+)\), and \(\mu (\hat{A}^- \cap \hat{B}^-)=\mu (B^-)-\mu (A^+)\), and also, since for each set A we can state that \(\mu (A)=\mu (A\cap B^+)+\mu (A\cap B^-)\), we get after simple computations:

$$\begin{aligned} J[c,v]-J[\hat{c},\hat{v}]= \frac{1}{\tau }[\varPsi (C_{\textrm{max}})-\varPsi (C_{\textrm{min}})][v_{\textrm{max}}-v_{\textrm{min}}]\mu (A^+ \cap B^+)\geqslant 0. \end{aligned}$$

\(\square \)

Note that all admissible controls from the class \(\mathcal {B}_\tau \) are equivalent in the sense of Problem 3.1, namely, the functional J takes the same value for all controls \((c,v)\in \mathcal {B}_\tau \).

Moreover, the Problem 3.1 does not have a unique solution. The solution will be an equivalence class of functions in terms of the value of functional (19).

The result of solving the isoperimetric optimal control problem (Problem 3.1) is presented in the following theorem.

Theorem 3.1

Let assumptions (21) and (22) be satisfied.

  1. 1)

    If \(n=1\), then controls \(C_{A_0}\) and v have no impact on the value of the cost functional J, namely,

    $$\begin{aligned} J[C_{A_0},v]=\overline{C}\,\overline{v}e^{-k\tau }\qquad \forall \,(C_{A_0},v)\in \mathcal {V}_\tau . \end{aligned}$$
  2. 2)

    If \(n>1\), then the class of controls \(\mathcal {B}_\tau \) is the optimal strategy for Problem 3.1.

For further analysis, we introduce an auxiliary class of control functions.

Definition 3.4

A vector-function \((c,v):{\mathbb R}\rightarrow [C_{\textrm{min}},C_{\textrm{max}}]\times [v_{\textrm{min}},v_{\textrm{max}}]\) belongs to the class \(\mathcal {A}_{\,\widetilde{C},\,\nu }\) for given constants \(\widetilde{C}\in [C_{\textrm{min}},C_{\textrm{max}}]\), \(\nu \in [0,\tau ]\) if \((c,v)\in \mathcal{V}_\tau \) and there exist Lebesgue-measurable sets \(A^+\subset [0,\tau )\), \(A^-\subset [0,\tau )\) such that:

  1. 1)

    \({{\,\mathrm{ess\,inf}\,}}_{t\in \mathbb {A}^+}c(t)\geqslant \widetilde{C}\);

  2. 2)

    \({{\,\mathrm{ess\,sup}\,}}_{t\in \mathbb {A}^-}c(t)\leqslant \widetilde{C}\);

  3. 3)

    \(\mu (A^+\cap A^-)=0\), \(\mu (A^+\cup A^-)=\tau \);

  4. 4)

    \(\mu (A^+)=\nu \).

To prove Theorem 3.1, we need two auxiliary lemmas.

Lemma 3.4

Let \(n>1\) and let \((C_\mathcal {A},v)\in \mathcal {A}_{\,\widetilde{C},\,\mu _c^+}\) for some \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\), with \(\mu _c^+\) from Definition 3.3. Then there exist control functions \((C_b,v_b)\in \mathcal{B}_\tau \) such that

$$\begin{aligned} J [C_b,v_b] \leqslant J [C_\mathcal {A},v] \end{aligned}$$

where the cost J is defined in Problem 3.1.

Proof

Consider an arbitrary vector-function \((C_\mathcal {A}(t),v(t))\) from the class \(\mathcal {A}_{\,\widetilde{C},\,\mu _c^+}\) with a fixed \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\) and \(\mu _c^+\) defined in Definition 3.3. Define now the corresponding bang-bang control \(c_b:[0,\tau )\rightarrow [C_{\textrm{min}}],C_{\textrm{max}}]\):

$$\begin{aligned} c_{b}(t)= {\left\{ \begin{array}{ll} C_{\textrm{min}}, &{}\text { if }t\in A^-, \\ C_{\textrm{max}}, &{}\text { if }t\in A^+, \end{array}\right. } \end{aligned}$$
(35)

where the sets \(A^+\), \(A^-\) correspond to the class \(\mathcal {A}_{\,\widetilde{C},\,\mu _c^+}\). Set \(C_b=c_b^\tau \), the \(\tau \)-periodic extension of \(c_b\). Due to Definition 3.4, \(\mu (A^+)=\mu _c^+\) and \(\mu (A^-)=\mu _c^-\), so a control function \(v_b\) can be constructed, so that \((C_b,v_b)\in \mathcal {B}_\tau \).

Now using the isoperimetric conditions (20), (21) and the concavity property of the function \(\varPsi \):

$$\begin{aligned} \varPsi (x)-\varPsi (y)\leqslant \varPsi '(y)(x-y)\quad \forall \,x,y\in [C_{\textrm{min}},C_{\textrm{max}}], \end{aligned}$$

we investigate the difference of costs \(J[C_b,v_b]-J[C_\mathcal {A},v]\):

$$\begin{aligned} \begin{aligned}&J[C_b,v_b]-J[C_\mathcal {A},v]=\frac{1}{\tau }\int _0^\tau \left( \varPsi (C_b(t))v_b(t)-\varPsi (C_\mathcal {A}(t))v(t)\right) dt \\ {}&\quad =\frac{1}{\tau }\int _0^\tau \varPsi (C_b(t))(v_b(t)-v(t))dt +\frac{1}{\tau }\int _0^\tau \left( \varPsi (C_b(t))-\varPsi (C_\mathcal {A}(t))\right) v(t)dt \\ {}&\quad =:I_1+I_2 \end{aligned} \end{aligned}$$

Now we estimate the integral \(I_1\) in cases (i) and (ii) (see the proof of Lemma 3.3) separately. In case (i), due to assumption (21), we have:

$$\begin{aligned} \begin{aligned} I_1=&\frac{1}{\tau }\int _0^\tau \varPsi (C_b(t))(v_b(t)-v(t))dt =\frac{1}{\tau }\int _{A^+} \varPsi (C_{\textrm{max}})(v_{\textrm{min}}-v(t))dt \\ {}&+\frac{1}{\tau }\int _{A^-\cap B^-} \varPsi (C_{\textrm{min}})(v_{\textrm{min}}-v(t))dt+ \frac{1}{\tau }\int _{B^+} \varPsi (C_{\textrm{min}})(v_{\textrm{max}}-v(t))dt \\\leqslant&\frac{1}{\tau }\int _0^\tau \varPsi (C_{\textrm{min}})(v_b(t)-v(t))dt=0 \end{aligned} \end{aligned}$$

In case (ii), by similar logic, we have:

$$\begin{aligned} \begin{aligned} I_1=&\frac{1}{\tau }\int _0^\tau \varPsi (C_b(t))(v_b(t)-v(t))dt =\frac{1}{\tau }\int _{A^+} \varPsi (C_{\textrm{max}})(v_{\textrm{min}}-v(t))dt \\ {}&+\frac{1}{\tau }\int _{A^+\cap B^+} \varPsi (C_{\textrm{max}})(v_{\textrm{max}}-v(t))dt+ \frac{1}{\tau }\int _{B^+} \varPsi (C_{\textrm{min}})(v_{\textrm{max}}-v(t))dt \\\leqslant&\frac{1}{\tau }\int _0^\tau \varPsi (C_{\textrm{max}})(v_b(t)-v(t))dt=0 \end{aligned} \end{aligned}$$

The integral \(I_2\) can be estimated similarly as in the proof of Lemma 2.1:

$$\begin{aligned} \begin{aligned} I_2&=\frac{1}{\tau }\int _0^\tau \left( \varPsi (C_b(t))-\varPsi (C_\mathcal {A}(t))\right) v(t)dt \\ {}&\leqslant \frac{1}{\tau }\int _0^\tau \varPsi '(C_\mathcal {A}(t))\left( C_b(t)-C_\mathcal {A}(t)\right) v(t)dt \\ {}&\leqslant \frac{1}{\tau }\varPsi '(\widetilde{C})\int _0^\tau \left( C_{b}(t)-C_\mathcal {A}(t)\right) v(t)dt=0. \end{aligned} \end{aligned}$$

The obtained estimates prove Lemma 3.4. \(\square \)

Lemma 3.5

For any vector-function \((u(\cdot ),v(\cdot ))\in \mathcal {V}_{\,\tau }\), there exists a constant \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\) such that \((u(\cdot ),v(\cdot ))\in \mathcal {A}_{\,\widetilde{C},\mu _c^+}\), where \(\mu _c^+\) is from Definition 3.3.

Proof

Assume that there exists a vector-function \((u,v)\in \mathcal {U}_{\,\tau }\) which does not belong to any class \(\mathcal {A}_{\,\widetilde{C},\mu _c^+}\). Due to Definition 3.4, this means that, for any \(\widetilde{C}\in (C_{\textrm{min}},C_{\textrm{max}})\), either

$$\begin{aligned} \mu (\{t\in [0,\tau ):u(t)>\widetilde{C}\})>\mu _c^+, \end{aligned}$$
(36)

or

$$\begin{aligned} \mu (\{t\in [0,\tau ):u(t)<\widetilde{C}\})>\mu _c^-. \end{aligned}$$
(37)

By the same logic as in Lemma 2.2, we obtain that \(u(t)=C_{\textrm{max}}\) for \(\mu \)-a.a. \(t\in A^+_\delta \) in the case (36). Now we check if the isoperimetric constraint (20) holds. We will consider two cases (i) and (ii) introduced in the proof of Lemma 3.3. In case (i), we have:

$$\begin{aligned} \frac{1}{\tau }\int _0^\tau u(t)v(t)\,dt&=\frac{1}{\tau }\int _{A^+_\delta } C_{\textrm{max}}v(t)\,dt+\frac{1}{\tau }\int _{[0,\tau )\setminus A^+_\delta } u(t)v(t)\,dt \\ {}&\geqslant \frac{1}{\tau }\int _{A^+_\delta } C_{\textrm{max}}v(t)\,dt+\frac{1}{\tau }\int _{[0,\tau )\setminus A^+_\delta } C_{\textrm{min}}v(t)\,dt \\ {}&\geqslant \frac{1}{\tau }\int _{A^+_\delta } (C_{\textrm{max}}-C_{\textrm{min}})v_{\textrm{min}}\,dt+\frac{1}{\tau }C_{\textrm{min}}L \\ {}&>\frac{1}{\tau }\mu _c^+ (C_{\textrm{max}}-C_{\textrm{min}})v_{\textrm{min}}+\frac{1}{\tau }C_{\textrm{min}}L =\overline{C}\overline{v}. \end{aligned}$$

In case (ii), we have:

$$\begin{aligned} \frac{1}{\tau }\int _0^\tau u(t)v(t)\,dt&=\frac{1}{\tau }\int _{A^+_\delta } C_{\textrm{max}}v(t)\,dt+\frac{1}{\tau }\int _{[0,\tau )\setminus A^+_\delta } u(t)v(t)\,dt \\ {}&\geqslant \frac{1}{\tau }\int _{A^+_\delta } C_{\textrm{max}}v(t)\,dt+\frac{1}{\tau }\int _{[0,\tau )\setminus A^+_\delta } C_{\textrm{min}}v(t)\,dt \\ {}&\geqslant \frac{1}{\tau }C_{\textrm{max}}L- \frac{1}{\tau }\int _{[0,\tau )\setminus A^+_\delta } (C_{\textrm{max}}-C_{\textrm{min}})v_{\textrm{max}}\,dt \\ {}&>\frac{1}{\tau }C_{\textrm{max}}L-\frac{1}{\tau }\mu _c^-(C_{\textrm{max}}-C_{\textrm{min}})v_{\textrm{max}} =\overline{C}\,\overline{v}. \end{aligned}$$

Thus we get that the isoperimetric constraint (20) is violated in both cases, so \((u,v)\notin \mathcal {V}_{\,\tau }\), which contradicts our assumption.

Using the same arguments, one can prove that \(\frac{1}{\tau }\int _0^\tau u(t)v(t)\,dt<\overline{C}\,\overline{v}\) in the case (37). \(\square \)

Proof of Theorem 3.1

To solve Problem 3.1 under assumptions (21), (22) in the case \(n=1\), we minimize the cost functional (28) because of Lemma 3.2. Computing the cost value directly, we obtain

$$\begin{aligned} J[C_{A_0},v]=\frac{1}{\tau }\int _0^\tau C_{A_0}(t)e^{-k\tau }v(t)dt=\overline{C}\,\overline{v}e^{-k\tau }, \end{aligned}$$

which proves the first assertion of the theorem.

For the case \(n>1\), due to Lemmas 3.1, 3.2, 3.4, 3.5, we conclude that the control functions from \(\mathcal {B}_\tau \) have the best performance in terms of Problem 3.1, so the bang-bang strategy is optimal. \(\square \)

Remark 3.1

Considering the proposed bang-bang control strategy, we note that the number of switchings of v(t) and \(C_{A_0}(t)\) is not crucial due to the fact that the integrand in (29) does not depend on t explicitly. So, from the theoretical viewpoint, the switching frequency can be chosen in an arbitrary way that preserves the established measures of \(A^\pm \) and \(B^\pm \). However, it may not be desirable to switch too often from a practical point of view. Thus, the simplest optimal control strategy is parameterized by the sets \(A^\pm \) and \(B^\pm \) in the form of intervals, so that each control C(t) and v(t) has one switching per period \(\tau \) as depicted in Fig. 1.

4 Case Study

4.1 Comparison of Different Control Strategies

In this section, we consider the system (1), (2) under the following choice of model parameters (cf. [9]):

$$\begin{aligned} {\overline{C}}= & {} 1\ mol\,m^{-3}; \qquad n=2; \qquad k=0.001\ s^{-1}mol^{-1}; \nonumber \\ C_{\textrm{max}}= & {} 1.5\ mol\,m^{-3}; \qquad L=1\ m; \qquad \overline{v}=0.01\ m\,s^{-1}; \nonumber \\ C_{\textrm{min}}= & {} 0.5\ mol\,m^{-3}; \qquad \tau =100\ s. \end{aligned}$$
(38)

First, we consider the model (1), (2) with the controlled inlet concentration \(C_{A_0}\) and assume the constant flow-rate \(v=\overline{v}\). We define the sinusoidal function

$$\begin{aligned} C_{sin}(t)=\overline{C}+(\overline{C}-C_{\textrm{min}})\sin \left( \frac{2\pi }{\tau }t\right) = 1+0.5\sin \frac{\pi t}{50} \end{aligned}$$

and compare it with the bang-bang control function \(C_b(t)\):

$$\begin{aligned} C_b(t)= {\left\{ \begin{array}{ll} 1.5, &{}\text { if }t\in [0,50), \\ 0.5, &{}\text { if }t\in [50,100), \end{array}\right. } \text { and } \; C_b(t+100) = C_b(t) \; \text{ for } \text{ all } \; t\in {\mathbb R}. \end{aligned}$$

Now we compute directly the cost functional for both functions:

$$\begin{aligned} \begin{aligned} J[C_{sin}]&=\frac{1}{\tau }\int _0^\tau \varPhi (C_{sin}(t))\,v\, dt= 10^{-4}\int _0^{100}\frac{10\,C_1(t)}{10+C_1(t)}dt \\ {}&= 10^{-4}\int _0^{100}\frac{10+5\sin \left( \frac{\pi t}{50}\right) }{11+0.5\sin \left( \frac{\pi t}{50}\right) }dt \\ {}&\approx 8.9968\cdot 10^{-3} \left( \frac{mol}{m^2\,s}\right) , \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} J[C_b]&=\frac{v}{\tau }\int _0^\tau \varPhi (C_b(t)) dt \\ {}&= 10^{-4}\int _0^{50}\frac{10\,C_{\textrm{max}}}{10+C_{\textrm{max}}}dt+ 10^{-4}\int _{50}^{100}\frac{10\,C_{\textrm{min}}}{10+C_{\textrm{min}}}dt\\ {}&\approx 8.9027\cdot 10^{-3} \left( \frac{mol}{m^2\,s}\right) . \end{aligned} \end{aligned}$$

So, the difference between these costs is approximately \(9.416\cdot 10^{-5}\,{mol}\,{m^{-2}s^{-1}}\), which illustrates that the bang-bang strategy has more A consumed and thus the performance is about \(1.05\,\%\) better than for the sinusoidal one.

Calculating for comparison the cost function for the conventional steady-state operation

$$\begin{aligned} J[\overline{C}]=\frac{1}{\tau }\int _0^\tau \varPhi (\overline{C})\,v\, dt= 10^{-2}\int _0^{100}\frac{10\,\overline{C}}{10+\overline{C}}\,dt\approx 9.0909\cdot 10^{-3} \left( \frac{mol}{m^2\,s}\right) , \end{aligned}$$

we see that the bang-bang strategy is \(2.07\,\%\) better than the steady-state control.

Now we also evaluate the performance of the case with controlled flow-rate and compare it with the above results. Consider the following control function which allows flow-rate modulations also deviating by \(50\,\%\) from the steady state values:

$$\begin{aligned} v(t)= {\left\{ \begin{array}{ll} 0.005, &{}\text { if }t\in [0,50)\cup \{100\}, \\ 0.015, &{}\text { if }t\in [50,100), \end{array}\right. } \text { and } \; v(t+100) = v(t) \; \text{ for } \text{ all } \; t\in {\mathbb R}. \end{aligned}$$

and calculate the cost functional (29) for the parameters (38):

$$\begin{aligned} \begin{aligned} J[C_b,v]&=\frac{1}{\tau }\int _0^\tau \left[ C_b(t)^{-(n-1)}+k(n-1)\tau \right] ^{-\frac{1}{n-1}}v(t)dt\\ {}&= 10^{-2}\int _0^{50}\frac{10\,C_{\textrm{max}}}{10+C_{\textrm{max}}}\,v_{\textrm{min}}\,dt+ 10^{-2}\int _{50}^{100}\frac{10\,C_{\textrm{min}}}{10+C_{\textrm{min}}}\,v_{\textrm{max}}\,dt\\ {}&\approx 6.8323\cdot 10^{-3} \left( \frac{mol}{m^2\,s}\right) . \end{aligned} \end{aligned}$$

Thus, the predicted performance of the two-input control strategy for this scenario is \(23.26\,\%\) better than the single-input bang-bang strategy, and is \(24.84\,\%\) better than the steady-state.

4.2 The Impact of “Forcing Parameters”

In this subsection, we investigate the role of control design parameters that could impact the performance of the reaction model. Usually, authors investigate the frequency of switching, the phase shift with two controls, and the amplitude as “forcing parameters” (see, e.g., [6]).

Once the period of operation \(\tau \) is fixed, the frequency of the switching for the bang-bang strategy does not impact the performance (see Remarks 2.1, 3.1). So, the number and the frequency of switchings can be chosen arbitrarily, provided that the measure of appropriate sets in Theorems 2.1 and 3.1 is preserved.

It has been noted in the proof of Theorem 3.1 that the main principle of optimizing the phase shift (as the difference between switching times of the two controls) is that the minimum concentration should be at the same time when the maximum flow-rate is applied. So, if \(\overline{C}-C_{\textrm{min}}=C_{\textrm{max}}-\overline{C}\) and \(\overline{v}-v_{\textrm{min}}=v_{\textrm{max}}-\overline{v}\), then the switching point(-s) should be the same for both controls, and the values should be opposite.

Now we study the amplitude impact. We call \(\alpha :=\frac{\overline{C}-C_{\textrm{min}}}{\overline{C}}\) the concentration amplitude under the assumption \(\overline{C}-C_{\textrm{min}}=C_{\textrm{max}}-\overline{C}\). Similarly, we define the flow-rate amplitude as the value \(\beta :=\frac{\overline{v}-v_{\textrm{min}}}{\overline{v}}\) under the assumption \(\overline{v}-v_{\textrm{min}}=v_{\textrm{max}}-\overline{v}\). It is obvious that these amplitude values are considered in the range (0, 1).

For the single-input case from Sect. 2, we consider the cost function for bang-bang controls as a function of the concentration amplitude \(\alpha \). If the parameters are given by (38) with varying concentration amplitude \(\alpha \), then the cost functional (10) takes the form

$$\begin{aligned} J[C_{b}]= & {} J_\alpha [C_{b}]=\frac{v}{\tau }\int _0^\tau \varPhi (C_b(t))\,dt \nonumber \\= & {} 5\cdot 10^{-3}\left( \varPhi \left( \overline{C}(1+\alpha )\right) + \varPhi \left( \overline{C}(1-\alpha )\right) \right) \nonumber \\= & {} 5\cdot 10^{-3}\left( \frac{10(1+\alpha )}{11+\alpha }+ \frac{10(1-\alpha )}{11-\alpha }\right) = \frac{\alpha ^2-11}{10\alpha ^2-1210}. \end{aligned}$$
(39)

The amplitude dependence is illustrated in Fig. 2a. One can see that the larger the amplitude, the better the performance is. Now we investigate the potential for improvement. For this purpose, we define the following function which shows the percentage of improvement in comparison with the steady-state:

$$\begin{aligned} P_{C_{b},\overline{C}}(\alpha )=100\left( 1-\frac{J_\alpha [C_b]}{J[\overline{C}]}\right) = \frac{1000\alpha ^2}{121-\alpha ^2}. \end{aligned}$$
(40)

The graph of the function \(P_{C_{b},\overline{C}}(\alpha )\) is shown in Fig. 2b. As one can see, the performance can be improved up to \(8.26\,\%\) in comparison with the steady-state. But it should be taken into account that, in the limiting case \(\alpha =1\), the concentration is zero for half of the time period (and thus there is no chemical reaction at all).

Fig. 2
figure 2

The graphs of the cost functional J from (39) and the percentage function P from (40) as functions of the concentration amplitude \(\alpha \) under the choice of parameters (38)

Full size image

Considering the case with two control functions from Sect. 3, we can investigate the same dependencies. Namely, the cost functional has the following form:

$$\begin{aligned} J[C_{b},v_b]= & {} J_{\alpha ,\beta }[C_{b},v_b]=\frac{1}{\tau }\int _0^\tau \varPsi (C_b(t))\,v_b(t)\,dt \nonumber \\ {}= & {} \frac{\overline{v}}{2}\left( \varPsi \left( \overline{C}(1+\alpha )\right) (1-\beta )+ \varPsi \left( \overline{C}(1-\alpha )\right) (1+\beta )\right) \nonumber \\= & {} 5\cdot 10^{-3}\left( \frac{10(1+\alpha )(1-\beta )}{11+\alpha }+ \frac{10(1-\alpha )(1+\beta )}{11-\alpha }\right) \nonumber \\= & {} \frac{\alpha ^2+10\alpha \beta -11}{10\alpha ^2-1210}. \end{aligned}$$
(41)

Thus, the percentage function takes the form:

$$\begin{aligned} P_{C_{b},\overline{C}}(\alpha ,\beta )=100\left( 1-\frac{J_{\alpha ,\beta }[C_b,v_b]}{J[\overline{C},\overline{v}]}\right) = \frac{1000\,\alpha \,(\alpha +11\beta )}{121-\alpha ^2}. \end{aligned}$$
(42)

The graphs of the cost and the percentage function are presented in Fig. 3a and b, respectively. In this case, the performance could be improved theoretically up to \(100\,\%\) (in the case of maximum concentration and flow-rate amplitudes) in comparison with the steady-state.

Fig. 3
figure 3

The cost J from (41) and the percentage function P from (42) depending on the concentration amplitude \(\alpha \) and flow-rate amplitude \(\beta \). The levels with specified values are marked with color lines

Full size image

Remark 4.1

In the limiting cases \(\alpha =1\) or \(\beta =1\), there are situations when the flow-rate is stopped (\(v=0\)) or the inlet concentration vanishes (\(C_{A_0}=0\)), so the reaction is stopped. While this case is the most productive from the mathematical viewpoint, and the bang-bang strategy still has a better performance compared to the steady-state, the investigated mathematical model cannot be used to describe the reaction mechanism in practice. Such limiting cases should be treated separately as our analysis is not directly applicable.

In order to investigate the impact of the time period \(\tau \), we consider the problem (1), (2) with one control input. It is easy to check that the cost functional (10) does not depend on \(\tau \) for the steady-state solution (8) and the case of bang-bang control (9). So, we can not use the time period \(\tau \) as a force parameter to improve the performance in the single input case. We leave the case of two controls for further investigation, as it requires more detailed analysis, especially concerning assumption (21).

5 Conclusion and Future Work

The optimal control problem for an isothermal PFR model with a single periodic input has been completely solved in Sect. 2, and the bang-bang optimal control strategies for periodic chemical reactions in an isothermal PFR with a controlled flow-rate have been proposed in Sect. 3.

Note that the considered cost functional is not convex, and the investigated optimal control problems do not have unique solutions. A well-known approach in the literature (see, e.g., [3, 15] and references therein) is to add regularization terms to the objective functional to ensure the uniqueness of the optimal solution. We do not study such a regularization problem in this work, leaving this issue for further research.

It should also be emphasized that the problem formulations do not include the initial conditions. This omission is because the method of characteristics enables the reconstruction of the complete solution from the boundary control signal alone, after a specified time interval. This consideration introduces a similarity to the turnpike property in optimal control theory, wherein the influence of initial data diminishes over a large time horizon (see, for example, [8]). We consider turnpike analysis to be another prospective topic in the optimal control of chemical reactions, including a more realistic non-isothermal PFR model (see, e.g., [16, 17]).

The optimization of periodic reactions in a Dispersed Flow Tubular Reactor (DFTR) is also a challenging task in this direction. Namely, a parabolic DFTR model [13, p. 394] could be considered in future.