1 Introduction

Two-wheeled inverted pendulum (TWIP, for short) is a general term for mechanical models driven by two wheels with a rod of pendulum mounted on the chassis. It is a self-balancing system and has some remarkable superiorities, such as simple structure, good dexterity, true zero turning radius, small footprint, low cost and low energy consumption [1]. Thus, it has been more and more widely used in human transporters and humanoid robots. However, the dynamics analysis and motion control design of TWIP systems are still challenging, because a TWIP is an essential nonlinear and under-actuated system, and the two wheels of the TWIP are subjected to nonholonomic constraints when the wheels move by rolling rather than slipping. The nonholonomic constraints of a TWIP are described by the motion equations of the mobile chassis, which not only restrain the motion displacement, but also the motion velocity that is not integrable. The flexibility of nonholonomic systems is superior to the holonomic ones, because the state of a mechanical system with nonholonomic constraints can be reached to any location in the displacement space. Thus, in some applications, nonholonomic structures are intentionally introduced to the manipulating device to implement intricate motion functions [2]. Usually, the nonholonomic systems are firstly transformed into chain normal forms. Then, different kinds of control methods, based on chain systems, can be used to design controllers for the original nonholonomic systems [3, 4]. In addition to the chain normal form, power form and Goursat normal form are two other kinds of normal forms, which can be also used to deal with nonholonomic systems [5, 6]. However, the designed controllers based on these kinds of normal forms are focused on speeds, rather than forces or moment of force, which are more aligned with an actual motion control problem of the nonholonomic mechanical system. Thus, the motion equations and dynamics equations of a nonholonomic mechanical system should be simultaneously considered in the control design for implementing a given motion task.

Stabilization of the inverted pendulum is a pre-requisite in many control applications of a TWIP, whereas the strong nonlinearity of the inverted pendulum is a major difficulty in the control design. For some nonlinear Lagrangian mechanical systems, the Chernousko’s decomposition method and its extension [7, 8] have been used for designing constrained feedback control to implement prescribed control objectives. Especially, for a pendulum-like system, a time-optimal feedback control with several switchings which is not greater than one for any initial condition was proposed in [9]. When the external disturbances and system uncertainties are taken into consideration, different kinds of robust control design methods have been designed to stabilize the TWIP, such as combined control with a decoupled LQR controller and two state variable controllers [10, 11]; nonlinear disturbance observer-based dynamic surface control [12]; sliding mode control [13, 14]; adaptive backstepping control [15] and so on. For the motion control design problem of the TWIP, most of the available works about controller design usually use the given longitudinal and yaw rotational speeds as tracking targets. Based on the dynamics equations of the TWIP, neural network-based control [16], fuzzy logic control [17] and adaptive control combined with some classical control methods have been proposed to design trajectory tracking controllers to track the given longitudinal and yaw rotational speeds target [18,19,20,21,22]. However, few works on the TWIP are devoted to design controllers for implementing a given motion trajectory curve in the Cartesian frame. The main difficulty for this motion control problem is that the relationship between the target trajectory curve and the forward and yaw rotation speeds of the TWIP is not clear. In [23, 24], for example, the forward and yaw rotational speeds are considered as the intermediate variables, which are denoted as the control input of the motion equations and the control output of the dynamics equations simultaneously. Then, a composite controller for implementing a given motion task is designed by using direct/indirect adaptive fuzzy control to track the trajectory path, plus a sliding mode control to render the stabilizing process of the vehicle body with strong robustness. In [25], two high gain observers are proposed for estimating the forward and yaw rotational speeds of a two-wheeled mobile robot without an inverted pendulum. Then, an adaptive output feedback tracking controller is designed to implement the circular motion by using the estimated velocities. In addition, time delays in controllers and uncertainties from modeling or measurement or perturbation are usually inevitable in real applications, but they are usually ignored in the literature [1]. The most popular methods to deal with input delay are related to the prediction-based compensation control strategy [26,27,28]. However, input delay is very important especially when some robust controls with high-frequency switching mechanism such as sliding mode controls are used, where the existence of input delay would lead to reversed control if the input delay is ignored. In fact, TWIP is a natural high-frequency vibration system, when the rod of pendulum is stabilized at the unstable equilibrium point. As shown in [27], a very small input delay may enlarge the vibration amplitude of the TWIP system remarkably in the trajectory tracking problem by using integral sliding mode control. Therefore, the input delay, although very small, is one of our major concerns in the control design of a TWIP.

In this paper, a controller design method for a TWIP to run along a given trajectory curve is proposed, for which the nonholonomic constraints must be considered. The design consists of two parts: One is the use of curvature theory to tracking the trajectory path precisely, and the other is the use of integral sliding mode control to stabilize the vehicle body robustly. Section 2 is the problem statement, Sect. 3 presents the key observations of the motion laws, Sect. 4 focuses on the controller design based on the observations, Sect. 5 demonstrates the main results with a numerical example, and finally, Sect. 6 ends with some concluding remarks.

Fig. 1
figure 1

Schematic diagram of the TWIP

Full size image
Table 1 The parameters and variables of the TWIP
Full size table

2 Problem Statement

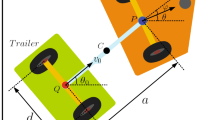
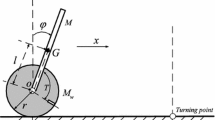
Figure 1 is a schematic diagram of the TWIP model, with the parameters and variables of the TWIP described in Table 1. Two kinds of equations are used to describe the motion of the TWIP: One is the equations featuring the motion of the chassis, and the other is the equations characterizing the dynamical behaviors of the whole TWIP.

Let \(\mathbf{q }=(x_o,y_o,\theta ,\varphi ,\theta _\mathrm{r},\theta _\mathrm{l})\) be the generalized coordinates of the TWIP. If the wheels run under the conditions of pure rolling and nonslipping, then, the motion equations are given by the following nonholonomic constraints

$$\begin{aligned}&-{\dot{x}}_o \mathrm{sin}\theta +{\dot{y}}_o \mathrm{cos}\theta =0 ,\nonumber \\&\quad {\dot{x}}_o \mathrm{cos}\theta +\,{\dot{y}}_o \mathrm{sin}\theta +d\frac{{\dot{\theta }}}{2}-r\dot{\theta _\mathrm{r}}=0,\nonumber \\&\quad {\dot{x}}_o \mathrm{cos}\theta +{\dot{y}}_o \mathrm{sin}\theta -d\frac{{\dot{\theta }}}{2}-r\dot{\theta _\mathrm{l}}=0. \end{aligned}$$
(1)

Let \(v_{T}\), v, \(\omega \) be the lateral speed, forward speed and yaw rotational speed of the mobile chassis, respectively. Then, \({\dot{x}}_o=v\mathrm{cos}\theta \), \({\dot{y}}_o=v\mathrm{sin}\theta \), and the motion equations, namely Eq. (1), are equivalent to the following equations

$$\begin{aligned} v_{T}= & {} -{\dot{x}}_o \mathrm{sin}\theta +{\dot{y}}_o \mathrm{cos}\theta =0 ,\nonumber \\ v= & {} {\dot{x}}_o \mathrm{cos}\theta +{\dot{y}}_o \mathrm{sin}\theta =\frac{r}{2}(\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}}),\nonumber \\ \omega= & {} {\dot{\theta }}=\frac{r}{d}(\dot{\theta _\mathrm{r}}-\dot{\theta _\mathrm{l}}). \end{aligned}$$
(2)

The dynamics equations of the TWIP model can be obtained by using the Euler–Lagrange equations for nonholonomic systems as done in our previous paper [28]:

$$\begin{aligned} \left. \begin{aligned} \ddot{\varphi }=&\frac{1}{\varDelta +M^2 l^2 r^2 \mathrm{cos}^2\varphi }[-Ml({\dot{\theta }}^2 l\mathrm{cos}\varphi +g)(Mr^2\mathrm{sin}\varphi \\&+2I_\mathrm{w} \mathrm{sin}\varphi +2M_\mathrm{w} r^2\mathrm{sin}\varphi )+M^2 l^2r^2 {\dot{\varphi }}^2 \mathrm{sin}\varphi \mathrm{cos}\varphi ] \\&+\frac{Mr^2+2I_\mathrm{w}+2M_\mathrm{w} r^2+Mlr{\cos }\varphi }{\varDelta +M^2 l^2 r^2 \mathrm{cos}^2\varphi }u_2, \\ {\dot{v}}=&\frac{1}{\varDelta +M^2 l^2 r^2 \mathrm{cos}^2\varphi }[M^2 l^2 r^2\mathrm{sin}\varphi \mathrm{cos}\varphi ({\dot{\theta }}^2 l\mathrm{cos}\varphi +g)\\&-M^2 l^3 r^2{\dot{\varphi }}^2\mathrm{sin}\varphi -I_\mathrm{B} M l r^2 {\dot{\varphi }}^2\mathrm{sin}\varphi ] \\&-\frac{Mlr^2\mathrm{cos}\varphi +Mrl^2+I_\mathrm{B} r}{\varDelta +M^2 l^2 r^2 \mathrm{cos}^2\varphi }u_2, \\ \ddot{\theta }=&\frac{2Mr^2 l^2{\dot{\theta }}{\dot{\varphi }}\mathrm{sin}2\varphi }{\varOmega +2Ml^2 r^2 \mathrm{cos}^2\varphi }+\frac{rd}{\varOmega +2Ml^2 r^2 \mathrm{cos}^2\varphi }u_1, \end{aligned} \right\} \end{aligned}$$
(3)

where

$$\begin{aligned} \varDelta= & {} -M^2 l^2 r^2-2Ml^2 I_\mathrm{w}-2Ml^2 M_\mathrm{w} r^2-I_\mathrm{B} Mr^2-2I_\mathrm{B} I_\mathrm{w}-2M_\mathrm{w} r^2 I_\mathrm{B},\\ \varOmega= & {} -M_\mathrm{w} d^2 r^2-4I_\mathrm{wd}r^2-2I_Z r^2-d^2 I_\mathrm{w}-2Ml^2 r^2,~u_1=T_\mathrm{l}-T_\mathrm{r},~u_2=T_\mathrm{l}+T_\mathrm{r}, \end{aligned}$$

\(u_1\) and \(u_2\) are the torque controllers acted on the wheels. Equation (3) is nonlinear, its control design is usually difficult by using the prediction-based control methods [26], especially when the input delay is taken into account. However, the control task requires that \(\varphi \) is small during the whole motion process, so the control design can be based on the linearized equation with respect to \(\varphi \) round \(\varphi =0\). Let \(\mathbf{X }=[x_1,x_2,x_3,x_4]^\mathrm{T}=[\varphi ,{\dot{\varphi }},x,v]^{\mathrm{T}}\) be the state vector, and

$$\begin{aligned} \mathbf{A }_{0}(t)=\left[ \begin{array}{cccc} 0&{} \quad 1&{} \quad 0&{}\quad 0 \\ \frac{-Ml(\omega ^2 l+g)(Mr^2+2I_\mathrm{w}+2M_\mathrm{w} r^2)}{\varDelta +M^2 l^2 r^2}&{} \quad 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \frac{M^2 l^2 r^2 (\omega ^2 l+g)}{\varDelta +M^2 l^2 r^2}&{}\quad 0&{}\quad 0&{}\quad 0 \end{array} \right] ,\quad \mathbf{B }=\left[ \begin{array}{c} ~~0 \\ \frac{Mr^2+2I_\mathrm{w}+2M_\mathrm{w} r^2+Mlr}{\varDelta +M^2 l^2 r^2} \\ ~~ 0 \\ -\frac{Mlr^2+Mrl^2+I_\mathrm{B} r}{\varDelta +M^2 l^2 r^2} \\ \end{array} \right] . \end{aligned}$$

where \(\mathbf{A }_0(t)\) is time-variant due to the time-dependence of \(\omega (t)\). Then, the linearized equation is given by

$$\begin{aligned}&\displaystyle \dot{\mathbf{X }}(t)=\mathbf{A }_{0}(t)\mathbf{X }(t)+\mathbf{B }u_2(t-\tau ), \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \ddot{\theta }={\dot{\omega }}=\frac{rd}{\varOmega +2Ml^2 r^2}u_1(t-\tau ), \end{aligned}$$
(5)

if the input delay \(\tau >0\) is taken into account. Taking model uncertainty, linearization error and external disturbances into account, Eqs. (4), (5) are represented as

$$\begin{aligned}&\displaystyle \dot{\mathbf{X }}(t)=\mathbf{A }_{0}(t)\mathbf{X }(t)+\mathbf{B }u_2(t-\tau )+\varvec{\sigma }_{1}^{0}(t), \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle {\dot{\omega }}=\frac{rd}{\varOmega +2Ml^2 r^2}u_1(t-\tau )+\sigma _2(t), \end{aligned}$$
(7)

respectively, where \(\varvec{\sigma }_{1}^{0}(t)\) and \(\sigma _2(t)\) stand for the integration of the model uncertainty, linearization error and bounded external disturbances.

The control objective is to design a delayed controller \((u_1(t-\tau ),u_2(t-\tau ))\), so that the TWIP runs along a pre-settled pathway \(\varGamma (t)=(x_o(t),y_o(t))\) and keeps the tilt angle \(\varphi \) small enough.

Fig. 2
figure 2

The turning motion to the left of the mobile chassis

Full size image

3 Key Observations about Motion Equations

For clarity in presentation, the turning motion is made in a plane, and \(\dot{\theta _\mathrm{r}}>\dot{\theta _\mathrm{l}}>0\) is assumed to be true, so that the mobile chassis turns to the left in the plane, as shown in Fig. 2. A key observation of this paper is that a pair of known rotational speed \((\dot{\theta _\mathrm{r}},\dot{\theta _\mathrm{l}})\) of the two wheels determines uniquely a motion trajectory curve \((x_o(t),y_o(t))\) to the center point O, and conversely a known motion trajectory curve \((x_o(t),y_o(t))\) of the center point O determines uniquely a pair of rotational speed \((\dot{\theta _\mathrm{r}},\dot{\theta _\mathrm{l}})\) to the two wheels. More precisely, one has

Theorem 3.1

Let \((\dot{\theta _\mathrm{r}},\dot{\theta _\mathrm{l}})\) be the pair of rotational speed of the two wheels, \((x_o(t),y_o(t))\) be the coordinate of the motion trajectory curve to the center point O, \(k_o(t)\) be the relative curvature of the trajectory curve, v and \({\dot{\theta }}\) be the forward speed and yaw rotational speed of the mobile chassis, respectively. Then,

$$\begin{aligned} \dot{\theta _\mathrm{r}}=\frac{1}{r}\sqrt{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}+\frac{d}{2 r}\frac{{\dot{x}}_{o}\ddot{y}_{o}-\ddot{x}_{o}{\dot{y}}_{o}}{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2} ,~ \dot{\theta _\mathrm{l}}=\frac{1}{ r}\sqrt{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}-\frac{d}{2 r}\frac{{\dot{x}}_{o}\ddot{y}_{o}-\ddot{x}_{o}{\dot{y}}_{o}}{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}, \end{aligned}$$
(8)

and

$$\begin{aligned} v= \sqrt{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2} ,~ {\dot{\theta }}= \frac{{\dot{x}}_{o}\ddot{y}_{o}-\ddot{x}_{o}{\dot{y}}_{o}}{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}=k_o(t)v(t). \end{aligned}$$
(9)

Proof

In a very small time interval \([t,~~t+\varDelta t]\), the movement distance of the two wheels can be approximated as \(\dot{\theta _\mathrm{l}}(t)r\varDelta t\) and \(\dot{\theta _\mathrm{l}}(t)r\varDelta t\), respectively. Thus, due to the effect of nonholonomic constraints, one has

$$\begin{aligned} \frac{\dot{\theta _\mathrm{l}}r\varDelta t }{R_l}=\frac{\dot{\theta _\mathrm{r}}r\varDelta t }{R_r}, \end{aligned}$$
(10)

where \(R_\mathrm{l},~R_\mathrm{r}\) are the turning radius of the two wheels, and \(R_\mathrm{r}=R_\mathrm{l}+d\). It follows that

$$\begin{aligned} R_\mathrm{l}=\frac{d\dot{\theta _\mathrm{l}}}{\dot{\theta _\mathrm{r}}-\dot{\theta _\mathrm{l}}},\quad R_\mathrm{r}=\frac{d\dot{\theta _\mathrm{r}}}{\dot{\theta _\mathrm{r}}-\dot{\theta _\mathrm{l}}}, \end{aligned}$$

due to Eq. (10). Therefore, the turning radius of the center point O is

$$\begin{aligned} R_o=\frac{d}{2}\frac{\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}}}{\dot{\theta _\mathrm{r}}-\dot{\theta _\mathrm{l}}}, \end{aligned}$$
(11)

and the corresponding relative curvature is

$$\begin{aligned} k_{o}(t)=\frac{1}{R_o}=\frac{2}{d}\frac{\dot{\theta _\mathrm{r}}-\dot{\theta _\mathrm{l}}}{\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}}}, \end{aligned}$$
(12)

which depends on t, and can also be transformed to a function with respect to the length arc variable, described by

$$\begin{aligned} s(t)=\frac{r}{2} \int _0^{t}(\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}})\mathrm{d}\xi =\frac{r}{2}(\theta _\mathrm{r}+\theta _\mathrm{l}). \end{aligned}$$
(13)

Under the assumption \(\dot{\theta _\mathrm{r}}>\dot{\theta _\mathrm{l}}>0\), one has \( {\dot{s}}(t)=\frac{r}{2} (\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}})>0, \) which means that Eq. (13) defines an one-to-one mapping between the arc length variable and the time variable. Hence,

$$\begin{aligned} k_{o}(t)=\dfrac{2}{d}\dfrac{\dfrac{\mathrm{d} \theta _\mathrm{r}}{\mathrm{d} t}-\dfrac{\mathrm{d} \theta _\mathrm{l}}{\mathrm{d} t}}{\dfrac{\mathrm{d} \theta _\mathrm{r}}{\mathrm{d} t}+\dfrac{\mathrm{d} \theta _\mathrm{l}}{\mathrm{d} t}}=\dfrac{2}{d}\dfrac{\dfrac{\mathrm{d} \theta _\mathrm{r}}{\mathrm{d} s}\dfrac{\mathrm{d} s}{\mathrm{d} t}-\dfrac{\mathrm{d} \theta _\mathrm{l}}{\mathrm{d} s}\dfrac{\mathrm{d} s}{\mathrm{d} t}}{\dfrac{\mathrm{d} \theta _\mathrm{r}}{\mathrm{d} s}\dfrac{\mathrm{d} s}{\mathrm{d} t}+\dfrac{\mathrm{d} \theta _\mathrm{l}}{\mathrm{d} s}\dfrac{\mathrm{d} s}{\mathrm{d} t}} =\dfrac{2}{d}\dfrac{\dfrac{\mathrm{d} \theta _\mathrm{r}}{\mathrm{d} s}-\dfrac{\mathrm{d} \theta _\mathrm{l}}{\mathrm{d} s}}{\dfrac{\mathrm{d} \theta _\mathrm{r}}{\mathrm{d} s}+\dfrac{\mathrm{d} \theta _\mathrm{l}}{\mathrm{d} s}} ={\hat{k}}_{o}(s). \end{aligned}$$
(14)

According to planar curve theory [29] and Eq. (14), the smooth function \({\hat{k}}_{o}(s)\) determines uniquely a smooth curve \(r(s)=(x_o(s),y_o(s))\). Substituting Eq. (13) into r(s), the trajectory curve \((x_o(t),y_o(t))\) can be easily calculated.

On the other hand, the required rotational speed of two wheels can also be obtained if the motion trajectory curve of the mobile chassis is given. Actually, \(k_o(t)\) can be expressed in the following formula

$$\begin{aligned} k_{o}(t)=\frac{{\dot{x}}_{o}\ddot{y}_{o}-\ddot{x}_{o}{\dot{y}}_{o}}{({\dot{x}}_{o}^2+{\dot{y}}_{o}^2)^{\frac{3}{2}}}. \end{aligned}$$
(15)

According to Eq. (12), it goes to

$$\begin{aligned} \frac{2}{d}\frac{\dot{\theta _\mathrm{r}}-\dot{\theta _\mathrm{l}}}{\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}}} =\frac{{\dot{x}}_{o}\ddot{y}_{o}-\ddot{x}_{o}{\dot{y}}_{o}}{({\dot{x}}_{o}^2+{\dot{y}}_{o}^2)^{\frac{3}{2}}}. \end{aligned}$$
(16)

In addition, since

$$\begin{aligned} s(t)=\frac{r}{2} \int _0^{t}(\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}})\mathrm{d}\xi =\int _0^{t}\sqrt{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}\mathrm{d}\xi . \end{aligned}$$
(17)

Then, by differentiation with respect to t, one has

$$\begin{aligned} \frac{r}{2} (\dot{\theta _\mathrm{r}}+\dot{\theta _\mathrm{l}})=\sqrt{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}. \end{aligned}$$
(18)

Solving the rotational speed \((\dot{\theta _\mathrm{r}},\dot{\theta _\mathrm{l}})\) from Eqs. (16)–(18) gives Eq. (8), and substituting (8) to (2) gives (9). \(\square \)

Let \(\varGamma (s)=(x_o(s),y_o(s))~(s\in [0,l])\) be used for describing the pre-determined control pathway, where s is the arc length variable. Then, the tangent vector of \(\varGamma (s)\) must be an unit vector due to

$$\begin{aligned} \left| \ \frac{\mathrm{d}\varGamma (s)}{\mathrm{d}s}\right| =\sqrt{\left( \frac{\mathrm{d} x_o}{\mathrm{d}s}\right) ^{2}+\left( \frac{\mathrm{d} y_o}{\mathrm{d}s}\right) ^{2}}=1. \end{aligned}$$

Thus, the initial forward speed target would be a constant if \(\varGamma (t)=(x_o(t),y_o(t)),(s=t)\) is chosen as the trajectory tracking target. In this case, the initial speed error does not approach zero due to the fact that the initial velocity of the TWIP is zero. Thus, the actual location error of the TWIP would accumulate and becomes larger and larger due to the errors from the forward speed and the yaw rotation speed.

To reduce the initial speed error, an one-to-one smooth mapping \(s=\phi (t)\) is introduced. Then, the trajectory tracking target is given by \({\hat{\varGamma }}(t)=(x_o(\phi (t)),y_o(\phi (t))).\) It follows that

$$\begin{aligned} |\dot{{\hat{\varGamma }}}(t)|=\sqrt{\left( \frac{\mathrm{d}x_o}{\mathrm{d}s}\right) ^{2}+\left( \frac{\mathrm{d} x_o}{\mathrm{d}s}\right) ^{2}}\;|{\dot{\phi }}(t)|=|{\dot{\phi }}(t)|\,. \end{aligned}$$

Thus, in order that the initial speed error is zero and without jumping, the function \(\phi (t)\) is required to satisfy

$$\begin{aligned} {\lim _{t \rightarrow 0}}{\dot{\phi }}(t)=0,~{\dot{\phi }}(0)=0, \end{aligned}$$
(19)

such a function can be chosen in different ways. For example, if the speed of the TWIP is expected to be zero, when the motion task is finished, the function \(\phi (t)\) can be chosen to satisfy \({\dot{\phi }}(t)=\alpha t \mathrm{e}^{-\beta t}\). In this case,

$$\begin{aligned} \phi (t)=-\frac{(\beta t+1)\alpha \mathrm{e}^{-\beta t}}{\beta ^2}+\gamma , \end{aligned}$$

where \(\alpha>0,~\beta >0\) and \(\gamma >0\) are parameters to be determined from

$$\begin{aligned} \int _{0}^{+\infty }{\dot{\phi }}(t)\mathrm{d}t=l, \quad \phi (0)=0. \end{aligned}$$

Hence, \(\gamma =l,~~\alpha =l \beta ^2,\) and \({v}={\dot{\phi }}=l\beta ^2 t\mathrm{e}^{-\beta t}\). In this case, the smooth function \(s=\phi (t)\) is found to

$$\begin{aligned} \phi (t)=-(\beta t+1)l \mathrm{e}^{-\beta t}+l. \end{aligned}$$
(20)

Lemma 3.1

For a given motion task path \(\varGamma (s)=(x_o(s),y_o(s)),~s\in [0,l]\), the one-to-one smooth mapping (20) can be used for designing a trajectory tracking target \(\varGamma (t)=(x_o(\phi (t)),y_o(\phi (t)))\), which has zero initial velocity and zero terminal velocity.

4 Controller Design Based on Curvature Tracking and Optimal Control

The control problems of a TWIP can be roughly classified into two categories: trajectory planning and controller design, which are usually studied separately in the literature. In this section, trajectory planning plays a very important role in the controller design.

4.1 A Dynamical Trajectory Tracking Target

Note that the dynamics equation (3) merely described the relationship between the control variables and the forward speed and yaw rotation speed of the TWIP, and the position coordinate \((x_o(t),y_o(t))\) is implemented indirectly by the forward speed and yaw rotation speed. Therefore, any tracking error of position with two position coordinates \(x_o(t)\) and \(y_o(t)\) may cause inward movement or outward movement, and consequently, tracking \((x_o(t),y_o(t))\) may lead to large error of the position with the increases of the error accumulation. However, the smooth curvature function \(k_o(t)\) fully determines the shape of a trajectory curve \(\varGamma (t)=(x_o(t),y_o(t))\), the difference between two curve expressions with the same curvature is nothing but tangential speed. This means that when \(k_o(t)\) is tracked, \(\varGamma (t)\) is tracked accordingly no matter what the tangential speed is. Thus, for the trajectory tracking problem, it is very important to keep \(k_o(t)\) well tracked, while the speed v(t) of the TWIP can be either slow or not slow. Due to \(\omega (t)=k_o(t)v(t)\), the relationship among the actual yaw rotational speed, actual forward speed and the curvature of the actual motion trajectory curve, \(k_o(t)\) is tracked if the dynamical tracking target \({\tilde{\omega }}(t)=k_o(t)v(t)\) is tracked. Let \({\tilde{v}}={\dot{\phi }}(t)\) be chosen as a static tracking target of v(t) with a smooth function \(\phi (t)\) satisfying (19). Then, one has

Theorem 4.1

Let \(\varGamma (s)=(x_o(s),y_o(s)),~s\in [0,l]\) be a given trajectory curve, \(k_{o}(s)\) be the relative curvature of \(\varGamma (s)\), and v(t) be the actual forward speed of the TWIP. Then, the dynamical trajectory tracking target for implementing the motion task of walking along the given curve \(\varGamma (s)\) can be designed as

$$\begin{aligned} {\tilde{v}}={\dot{\phi }}(t), ~ {\tilde{\omega }}=k_o(\phi (t))v(t). \end{aligned}$$
(21)

where \(s=\phi (t)\) is an one-to-one smooth mapping required in Lemma 3.1.

As a matter of fact, \({\tilde{v}}\) is a pre-determined tracking target, which can be pre-adjusted for better control effect in an actual problem. However, the so-called dynamics tracking target \({\tilde{\omega }}\) is state-dependent with the actual forward speed, which is varying dynamically from moment to moment.

4.2 Optimal Integral Sliding Mode Control Design

Because Eqs. (6) and (7) are decoupled, the controllers \(u_1(t-\tau )\) and \(u_2(t-\tau )\) can be designed separately.

The matrix \(\mathbf{A }_{0}(t)\) in Eq. (6) is time-variant and can be decomposed into \(\mathbf{A }_{0}(t)=\mathbf{A }+\varDelta \mathbf{A }\), where

$$\begin{aligned} \mathbf{A }= & {} \left[ \begin{array}{cccc} 0&{}\quad 1&{} \quad 0&{}\quad 0 \\ \frac{-Mlg(Mr^2+2I_\mathrm{w}+2M_\mathrm{w} r^2)}{\varDelta +M^2 l^2 r^2}&{}\quad 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \frac{M^2 l^2 r^2 g}{\varDelta +M^2 l^2 r^2}&{}\quad 0&{}\quad 0&{}\quad 0 \end{array} \right] , \quad \\ \varDelta \mathbf{A }= & {} \left[ \begin{array}{cccc} 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \frac{-Ml\omega ^2 l(Mr^2+2I_\mathrm{w}+2M_\mathrm{w} r^2)}{\varDelta +M^2 l^2 r^2}&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \frac{M^2 l^2 r^2 \omega ^2 l}{\varDelta +M^2 l^2 r^2}&{}\quad 0&{}\quad 0&{}\quad 0 \end{array} \right] . \end{aligned}$$

The modeling error \(\varDelta \mathbf{A }\mathbf{X }(t)\) of the linearized system is

$$\begin{aligned} \left[ 0, \frac{-Ml\omega ^2 l(Mr^2+2I_\mathrm{w}+2M_\mathrm{w} r^2)}{\varDelta +M^2 l^2 r^2}\theta ,0,\frac{M^2 l^2 r^2 \omega ^2 l}{\varDelta +M^2 l^2 r^2}\theta \right] ^{\mathrm{T}}. \end{aligned}$$

System (6) can be rewritten as the following equation if slow motion speed of the TWIP is considered

$$\begin{aligned} \dot{\mathbf{X }}(t)=\mathbf{A }\mathbf{X }(t)+\mathbf{B }u_2(t-\tau )+\varvec{\sigma }_1(t), \end{aligned}$$
(22)

where the error part \(\varDelta \mathbf{A }\mathbf{X }(t)\) is combined into \(\varvec{\sigma }_1(t)\), and \(\varvec{\sigma }_1(t)=\varvec{\sigma }_{1}^{0}(t)+\varDelta \mathbf{A }\mathbf{X }(t)\).

Let \(\tilde{\mathbf{X }}=[{\tilde{x}}_1,{\tilde{x}}_2,{\tilde{x}}_3,{\tilde{x}}_4]^\mathrm{T}=[0,0,{\tilde{x}},{\tilde{v}}]^{\mathrm{T}}\) be the trajectory tracking target vector to be designed according to the given motion task, \(\mathbf{Y }(t)=\mathbf{X }(t)-\tilde{\mathbf{X }}(t)\) be the error vector of system (22), and \(\varvec{\eta }_{1}(t):=\mathbf{A }\tilde{\mathbf{X }}-\dot{\tilde{\mathbf{X }}}\). Then, system (22) governing the tracking error takes the form

$$\begin{aligned} \dot{\mathbf{Y }}(t)=\mathbf{A }\mathbf{Y }(t)+\mathbf{B }u_2(t-\tau )+\varvec{\sigma }_1(t)+\varvec{\eta }_{1}(t). \end{aligned}$$
(23)

In order to have a small tilt angle of the pendulum, so that the control design can be made on the basis of the linearized system, a quadratic performance criterion with large weight of the tilt angle is introduced as follows:

$$\begin{aligned} J=\frac{1}{2}\mathbf{Y }^{\mathrm{T}}(t_f)\mathbf{Q }_{0}\mathbf{Y }(t_f) +\frac{1}{2}\int _0^{t_f}\left[ \mathbf{Y }^\mathrm{T}(t)\mathbf{Q }_{1}\mathbf{Y }(t) +u_{2}^\mathrm{T}(t-\tau )\mathbf{R }u_{2}(t-\tau )\right] \mathrm{d}t,\nonumber \\ \end{aligned}$$
(24)

where \(\mathbf{Q }_{0},\mathbf{Q }_{1}\) are nonnegative definite symmetric matrices, \(\mathbf{R }\) is a positive definite symmetric matrix, and \(t_f\,(>2\tau )\) is the terminal time of the control. With a large weight of the tilt angle error in J, the tilt angle error can be forced to be small enough, when an optimal control is applied. Hence, the linearization error is small and can be considered as bounded. Moreover, for clarity, let \({\tilde{v}}={\dot{\phi }}(t)\) be the tracking target of the forward speed v(t) with \({\dot{\phi }}=l\beta ^2 t\mathrm{e}^{-\beta t}\). So v(t) becomes small if the target speed is small by using a small number \(\beta \). It follows that the yaw rotational speed \(\omega (t)\) is small enough, and consequently, \(\varDelta \mathbf{A }\mathbf{X }(t)\) becomes small enough, when the quadratic performance criterion (24) is minimized. In this way, there is a constant \(D_1 > 0\) such that

$$\begin{aligned} \Vert \varvec{\sigma }_1(t)\Vert \le D_1. \end{aligned}$$
(25)

Usually, it is not an easy task to solve the Riccati differential equation for the LQR optimal control problem, when \(t_f>0\) in Eq. (24) is finite. For any given sufficiently small \(\varepsilon >0\), a real number \(\beta \) may be chosen to satisfy

$$\begin{aligned} \int _{0}^{t_f}{\dot{\phi }}(t)\mathrm{d}t=l-\varepsilon . \end{aligned}$$
(26)

This means that the controller can be designed simply by solving an algebraic Riccati equation if the performance criterion (24) is replaced by

$$\begin{aligned} J=\frac{1}{2}\int _0^{+\infty }\left[ \mathbf{Y }^\mathrm{T}(t)\mathbf{Q }_{1}\mathbf{Y }(t)+u_{2}^\mathrm{T}(t-\tau )\mathbf{R }u_{2}(t-\tau )\right] \mathrm{d}t. \end{aligned}$$
(27)

Here, the trajectory tracking target design is very important in the turning motion control problem of the TWIP. According to Lemma 3.1, the designed trajectory tracking target with zero initial velocity and zero terminal velocity is in agreement with the actual problem in most cases. This leads to a small location error in the whole process and a simple algebraic Riccati equation to be solved. Moreover, small forward velocity of the trajectory tracking target can be designed to keep the tilt angle of the pendulum small enough by choosing a small parameter \(\beta \).

Now, it is in the position to design the controller by following the method proposed in [27]. Firstly, by introducing an integral transformation given by

$$\begin{aligned} \mathbf{Z }(t)=\mathbf{Y }(t)+\int _{t-\tau }^t\mathrm{e}^{-\mathbf{A }(\rho -t+\tau )}[\mathbf{B }u_2(\rho )+\varvec{\eta }_1(\rho +\tau ) +\varvec{\sigma }_1(\rho +\tau )]\mathrm{d}\rho , \end{aligned}$$
(28)

the delayed system (23) is transformed into an equivalent delay-free system as follows:

$$\begin{aligned} \dot{\mathbf{Z }}(t)=\mathbf{A }\mathbf{Z }(t)+\mathbf{B }_0u_2(t)+\mathrm{e}^{-\mathbf{A }\tau } \varvec{\eta }_1(t+\tau )+\mathrm{e}^{-\mathbf{A }\tau } \varvec{\sigma }_1(t+\tau ), \end{aligned}$$
(29)

where \(\mathbf{B }_0=\mathrm{e}^{-\mathbf{A }\tau }\mathbf{B }\), the new state \(\mathbf{Z }(t)\) and the error state \(\mathbf{Y }(t)\) satisfy the following relationship [27]

$$\begin{aligned} \mathbf{Y }(t+\tau ) =\mathrm{e}^{\mathbf{A }\tau }\mathbf{Z }(t). \end{aligned}$$
(30)

With \(\tilde{\mathbf{Q }}_{1}=\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^{\mathrm{T}}\mathbf{Q }_{1}\mathrm{e}^{\mathbf{A }\tau },\,\tilde{\mathbf{Q }}_{0}=\left( \mathrm{e}^{\mathbf{A }\tau }\right) ^{\mathrm{T}}\mathbf{Q }_{0}\mathrm{e}^{\mathbf{A }\tau }\), the quadratic performance criterion can be rewritten as

$$\begin{aligned} J=J_{1}+J_{2}= & {} \frac{1}{2}\int _0^{\tau }\mathbf{Y }^\mathrm{T}(t)\mathbf{Q }_{1}\mathbf{Y }(t)\mathrm{d}t\nonumber \\&+\,\frac{1}{2}\mathbf{Z }^\mathrm{T}(t_{f}-\tau )\tilde{\mathbf{Q }}_{0}\mathbf{Z }(t_{f}-\tau )\nonumber \\&+\,\frac{1}{2}\int _0^{t_{f}-\tau }\left[ \mathbf{Z }^\mathrm{T}(t)\tilde{\mathbf{Q }}_{1}\mathbf{Z }(t)+u_{2}^\mathrm{T}(t)\mathbf{R }u_{2}(t)\right] \mathrm{d}t, \end{aligned}$$
(31)

where \(J_1=\frac{1}{2}\int _0^{\tau }\mathbf{Y }^\mathrm{T}(t)\mathbf{Q }_{1}\mathbf{Y }(t)\mathrm{d}t\) is fixed, because the control does not take effect when \(t\in [0,\tau [\).

The nominal system of (29) is given by

$$\begin{aligned} \dot{\mathbf{Z }}(t)=\mathbf{A }\mathbf{Z }(t)+\mathbf{B }_0u_2(t)+\mathrm{e}^{-\mathbf{A }\tau } \varvec{\eta }_1(t+\tau ). \end{aligned}$$
(32)

According to [27], the optimal control of system (32) that minimizes the quadratic performance criterion J is

$$\begin{aligned} u_2^{*}(t)=-\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}[\mathbf{P }_z(t)\mathbf{Z }(t)+\mathbf{b }_z(t)], \end{aligned}$$
(33)

where \(\mathbf{P }_z(t)\in {\mathbb {R}}^{n\times n}\) and \(\mathbf{b }_z(t)\in {\mathbb {R}}^{n}\) are the solutions of the following Riccati differential equations

$$\begin{aligned}&\displaystyle \dot{\mathbf{P }_z}=-\mathbf{P }_{z}\mathbf{A }-\mathbf{A }^\mathrm{T}\mathbf{P }_z+\mathbf{P }_{z}\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}\mathbf{P }_z-\tilde{\mathbf{Q }}_{1}, ~ \mathbf{P }_z(t_f-\tau )=\tilde{\mathbf{Q }}_{0}, \end{aligned}$$
(34)
$$\begin{aligned}&\displaystyle \dot{\mathbf{b }}_{z}=-[\mathbf{A }-\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_{0}^\mathrm{T}\mathbf{P }_{z}]^{\mathrm{T}}\mathbf{b }_{z}-\mathbf{P }_{z}\mathrm{e}^{-\mathbf{A }\tau }\varvec{\eta }_{1}(t+\tau ), ~ \mathbf{b }_{z}(t_f-\tau )=\mathbf{0 }. \end{aligned}$$
(35)

In order to design a robust controller against the effect of \(\varvec{\sigma }_1(t+\tau )\), the optimal state of the normal system (32) is chosen as the integral sliding mode manifold. Let the sliding mode function be

$$\begin{aligned} \varvec{\digamma }_1(\mathbf{Z }(t)):= & {} \mathbf{G }[\mathbf{Z }(t)-\mathbf{Z }^{*}(0)] -\mathbf{G }\int _0^{t}[(\mathbf{A }-\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_{0}^\mathrm{T}\mathbf{P }_{z})\mathbf{Z }(\rho )\nonumber \\&-\,\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_{0}^\mathrm{T}\mathbf{b }_z(\rho )+\mathrm{e}^{-\mathbf{A }\tau }\varvec{\eta }_1(\rho +\tau )]\mathrm{d}\rho , \end{aligned}$$
(36)

where \(\mathbf{G }\in {\mathbb {R}}^{m\times n}\) is a constant matrix, and \(\mathbf{G }\mathbf{B }_0\) is assumed nonsingular, and \(\mathbf{Z }^{*}(0)\) is the initial value of the nominal system (32) described by

$$\begin{aligned} \mathbf{Z }^{*}(0)=\mathrm{e}^{-\mathbf{A }\tau }(\mathrm{e}^{\mathbf{A }\tau }\mathbf{Y }(0)+\mathrm{e}^{\mathbf{A }\tau }\int _{0}^{\tau }\mathrm{e}^{-\mathbf{A }\rho }\varvec{\eta }_1(\rho )\mathrm{d}\rho )=\mathbf{Y }(0)+\int _{0}^{\tau }\mathrm{e}^{-\mathbf{A }\rho }\varvec{\eta }_1(\rho )\mathrm{d}\rho , \end{aligned}$$

\(\varvec{\digamma }_1(\mathbf{Z }(t))=\mathbf{0 }\) is the sliding mode manifold, which is actually the optimal state of the nominal system (32). Thus, according to Eq. (30), the delayed robust optimal controller of system (23) is given by

$$\begin{aligned} u_2(t-\tau )=u_{20}(t-\tau )+u_{21}(t-\tau ),\quad t\in [\tau ,t_f], \end{aligned}$$
(37)

where

$$\begin{aligned} u_{20}(t-\tau )= & {} -\mathbf{R }^{-1}\mathbf{B }_{0}^\mathrm{T}[\mathbf{P }_{z}(t-\tau )\mathrm{e}^{-\mathbf{A }\tau }\bar{\mathbf{Y }}(t)+\mathbf{b }_{z}(t-\tau )], \\ u_{21}(t-\tau )= & {} -(\mathbf{G }\mathbf{B }_{0})^{-1}(\mu _1+D_1\Vert \mathbf{G }\mathrm{e}^{-\mathbf{A }\tau }\Vert \Vert \bar{\mathbf{Y }}(t)\Vert ) \cdot \mathrm{sgn}(\varvec{\digamma }_1(\mathrm{e}^{-\mathbf{A }\tau }\bar{\mathbf{Y }}(t))), \end{aligned}$$

and \(\bar{\mathbf{Y }}(t)\) is the predictor state of \(\mathbf{Y }(t)\) defined by

$$\begin{aligned} \bar{\mathbf{Y }}(t):=\mathrm{e}^{\mathbf{A }\tau }\mathbf{Y }(t-\tau )+\int _{t-\tau }^{t}\mathrm{e}^{\mathbf{A }(t-\rho )}[\mathbf{B }u_2(\rho -\tau )+\varvec{\eta }_1(\rho )]\mathrm{d}\rho . \end{aligned}$$
(38)

Similarly, for Eq. (7), assume that there is a constant \(D_2\) satisfying

$$\begin{aligned} \Vert \sigma _2(t)\Vert \le D_2, \end{aligned}$$
(39)

and define the sliding mode function as

$$\begin{aligned} \digamma _2(\omega (t)):={\hat{g}}[\omega (t)-\omega (0)]-{\hat{g}}\int _0^{t}\dot{{\tilde{\omega }}}(\rho )\mathrm{d}\rho , \end{aligned}$$

where \({\hat{g}}\ne 0\) is a constant, \({\tilde{\omega }}\) is the tracking target. Then, the delayed robust control of system (7) is designed by

$$\begin{aligned} u_1(t-\tau )=u_{10}(t-\tau )+u_{11}(t-\tau ),\quad t\in [\tau ,t_f], \end{aligned}$$
(40)

where \(u_{10}(t-\tau )=\frac{\dot{{\tilde{\omega }}}}{B_2}\) is an open-loop control,

$$\begin{aligned} u_{11}(t-\tau )=-({\hat{g}}B_{2})^{-1}(\mu _2+{\hat{g}} D_{2}|{\tilde{\omega }}-{\bar{\omega }}|) \cdot \mathrm{sgn}(\digamma _2({\bar{\omega }}(t))), \end{aligned}$$

and \(B_2=\frac{rd}{\varOmega +2Ml^2 r^2}\), \({\bar{\omega }}(t)\) is the predictor state of \(\omega (t)\) defined by

$$\begin{aligned} {\bar{\omega }}(t):=\omega (t-\tau )+\int _{t-\tau }^{t}B_{2}u_1(\rho -\tau )\mathrm{d}\rho . \end{aligned}$$

The existence of the sliding mode motion and the accessibility within finite time of the sliding mode manifold can be proved in a similar way as in [27].

The optimal state of system (32) and the open-loop state of system (5) actuated by the open control \(u_{10}(t-\tau )\) are the optimal states for implementing the original turning motion task. The linearization errors and system uncertainties are dealt with using the switched control parts \(u_{21}(t-\tau )\) and \(u_{11}(t-\tau )\). Thus, the original turning motion control problem of the TWIP can be well implemented by using the proposed control method from a theoretical perspective.

In summary, the controller for the turning motion of a TWIP can be designed as follows.

Theorem 4.2

Let \(\varGamma (t)=(x_o(s),y_o(s)),~s\in [0,l]\) be a given smooth trajectory curve in the plane, in order to compel the TWIP move along the given trajectory curve, the delayed controller \((u_2(t-\tau ),~u_1(t-\tau ))\) can be designed by Eqs. (37) and (40), where \(k_{o}(s)\) is the relative curvature of \(\varGamma (s)\),

$$\begin{aligned} {\tilde{v}}={\dot{\phi }}(t), ~ {\tilde{\omega }}=k_{o}(\phi (t))({\bar{y}}_4+{\tilde{v}}), \end{aligned}$$
(41)

where \(\beta \) is a parameter to satisfy (26) for a given \(\varepsilon >0\), \({\bar{y}}_4\) is the fourth variable in the predictor state \(\bar{\mathbf{Y }}(t)\), and \(\phi (t)=-(\beta t+1)l \mathrm{e}^{-\beta t}+l\) is the one given in Lemma 3.1.

5 An Illustrative Example

In this section, numerical simulation is made for fixed parameter values and initial values: \(M=3\,\mathrm{kg},~M_\mathrm{w}=2\,\mathrm{kg},~~~~ I_\mathrm{B}=1\,\mathrm{kg\,m}^2,~I_\mathrm{w}=0.01\,\mathrm{kg\,m}^2, ~ I_z=0.01\,\mathrm{kg\,m}^2,~I_\mathrm{wd}=0.005\,\mathrm{kg\,m}^2,~l=0.5\,\mathrm{m}, ~r=0.1\,\mathrm{m},~d=0.2\,\mathrm{m},~g=9.8\,\mathrm{m/s}^2, \tau =0.01\,\mathrm{s}, ~ \mathbf{R }=1,~ \mathbf{Q }_{0}=\mathbf{0 }, ~\mathbf{Q }_{1}=\mathrm{diag}(10000,0,100,100),~ \varphi (0)=0,~ {\dot{\varphi }}(0)=0,~x(0)=0,~v(0)=0,~\omega (0)=0.\) The matrices \(\mathbf{A }\) and \(\mathbf{B }\) in system (22) become

$$\begin{aligned} \mathbf{A }=\left[ \begin{array}{cccc} 0&{}\quad 1&{}\quad 0 &{}\quad 0\\ 11.194&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ -1.8657&{}\quad 0&{}\quad 0&{}\quad 0 \end{array} \right] , \quad \quad \mathbf{B }=\left[ \begin{array}{c} 0 \\ -1.9900 \\ 0 \\ 1.5755\\ \end{array} \right] , \end{aligned}$$

and system (7) becomes \({\dot{\omega }}=-12.5u_{1}(t-\tau )+\sigma _2(t)\).

Let the task pathway be a circle defined by \(\varGamma (s)=(\mathrm{cos}s,~\mathrm{sin}s)\) for \(s\in [0,2\pi ]\). According to Sect. 4.1, with \(\beta =\frac{1}{2}\), the trajectory tracking target is given by

$$\begin{aligned} {\tilde{v}}=\frac{\pi }{2} t \mathrm{e}^{-\frac{1}{2}t}, \quad {\tilde{\omega }}=k_{o}(t)({\bar{y}}_4+{\tilde{v}}), \quad t\in [0,~+\infty [, \end{aligned}$$

and the trajectory tracking target vector of system (22) is \(\tilde{\mathbf{X }}=[0,0,{\tilde{x}},{\tilde{v}}]^{\mathrm{T}},\) where \({\tilde{x}}=-(2\pi +\pi t) \mathrm{e}^{-\frac{1}{2}t}+2\pi \). Note that the time interval of the trajectory tracking target is converted to \([0,~+\infty [\), and the corresponding Riccati differential equation (34) becomes an algebra Riccati equation of the form

$$\begin{aligned} \mathbf{0 }=-\mathbf{P }_{z}\mathbf{A }-\mathbf{A }^\mathrm{T}\mathbf{P }_z+\mathbf{P }_{z}\mathbf{B }_0\mathbf{R }^{-1}\mathbf{B }_0^\mathrm{T}\mathbf{P }_z-\tilde{\mathbf{Q }}_{1}. \end{aligned}$$
(42)

The MATLAB command lqr or MAPLE command CARE returns the solutions of (42) and (35) as follows

$$\begin{aligned}&\mathbf{P }_z=\left[ \begin{array}{cccc} 2096.1&{}\quad 530.04&{}\quad 325.74&{}\quad 557.30\\ 530.04&{}\quad 264.72&{}\quad 157.49&{}\quad 308.74 \\ 325.74&{}\quad 157.49&{}\quad 218.43&{}\quad 190.74\\ 557.30&{}\quad 308.74&{}\quad 190.74&{}\quad 371.60 \\ \end{array} \right] , \quad \\&\quad \mathbf{b }_z(t-\tau )=\left[ \begin{array}{c} (219.13t-353.60)\mathrm{e}^{-0.5t} \\ (149.59t-224.08)\mathrm{e}^{-0.5t} \\ (59.454t-120.77)\mathrm{e}^{-0.5t} \\ (178.76t-267.51)\mathrm{e}^{-0.5t} \end{array} \right] . \end{aligned}$$
Fig. 3
figure 3

Tilt angle of the pendulum

Full size image
Fig. 4
figure 4

The forward speed tracking error of the TWIP

Full size image
Fig. 5
figure 5

The yaw rotational speed of the TWIP

Full size image
Fig. 6
figure 6

The actual motion trajectory of the TWIP under the proposed controller

Full size image

In the application of the proposed controller (37) and (40) for TWIP system with strong nonlinearity and an input delay, note that the main part of \(\varvec{\sigma }_1(t)\) and \(\sigma _2(t)\) is the overall errors between the linearized nominal system and the original system (3), and thus, from the linearized system (22) and (7), one has

$$\begin{aligned}&\varvec{\sigma }_1(t)=[0,E_2,~0,~E_4]^{\mathrm{T}},\\&\sigma _2=\frac{2Mr^2 l^2{\dot{\theta }}{\dot{\varphi }}\mathrm{sin}2\varphi }{\varOmega +2Ml^2 r^2}=-18.75\omega {\dot{\varphi }}\mathrm{sin}\varphi \mathrm{cos}\varphi , \end{aligned}$$

where

$$\begin{aligned} E_2&=\frac{1}{\varDelta +M^2 l^2 r^2}\left[ -Ml(\omega ^2 l\mathrm{cos}\varphi +g)(Mr^2\mathrm{sin}\varphi +2I_\mathrm{w} \mathrm{sin}\varphi \right. \\&\quad \left. +\,2M_\mathrm{w} r^2\mathrm{sin}\varphi )+M^2 l^2r^2 {\dot{\varphi }}^2 \mathrm{sin}\varphi \mathrm{cos}\varphi \right. \\&\quad \left. +\, Mlg(Mr^2 \varphi +2I_\mathrm{w}\varphi +2M_\mathrm{w} r^2\varphi )+Mlr(\mathrm{cos}\varphi -1)u_2(t-\tau )\right] \\&=0.5597\omega ^2\mathrm{sin}\varphi \mathrm{cos}\varphi +11.194\mathrm{sin}\varphi -0.1866{\dot{\varphi }}^2\mathrm{sin}\varphi \mathrm{cos}\varphi \\&\quad -\, 11.194\varphi -1.2438\mathrm{cos}\varphi u_2(t-\tau )+1.2438u_2(t-\tau ), \end{aligned}$$
$$\begin{aligned} E_4&=\frac{1}{\varDelta +M^2 l^2 r^2}\left[ M^2 l^2 r^2\mathrm{sin}\varphi \mathrm{cos}\varphi (\omega ^2 l\mathrm{cos}\varphi +g)-M^2 l^3 r^2{\dot{\varphi }}^2\mathrm{sin}\varphi \right. \\&\quad \left. -\,I_\mathrm{B} M l r^2 {\dot{\varphi }}^2\mathrm{sin}\varphi -\, M^2 l^2 r^2 \varphi g-Mlr^2(\mathrm{cos}\varphi -1)u_2(t-\tau )\right] \\&=-0.0933\omega ^2\mathrm{sin}\varphi \mathrm{cos}^2 \varphi -\, 1.8657\mathrm{sin}\varphi \mathrm{cos}\varphi +0.2177{\dot{\varphi }}^2\mathrm{sin}\varphi \\&\quad +1.8657\varphi +0.1244\mathrm{cos}\varphi u_2(t-\tau )-\, 0.1244u_2(t-\tau ). \end{aligned}$$

Moreover, let \(\mathbf{G }=[0,1,0,1.8978],~{\hat{g}}=-\frac{1}{12.5}\),  \(\mu _1=\mu _2=0.1,~D_1=D_2=0.51\), used in the above switched control. Then, all the quantities required in the delayed trajectory tracking controller (37) and (40) are available in hand. Now, the time histories of all the state variables can be simulated.

Figure 3 shows that the tilt angle of the pendulum becomes small enough and is stabilized after a short transient. Figures 4 and 5 present the time history of the tracking error of the forward speed and the yaw rotational speed, respectively. Figure 6 shows that the actual motion trajectory is extremely closed to the target trajectory curve, when the dynamical tracking target \({\tilde{\omega }}=k_o(t)v(t)\) is applied, and the location error is very large if the rotational speed target is chosen as a nondynamic target \({\tilde{\omega }}=\frac{{\dot{x}}_{o}\ddot{y}_{o}-\ddot{x}_{o}{\dot{y}}_{o}}{{\dot{x}}_{o}^2+{\dot{y}}_{o}^2}\). The so-called nondynamic target is pre-designed by using the pre-determined trajectory curve, which cannot be varied with the state variable. In this case, the cumulative error becomes larger and larger and cannot be reduced. The simulation results indicate that a given turning motion task of the TWIP is well achieved by using the proposed control method, and the vibration amplitudes of the state variables would be magnified obviously if the small input delay is ignored in designing controllers.

6 Conclusions

A special feature of this paper is the application of the theory of planar curve in designing the controller. Two major points can be deduced from the proposed control design. One is that in order to keep the TWIP walking along the target trajectory curve accurately, it is important to have the curvature of the target trajectory curve well tracked. Thus, the product of the curvature of the target curve and the forward speed of the TWIP is chosen as a dynamic yaw rotational target. When the dynamical yaw rotational target is designed in such a way, the tracking error of the position can be greatly reduced compared with the use of nondynamical tracking target. The other is that there are almost no limits to the forward speed target if one does not mind the amount of the motion speed in the whole motion process. The use of the forward speed as a target enables that the accumulative error caused by the initial speed error can be reduced dramatically, and the LQR-based optimal trajectory controller is easily determined simply by solving Riccati algebraic equations. Numerical simulations show that with the designed controller, not only the given trajectory curve is well tracked, but also the inverted pendulum is well stabilized.