Skip to main content
SpringerLink
Log in

Span Observables: “When is a Foraging Rabbit No Longer Hungry?”

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

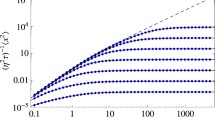
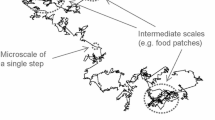
Be \(X_t\) a random walk. We study its span S, i.e. the size of the domain visited up to time t. We want to know the probability that S reaches 1 for the first time, as well as the density of the span given t. Analytical results are presented, and checked against numerical simulations. We then generalize this to include drift, and one or two reflecting boundaries. We also derive the joint probability of the maximum and minimum of a process. Our results are based on the diffusion propagator with reflecting or absorbing boundaries, for which a set of useful formulas is derived.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Feller, W.: Introduction to Probability Theory and Its Applications. Wiley, New York (1950)

    MATH  Google Scholar 

  2. Redner, S.: A Guide to First-Passage Problems. Cambridge University Press, Cambridge (2001)

    Book  Google Scholar 

  3. Borodin, A.N., Salminen, P.: Handbook of Brownian Motion—Facts and Formulae. Birkhäuser, Boston (2002)

    Book  Google Scholar 

  4. Weiss, G.H., DiMarzio, E.A., Gaylord, R.J.: First passage time densities for random walk spans. J. Stat. Phys. 42, 567–572 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  5. Palleschi, V., Torquati, M.R.: Mean first-passage time for random-walk span: comparison between theory and numerical experiment. Phys. Rev. A 40, 4685–4689 (1989)

    Article  ADS  Google Scholar 

  6. Daniels, H.E.: The probability distribution of the extent of a random chain. Math. Proc. Camb. Philos. Soc. 37, 244–251 (1941)

    Article  ADS  MathSciNet  Google Scholar 

  7. Feller, W.: The asymptotic distribution of the range of sums of independent random variables. Ann. Math. Stat. 22, 427–432 (1951)

    Article  MathSciNet  Google Scholar 

  8. Weiss, G.H., Rubin, R.J.: The theory of ordered spans of unrestricted random walks. J. Stat. Phys. 14, 333–350 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  9. Annesi, B., Marinari, E., Oshanin, G.: Covariance of the running range of a Brownian trajectory, (2019), arXiv:1902.06963

    Article  MathSciNet  Google Scholar 

  10. Rager, C.L., Bhat, U., Bénichou, O., Redner, S.: The advantage of foraging myopically. J. Stat. Mech. 2018, 073501 (2018)

    Article  MathSciNet  Google Scholar 

  11. Cannon, J.R.: The One-Dimensional Heat Equation. Encyclopedia of Mathematics and Its Applications, vol. 23. Department of Mathematics, MIT, Cambridge (1984)

    Book  Google Scholar 

  12. Bray, A.J., Smith, R.: Survival probability of a diffusing particle constrained by two moving, absorbing boundaries. J. Phys. A 40, F235 (2007). cond-mat/0612563

    Article  ADS  MathSciNet  Google Scholar 

  13. Wiese, K.J.: First passage in an interval for fractional Brownian motion. Phys. Rev. E 99 032106, (2018) arXiv:1807.08807

  14. Wergen, G., Bogner, M., Krug, J.: Record statistics for biased random walks, with an application to financial data, Phys. Rev. E 83 051109, (2011) arXiv:1103.0893

  15. Mirny, L., Slutsky, M., Wunderlich, Z., Tafvizi, A., Leith, J., Kosmrlj, A.: How a protein searches for its site on DNA: the mechanism of facilitated diffusion. J. Phys. A 42, 434013 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  16. Nourdin, I.: Selected Aspects of Fractional Brownian Motion. Bocconi & Springer Series, New York (2012)

    Book  Google Scholar 

  17. Dieker, A.B.: Simulation of fractional Brownian motion, www.columbia.edu/~ad3217/fbm/thesis.pdf PhD thesis, University of Twente, (2004)

  18. Krug, J.: Persistence of non-Markovian processes related to fractional Brownian motion. Markov Process. Relat. Fields 4, 509–516 (1998)

    MathSciNet  MATH  Google Scholar 

  19. Sadhu, T., Delorme, M., Wiese, K.J.: Generalized arcsine laws for fractional Brownian motion. Phys. Rev. Lett. 120, 040603 (2018). https://doi.org/10.1103/PhysRevLett.120.040603

    Article  ADS  MathSciNet  Google Scholar 

  20. Salminen, P., Vallois, P.: On maximum increase and decrease of Brownian motion. Ann. Inst. Henri Poincaré PR 43, 655–676 (2007)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

After completion of this work we learned that for the drift-free case the time that the span first reaches one was already calculated in Phys. Rev. E 94, 062131 (2016).

Author information

Authors and Affiliations

  1. Laboratoire de Physique de l’Ecole Normale Supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université Paris-Diderot, Sorbonne Paris Cité, Paris, France

    Kay Jörg Wiese

Authors
  1. Kay Jörg Wiese
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kay Jörg Wiese.

Additional information

Communicated by Giulio Biroli.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wiese, K.J. Span Observables: “When is a Foraging Rabbit No Longer Hungry?”. J Stat Phys 178, 625–643 (2020). https://doi.org/10.1007/s10955-019-02446-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-019-02446-6

Keywords

Search

Navigation