How drug onset rate and duration of action affect drug forgiveness

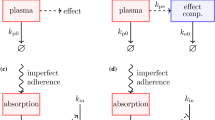
Abstract

Medication nonadherence is one of the largest problems in healthcare today, particularly for patients undergoing long-term pharmacotherapy. To combat nonadherence, it is often recommended to prescribe so-called “forgiving” drugs, which maintain their effect despite lapses in patient adherence. Nevertheless, drug forgiveness is difficult to quantify and compare between different drugs. In this paper, we construct and analyze a stochastic pharmacokinetic/pharmacodynamic (PK/PD) model to quantify and understand drug forgiveness. The model parameterizes a medication merely by an effective rate of onset of effect when the medication is taken (on-rate) and an effective rate of loss of effect when a dose is missed (off-rate). Patient dosing is modeled by a stochastic process that allows for correlations in missed doses. We analyze this “on/off” model and derive explicit formulas that show how treatment efficacy depends on drug parameters and patient adherence. As a case study, we compare the effects of nonadherence on the efficacy of various antihypertensive medications. Our analysis shows how different drugs can have identical efficacies under perfect adherence, but vastly different efficacies for adherence patterns typical of actual patients. We further demonstrate that complex PK/PD models can indeed be parameterized in terms of effective on-rates and off-rates. Finally, we have created an online app to allow pharmacometricians to explore the implications of our model and analysis.

Appendix

In this Appendix, we collect details of the mathematical analysis.

Moments of drug effect

We now compute the first and second moments in (7)–(8). First, for the transition probabilities in (4)–(5), the transition matrix is

$$\begin{aligned} P = \begin{pmatrix} p_0 &{} 1-p_0 \\ 1-p_1 &{} p_1 \end{pmatrix}, \end{aligned}$$

(20)

and the stationary distribution is

$$\begin{aligned} \pi = \begin{pmatrix} \displaystyle {\frac{1-p_1}{2-p_0-p_1}}&\displaystyle {\frac{1-p_0}{2-p_0-p_1}} \end{pmatrix}. \end{aligned}$$

Hence, the proportion of doses taken is

$$\begin{aligned} p = \pi (1) = \frac{1-p_0}{2-p_0-p_1}. \end{aligned}$$

Note that the first moment of X is given by the sum

$$\begin{aligned} {\mathbb {E}}[X_{0}] = {\mathbb {E}}[X_{0}\mathbbm {1}_{\xi _{-1}=0}] + {\mathbb {E}}[X_{0}\mathbbm {1}_{\xi _{-1}=1}], \end{aligned}$$

where $\mathbbm {1}_{E}\in \{0,1\}$ denotes the indicator function, which takes on a value of 1 if the event E occurs and 0 otherwise. At steady state (i.e. the patient has been taking the medication for sufficiently long at adherence rate p), we have

$$\begin{aligned} X {\mathop {=}\limits ^{\text {d}}}\alpha X + (\beta -\alpha )X\xi + (1-\beta )\xi , \end{aligned}$$

(21)

where $X{\mathop {=}\limits ^{\text {d}}}Y$ denotes equality in distribution. Therefore,

$$\begin{aligned} X_{0} {\mathop {=}\limits ^{\text {d}}}X_{1} = \alpha X_0 + (\beta -\alpha )X_0\xi _1 + (1-\beta )\xi _1, \end{aligned}$$

which means that

$$\begin{aligned} X_{0}\mathbbm {1}_{\xi _0=j} {\mathop {=}\limits ^{\text {d}}}X_{1}\mathbbm {1}_{\xi _1=j} = \left( \alpha X_0 + (\beta -\alpha )X_0\xi _1 + (1-\beta )\xi _1\right) \mathbbm {1}_{\xi _1=j}. \end{aligned}$$

Taking the expected value, we have

$$\begin{aligned} {\mathbb {E}}[X_{0}\mathbbm {1}_{\xi _0=j}]&= {\mathbb {E}}[X_{1}\mathbbm {1}_{\xi _1=j}] \nonumber \\&= {\left\{ \begin{array}{ll} {\mathbb {E}}[\alpha X_{0}\mathbbm {1}_{\xi _1=0}], &{} j=0, \\ {\mathbb {E}}[\left( \beta X_{0} + (1-\beta )\right) \mathbbm {1}_{\xi _1=1}], &{} j=1, \end{array}\right. } \nonumber \\&= {\left\{ \begin{array}{ll} \alpha {\mathbb {E}}[X_{0}\mathbbm {1}_{\xi _1=0}], &{} j=0, \\ (1-\beta )\pi (1) + \beta {\mathbb {E}}[X_{0}\mathbbm {1}_{\xi _1=1}], &{} j=1. \end{array}\right. }, \end{aligned}$$

(22)

where $\pi (1) = p$. Note that

$$\begin{aligned} {\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=j}]&= \sum _{i=0}^{1}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=j}\mathbbm {1}_{\xi _0=i}] \nonumber \\&= \sum _{i=0}^{1}{\mathbb {E}}[{\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=j}\mathbbm {1}_{\xi _0=i}\,|\,\{\xi _n\}_{n\le -1}]], \end{aligned}$$

(23)

where the second equality comes from the tower property of conditional expectation. The term within the sum can be simplified. For a function $f(X_{0},j)$,

$$\begin{aligned}&{\mathbb {E}}[{\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _1=j}\mathbbm {1}_{\xi _0=i}\,|\,\{\xi _n\}_{n\le -1}]]\nonumber \\&\quad = {\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _0=i}{\mathbb {E}}[\mathbbm {1}_{\xi _1=j}\,|\,\{\xi _n\}_{n\le -1}]] \nonumber \\&\quad = {\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _0=i}P_{ij}] \nonumber \\&\quad = P_{ij}{\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _0=i}], \end{aligned}$$

(24)

where $P_{ij}$ is the ij-th entry of the transition matrix (20). This means that

$$\begin{aligned} {\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _1=j}]&= \sum _{i=0}^{1}P_{ij}{\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _0=i}] \\&= P_{0j}{\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _0=0}] \\&\quad + P_{1j}{\mathbb {E}}[f(X_0,j)\mathbbm {1}_{\xi _0=1}]. \end{aligned}$$

Combining this result with (22) we have

$$\begin{aligned} {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}]&= {\mathbb {E}}[X_1\mathbbm {1}_{\xi _1=0}] = \alpha {\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=0}] \\&= \alpha \left( P_{00}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}] + P_{10}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}]\right) , \\ {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}]&= {\mathbb {E}}[X_1\mathbbm {1}_{\xi _1=1}] = (1-\beta )\pi (1) + \beta {\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=1}] \\&= (1-\beta )\pi (1) + \beta \left( P_{01}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}] \right. \\&\left. \quad + P_{11}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}]\right) . \end{aligned}$$

These lead to the system of equations

$$\begin{aligned} {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}]&= \frac{\alpha (1-p_1)}{1-\alpha p_0}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}], \\ {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}]&= \frac{(1-\beta )\pi (1)}{1-\beta p_1} + \frac{\beta (1-p_0)}{1-\beta p_1}{\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}]. \end{aligned}$$

The solution to this system is

$$\begin{aligned} {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}]&= \frac{\pi (1)\alpha (1-\beta )(1-p_1)}{(1-\beta p_1)(1-\alpha p_0)-\alpha \beta (1-p_0)(1-p_1)}, \\ {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}]&= \frac{\pi (1)(1-\beta )(1-\alpha p_0)}{(1-\beta p_1)(1-\alpha p_0)-\alpha \beta (1-p_0)(1-p_1)}. \end{aligned}$$

Thus,

$$\begin{aligned} {\mathbb {E}}[X_0]&= {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=0}] + {\mathbb {E}}[X_0\mathbbm {1}_{\xi _0=1}] \\&= \frac{\pi (1)(1-\beta )\left( \alpha (1-p_1)+(1-\alpha p_0)\right) }{(1-\beta p_1)(1-\alpha p_0)-\alpha \beta (1-p_0)(1-p_1)}. \end{aligned}$$

The second moment can be computed in a similar fashion. Note that

$$\begin{aligned} X_{0}^2 {\mathop {=}\limits ^{\text {d}}}X_{1}^2 = \left( \alpha X_0 + (\beta -\alpha )X_0\xi _1 + (1-\beta )\xi _1\right) ^2, \end{aligned}$$

and thus

$$\begin{aligned} {\mathbb {E}}[X_{0}^2\mathbbm {1}_{\xi _0=j}]&= {\mathbb {E}}[X_{1}^2\mathbbm {1}_{\xi _1=j}] \nonumber \\&= {\left\{ \begin{array}{ll} {\mathbb {E}}[\alpha ^2 X_{0}^2\mathbbm {1}_{\xi _1=0}], &{} j=0, \\ {\mathbb {E}}[\left( \beta X_{0} + (1-\beta )\right) ^2\mathbbm {1}_{\xi _1=1}], &{} j=1, \end{array}\right. } \end{aligned}$$

(25)

The results in (23) and (24) can be applied to ${\mathbb {E}}[X_{0}^2\mathbbm {1}_{\xi _1=j}]$, which gives

$$\begin{aligned} {\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=j}]&= P_{0j}{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _0=0}] + P_{1j}{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _0=1}] \end{aligned}$$

Thus,

$$\begin{aligned} {\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=0}]&= {\mathbb {E}}[X_1^2\mathbbm {1}_{\xi _2=0}] = \alpha ^2{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _2=0}] \\&= \alpha ^2\left( P_{00}{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=0}] + P_{10}{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=1}]\right) \\&= \alpha ^2\left( p_0{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=0}] + (1-p_1){\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=1}]\right) , \\ {\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=1}]&= {\mathbb {E}}[X_1^2\mathbbm {1}_{\xi _2=1}] \\&= (1-\beta )^2\pi (1) + 2\beta (1-\beta ){\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=1}] \\&\quad + \beta ^2{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _2=1}] \\&= (1-\beta )^2\pi (1) + 2\beta (1-\beta ){\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=1}] \\&\quad + \beta ^2\left( (1-p_0){\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=0}] + p_1{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=1}]\right) . \end{aligned}$$

From this system of equations we have

$$\begin{aligned}&{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=0}] \\&\quad = \left( \frac{\alpha ^2(1-p_1)}{(1-\alpha ^2p_0)(1-\beta ^2p_1)-\alpha ^2\beta ^2(1-p_0)(1-p_1)}\right) \\&\qquad \times \left( (1-\beta )^2\pi (1) + 2\beta (1-\beta ){\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=1}]\right) , \\&{\mathbb {E}}[X_0^2\mathbbm {1}_{\xi _1=0}] \\&\quad = \left( \frac{(1-\alpha ^2p_0)}{(1-\alpha ^2p_0)(1-\beta ^2p_1)-\alpha ^2\beta ^2(1-p_0)(1-p_1)}\right) \\&\qquad \times \left( (1-\beta )^2\pi (1) + 2\beta (1-\beta ){\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=1}]\right) , \end{aligned}$$

which means that the second moment is

$$\begin{aligned} {\mathbb {E}}[X_0^2]&= \left( \frac{\alpha ^2(1-p_1)+(1-\alpha ^2p_0)}{(1-\alpha ^2p_0)(1-\beta ^2p_1)-\alpha ^2\beta ^2(1-p_0)(1-p_1)}\right) \\&\qquad \qquad \times \left( (1-\beta )^2\pi (1) + 2\beta (1-\beta ){\mathbb {E}}[X_0\mathbbm {1}_{\xi _1=1}]\right) . \end{aligned}$$

Numerical computation of ${\mathbb {P}}(X>\theta )$

Assuming independence of $\{\xi _{n}\}_{n\in {\mathbb {Z}}}$, the distribution function of the biomarker response level can be numerically computed using the recursion relationship (3). By (21), we have that

$$\begin{aligned} {\mathbb {P}}(X_{n} \le x)&= {\mathbb {P}}(\alpha X_{n} + (\beta -\alpha )X_{n}\xi _{n+1} + (1-\beta )\xi _{n+1} \le x) \\&= (1-p){\mathbb {P}}(X_{n} \le x/\alpha ) + p{\mathbb {P}}(X_{n} \le (x-1)/\beta + 1). \end{aligned}$$

Denoting the distribution function of X by $F(x) = {\mathbb {P}}(X \le x)$, we thus have

$$\begin{aligned} F(x) = (1-p)F\left( \frac{x}{\alpha }\right) + pF\left( \frac{x-1}{\beta } + 1\right) . \end{aligned}$$

(26)

By starting with an initial guess for the distribution function of X and iteratively applying (26), the true distribution function of X can be numerically determined. Specifically, we obtain a sequence of approximating distribution functions $\{F_{m}(x)\}_{m\ge 0}$ where $F_{0}(x)=x$ and $F_{m+1}(x)$ is defined by $F_{m}(x)$ via

$$\begin{aligned} F_{m+1}(x) = (1-p)F_{m}\left( \frac{x}{\alpha }\right) + pF_{m}\left( \frac{x-1}{\beta } + 1\right) . \end{aligned}$$

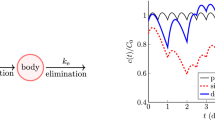
The dashed curves in Fig. 4 are obtained via this recursion once successive iterations $F_{m}(x)$ and $F_{m+1}(x)$ differ by less than $10^{-10}$ for all $x\in [0,1]$.

Beta distribution formulas

In the "Mean and variance of biomarker response" section, we described how we can approximate the full probability distribution of X by a Beta random variable B chosen so that the first and second moments of X and B agree. We now give the explicit formulas for this Beta distribution fit.

The probability density function of a Beta random variable B is given by

$$\begin{aligned} f_{B}(x) =\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}x^{a-1}(1-x)^{b-1},\quad \text {if }x\in (0,1), \end{aligned}$$

and $f_{B}(x)=0$ for $x\notin (0,1)$, where $\Gamma (z)=\int _{0}^{\infty }u^{z-1}e^{-u}\,\text {d} u$ denotes the Gamma function. The first and second moments of B are

$$\begin{aligned} {\mathbb {E}}[B] = \frac{a}{a+b}, \quad {\mathbb {E}}[B^2] = \frac{a(a+1)}{(a+b)(a+b+1)}. \end{aligned}$$

Therefore, choosing a and b so that ${\mathbb {E}}[B]={\mathbb {E}}[X]$ and ${\mathbb {E}}[B^{2}]={\mathbb {E}}[X^{2}]$ implies

$$\begin{aligned} a =\frac{{\mathbb {E}}[X]({\mathbb {E}}[X]-{\mathbb {E}}[X^{2}])}{{\mathbb {E}}[X^{2}]-({\mathbb {E}}[X])^{2}},\quad b =\frac{(1-{\mathbb {E}}[X])({\mathbb {E}}[X]-{\mathbb {E}}[X^{2}])}{{\mathbb {E}}[X^{2}]-({\mathbb {E}}[X])^{2}}. \end{aligned}$$

(27)