Extreme Learning Machine Framework for Risk Stratification of Fatty Liver Disease Using Ultrasound Tissue Characterization

Abstract

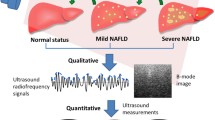
Fatty Liver Disease (FLD) is caused by the deposition of fat in liver cells and leads to deadly diseases such as liver cancer. Several FLD detection and characterization systems using machine learning (ML) based on Support Vector Machines (SVM) have been applied. These ML systems utilize large number of ultrasonic grayscale features, pooling strategy for selecting the best features and several combinations of training/testing. As result, they are computationally intensive, slow and do not guarantee high performance due to mismatch between grayscale features and classifier type. This study proposes a reliable and fast Extreme Learning Machine (ELM)-based tissue characterization system (a class of Symtosis) for risk stratification of ultrasound liver images. ELM is used to train single layer feed forward neural network (SLFFNN). The input-to-hidden layer weights are randomly generated reducing computational cost. The only weights to be trained are hidden-to-output layer which is done in a single pass (without any iteration) making ELM faster than conventional ML methods. Adapting four types of K-fold cross-validation (K = 2, 3, 5 and 10) protocols on three kinds of data sizes: S0-original, S4-four splits, S8-sixty four splits (a total of 12 cases) and 46 types of grayscale features, we stratify the FLD US images using ELM and benchmark against SVM. Using the US liver database of 63 patients (27 normal/36 abnormal), our results demonstrate superior performance of ELM compared to SVM, for all cross-validation protocols (K2, K3, K5 and K10) and all types of US data sets (S0, S4, and S8) in terms of sensitivity, specificity, accuracy and area under the curve (AUC). Using the K10 cross-validation protocol on S8 data set, ELM showed an accuracy of 96.75% compared to 89.01% for SVM, and correspondingly, the AUC: 0.97 and 0.91, respectively. Further experiments also showed the mean reliability of 99% for ELM classifier, along with the mean speed improvement of 40% using ELM against SVM. We validated the symtosis system using two class biometric facial public data demonstrating an accuracy of 100%.

Appendices

Appendix A: ELM mathematical framework and solution

Let there be H hidden layer neurons and N output neurons. Let each training sample of P images be denoted as (a _j , l _j ), where each input image denoted as a _j  = [a _j1, a _j2, …, a _jm ]^T ∈ R ^m and each output label is denoted as l _j  = [l _j1,  l _j2, …, l _jN ]^T ∈ R ^N. The output vector is denoted as L = [l ₁,  l ₂, …, l _j , …l _P ]^T. Further, the P images and their ground truth labels are divided into two parts for training and testing which can be represented by ${\boldsymbol{P}}_{trg}=\left({\boldsymbol{a}}_j^{trg},{\boldsymbol{l}}_j^{trg}\right)$ for training and ${\boldsymbol{P}}_{tst}=\left({\boldsymbol{a}}_k^{tst},{\boldsymbol{l}}_k^{tst}\right)$. Similarly, output vector L is also divided into two sets L _trg and L _tst . Each input layer neuron is connected to all hidden layer neurons. Let each hidden layer weight be denoted as a vector w _i  = [w _1i ,  w _2i , …, w _mi  ]^T. Each of the connections or weights from hidden-to-output layer are denoted as δ _i  = [δ _i1,  δ _i2, …,  δ _iN ]^T connecting i ^th hidden node to the output nodes. A standard SLFFNN can be modeled as given by:

$$ {\sum}_{i=1}^H{\boldsymbol{\delta}}_{\boldsymbol{i}}\ {g}_i\left({\boldsymbol{a}}_{\boldsymbol{j}}^{\boldsymbol{trg}}\right)={\sum}_{i=1}^H{\boldsymbol{\delta}}_{\boldsymbol{i}}\ g\left({\boldsymbol{w}}_{\boldsymbol{i}}{\boldsymbol{a}}_{\boldsymbol{j}}^{\boldsymbol{trg}}+{b}_i\right)={\boldsymbol{l}}_{\boldsymbol{j}}^{\boldsymbol{trg}}\kern2.75em for\ j=1,2,\dots, \#{\boldsymbol{P}}_{\boldsymbol{trg}}\Big) $$

(4)

where, g is the activation function and b is the bias. This equation is written in more compact form which is given by:

$$ \boldsymbol{Q}\boldsymbol{\delta } ={\boldsymbol{L}}_{\boldsymbol{trg}} $$

(5)

where,

$$ \boldsymbol{Q}\left({w}_1,\dots, {w}_H,\kern0.5em {b}_1,\dots, {b}_H,{\boldsymbol{a}}_1^{trg},\dots, {\boldsymbol{a}}_P^{trg}\right)={\left[\begin{array}{ccc}\hfill g\left({w}_1.{\boldsymbol{a}}_1^{trg}+{b}_1\right)\hfill & \hfill \dots \kern0.5em g\left({w}_i.{\boldsymbol{a}}_1^{trg}+{b}_i\right)\kern0.5em \dots \hfill & \hfill g\left({w}_H.{\boldsymbol{a}}_1^{trg}+{b}_H\right)\hfill \\ {}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill g\left({w}_1.{\boldsymbol{a}}_j^{trg}+{b}_1\right)\hfill \\ {}\hfill \vdots \hfill \end{array}\hfill & \hfill \dots \kern0.5em \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill g\left({w}_i.{\boldsymbol{a}}_j^{trg}+{b}_i\right)\hfill \\ {}\hfill \vdots \hfill \end{array}\kern0.5em \dots \hfill & \hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill g\left({w}_H.{\boldsymbol{a}}_j^{\boldsymbol{trg}}+{b}_H\right)\hfill \\ {}\hfill \vdots \hfill \end{array}\hfill \\ {}\hfill g\left({w}_1.{\boldsymbol{a}}_P^{trg}+{b}_1\right)\hfill & \hfill \begin{array}{ccc}\hfill \dots \hfill & \hfill g\left({w}_i.{\boldsymbol{a}}_P^{trg}+{b}_i\right)\hfill & \hfill \dots \hfill \end{array}\hfill & \hfill g\left({w}_H.{\boldsymbol{a}}_P^{trg}+{b}_H\right)\hfill \end{array}\right]}_{\#{\boldsymbol{P}}_{trg}\times H} $$

$\boldsymbol{\delta} ={\left[\begin{array}{c}\hfill {\delta}_1^T\hfill \\ {}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill {\delta}_i^T\hfill \\ {}\hfill \vdots \hfill \end{array}\hfill \\ {}\hfill {\delta}_H^T\hfill \end{array}\right]}_{H\times N}\mathrm{and}\ {\boldsymbol{L}}_{trg}={\left[\begin{array}{c}\hfill {\boldsymbol{l}}_1^{trg}\hfill \\ {}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill {\boldsymbol{l}}_{\boldsymbol{j}}^{trg}\hfill \\ {}\hfill \vdots \hfill \end{array}\hfill \\ {}\hfill {\boldsymbol{l}}_{\#{\boldsymbol{P}}_{trg}}^{trg}\hfill \end{array}\right]}_{\#{\boldsymbol{P}}_{\boldsymbol{trg}}\times N}.\mathrm{The}\ \mathrm{cost}\ \mathrm{function}\ \mathrm{of}\ \mathrm{ELM}\ \mathrm{is}\ \mathrm{given}\ \mathrm{as}:$

$$ E={\sum}_{j=1}^P{\left({\sum}_{i=1}^H{\boldsymbol{\delta}}_{\boldsymbol{i}}\ g\left({w}_i{\boldsymbol{a}}_{\boldsymbol{j}}^{\boldsymbol{trg}}+{b}_i\right)-{\boldsymbol{l}}_{\boldsymbol{j}}^{\boldsymbol{trg}}\right)}^2 $$

(6)

The objective is to find the minimum δ which minimizes the cost function E. By using Eq. 5, the Eq. 6 can also be written as:

$$ \left\Vert \boldsymbol{Q}\widehat{\boldsymbol{\delta}}-{\boldsymbol{L}}_{\boldsymbol{trg}}\right\Vert =\underset{\delta }{\min}\boldsymbol{Q}\boldsymbol{\delta } -{\boldsymbol{L}}_{\boldsymbol{trg}}\Big\Vert $$

(7)

where $\hat{\boldsymbol{\delta}}$ is the least squares solution of the Qδ = L _trg . If the number of hidden nodes is equal to the number of training samples (#P _trg  = H), the matrix  Q is square and invertible. Therefore, with random weights w _i and bias b _i the training samples can be approximated with zero error. However, in maximum cases, number of training samples is larger than number of hidden nodes. So, the smallest norm least squares solution of the linear system is given by:

$$ \hat{\boldsymbol{\delta}}={\boldsymbol{Q}}^{\dagger }{\boldsymbol{L}}_{trg} $$

(8)

Where, Q ^† is the Moore–Penrose [35] generalized inverse of matrix Q. Thus the smallest training error can be reached by:

$$ \left\Vert \boldsymbol{Q}\hat{\boldsymbol{\delta}}-{\boldsymbol{L}}_{\boldsymbol{trg}}\right\Vert =\left\Vert {\boldsymbol{QQ}}^{\dagger }{\boldsymbol{L}}_{\boldsymbol{trg}}-{\boldsymbol{L}}_{\boldsymbol{trg}}\right\Vert =\underset{\delta }{\min}\left\Vert \boldsymbol{Q}\boldsymbol{\delta } -{\boldsymbol{L}}_{\boldsymbol{trg}}\right\Vert $$

(9)

The trained hidden-to-output layer weights are then used in Testing-phase as shown in Fig. 5, to test the performance of the Symtosis model using test dataset P _tst .

Appendix B: Support vector machine

Support Vector Machine (SVM) is a kernel based classification technique based on the maximum margin classifier. It transforms the original input data to high-dimensional feature space and tries to find the hyper-plane which maximizes the distance between data points of distinct classes. We consider a binary classification task with the training dataset designated as {(a _i , L _i ), i = 1, 2, …, l} where a _i є R ^q is the input data for i ^th training sample and L _i є [−1, +1] are the equivalent target values, l designates total number of samples and q is the input space dimension. The SVM model can be represented in feature space by following equation:

(10)

where, ℵ(x) represents kernel function, b represents bias and is a weight vector which is normal to the hyper-plane. The decision rule is mathematically represented in the Eq. (11):

(11)

The non-linear kernel function finds the maximum margin hyper-plane, between the classes in a feature space. To find optimal hyper-plane, the Eq. (12) is minimized subject to Eqs. (10) and (11).

(12)

where, ϑ represents the trade-off between error and margin and ξ is a slack variable. By using Lagrangian multipliers (α) in dual form, the Eq. (12) can be transformed into following optimization problem:

$$ \mathrm{maximize}\kern0.5em \sum_{i=1}^l{\alpha}_i-\frac{1}{2}\sum_{i=1}^l\sum_{j=1}^l{\alpha}_i{\alpha}_j{L}_i{L}_j{K}_f\left({a}_i,{a}_j\right)\kern0.5em $$

(13)

$$ \mathrm{subject}\ \mathrm{to}\kern0.5em \sum_{i=1}^l{\alpha}_i{L}_i=0,\kern0.75em {\alpha}_i\ge 0\forall i $$

(14)

$$ \mathrm{where},\kern0.5em {K}_f\left({a}_i,{a}_j\right)=\aleph {\left({a}_i\right)}^T.\aleph \left({a}_j\right) $$

(15)

The final decision function is given by following equation:

$$ L(x)=\sum_{i=1}^l{\alpha}_i{L}_i{K}_f\left(a,{a}_i\right)+\gamma $$

(16)

The parameters ωand γ define the separating hyperplane. The most general kernel functions are:

$$ \mathrm{Linear}\ \mathrm{Kernel}:\kern0.5em {K}_f\left(a,{a}^{\hbox{'}}\right)=a.{a}^{\hbox{'}} $$

(17)

$$ \mathrm{Polynomial}\ \mathrm{Kernel}:\kern0.5em {K}_f\left(a,{a}^{\hbox{'}}\right)={\left(a.{a}^{\hbox{'}}+1\right)}^{deg} $$

(18)

Where, deg. is the degree of kernel in Eq. 18 and (.) denotes the dot product.

Appendix C: Feature extraction

Haralick texture (GLCM)

GLCM calculates the following features shown Table 7 from the co-occurrence matrix calculated from the image.

Table 7 Features from gray level co-occurrence matrix

Run length texture

GRLM feature extraction algorithm calculate features from the run length matrix as shown in Table 8.

Table 8 Features from gray level run length matrix

Appendix D: Symbols table

Table 9 Symbols and their description

Appendix E: Results of ELM/SVM classifier for S4 and S8 dataset

Table 10 Comparison between ELM-based and SVM-based learning methods for S4 dataset

Table 11 Comparison between ELM-based and SVM-based learning methods for S8 dataset

Appendix F: Scientific validation

Scientific validation is always an integrated component of the system design. For validation, one needs to run another set of liver data sets whose results are known a priori. Since such a clinical data is hard to obtain, we use facial biometric data set to test the classification accuracy. We do acknowledge Dr. Libor Spacek of Department of Computer Science, University of Essex for providing data on biometric facial dataset, namely Face94 [42]. This dataset consisting of male and female faces was experimented for validation using ELM/SVM.

Face94 data set

We have conducted experiments to validate our results using Face94 data set. The Face94 data set consists 153 individual images with various expressions and poses seated at a fixed distance from camera. There are 2 classes, male and female and total number of images are 2660, of which 2260 are male images and 400 are female images. A subset of images is given in Fig. 10. Cross-validation protocol (K2, K3, K5 and K10) is also performed to check generalization. The validation results are shown in Table 12. It is seen ELM gives 100% accuracy across all cross-validation protocols.

Fig. 10

Male images (top row) and female images (bottom row) taken from Face94 data set

Table 12 Comparison between ELM and SVM for Face94 dataset