1 Introduction

In this paper, we investigate the existence of unbounded solutions for a system of coupled asymmetric oscillators of the type

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{x}_1+a_1x_1^+-b_1x^-_1+\phi _1(x_2)=p_1(t) \\ \ddot{x}_2+a_2\,x_2^+-b_2\,x^-_2+\phi _2(x_1)=p_2(t), \end{array} \right. \end{aligned}$$
(1.1)

where, as usual, \(x^{\pm } = \max \{\pm x,0\}\) and, for \(i=1,2\), \(\phi _i: \mathbb {R} \rightarrow \mathbb {R}\) is locally Lipschitz continuous and bounded, \(p_i: \mathbb {R} \rightarrow \mathbb {R}\) is continuous and \(2\pi \)-periodic. As for the positive real numbers \(a_i, b_i\), we assume that

$$\begin{aligned} \dfrac{1}{\sqrt{a_i}}+\dfrac{1}{\sqrt{b_i}}=\dfrac{2}{n}, \quad \text{ for } \text{ some } n \in \mathbb {N}, \end{aligned}$$
(1.2)

thus implying that each oscillator is at resonance with respect to the same curve of the Fucik spectrum [11].

The study of unbounded solutions for oscillators at resonance is a classical topic in the qualitative theory of ordinary differential equations and we refer to [15] for an excellent survey on this subject. In order to motivate our contribution, the crucial reference to be recalled here is the seminal paper [2] by Alonso and Ortega. It is proved therein (cf. [2, Theorem 4.1]) that, for the scalar asymmetric oscillator

$$\begin{aligned} \ddot{x} + a x^+ - b x^- = p(t), \qquad x \in \mathbb {R}, \end{aligned}$$
(1.3)

with \(1/\sqrt{a} + 1/\sqrt{b} = 2/n\), all large solutions are unbounded (either in the past or in the future) whenever the \(2\pi \)-periodic function

$$\begin{aligned} \Phi (\theta ) = \int _0^{2\pi } C\left( \frac{\theta }{n} + t \right) p(t)\,dt, \qquad \theta \in \mathbb {R} \end{aligned}$$
(1.4)

has zeros, all simple (in the above formula, C stands for the asymmetric cosine function, cf. Sect. 2.1). The function \(\Phi \), sometimes referred to as resonance function, was previously introduced by Dancer [7] to investigate the \(2\pi \)-periodic solvability of equation (1.3). In the linear case (\(a= b=n^2\)), the function \(\Phi \) has (simple) zeros if and only if \(\int _0^{2\pi } p(t)e^{-\text {i}nt}\,dt \ne 0\): in this case, as well known, all the solutions of \(\ddot{x} + n^2 x = p(t)\) are unbounded; instead, \(2\pi \)-periodic and unbounded solutions to (1.3) can coexist in the genuinely asymmetric case \(a \ne b\). The proof of this result was obtained by a careful investigation of the dynamics of the associated Poincaré map: more precisely, the zeros of the function \(\Phi \) were shown to give rise to invariant sets for the discrete dynamical system associated with (1.3) and eventually to the existence of unbounded orbits. Generalization of this approach, requiring the introduction of suitable resonance functions, were later provided for forced asymmetric oscillators

$$\begin{aligned} \ddot{x} + a x^+ - b x^- + \phi (x) = p(t), \qquad x \in \mathbb {R}, \end{aligned}$$

with \(\phi : \mathbb {R} \rightarrow \mathbb {R}\) a bounded function (see [6, 9]) and, more in general, for planar system of the type

$$\begin{aligned} Jz' = \nabla H(z) + R(z) + e(t), \qquad z \in \mathbb {R}^2, \end{aligned}$$

where J is the standard symplectic matrix, \(H: \mathbb {R}^2 \rightarrow \mathbb {R}\) is positive and positively homogeneous of degree 2 and \(R: \mathbb {R}^2 \rightarrow \mathbb {R}^2\) is bounded (see [8, 10]). We also refer to [1, 4, 5, 12,13,14, 16, 17] for related results.

In spite of this extensive bibliography, the existence of unbounded solutions for systems of coupled oscillators seems to be an essentially unexplored topic. To the best of our knowledge, the only available results are the ones contained in the recent paper [3], dealing however with systems of equations looking like weakly coupled perturbations of linear oscillators (i.e. \(a_i = b_i = n_i^2\) for \(i=1,2\)) and not being applicable to the more general setting of (1.1).

The aim of the present paper is to extend the approach of [2] in this higher-dimensional framework. As expected, this is a quite delicate task, since it leads to the study of the dynamics of a four-dimensional map; nonetheless, we will succeed in providing some partial generalizations of the results in [2]. In more details, our strategy and results can be described as follows.

In Sect. 2 we pass to an appropriate set of action-angle coordinates and we perform an asymptotic expansion, at infinity, of the Poincaré map associated with (1.1), cf. (2.26). In doing this, we are led to define a resonance function defined on the two-dimensional torus,

$$\begin{aligned} L: \mathbb {T}^2 \rightarrow \mathbb {R}^2, \qquad (\theta _1,\theta _2) \mapsto (L_1(\theta _1,\theta _2),L_2(\theta _1,\theta _2)) \end{aligned}$$

which can be thought as the higher-dimensional generalization of the resonance function \(\Phi \) defined in (1.4), see (2.25)-(2.28). We notice that when system (1.1) is uncoupled (that is, \(\phi _1 = \phi _2 = 0\)), then \(L(\theta _1,\theta _2) = (L_1(\theta _1),L_2(\theta _2))\) and, up to a constant, \(L_i = \Phi \) with \(p = p_i\).

In Sect. 3 we investigate the dynamics of this four-dimensional Poincaré map and we construct invariant sets, giving rise to unbounded orbits. As in the two-dimensional setting, the zeros of the function L are shown to play a role; however, due to the coupling terms in system (1.1), we need here to assume that the Jacobian matrix JL has a special structure at the zeros. More precisely, we introduce the notion of \(\mathcal {D}^{\pm }\)-matrix, cf. Definition 3.1: again, we observe that such a condition is satisfied by diagonal matrices with concordant sign diagonal entries and, hence, by the matrix JL when system (1.1) is uncoupled and the functions \(L_i\) have simple zeros, as in the main result of [2]. This is a quite technical part of the proof, involving, among other things, a delicate estimate for the 2-norm of a two-parameter family of suitable matrices, which are perturbations of the identity by \(\mathcal {D}^{\pm }\)-matrices, cf. Lemma 3.2.

In Sect. 4 we finally give our main result for the existence of unbounded solutions to system (1.1), Theorem 4.1. It provides a positive measure set of initial conditions giving rise to unbounded orbits to (1.1), whenever the function L has a zero \(\omega \in \mathbb {T}^2\) such that the Jacobian matrix \(JL(\omega )\) is a \(\mathcal {D}^{\pm }\)-matrix. Notice that this can be interpreted as a kind of local version of the main result in [2]. Indeed, we do not claim that every large solution of (1.1) is unbounded: due to the higher-dimensional setting, obtaining this global information seems to be a very hard task, even in the case when all the zeros of L are such that the Jacobian at each zero is a \(\mathcal {D}^{\pm }\)-matrix. We mention that the condition for JL to be a \(\mathcal {D}^{\pm }\)-matrix can be, in general, not easy to verify. To this end, we discuss some situations in which this can be done and Theorem 4.1 can thus be applied. The first, quite natural, possibility that we present is a semi-perturbative result (cf. Corollary 4.3), dealing with the case in which the \(L^{\infty }\)-norms of the coupling terms \(\phi _1,\phi _2\) are not too big: it is worth noticing that this provides a genuinely asymmetric (non-quantitative) generalization of a result obtained in [3] for coupled linear oscillators. Other results, more global in nature but focusing on specific choices for the parameters \(a_i, b_i\) or the forcing terms \(p_i\), are given by Corollary 4.6 and Corollary 4.7. It seems that various other situations could be treated at the expenses of longer computations.

We finally mention that it should be possible, with the same approach, to consider also the more general case of resonance with respect to different curves of the Fucik spectrum, that is, \(1/\sqrt{a_i} + 1/\sqrt{b_i} = 2/n_i\) with \(n_i \in \mathbb {N}\). Also, the possibility of coupling more oscillators in a cyclic way \(\phi _{i+1} = \phi _i\) could be considered. All these generalizations, however, seem to require substantial technical modifications of the proofs and they are thus postponed to future investigations.

Notation. Throughout the paper, the symbol \(\Vert \cdot \Vert \) will be used for the Euclidean norm of a vector in the plane. Also, for the index \(i=1,2\), we will adopt the cyclic agreement \(i+1=1\) for \(i=2\).

2 Coupled Asymmetric Oscillators: Some Preliminary Estimates

In this section, we perform some preliminary estimates for the solutions of system (1.1), with the final goal of obtaining an asymptotic expansion for its Poincaré-map in action-angle coordinates (see Sect. 2.2).

From now on, as in the Introduction we will always assume that, for \(i=1,2\), the positive real numbers \(a_i, b_i\) satisfy (1.2), the function \(p_i: \mathbb {R} \rightarrow \mathbb {R}\) is continuous and \(2\pi \)-periodic and the function \(\phi _i: \mathbb {R} \rightarrow \mathbb {R}\) is locally Lipschitz continuous and bounded. Furthermore, we also suppose that there exist

$$\begin{aligned} \lim _{x\rightarrow \pm \infty } \phi _i(x):=\phi _i(\pm \infty ); \end{aligned}$$
(2.1)

moreover, without loss of generality,

$$\begin{aligned} \phi _i(-\infty )=-\phi _i(+\infty ). \end{aligned}$$
(2.2)

2.1 Remarks on the Asymmetric Cosine and Related Functions

We collect here some results on various functions related to the asymmetric cosine function \(C_i\), \(i=1,2\), which is defined as the solution of

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{x}_i+a_ix_i^+-b_ix^-_i=0\\ x_i(0)=1,\ \dot{x}_i(0)=0, \end{array} \right. \end{aligned}$$
(2.3)

with \(a_i\) and \(b_i\) as in (1.2). We recall that, for every \(i=1,2\), the function \(C_i\) is even, \(2\pi /n\)-periodic and its explicit expression in \([-\pi /n,\pi /n]\) is

$$\begin{aligned} C_i(t)=\left\{ \begin{array}{ll} \cos \sqrt{a_i}t&{}{}\text { if } |t|\le \dfrac{\pi }{2\sqrt{a_i}} \\ \displaystyle {-\sqrt{\dfrac{a_i}{b_i}}\sin \sqrt{b_i}\left( |t|-\dfrac{\pi }{2\sqrt{a_i}}\right) }&{}{}\text { if } \dfrac{\pi }{2\sqrt{a_i}}\le |t|\le \dfrac{\pi }{n}. \end{array} \right. \end{aligned}$$
(2.4)

For future reference, let us observe that \(C_i\), \(i=1, 2\), when \(a_i\ne b_i\) admits the Fourier series expansion

$$\begin{aligned} C_i(t)=\sum _{h=0}^{+\infty } c_{h,i} \cos hnt,\quad t\in {\mathbb R}, \end{aligned}$$
(2.5)

where

$$\begin{aligned} c_{0,i} = \dfrac{n}{\pi }\, \dfrac{b_i-a_i}{b_i \sqrt{a_i}} \end{aligned}$$

and, for \(h \ge 1\),

$$\begin{aligned} c_{h,i} = \left\{ \begin{array}{ll} \dfrac{2n}{\pi }\, \dfrac{b_i-a_i}{b_i-h^2 n^2}\, \dfrac{\sqrt{a_i}}{a_i-h^2 n^2}\, \cos \dfrac{hn\pi }{2\sqrt{a_i}} &{} \text {if } a_i \ne h^2 n^2, \,b_i \ne h^2 n^2, \\ \dfrac{1}{2h} &{} \text {otherwise} \end{array} \right. \end{aligned}$$
(2.6)

(see [2, Lemma 4.2]).

In the next sections we will use the integrals of \(C_i\) over the sets \(J^\pm _{i+1}\) defined by

$$\begin{aligned} \displaystyle {J^+_{i+1}=\left\{ t\in [0,2\pi ]:\ C_{i+1}\left( \dfrac{\theta _{i+1}}{n}+t\right) >0\right\} ,\quad J^-_{i+1}=\left\{ t\in [0,2\pi ]:\ C_{i+1}\left( \dfrac{\theta _{i+1}}{n}+t\right) <0\right\} }\nonumber \\ \end{aligned}$$
(2.7)

where \(\theta _{i+1}\in {\mathbb R}\). It is immediate to observe that the fact that \(C_i\) and \(C_{i+1}\) are both \(2\pi /n\)-periodic implies that

$$\begin{aligned} \int _{J^{\pm }_{i+1}} C_{i}\left( \dfrac{\theta _{i}}{n}+t\right) \,dt, \quad \theta _i\in {\mathbb R}, \end{aligned}$$

does not change if we replace \([0,2\pi ]\) in the definition of \(J^{\pm }_{i+1}\) by any interval of lenght \(2\pi \). In particular, in the computation of the integral of \(C_{i}\) on \(J_{i+1}^{+}\), we can replace \(J^+_{i+1}\) by the set

$$\begin{aligned} \bigcup _{k=0}^{n-1} \left( -\dfrac{\pi }{2\sqrt{a_i}}-\dfrac{\theta _{i+1}}{n}+2k\dfrac{\pi }{n}, \dfrac{\pi }{2\sqrt{a_i}}-\dfrac{\theta _{i+1}}{n}+2k\dfrac{\pi }{n}\right) , \end{aligned}$$

thus obtaining that

$$\begin{aligned} \int _{J^+_{i+1}} C_{i}\left( \dfrac{\theta _{i}}{n}+t\right) \,dt= n\Lambda _i (\theta _i-\theta _{i+1}),\quad \forall \ \theta _i,\theta _{i+1}\in {\mathbb R}, \quad i=1,2, \end{aligned}$$
(2.8)

where \(\Lambda _i:{\mathbb R}\rightarrow {\mathbb R}\) is defined by

$$\begin{aligned} \Lambda _i(t)=K_i\left( \dfrac{t}{n}+\dfrac{\pi }{2\sqrt{a_{i+1}}}\right) -K_i\left( \dfrac{t}{n}-\dfrac{\pi }{2\sqrt{a_{i+1}}}\right) ,\quad \forall \ t\in {\mathbb R}, \end{aligned}$$
(2.9)

being \(K_i\) the primitive of \(C_i\) such that \(K_i(0)=0\).

A crucial point in our analysis will be the study of the resolubility of the equation

$$\begin{aligned} \Lambda _i(t)=\alpha _i, \end{aligned}$$
(2.10)

where \(\alpha _i\) is given by

$$\begin{aligned} \alpha _i = \dfrac{1}{\sqrt{a_i}}-\dfrac{\sqrt{a_i}}{b_i},\quad i=1,2, \end{aligned}$$
(2.11)

which is related to \(C_i\) by

$$\begin{aligned} \int _0^{2\pi } C_{i}\left( t\right) \,dt=2n\alpha _i,\quad i=1,2. \end{aligned}$$
(2.12)

In particular, we will be interested in the situation where (2.10) has simple solutions; in order to face this problem, let us first concentrate on the range of the function \(\Lambda _i\). Introducing the function \(\Sigma _i:{\mathbb R}\rightarrow {\mathbb R}\) defined by

$$\begin{aligned} \Sigma _i(t)=n\Lambda '_i(t),\quad \forall \ t\in {\mathbb R}, \end{aligned}$$
(2.13)

is it possible to prove the following result.

Lemma 2.1

The function \(\Lambda _{i}\) given in (2.9) is even, \(2\pi \)-periodic, decreasing in \((0,\pi )\) and increasing in \((-\pi ,0)\).

Proof

Let us first observe that we have

$$\begin{aligned} \Sigma _i(t) = C_i\left( \dfrac{t}{n}+\dfrac{\pi }{2\sqrt{a_{i+1}}}\right) -C_i\left( \dfrac{t}{n}-\dfrac{\pi }{2\sqrt{a_{i+1}}}\right) = C_i^n\left( t+\dfrac{n\pi }{2\sqrt{a_{i+1}}}\right) -C_i^{n}\left( t-\dfrac{n\pi }{2\sqrt{a_{i+1}}}\right) \end{aligned}$$

for all \( t\in {\mathbb R},\) where \(C_i^n:{\mathbb R}\rightarrow {\mathbb R}\) is defined by

$$\begin{aligned} C^n_i(t)=C_i\left( \dfrac{t}{n}\right) ,\quad \forall \ t\in {\mathbb R}. \end{aligned}$$

The function \(C^n_i\) is continuous, \(2\pi \)-periodic, even and strictly decreasing in \([0,\pi )\); as a consequence, \(\Sigma _i\) is continuous, \(2\pi \)-periodic and odd. As far as the sign of \(\Sigma _i\) is concerned, let us observe that \(\Sigma _{i}(t)=0\) if and only if \( t=k\pi \) for some \(k\in {\mathbb Z}\). Indeed, \(\Sigma _{i}(t)=0\) if and only if:

$$\begin{aligned}&\text {either } t + \frac{n\pi }{2\sqrt{a_{i+1}}} = t - \frac{n\pi }{2\sqrt{a_{i+1}}} +2k\pi \quad \text {or}\quad \\&\quad t + \frac{n\pi }{2\sqrt{a_{i+1}}} = -t + \frac{n\pi }{2\sqrt{a_{i+1}}} +2k\pi \quad \text {for some } k\in {\mathbb Z}. \end{aligned}$$

Now, since \(a_{i+1}>n^{2}/4\), the first alternative cannot hold, and the second one implies that \(t=k\pi \). Therefore \(\Sigma _{i}\) has constant sign in \((0,\pi )\) and a straightforward argument shows that

$$\begin{aligned} \Sigma _{i}\left( \pi -\frac{n\pi }{2\sqrt{a_{i+1}}}\right) < 0. \end{aligned}$$

From the above described properties of \(\Sigma _i\) we immediately deduce the thesis. \(\square \)

From now on, in order to simplify the notation, let us continue with the case \(i=1\); the case \(i=2\) is completely analogous.

From Lemma 2.1 we deduce that equation (2.10), with \(i=1\), admits simple solutions if and only if

$$\begin{aligned} \Lambda _1(\pi )< \alpha _1 < \Lambda _1(0); \end{aligned}$$

in general, the validity of this condition depends on the original pairs \((a_1,b_1)\) and \((a_2,b_2)\). Hence, let us define the resolubility set

$$\begin{aligned} \mathcal {R}=\left\{ (a_{1},a_{2})\in \left( \dfrac{n^2}{4},+\infty \right) \times \left( \dfrac{n^2}{4},+\infty \right) \subset \mathbb {R}^2 : \ \Lambda _1(\pi )<\alpha _1<\Lambda _1(0) \right\} . \end{aligned}$$
(2.14)

The complete description of the open set \(\mathcal {R}\) is quite difficult; by means of long computations it is possible to show that the vertical sections \(\mathcal {R}\cap \{(a_1^*,a_2):\ a_2>n^2/4\}\), with \(a_1^*>n^2/4,\ a_1^*\ne n^2\), are bounded. On the other hand, the study of the horizontal sections \(\mathcal {R}\cap \{(a_1,a_2^*):\ a_1>n^2/4\}\), with \(a_2^*>n^2/4,\ a_2^*\ne n^2\), is much more complicated. However, the following simple result holds true.

Lemma 2.2

The set \(\mathcal {R}\) contains the half-lines \( \{(n^{2},a_{2}): a_{2}>n^{2}/4 \} \) and \(\{(a_{1},n^{2}):a_{1}>n^{2}/4\}\).

Proof

Let us first assume that \(a_{1}=n^{2}\) (and, thus, \(b_{1}=n^{2}\)) and fix \(\sqrt{a_{2}} > n/2 \); we then have

$$\begin{aligned} C_{1}(t) = \cos (nt), \quad K_{1}(t) = \frac{1}{n}\sin (nt), \quad \Lambda _{1}(t) = \frac{2}{n} \sin \frac{\pi n}{2\sqrt{a_{2}}} \cos t, \quad \forall t \in {\mathbb R}. \end{aligned}$$

A simple computation proves that \(\Lambda _{1}(\pi )< 0 < \Lambda _{1}(0) \); noticing that \(\alpha _{1}=0\), by (2.11), this shows that \((n^2,a_2)\in \mathcal {R}\).

On the other hand, if \(a_{2}=n^{2}\), we have

$$\begin{aligned} \Lambda _{1}(0) = 2\int _{0}^{\pi /2n} C_{1}(t)dt,\quad \Lambda _{1}(\pi ) = 2\int _{\pi /2n}^{\pi /n} C_{1}(t)dt. \end{aligned}$$

Recalling (2.12), we deduce that \(\Lambda _{1}(\pi ) = 2\alpha _{1} - \Lambda _{1}(0) < \Lambda _{1}(0) \) and, thus, \(\alpha _{1} < \Lambda _{1}(0)\). From these relations we also obtain \(\Lambda _{1}(\pi ) = 2\alpha _{1} - \Lambda _{1}(0)< \alpha _{1}\), proving that \((a_1,n^2)\in \mathcal {R}\). \(\square \)

2.2 Asymptotic Analysis

We now perform an asymptotic expansion of the Poincaré map associated to (1.1). We adapt the argument of the proof of [2, Theorem 4.1] to our case: we write (1.1) as a first order system in \((x_1,x_2,y_1,y_2)=(x_1,x_2,\dot{x}_{1},\dot{x}_{2})\) and use the change of variables

$$\begin{aligned} \left\{ \begin{aligned} x_i&= \gamma _i r_i C_i\left( \dfrac{\theta _{i}}{n}\right) \\ y_i&= \gamma _i r_i S_i\left( \dfrac{\theta _{i}}{n}\right) \end{aligned} \right. \quad \text {with } \gamma _i=\sqrt{2n/a_i}, \end{aligned}$$
(2.15)

where \(S_i(t)=C'_{i}(t)\) and \(C_i\) is defined in Subsection 2.1.

It is straightforward to see that (1.1) is formally equivalent to

$$\begin{aligned} \left\{ \begin{aligned} \dot{\theta }_{1}&= n-\dfrac{\gamma _1}{2r_{1}}C_1\left( \dfrac{\theta _{1}}{n}\right) \left[ p_1(t)-\phi _1\left( \gamma _2r_{2}C_2\left( \dfrac{\theta _{2}}{n}\right) \right) \right] \\ \dot{\theta }_{2}&= n-\dfrac{\gamma _2}{2r_{2}}C_2\left( \dfrac{\theta _{2}}{n}\right) \left[ p_2(t)-\phi _2\left( \gamma _1r_{1}C_1\left( \dfrac{\theta _{1}}{n}\right) \right) \right] \\ \dot{r}_{1}&= \dfrac{\gamma _1}{2n} S_1\left( \dfrac{\theta _{1}}{n}\right) \left[ p_1(t)-\phi _1\left( \gamma _2r_{2}C_2\left( \dfrac{\theta _{2}}{n}\right) \right) \right] \\ \dot{r}_{2}&= \dfrac{\gamma _2}{2n} S_2\left( \dfrac{\theta _{2}}{n}\right) \left[ p_2(t)-\phi _2\left( \gamma _1r_{1}C_1\left( \dfrac{\theta _{1}}{n}\right) \right) \right] \end{aligned} \right. \end{aligned}$$
(2.16)

We denote by \((\theta _1,\theta _2,r_1,r_2)(t)\) the solution of (2.16) satisfying \((\theta _1,\theta _2,r_1,r_2)(0)=(\theta _{1,0},\theta _{2,0},r_{1,0},r_{2,0})\) and study the behavior of \((\theta _1,\theta _2,r_1,r_2)(2\pi )\) as \( \min \{r_{1,0},r_{2,0}\}\rightarrow +\infty \). We also set \( \theta _{0} = (\theta _{1,0},\theta _{2,0}) \), \( r_{0} = (r_{1,0},r_{2,0}) \) and remark that \( \theta _{0} \in {\mathbb R}^{2} \) and \( r_{1,0}, r_{2,0} > 0 \).

The boundedness of \(p_i\) and \(\phi _i\) implies that \(\dot{r}_{i}\) is uniformly bounded and, hence, we have

$$\begin{aligned} r_{i}=r_{i,0}+O(1) \qquad \text {and}\qquad r_{i}^{-1} = r_{i,0}^{-1}+O(r_{i,0}^{-2}) \qquad \text {as } r_{i,0}\rightarrow +\infty , \end{aligned}$$
(2.17)

where these and all the following estimates hold uniformly w.r.t. \(t\in [0,2\pi ]\), \(\theta _{1,0}\), \(\theta _{2,0}\) and \(r_{i+1,0}\). We deduce that

$$\begin{aligned} \begin{aligned} \dot{\theta }_i&= n-\dfrac{\gamma _i}{2} C_i\left( \dfrac{\theta _{i}}{n}\right) \left( \dfrac{1}{r_{i,0}}+O(r_{i,0}^{-2})\right) \left[ p_i(t)- \phi _i\left( \gamma _{i+1} r_{i+1}C_{i+1}\left( \dfrac{\theta _{i+1}}{n}\right) \right) \right] \\&= n-\dfrac{\gamma _i}{2 r_{i,0}} C_i\left( \dfrac{\theta _{i}}{n}\right) \left[ p_i(t)- \phi _i\left( \gamma _{i+1} r_{i+1}C_{i+1}\left( \dfrac{\theta _{i+1}}{n}\right) \right) \right] +O(r_{i,0}^{-2}), \end{aligned} \qquad \text {as } r_{i,0}\rightarrow +\infty . \end{aligned}$$
(2.18)

This relation implies that

$$\begin{aligned} \dfrac{\theta _{i}}{n}=\dfrac{\theta _{i,0}}{n}+t+O(r_{i,0}^{-1}),\qquad \text {as } r_{i,0}\rightarrow +\infty ; \end{aligned}$$

and, thus:

$$\begin{aligned} \begin{aligned} C_i\left( \dfrac{\theta _{i}}{n}\right)&= C_i\left( \dfrac{\theta _{i,0}}{n}+t\right) +O(r_{i,0}^{-1}) \\ S_i\left( \dfrac{\theta _{i}}{n}\right)&= S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) +O(r_{i,0}^{-1}) \end{aligned} \qquad \text {as } r_{i,0}\rightarrow +\infty , \end{aligned}$$
(2.19)

since \(C_{i}\) and \(S_{i}\) are smooth enough. By replacing (2.19) in the last two equations of (2.16) we get

$$\begin{aligned} \dot{r}_{i} = \dfrac{\gamma _i}{2n} S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) \left[ p_i(t)- \phi _i\left( \gamma _{i+1}r_{i+1}C_{i+1}\left( \frac{\theta _{i+1}}{n}\right) \right) \right] +O(r_{i,0}^{-1}) \qquad \text {as } r_{i,0}\rightarrow +\infty . \end{aligned}$$

As a consequence, we infer that

$$\begin{aligned} \begin{aligned} r_i(2\pi )&= r_{i,0} +\dfrac{\gamma _i}{2n}\int _0^{2\pi } S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) p_i(t) \,dt \\&\quad -\dfrac{\gamma _i}{2n} \int _0^{2\pi } S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) \phi _i\left( \gamma _{i+1}r_{i+1}C_{i+1}\left( \frac{\theta _{i+1}}{n}\right) \right) dt +F_{i,i}(\theta _0,r_0) \end{aligned} \end{aligned}$$
(2.20)

where

$$\begin{aligned} \lim _{r_{i,0}\rightarrow +\infty } F_{i,i}(\theta _0,r_0) = 0 \quad \text {uniformly w.r.t. } \theta _{1}, \theta _{2}, \text { and } r_{i+1,0}. \end{aligned}$$

Now, we deduce from (2.19) that \( C_{i+1}(\theta _{i+1}(t)/n) \rightarrow C_{i+1}(\theta _{i+1,0}/n+t) \) uniformly w.r.t. \( t\in [0,2\pi ]\), \(\theta _{1,0}\), \(\theta _{2,0}\) and \(r_{i,0}\), as \( r_{i+1,0} \rightarrow +\infty \) and, setting

$$\begin{aligned} \begin{aligned}&J^{+}_{i+1,0}=\left\{ t\in [0,2\pi ]:\ C_{i+1}\left( \frac{\theta _{i+1,0}}{n}+t\right) >0\right\} \\&J^{-}_{i+1,0}=\left\{ t\in [0,2\pi ]:\ C_{i+1}\left( \frac{\theta _{i+1,0}}{n}+t\right) <0\right\} , \end{aligned} \end{aligned}$$

we have that

$$\begin{aligned} t\in J^{\pm }_{i+1,0} \implies \lim _{r_{i+1,0}\rightarrow +\infty } \phi _i\left( \gamma _{i+1}r_{i+1}C_{i+1}\left( \frac{\theta _{i+1}}{n}\right) \right) = \phi _{i}(\pm \infty ), \end{aligned}$$

where these two limits are not uniform w.r.t. \(t\in [0,2\pi ]\). However, using that \( \phi _{i} \) is bounded and \( C_{i+1}(\theta _{i+1}(t)/n) \) converges uniformly, it is possible to show that:

$$\begin{aligned} \lim _{r_{i+1,0}\rightarrow +\infty }\int _{J^{\pm }_{i+1,0}} S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) \left[ \phi _{i}(\pm \infty ) - \phi _i\left( \gamma _{i+1}r_{i+1}C_{i+1}\left( \frac{\theta _{i+1}}{n}\right) \right) \right] dt =0 \end{aligned}$$

uniformly w.r.t. \(\theta _{1,0}\), \(\theta _{2,0}\) and \(r_{i,0}\). Therefore, we can write equation (2.20) in the following way:

$$\begin{aligned} \begin{aligned} r_i(2\pi )&= r_{i,0} +\dfrac{\gamma _i}{2n}\int _0^{2\pi } S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) p_i(t) \,dt \\&\quad -\dfrac{\gamma _i}{2n} \left( \phi _i(+\infty ) \int _{J^+_{i+1,0}} S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) \,dt +\phi _i(-\infty ) \int _{J^-_{i+1,0}} S_i\left( \dfrac{\theta _{i,0}}{n}+t\right) \,dt\right) \\&\quad +F_{i,i}(\theta _0,r_0)+F_{i,i+1}(\theta _0,r_0), \end{aligned} \end{aligned}$$
(2.21)

where also

$$\begin{aligned} \lim _{r_{i+1,0}\rightarrow +\infty } F_{i,i+1}(\theta _0,r_0)=0 \qquad \text {uniformly w.r.t. } \theta _{1,0}, \theta _{2,0} \text { and } r_{i,0}. \end{aligned}$$
(2.22)

We now substitute (2.17) and (2.19) in (2.18), obtaining

$$\begin{aligned} \dot{\theta }_i = n-\dfrac{\gamma _i}{2r_{i,0}} C_i\left( \dfrac{\theta _{i,0}}{n} + t \right) \left[ p_i(t)- \phi _i\left( \gamma _{i+1} r_{i+1}C_{i+1}\left( \dfrac{\theta _{i+1}}{n}\right) \right) \right] + O(r_{i,0}^{-2}), \qquad \text {as } r_{i,0}\rightarrow +\infty . \end{aligned}$$

Integrating on \([0,2\pi ]\) and making similar considerations as done for \( r_{i}(2\pi ) \), we deduce that

$$\begin{aligned} \begin{aligned} \theta _i(2\pi )&= \theta _{i,0}+2n\pi - \dfrac{\gamma _i}{2r_{i,0}} \int _0^{2\pi } C_i\left( \dfrac{\theta _{i,0}}{n} + t \right) p_i(t)\,dt \\&\quad + \dfrac{\gamma _i}{2r_{i,0}} \left( \phi _i(+\infty ) \int _{J^+_{i+1,0}} C_i\left( \dfrac{\theta _{i,0}}{n} + t \right) \,dt +\phi _i(-\infty ) \int _{J^-_{i+1,0}} C_i\left( \dfrac{\theta _{i,0}}{n} + t \right) \,dt\right) \\&\quad +\dfrac{1}{r_{i,0}} \left( G_{i,i}(\theta _0,r_0)+G_{i,i+1}(\theta _0,r_0)\right) , \end{aligned} \end{aligned}$$
(2.23)

where

$$\begin{aligned} \lim _{r_{i,0}\rightarrow +\infty } G_{i,i}(\theta _0,r_0) =\lim _{r_{i+1,0}\rightarrow +\infty } G_{i,i+1}(\theta _0,r_0)=0 \end{aligned}$$
(2.24)

uniformly w.r.t. the other variables.

Recalling (2.2), we observe that (2.8) and (2.12) imply that \(\theta _{i}(2\pi )\), \(i=1,2\), can be written as

$$\begin{aligned} \begin{aligned} \theta _i(2\pi )&= \theta _{i,0}+2n\pi - \dfrac{\gamma _i}{2r_{i,0}} \int _0^{2\pi } C_i\left( \dfrac{\theta _{i,0}}{n} + t \right) p_i(t)\,dt\\&\quad + \frac{1}{r_{i,0}} \gamma _{i}n\phi _{i}(+\infty )(\Lambda _{i}(\theta _{i,0}-\theta _{i+1,0})-\alpha _{i}) +\dfrac{1}{r_{i,0}} \left( G_{i,i}(\theta _0,r_0)+G_{i,i+1}(\theta _0,r_0)\right) , \end{aligned} \end{aligned}$$

where \(\alpha _i, \Lambda _i\) are defined in (2.11), (2.9).

For \(i=1, 2\), let us now denote

$$\begin{aligned} \begin{aligned} \Phi _i(\theta _{i,0})&= -\dfrac{\gamma _i}{2}\int _0^{2\pi } C_i\left( \dfrac{\theta _{i,0}}{n}+t\right) p_i(t)\,dt, \\ L_i(\theta _{0})&=\Phi _i(\theta _{i,0}) +\gamma _{i}n\phi _{i}(+\infty )(\Lambda _{i}(\theta _{i,0}-\theta _{i+1,0})-\alpha _{i}), \end{aligned} \end{aligned}$$
(2.25)

for every \(\theta _0 =(\theta _{1,0},\theta _{2,0} )\in {\mathbb R}^{2} \). Then, we can summarize (2.21), (2.22), (2.23) and (2.24) as follows:

$$\begin{aligned} \left\{ \begin{aligned} {\theta _i}(2\pi )&= \theta _{i,0}+2\pi n+\dfrac{1}{r_{i,0}} \left[ L_i(\theta _0)+G_{i,i}(\theta _0,r_0)+G_{i,i+1}(\theta _0,r_0)\right] \\ r_i(2\pi )&= r_{i,0} -\dfrac{\partial L_i}{\partial \theta _{i,0}} (\theta _{0})+F_{i,i}(\theta _0,r_0)+F_{i,i+1}(\theta _0,r_0) \end{aligned} \right. \qquad \text {for } i=1,2, \end{aligned}$$
(2.26)

where

$$\begin{aligned} \begin{aligned}&\lim _{r_{i,0}\rightarrow +\infty } F_{i,i}(\theta _0,r_0) = \lim _{r_{i,0}\rightarrow +\infty } G_{i,i}(\theta _0,r_0) = 0&\text{ uniformly } \text{ w.r.t. } r_{i+1,0} \text{ and } \theta _{0}, \\ {}&\lim _{r_{i+1,0}\rightarrow +\infty } F_{i,i+1}(\theta _0,r_0) =\lim _{r_{i+1,0}\rightarrow +\infty } G_{i,i+1}(\theta _0,r_0)=0&\text{ uniformly } \text{ w.r.t. } r_{i,0} \text{ and } \theta _{0}. \end{aligned} \end{aligned}$$
(2.27)

The functions \(L_1, L_2\) will be meant as the components of the vector valued function

$$\begin{aligned} L(\theta _0) = (L_1(\theta _{0}),L_2(\theta _{0})), \qquad \theta _0 =(\theta _{1,0},\theta _{2,0} )\in {\mathbb R}^{2}. \end{aligned}$$
(2.28)

which we will call resonance function for system (1.1). Notice that, due to the \(2\pi \)-periodicity in both the variables, we can interpret L as a function defined on the two-dimensional torus \(\mathbb {T}^{2} = {\mathbb R}^{2} / (2\pi \mathbb {Z})^{2}\). This function will play a crucial role in the statement of our main result (see Sect. 4).

3 Dynamics of Discrete Maps

In this section, we establish the abstract result that will be used to prove the existence of unbounded solutions to system (1.1).

3.1 \(\mathcal {D}^\pm \)-Matrices

We consider \(2\times 2\)-matrices \(A=(a_{ij})\), \(i,j=1, 2\).

Definition 3.1

A \(2\times 2\)-matrix A is said to be a \(\mathcal {D}^+\)-matrix if

$$\begin{aligned} a_{11}<0,\qquad a_{22}<0, \qquad |a_{12}a_{22}+a_{11}a_{21}|<2a_{11}a_{22}. \end{aligned}$$
(3.1)

Analogously, a \(2\times 2\)-matrix A is said to be a \(\mathcal {D}^-\)-matrix if

$$\begin{aligned} a_{11}>0,\qquad a_{22}>0, \qquad |a_{12}a_{22}+a_{11}a_{21}|<2a_{11}a_{22}. \end{aligned}$$
(3.2)

Notice that a diagonal matrix with negative entries (resp., positive entries) is a \(\mathcal {D}^+\) matrix (resp., \(\mathcal {D}^-\) matrix). Given a \(\mathcal {D}^\pm \)-matrix A and \(\epsilon =(\epsilon _1,\epsilon _2)\in (0,+\infty )^2\), let us define

$$\begin{aligned} B_{\epsilon } =\begin{pmatrix} 1+\epsilon _1 a_{11}&{}\epsilon _1 a_{12}\\ &{}\\ \epsilon _2 a_{21}&{}1+\epsilon _2 a_{22} \end{pmatrix}. \end{aligned}$$
(3.3)

Moreover, for every \(\epsilon _0>0\) and \(\eta >0\) let us define

$$\begin{aligned} C_{\epsilon _0,\eta }=\left\{ \epsilon =(\epsilon _1,\epsilon _2)\in (0,+\infty )^2:\ \dfrac{a_{11}}{a_{22}}-\eta \le \dfrac{\epsilon _2}{\epsilon _1}\le \dfrac{a_{11}}{a_{22}}+\eta ,\quad \Vert \epsilon \Vert \le \epsilon _0\right\} . \end{aligned}$$
(3.4)

We prove the following result.

Lemma 3.2

Assume that A is a \(\mathcal {D}^\pm \)-matrix. Then, there exist \(a_0>0\), \(\epsilon _0>0\) and \(\eta >0\) such that

$$\begin{aligned} \Vert B_{\epsilon }\Vert _{2} \le 1-\dfrac{1}{2}a_0\Vert \epsilon \Vert ,\quad \forall \ \epsilon \in C_{\epsilon _0,\eta }. \end{aligned}$$
(3.5)

Proof

We give the proof in the case of \(\mathcal {D}^+\)-matrix; the other case is analogous. We recall that the matrix norm \(\Vert B_{\epsilon }\Vert _{2}\) coincides with the square root of the maximum eigenvalue of the matrix \(C_\epsilon =B_\epsilon ^T\, B_\epsilon \).

Let us first observe that, for every \(\epsilon \), the elements on the diagonal of \(C_\epsilon \) are given by

$$\begin{aligned} (1+\epsilon _1 a_{11})^2+\epsilon _2^2 a_{21}^2,\quad (1+\epsilon _2 a_{22})^2+\epsilon _1^2 a_{12}^2; \end{aligned}$$

hence, we have

$$\begin{aligned} \mathrm{tr} (C_\epsilon )=2+2(a_{11}\epsilon _1+a_{22}\epsilon _2)+(a_{11}^2+a_{12}^2)\epsilon _1^2+(a_{22}^2+a_{21}^2)\epsilon _2^2. \end{aligned}$$
(3.6)

Hence, a simple computation shows that

$$\begin{aligned} \left( \mathrm{tr} (C_\epsilon )\right) ^2= & {} 4+8(a_{11}\epsilon _1+a_{22}\epsilon _2)+4(a_{11}\epsilon _1+a_{22}\epsilon _2)^2+4(a_{11}^2+a_{12}^2)\epsilon _1^2+4(a_{22}^2+a_{21}^2)\epsilon _2^2+\nonumber \\&+4(a_{11}\epsilon _1+a_{22}\epsilon _2)((a_{11}^2+a_{12}^2)\epsilon _1^2+(a_{22}^2+a_{21}^2)\epsilon _2^2)+((a_{11}^2+a_{12}^2)\epsilon _1^2+(a_{22}^2+a_{21}^2)\epsilon _2^2)^2.\nonumber \\ \end{aligned}$$
(3.7)

On the other hand, we have

$$\begin{aligned} \begin{array}{ll} {\det } (C_\epsilon )=(\det B_\epsilon )^2=&{} 1+ 2(a_{11}\epsilon _1+a_{22}\epsilon _2)+(a_{11}\epsilon _1+a_{22}\epsilon _2)^2+2\Delta \epsilon _1 \epsilon _2+\\ &{}\\ &{}+2(a_{11}\epsilon _1+a_{22}\epsilon _2)\Delta \epsilon _1 \epsilon _2+\Delta ^2 \epsilon _1^2 \epsilon _2^2, \end{array} \end{aligned}$$
(3.8)

where \(\Delta =a_{11}a_{22}-a_{12}a_{21}\).

Now, let us observe that the matrix \(C_\epsilon \) is positive definite; as a consequence, the maximum eigenvalue of \(C_\epsilon \) is given by

$$\begin{aligned} \lambda _+(\epsilon )=\dfrac{\mathrm{tr}(C_\epsilon )+\sqrt{(\mathrm{tr}(C_\epsilon ))^2-4\det (C_\epsilon )}}{2}. \end{aligned}$$
(3.9)

From (3.7) and (3.8), by means of simple computations we infer that

$$\begin{aligned} \sqrt{(\mathrm{tr}(C_\epsilon ))^2-4\det (C_\epsilon )} =2 \sqrt{ (1+a_{11}\epsilon _1 +a_{22}\epsilon _2)d_2(\epsilon ) +P_4(\epsilon )}, \end{aligned}$$
(3.10)

where

$$\begin{aligned} d_2(\epsilon )=(a_{11}^2+a_{12}^2)\epsilon _1^2-2\Delta \epsilon _1 \epsilon _2+(a_{21}^2+a_{22}^2)\epsilon _2^2 = (a_{11}\epsilon _{1}-a_{22}\epsilon _{2})^{2}+(a_{12}\epsilon _{1}+a_{21}\epsilon _{2})^{2}\nonumber \\ \end{aligned}$$
(3.11)

and

$$\begin{aligned} \begin{aligned} P_4(\epsilon )&= \dfrac{1}{4}\left[ (a_{11}^2+a_{12}^2)\epsilon _1^2+(a_{22}^2+a_{21}^2)\epsilon _2^2\right] ^2 -\Delta ^2 \epsilon _1^2 \epsilon _2^2 \\ {}&= \dfrac{1}{4} d_{2}(\epsilon )\left[ (a_{11}^2+a_{12}^2)\epsilon _1^2+(a_{22}^2+a_{21}^2)\epsilon _2^2 +2\Delta \epsilon _1 \epsilon _2\right] \\ {}&= d_{2}(\epsilon ) \cdot O(\Vert \epsilon \Vert ^{2}) \qquad \text{ as } \epsilon \rightarrow 0. \end{aligned} \end{aligned}$$
(3.12)

Using (3.6) and (3.9)–(3.12), we can estimate:

$$\begin{aligned} \begin{aligned} \lambda _+(\epsilon )&= 1 + a_{11}\epsilon _1+a_{22}\epsilon _2+O(\Vert \epsilon \Vert ^{2}) + \sqrt{d_2(\epsilon )} \, \sqrt{1+a_{11}\epsilon _1 +a_{22}\epsilon _2 +O(\Vert \epsilon \Vert ^{2})} \\&= 1+ g(\epsilon ) + O(\Vert \epsilon \Vert ^{2}) \qquad \text {as } \epsilon \rightarrow 0, \end{aligned} \end{aligned}$$
(3.13)

where:

$$\begin{aligned} g(\epsilon )=a_{11}\epsilon _1+a_{22}\epsilon _2+\sqrt{d_2(\epsilon )}. \end{aligned}$$

Observe that g is a positively homogeneous function of degree 1. A simple computation shows that

$$\begin{aligned} g\left( -\dfrac{a_{22}}{\sqrt{a_{11}^2+a_{22}^2}},-\dfrac{a_{11}}{\sqrt{a_{11}^2+a_{22}^2}}\right) =\dfrac{-2a_{11}a_{22}+|a_{12}a_{22}+a_{11}a_{21}|}{a_{11}^2+a_{22}^2}:=-4a_0<0, \end{aligned}$$
(3.14)

since the matrix A is a \(\mathcal {D}^+\)-matrix. Using (3.14) we deduce that there exists \(\eta >0\) such that

$$\begin{aligned} g\left( \epsilon \right) <-2a_0, \end{aligned}$$
(3.15)

for every \(\epsilon \) such that \(\Vert \epsilon \Vert =1\) and

$$\begin{aligned} 0<\dfrac{a_{11}}{a_{22}}-\eta \le \dfrac{\epsilon _2}{\epsilon _1}\le \dfrac{a_{11}}{a_{22}}+\eta . \end{aligned}$$
(3.16)

By homogeneity, we conclude that

$$\begin{aligned} g\left( \epsilon \right) <-2a_0\Vert \epsilon \Vert , \end{aligned}$$
(3.17)

for every \(\epsilon \in (0,+\infty )^2\) satisfying (3.16).

From (3.13) and (3.17) we deduce that there exists \(\bar{\epsilon }>0\) such that

$$\begin{aligned} \lambda _+(\epsilon )\le 1-a_0\Vert \epsilon \Vert , \end{aligned}$$
(3.18)

for every \(\epsilon \in C_{{\bar{\epsilon }},\eta }\). Let us now take \(\epsilon _0=\min \{{\bar{\epsilon }},1/a_0\}\); from (3.18) we immediately conclude that

$$\begin{aligned} \sqrt{\lambda _+(\epsilon )}\le 1-\dfrac{1}{2}\, a_0 \Vert \epsilon \Vert , \end{aligned}$$

for every \(\epsilon \in C_{{\epsilon }_0,\eta }\). \(\square \)

3.2 Invariant Sets and Unbounded Orbits of Discrete Maps

In (2.26) we have obtained an estimate for the Poincaré map \( (\theta (0), r(0)) \mapsto (\theta (2\pi ), r(2\pi )) \) associated to the system (2.16) when both components \(r_{1,0}\) and \(r_{2,0}\) of r(0) are large. Here we provide sufficient conditions under which the discrete dynamical systems generated by similar maps possess invariant sets that contain unbounded trajectories.

Few words are in order to clarify the setting in which the dynamical system is defined and represented. Equations (2.26) define a map \( (\theta ,r) \mapsto (u,\rho ) \), with \( \theta = ( \theta _{1}, \theta _{2} ) \), \(r = ( r_{1}, r_{2} ) \), \( u = ( u_{1}, u_{2} ) \) and \( \rho = ( \rho _{1}, \rho _{2} ) \), such that:

$$\begin{aligned} \left\{ \begin{aligned} u&= \theta + \left[ \begin{array}{c} 2\pi n_1 \\ 2\pi n_2\end{array} \right] + \left[ \begin{array}{c} L_1(\theta )/r_{1} \\ L_2(\theta )/r_{2} \end{array} \right] + \left[ \begin{array}{c} G_1(\theta ,r)/r_{1} \\ G_2(\theta ,r)/r_{2} \end{array} \right] \\ \rho&= r - \left[ \begin{array}{c} \partial _{1}L_1(\theta ) \\ \partial _{2}L_2(\theta )\end{array}\right] + F(\theta ,r), \end{aligned} \right. \end{aligned}$$
(3.19)

where \( n_{1},n_{2}\in \mathbb {N} \), \( G(\theta ,r)=(G_{1}(\theta ,r),G_{2}(\theta ,r))\) and \( F(\theta ,r)=(F_{1}(\theta ,r),F_{2}(\theta ,r))\) are continuous, \( L(\theta )=(L_{1}(\theta ),L_{2}(\theta ))\) is a \(C^{1}\)-function with \( \partial _{j}L_{i} = \partial L_{i}/\partial \theta _{j} \), and, moreover, L, G, F are all \(2\pi \)-periodic w.r.t. \(\theta _{1}\) and \(\theta _{2}\). We recall that \( ( \theta _{i}, r_{i} ) \) and \( ( u_{i}, \rho _{i} ) \) are modified polar coordinates in \( {\mathbb R}^{2} \) according to (2.15) and, hence, there is a couple of well known issues to take into account.

The first one concerns the singularity of polar coordinates whenever the radius vanishes and will be easily dealt with since the invariant sets we are going to define will be contained in a region where \( \min \{ r_{1}, r_{2}\} \ge R > 0 \).

The second issue is that (3.19) defines a lifting of the actual dynamical system that, indeed, acts on \( \mathbb {T}^{2} \times {\mathbb R}_{+}^{2} \), where, as usual, \( \mathbb {T}^{2} = {\mathbb R}^{2} / (2\pi \mathbb {Z})^{2} \) denotes the two-dimensional torus. More precisely, the coordinates \((\theta ,r)\) and \((u,\rho )\) should be projected to \(\mathbb {T}^{2}\times {\mathbb R}_{+}^{2}\) to determine the correct behavior of the dynamical system, but computations are more easily performed on the “flat” covering space \({\mathbb R}^{2}\times {\mathbb R}_{+}^{2}\). To this aim, we denote by \(\bar{\theta }_{i}\) the equivalence class of \(\theta _{i}\) in \( \mathbb {T}^{1} = {\mathbb R}/2\pi \mathbb {Z} \) and, thus, we will have \(\bar{\theta } = (\bar{\theta }_{1}, \bar{\theta }_{2}) \in \mathbb {T}^{2}\) for each \(\theta =(\theta _{1},\theta _{2})\in {\mathbb R}^{2}\); the group metrics in \(\mathbb {T}^1\) and \(\mathbb {T}^{2} \) are respectively defined by

$$\begin{aligned} |\bar{\theta }_{i} - \bar{u}_{i} |=\min \{|\theta _{i}-u_{i} + 2n\pi |: n\in \mathbb {Z}\} \quad \text {and} \quad \Vert \bar{\theta }- \bar{u}\Vert = \sqrt{ |\bar{\theta }_{1}-\bar{u}_{1}|^{2}+|\bar{\theta }_{2}-\bar{u}_{2}|^{2} }. \end{aligned}$$
(3.20)

It will be clear from the context when \( |\cdot | \) and \( \Vert \cdot \Vert \) are meant on either \( {\mathbb R}\) and \( {\mathbb R}^{2} \) or \(\mathbb {T}^{1}\) and \(\mathbb {T}^{2}\), respectively. In particular, we observe that \( |\bar{\theta }_{i}-\bar{u}_{i}| = |\theta _{i} - u_{i}| \) if and only if \(|\theta _{i} - u_{i}| \le \pi \).

The invariant sets we obtain are built around a fixed \( \bar{\omega }\in \mathbb {T}^{2} \) and depend of four other parameters as follows:

$$\begin{aligned} E_{R,\Theta ,\lambda ,\eta }=\left\{ (\bar{\theta },r)\in \mathbb {T}^{2}\times {\mathbb R}_{+}^{2} : r_1\ge R,\ r_2\ge R,\ \lambda -\eta \le \dfrac{r_1}{r_2}\le \lambda +\eta ,\ \Vert \bar{\theta }-\bar{\omega }\Vert \le \Theta \right\} , \end{aligned}$$
(3.21)

where \(R>0\), \(0<\Theta < \pi \), \(\lambda >0\) and \( 0< \eta < \lambda \). We will denote by \( f :E_{R,\Theta ,\lambda ,\eta }\rightarrow \mathbb {T}^{2}\times {\mathbb R}_{+}^{2}\) the map which has (3.19) as a lifting. We remark that all different choices of \(n_{1},n_{2}\in \mathbb {Z}\) in (3.19) define good liftings of the map f: we will use the choice \(n_{1}=n_{2}=0\) in the proof of the next result.

Theorem 3.3

In the above setting, let us assume that there exists \(\omega \in {\mathbb R}^{2}\) such that \( L(\omega ) = 0 \) and suppose that the Jacobian \(JL(\omega )\) is a \(\mathcal {D}^+\)-matrix. Moreover, assume that

$$\begin{aligned} \lim _{\begin{array}{c} r_i\rightarrow +\infty \\ i=1,2 \end{array}} G(\theta ,r)=0\quad \text {and}\quad \lim _{\begin{array}{c} r_i\rightarrow +\infty \\ i=1,2 \end{array}} F(\theta ,r)=0 \qquad \text {uniformly w.r.t. } \theta . \end{aligned}$$
(3.22)

Then, there exist \(R>0\), \(\Theta \in \left]0,\pi \right[\), \(\lambda >0\) and \(\eta \in \left]0,\lambda \right[\) such that:

$$\begin{aligned} f(E_{R,\Theta ,\lambda ,\eta })\subset E_{R,\Theta ,\lambda ,\eta }. \end{aligned}$$
(3.23)

Proof

We divide the proof into three parts.

Part 1. Choice of the constants \(R, \Theta , \lambda \) and \(\eta \). Let

$$\begin{aligned} \lambda = \dfrac{\partial _1 L_1(\omega )}{\partial _2 L_2(\omega )} > 0, \end{aligned}$$
(3.24)

let \(\eta ,\epsilon _{0} > 0 \) be as in Lemma 3.2 and let \(R_0=1/\epsilon _0\). Since \(JL(\omega )\) is a \(\mathcal {D}^+\)-matrix we deduce that there exist \(\Theta _0\in \left]0,\pi \right[\) and \(\gamma _i>0\), \(i=1, 2\), such that

$$\begin{aligned} \partial _i L_i (\theta )\le -\gamma _i<0,\quad \text {for } i=1,2 \text { and } \forall \theta \in {{\mathbb R}}^2: \Vert \bar{\theta }-\bar{\omega }\Vert \le \Theta _0. \end{aligned}$$
(3.25)

Moreover, according to assumption (3.22), let \(R_1\ge R_0\) such that

$$\begin{aligned} F_i(\theta ,r)\ge -\dfrac{\gamma _i}{2},\quad \text {for } i=1,2 \text { and } \forall \ \theta \in {{\mathbb R}}^2,\ r_1\ge R_1,\ r_2\ge R_1. \end{aligned}$$
(3.26)

By the continuity of \(JL(\theta )\) in \(\theta =\omega \), a simple computation shows that there exists \(\Theta _1\in ]0, \Theta _0]\) such that

$$\begin{aligned} \begin{aligned} \dfrac{\partial _1 L_1(\theta )}{\lambda +\eta }-\partial _2 L_2(\theta )&\ge \dfrac{-\partial _2 L_2(\omega ) \eta }{2(\lambda +\eta )} \\ \partial _2 L_2(\theta )-\dfrac{\partial _1 L_1(\theta )}{\lambda -\eta }&\ge \dfrac{-\partial _2 L_2(\omega ) \eta }{2(\lambda -\eta )} \end{aligned} \qquad \forall \theta :\Vert \bar{\theta }-\bar{\omega }\Vert \le \Theta _1. \end{aligned}$$
(3.27)

Moreover, using again assumption (3.22), we deduce that there exists \(R_2\ge R_1\) such that

$$\begin{aligned} \begin{aligned} \left| F_2(\theta ,r)-\dfrac{F_1(\theta ,r)}{\lambda +\eta }\right|&< \dfrac{-\partial _2 L_2(\omega ) \eta }{2(\lambda +\eta )}\\ \displaystyle \left| \dfrac{F_1(\theta ,r)}{\lambda -\eta }-F_2(\theta ,r)\right|&< \dfrac{-\partial _2 L_2(\omega ) \eta }{2(\lambda -\eta )} \end{aligned} \qquad \text {for each } r_1\ge R_2,\ r_2\ge R_2 \text { and } \theta \in {\mathbb R}^{2}.\nonumber \\ \end{aligned}$$
(3.28)

Now, let us write

$$\begin{aligned} L_{i}(\theta )=\langle \nabla L_i(\omega ),\theta -\omega \rangle +\alpha _i(\theta )\Vert \theta -\omega \Vert , \end{aligned}$$
(3.29)

for \(i=1 ,2\) and \(\theta \in {{\mathbb R}}^2\), with

$$\begin{aligned} \lim _{\theta \rightarrow \omega } \alpha (\theta )=0,\quad i=1,2 \end{aligned}$$

with \(\alpha (\theta ):=(\alpha _{1}(\theta ),\alpha _{2}(\theta ))\). Then, we choose \(\Theta \in ]0,\Theta _1]\) such that

$$\begin{aligned} \Vert (\alpha _1 (\theta ),\alpha _2(\theta ))\Vert \le \dfrac{a_0}{4},\qquad \text {if } \Vert \theta -\omega \Vert \le \Theta , \end{aligned}$$
(3.30)

where \(a_0\) is given in Lemma 3.2.

Let us now define

$$\begin{aligned} L^*=\max \{ \Vert L(\theta )\Vert : \Vert \theta -\omega \Vert \le \Theta /2\}; \end{aligned}$$
(3.31)

according to assumption (3.22), let \(R_3\ge R_2\) be such that

$$\begin{aligned} \displaystyle \Vert G(\theta ,r)\Vert <\min \left\{ L^*, \dfrac{a_0\, \Theta }{8}\, \right\} \quad \text {for every } \theta \in {{\mathbb R}}^2\text { and } r_1, r_2\ge R_3. \end{aligned}$$
(3.32)

Finally, let us fix

$$\begin{aligned} R\ge \max \left\{ R_3, \dfrac{4L^*}{\Theta }\right\} \end{aligned}$$
(3.33)

and consider the set \(E_{R,\Theta ,\lambda ,\eta }\) corresponding to the chosen constants. From now on, we will simply denote this set by E.

Part 2. Invariance of E with respect to the radial components. Let us fix \((\theta ,r)\) such that \((\bar{\theta },r)\in E\) and consider \(\rho =(\rho _{1},\rho _{2}) \) given by (3.19). From conditions (3.25) and (3.26) we immediately deduce that

$$\begin{aligned} \rho _i \ge r_i+\dfrac{\gamma _i}{2} >r_i,\quad \text {for }i=1, 2. \end{aligned}$$
(3.34)

On the other hand, we have \( r_1\le \left( \lambda +\eta \right) r_2 \) and, then, we infer that

$$\begin{aligned} \begin{aligned} \dfrac{\rho _1}{\rho _2}&= \dfrac{r_1-\partial _1 L_1(\theta )+F_1(\theta ,r)}{r_2-\partial _2 L_2(\theta )+F_2(\theta ,r)} \\&\le (\lambda +\eta ) \dfrac{r_2-\dfrac{\partial _1 L_1(\theta )}{\lambda +\eta }+\dfrac{F_1(\theta ,r)}{\lambda +\eta }}{r_2-\partial _2 L_2(\theta )+F_2(\theta ,r)} \\&= (\lambda +\eta ) \left( 1-\dfrac{\dfrac{\partial _1 L_1(\theta )}{\lambda +\eta }-\partial _2 L_2(\theta )+F_2(\theta ,R)-\dfrac{F_1(\theta ,r)}{\lambda +\eta }}{r_2-\partial _2 L_2(\theta )+F_2(\theta ,r)}\right) . \end{aligned} \end{aligned}$$
(3.35)

Let us now observe that (3.34) implies that \(r_2-\partial _2 L_2(\theta )+F_2(\theta ,r)>0\) in E; moreover, from the first relations in (3.27) and (3.28), we deduce that

$$\begin{aligned} \dfrac{\partial _1 L_1(\theta )}{\lambda +\eta } - \partial _2 L_2(\theta ) + F_2(\theta ,R) - \dfrac{F_1(\theta ,r)}{\lambda +\eta }>0. \end{aligned}$$
(3.36)

From (3.35) we thus conclude that

$$\begin{aligned} \dfrac{\rho _1}{\rho _2}\le \lambda +\eta . \end{aligned}$$
(3.37)

In an analogous way, taking into account the second relations in (3.27) and (3.28), it is possible to prove that

$$\begin{aligned} \dfrac{\rho _1}{\rho _2}\ge \lambda -\eta . \end{aligned}$$
(3.38)

From (3.34), (3.37) and (3.38) we deduce the invariance of the set E with respect to the radial components.

Part 3. Invariance with respect to the angular components. We have to show that, if \((\bar{\theta },r)\in E\) then \(\Vert \bar{u} - \bar{\omega }\Vert \le \Theta \), where u is given in (3.19). By the definition of the metric on \(\mathbb {T}^{2}\) in (3.20) and the choice \(\Theta <\pi \), it is enough to work on the covering space and to prove that for a suitable lifting (3.19) we have \( \Vert u - \omega \Vert \le \Theta \), with \(\theta \in {\mathbb R}^{2}\) such that \(\Vert \theta -\omega \Vert \le \Theta \), where these last two norms are Euclidean in the covering space \({\mathbb R}^{2}\) of \(\mathbb {T}^{2}\). As already announced just before the statement of the theorem, the choice \( n_{1}=n_{2}=0 \) in (3.19) will work here.

Let us split the set E into the following two subsets

$$\begin{aligned} E_{1} = \left\{ (\bar{\theta },r)\in E:\ \Vert \bar{\theta }-\bar{\omega }\Vert \le \dfrac{\Theta }{2} \right\} ,\quad E_{2} = \left\{ (\bar{\theta },r)\in E:\ \dfrac{\Theta }{2}\le \Vert \bar{\theta }-\bar{\omega }\Vert \le \Theta \right\} . \end{aligned}$$

If \((\bar{\theta },r)\in E_{1}\), then, using the first equation in (3.19), with \(n_{1}=n_{2}=0\), and also (3.31), (3.32) and (3.33), we deduce that

$$\begin{aligned} \Vert u - \omega \Vert \le \Vert \theta - \omega \Vert +\frac{1}{R} \Vert L(\theta )\Vert +\dfrac{1}{R} \Vert G(\theta ,r)\Vert \le \Vert \theta -\omega \Vert + \frac{1}{R} L^* + \frac{1}{R} L^* \le \frac{\Theta }{2}+\frac{2L^*}{R}\le \Theta . \end{aligned}$$
(3.39)

On the other hand, if \((\bar{\theta },r)\in E_{2}\), we use (3.29) and write:

$$\begin{aligned} \begin{aligned} u - \omega&= B (\theta - \omega ) + \left[ \begin{array}{c} \dfrac{\alpha _{1}(\theta )}{r_{1}} + \dfrac{G_{1}(\theta ,r)}{r_{1}\Vert \theta -\omega \Vert } \\ \dfrac{\alpha _{2}(\theta )}{r_{2}} + \dfrac{G_{2}(\theta ,r)}{r_{2}\Vert \theta -\omega \Vert } \end{array} \right] \Vert \theta -\omega \Vert , \end{aligned} \end{aligned}$$

where the matrix B is given by

$$\begin{aligned} B = \left( \begin{array}{cc} 1+\partial _{1}L_1(\omega )/r_1 &{} \partial _{2}L_1(\omega )/r_1 \\ \partial _{1}L_2(\omega )/r_2 &{} 1 +\partial _{2}L_2(\omega )/r_2 \end{array}\right) \end{aligned}$$

and has the form (3.3) with \( \epsilon =(1/r_{1},1/r_{2}) \). Using (3.30) and (3.32) we deduce that

$$\begin{aligned} \Vert u-\omega \Vert \le \Vert B\Vert _{2}\Vert \theta -\omega \Vert + \left( \Vert \alpha (\theta )\Vert \Vert \epsilon \Vert +\frac{2\Vert G(\theta ,r)\Vert }{\Theta }\Vert \epsilon \Vert \right) \Vert \theta -\omega \Vert \le \left( \Vert B\Vert _{2}+\frac{a_{0}}{2}\Vert \epsilon \Vert \right) \Theta . \end{aligned}$$

Now, \((\bar{\theta },r)\in E\) implies that \(\epsilon =(1/r_1,1/r_2)\in C_{\epsilon _0,\eta }\), see (3.4), and we can use Lemma 3.2 to obtain that \(\Vert B\Vert _{2}\le (1-a_{0}\Vert \epsilon \Vert /2)\) and conclude that \( \Vert u-\omega \Vert \le \Theta \). \(\square \)

Now, let \((\theta _0,r_0)\in E_{R,\Theta ,\lambda ,\eta }\), with \(E_{R,\Theta ,\lambda ,\eta }\) given by Theorem 3.3; since \(E_{R,\Theta ,\lambda ,\eta }\) is positively invariant, we can recursively define

$$\begin{aligned} (\theta _{n+1},r_{n+1})=f(\theta _n,r_n) \in E_{R,\Theta ,\lambda ,\eta },\quad \forall \ n\ge 0. \end{aligned}$$

From (3.34) we know that

$$\begin{aligned} (r_1)_i\ge (r_0)_i+\dfrac{\gamma _i}{2} ,\quad i=1,2, \end{aligned}$$

and iterating we infer that

$$\begin{aligned} (r_n)_i\ge (r_0)_i+ n\dfrac{\gamma _i}{2},\quad i=1,2,\quad n\ge 1. \end{aligned}$$

This relation is sufficient to prove the final result of this section.

Theorem 3.4

In the same setting of Theorem 3.3, for every \( (\theta _0,r_0)\in E_{R,\Theta ,\lambda ,\eta }\) we have

$$\begin{aligned} \lim _{n\rightarrow +\infty } (r_n)_i=+\infty , \quad i=1, 2, \end{aligned}$$

where \((\theta _{n+1},r_{n+1})=f(\theta _n,r_n)\), for every \(n\ge 0\).

Remark 3.5

We observe that, in the case of a one-to-one map f as above, an analogous result can be proved when \(JL(\omega )\) is a \(\mathcal {D}^-\)-matrix; indeed, in this situation there exist \(R>0\), \(0<\Theta < \pi \), \(\lambda >0\) and \( 0< \eta < \lambda \) such that:

$$\begin{aligned} f^{-1}(E_{R,\Theta ,\lambda ,\eta })\subset E_{R,\Theta ,\lambda ,\eta }. \end{aligned}$$

Then, for every \((\theta _0,r_0)\in E_{R,\Theta ,\lambda ,\eta }\) it is possible to define

$$\begin{aligned} (\theta _{n-1},r_{n-1})=f(\theta _{n},r_{n}), \end{aligned}$$

for every \(n\le 0\), and we have

$$\begin{aligned} \lim _{n\rightarrow -\infty } (r_n)_i=+\infty , \quad i=1, 2. \end{aligned}$$

4 The Main Result and Some Corollaries

In this section we apply the theory developed in Sect. 3 in order to prove our main result, dealing with the existence of unbounded solutions to the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}_1+a_1x_1^+-b_1x^-_1+\phi _1(x_2)=p_1(t)\\ \ddot{x}_2+a_2\,x_2^+-b_2\,x^-_2+\phi _2(x_1)=p_2(t). \end{array}\right. } \end{aligned}$$
(4.1)

We recall that, for \(i=1,2\), we are assuming the resonance condition

$$\begin{aligned} \dfrac{1}{\sqrt{a_i}}+\dfrac{1}{\sqrt{b_i}}=\dfrac{2}{n}, \quad \text { for } \text { some } n \in \mathbb {N}. \end{aligned}$$
(4.2)

Moreover, the function \(p_i: \mathbb {R} \rightarrow \mathbb {R}\) is continuous and \(2\pi \)-periodic and the function \(\phi _i: \mathbb {R} \rightarrow \mathbb {R}\) is locally Lipschitz continuous and bounded, with

$$\begin{aligned} \phi _i(-\infty )=-\phi _i(+\infty ). \end{aligned}$$
(4.3)

In this setting, and recalling the definition of the function L given in (2.25)-(2.28), the following result holds true.

Theorem 4.1

Assume conditions (4.2) and (4.3); moreover, suppose that there exists \(\omega \in \mathbb {R}^2\) such that \(L(\omega ) = 0\) and \(JL(\omega )\) is a \(\mathcal {D}^+\)-matrix. Then, there exists an infinite measure set \(E\subset {{\mathbb R}}^2\times {{\mathbb R}}^2\) such that

$$\begin{aligned} \lim _{t\rightarrow +\infty } (|x_i(t)|^2+|x'_i(t)|^2) =+\infty , \qquad i=1,2, \end{aligned}$$
(4.4)

for every solution x of (4.1) such that \((x(0),x'(0))\in E\).

Proof

The result follows from an application of Theorem 3.4, taking into account the fact that, from (2.26), the Poincaré map associated with (4.1) is of the form (3.19), with (2.27) implying (3.22).

More precisely, let \(E\subset {{\mathbb R}}^2\times {{\mathbb R}}^2\) be the set corresponding, via action-angle coordinates, to the set \(E_{R,\Theta ,\omega ,\lambda ,\eta }\) given in the statement of Theorem 3.4 and let x be a solution of (4.1) such that \((x(0),x'(0))\in E\). Then, from Theorem 3.4 we infer that

$$\begin{aligned} \lim _{k\rightarrow +\infty } (|x_i(2k\pi )|^2+|x'_i(2k\pi )|^2) =+\infty . \end{aligned}$$

The thesis (4.4) follows from this relation and an application of Gronwall’s lemma (see e.g. [2, Proof of Th. 41]), taking into account the boundedness of \(\phi _i\), for \(i=1,2\). \(\square \)

Remark 4.2

According to Remark 3.5, an analogous result for \(t\rightarrow -\infty \) can be proved when \(JL(\omega )\) is a \(\mathcal {D}^-\)-matrix.

In the rest of the section, we discuss some concrete situations in which the abstract condition on the zeros of the function L is verified, thus providing more explicit corollaries of Theorem 4.1, depending on the structure of the set of zeroes of the functions \(\Phi _i\), \(i=1,2\), defined in (2.25).

The first situation we deal with is the one in which both \(\Phi _1\) and \(\Phi _2\) have a simple zero (in the scalar setting, this situation was the one treated by [2, Th. 4.1]). More precisely, we assume that there exists \(\omega ^* = (\omega ^*_1,\omega ^*_2) \in \mathbb {R}^2\) such that

$$\begin{aligned} \Phi _1(\omega ^*_1)=\Phi _2(\omega ^*_2)=0, \qquad \Phi '_i(\omega ^*_i) < 0, \quad i=1,2. \end{aligned}$$
(4.5)

Under this assumption, the following result holds true.

Corollary 4.3

Assume conditions (4.2), (4.3) and (4.5). Then, there exists \(\phi ^*=\phi ^*(a_1,a_2,p_1,p_2)>0\) such that, for every functions \(\phi _i\) with \(|\phi _i(+\infty )|<\phi ^*\) (\(i=1,2\)), there exists an infinite measure set \(E\subset {{\mathbb R}}^2\times {{\mathbb R}}^2\) such that

$$\begin{aligned} \lim _{t\rightarrow +\infty } (|x_i(t)|^2+|x'_i(t)|^2) =+\infty , \qquad i=1,2, \end{aligned}$$

for every solution x of (4.1) such that \((x(0),x'(0))\in E\).

Proof

Let us observe that, in view of Theorem 4.1 it is sufficient to prove that, under the given assumptions, there exist \(\omega \in {{\mathbb R}}^2\) such that \(L(\omega )=0\) and \(JL(\omega )\) is a \(\mathcal {D}^+\)-matrix.

Let us first recall, from (2.25), that we have

$$\begin{aligned} L_i(\theta )=\Phi _i(\theta _i)+\gamma _i n\phi _i(+\infty ) (\Lambda _i (\theta _{i}-\theta _{i+1})-\alpha _i),\quad \forall \ \theta \in {{\mathbb R}}^2, \end{aligned}$$
(4.6)

where \(\Lambda _i\) is defined in (2.9). Let us define \(H:{{\mathbb R}}^2\times {{\mathbb R}}^2\rightarrow {{\mathbb R}}^2\) by

$$\begin{aligned} H(\theta ,v)=(\Phi _1(\theta _1)+\gamma _1 n v_1 (\Lambda _1 (\theta _{1}-\theta _{2})-\alpha _1), \Phi _2(\theta _2)+\gamma _2 n v_2 (\Lambda _2 (\theta _{2}-\theta _{1})-\alpha _2)),\quad \forall \ \theta \in {{\mathbb R}}^2,\ v\in {{\mathbb R}}^2. \end{aligned}$$
(4.7)

From (4.5) we immediately infer that

$$\begin{aligned} H(\omega ^*_1,\omega ^*_2,0,0)=0 \end{aligned}$$

and

$$\begin{aligned} J_\theta H(\omega ^*_1,\omega ^*_2,0,0)=\left( \begin{array}{cc} \Phi '_1(\omega ^*_1)&{}0\\ &{}\\ 0&{} \Phi '_2(\omega ^*_2) \end{array} \right) \ne 0. \end{aligned}$$

Hence, by the implicit function theorem, we deduce that there exists \(\hat{\phi }>0\) such that for every \((\phi _1(+\infty ),\phi _2(+\infty ))\in {{\mathbb R}}^2\) with \(|\phi _i(+\infty )|<\hat{\phi }\), \(i=1,2\), there exists \(\omega =\omega (\phi _1(+\infty ),\phi _2(+\infty )) \in \mathbb {R}^2\) near \(\omega ^*\) such that

$$\begin{aligned} L(\omega )=0. \end{aligned}$$

Now, let us observe that

$$\begin{aligned} J L(\omega )=\left( \begin{array}{cc} \Phi '_1(\omega _1)+ \gamma _1 \phi _1(+\infty ) \Sigma _1(\omega _1 -\omega _2) &{} - \gamma _1 \phi _1(+\infty ) \Sigma _1(\omega _1-\omega _2) \\ &{}\\ - \gamma _2 \phi _2(+\infty ) \Sigma _2(\omega _2-\omega _1) &{} \Phi '_2(\omega _2) + \gamma _2 \phi _2(+\infty ) \Sigma _2(\omega _2-\omega _1) \end{array} \right) , \end{aligned}$$

where \(\Sigma _i\) is given in (2.13). The continuity of \(\omega \) as function of \((\phi _1(+\infty ),\phi _2(+\infty ))\), ensured by the implicit function theorem, implies that

$$\begin{aligned} \lim _{|(\phi _1(+\infty ),\phi _2(+\infty ))|\rightarrow 0^+} J L(\omega )=\left( \begin{array}{cc} \Phi '_1(\omega ^*_1)&{}0\\ &{}\\ 0&{} \Phi '_2(\omega ^*_2) \end{array} \right) ; \end{aligned}$$

by (4.5) the limit matrix is a \(\mathcal {D}^+\)-matrix. As a consequence, there exists \(\phi ^* \in (0,\hat{\phi })\) such that for every \((\phi _1(+\infty ),\phi _2(+\infty ))\in {{\mathbb R}}^2\) with \(|\phi _i(+\infty )|<\phi ^*\) the matrix \(J L(\omega )\) is a \(\mathcal {D}^+\)-matrix, as well. The result is then proved. \(\square \)

Remark 4.4

A dual result, ensuring the existence of solutions unbounded in the past, could be proved when (4.5) is replaced by

$$\begin{aligned} \Phi _1(\omega ^*_1)=\Phi _2(\omega ^*_2)=0, \qquad \Phi '_i(\omega ^*_i) > 0, \quad i=1,2. \end{aligned}$$

We omit the details for briefness.

Remark 4.5

Let us analyze the result of Corollary 4.3 in the symmetric linear case \(a_i=b_i=n^2\), \(i=1, 2\). In this situation, in the recent paper [3] the existence of unbounded solutions has been proved under the assumption

$$\begin{aligned} 4|\phi _i(+\infty )| < |{\widehat{p}}_{i,n}|^2,\quad i=1,2, \end{aligned}$$
(4.8)

where

$$\begin{aligned} {\widehat{p}}_{i,n}=\int _{0}^{2\pi } p_i(t)e^{int}\,dt \end{aligned}$$
(4.9)

(see Theorem 3.1 in [3]). The assumption \(|\phi _i(+\infty )|<\phi ^*\) (\(i=1,2\)), with \(\phi ^*=\phi ^*(a_1,b_1,p_1,p_2)\), in Corollary 4.3 is then on the same spirit of (4.8).

Let us now focus on the situation where the function \(\Phi _1\) (or \(\Phi _2\)) is identically zero, i.e.

$$\begin{aligned} \Phi _1(\theta _1)=0,\quad \forall \ \theta _1\in {\mathbb R}. \end{aligned}$$
(4.10)

Incidentally, let us observe that in the linear symmetric case \(a_1=b_1=n^2\) assumption (4.10) corresponds to the case when the number \({\widehat{p}}_{1,n}\) in (4.9) is zero. Instead, in the asymmetric case \(a_1\ne b_1\), condition (4.10) is more tricky to be checked. However, some examples in which it holds can be provided. For instance, if \(a_{1}\) satisfies

$$\begin{aligned} \frac{\sqrt{a_{1}}}{n}=\frac{s}{1+2k} \qquad \text {for some } s,k\in \mathbb {N} \text { and } s>k, \end{aligned}$$
(4.11)

then the Fourier coefficient \(c_{s,1}\) of \(C_{1}\) vanishes (see (2.6)), and (4.10) holds when \(p_1(t)=\cos snt\).

For the sake of brevity and clarity, we present here just a couple of corollaries in which (4.10) is assumed. In the first we suppose that \(a_{2}\) is such that

$$\begin{aligned} c_{r,2}\ne 0 \quad \text {for some } r\in \mathbb {N}, \end{aligned}$$
(4.12)

and that

$$\begin{aligned} p_2(t)=\mu \cos rnt,\quad \forall \ t\in {\mathbb R}, \end{aligned}$$
(4.13)

with \(\mu >0\).

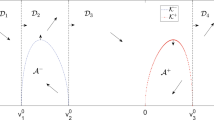
Corollary 4.6

Let \(a_i, b_i > 0\) satisfy, for \(i=1,2\), assumption (4.2); moreover, suppose that

$$\begin{aligned} (a_{1},a_{2})\in \mathcal {R}, \end{aligned}$$
(4.14)

where \(\mathcal {R}\) is defined in (2.14), and that (4.12) is fulfilled. Finally, assume that conditions (4.3), (4.10) and (4.13) are satisfied. Then, for every \(\phi _1(+\infty )\ne 0\) and for every \(\phi _2(+\infty )\in {\mathbb R}\) there exists \(\mu ^*>0\) such that for every \(\mu >\mu ^*\) there exist two infinite measure sets \(E^\pm \subset {{\mathbb R}}^2\times {{\mathbb R}}^2\) such that:

  • for every solution x of (4.1) such that \((x(0),x'(0))\in E^+\),

    $$\begin{aligned} \lim _{t\rightarrow +\infty } (|x_i(t)|^2+|x'_i(t)|^2) =+\infty , \qquad i=1,2, \end{aligned}$$

  • for every solution x of (4.1) such that \((x(0),x'(0))\in E^-\)

    $$\begin{aligned} \lim _{t\rightarrow -\infty } (|x_i(t)|^2+|x'_i(t)|^2) =+\infty , \qquad i=1,2. \end{aligned}$$

We observe that it is possible to find situations in which Corollary 4.6 applies. Indeed, let us first notice that Lemma 2.2 implies that (4.14) holds if \((a_{1},a_{2})\) is close to \((n^{2},n^{2})\). This happens, for instance if \(a_{1}\) satisfies (4.11) with \( s=2k \) and k large enough, and if \(\sqrt{a_{2}}\) is irrational and close to n. With these choices (4.10) holds with \(p_{1}(t)=\cos (2knt)\), while (4.12) is trivially satisfied (see (2.6)).

Proof

Let us first notice that, from (2.25) and (4.13), recalling the Fourier expansion of \(C_2\) given in (2.5), we obtain

$$\begin{aligned} \Phi _2(\theta _2)=-\dfrac{\gamma _2}{2} \pi \mu c_{r,2} \cos r \theta _2,\quad \forall \ \theta _2\in {\mathbb R}. \end{aligned}$$
(4.15)

As a consequence, recalling (4.10), we obtain

$$\begin{aligned} \begin{aligned} L_1(\theta )&= \gamma _1 n\phi _1(+\infty ) (\Lambda _1 (\theta _{1}-\theta _{2})-\alpha _1)\\ L_2(\theta )&= -\dfrac{\gamma _2}{2} \pi \mu c_{r,2} \cos r \theta _2+\gamma _2 n\phi _2(+\infty ) (\Lambda _2 (\theta _{2}-\theta _{1})-\alpha _2), \end{aligned} \end{aligned}$$
(4.16)

for every \(\theta \in {{\mathbb R}}^2\).

Now, let us look for solutions of \(L(\theta )=0\); from the relation \(L_1(\theta )=0\), recalling that \(\phi _1(+\infty )\ne 0\), we deduce

$$\begin{aligned} \Lambda _1 (\theta _{1}-\theta _{2})=\alpha _1. \end{aligned}$$
(4.17)

From Lemma 2.1, taking into account (4.14), we infer that there exists \(\Lambda _1^* \in (0,\pi )\) such that

$$\begin{aligned} \begin{array}{l} \Lambda _1(t)=\alpha _1 \quad \Longleftrightarrow \quad t=\pm \Lambda _1^*+2m\pi ,\ m\in \mathbb {Z}\\ \\ \text {sgn}(\Lambda '_1(\pm \Lambda _1^*))=\mp 1. \end{array} \end{aligned}$$
(4.18)

In particular, we choose \(m=0\); then, from (4.17) and (4.18) we obtain

$$\begin{aligned} \theta _1-\theta _2=\pm \Lambda _1^*. \end{aligned}$$
(4.19)

Replacing the last equality in the expression of \(L_2\) in (4.16) and recalling that \(\Lambda _2\) is even and \(2\pi \)-periodic, the equation \(L_2(\theta )=0\) reduces to

$$\begin{aligned} -\pi \mu c_{r,2} \cos r \theta _2+2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)=0, \end{aligned}$$
(4.20)

i.e.

$$\begin{aligned} \cos r \theta _2 = \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}}. \end{aligned}$$
(4.21)

Let now set

$$\begin{aligned} \hat{\mu }= \left| \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi c_{r,2}}\right| ; \end{aligned}$$
(4.22)

then, for every \(\mu >\hat{\mu }\) the equation (4.21) can be solved and we obtain

$$\begin{aligned} \theta _2 = \dfrac{1}{r} \left( \pm \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}} + 2h\pi \right) ,\quad h\in \mathbb {Z}. \end{aligned}$$
(4.23)

Choosing \(h = 0\), we then conclude that, for every \(\mu >\hat{\mu }\), the equation \(L(\theta )=0\) has the four solutions

$$\begin{aligned} \omega ^{\pm ,1}_{\mu }= & {} \left( \Lambda _1^* + \dfrac{1}{r} \left( \pm \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}}\right) ,\right. \\&\left. \dfrac{1}{r} \left( \pm \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}} \right) \right) \end{aligned}$$

and

$$\begin{aligned} \omega ^{\pm ,2}_{\mu }= & {} \left( -\Lambda _1^* +\dfrac{1}{r} \left( \pm \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}} \right) ,\right. \\&\left. \dfrac{1}{r} \left( \pm \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}}\right) \right) . \end{aligned}$$

In order to apply Theorem 4.1, we claim that one of the above four solutions, to be named \(\omega ^+\), is such that \(JL(\omega ^+)\) is a \(\mathcal {D}^+\)-matrix and another one, to be named \(\omega ^-\), is such that \(JL(\omega ^-)\) is a \(\mathcal {D}^-\)-matrix. To do this, recalling (4.16) and the fact that \(\Lambda '_i=\Sigma _i/n\) is \(2\pi \)-periodic and odd, we observe that

$$\begin{aligned} \begin{aligned} \partial _1 L_1 (\omega ^{\pm ,i}_{\mu })=&(-1)^{i+1} \gamma _1 \phi _1(+\infty ) \Sigma _1 (\Lambda _1^*)\\ \partial _2 L_1 (\omega ^{\pm ,i}_{\mu })=&(-1)^{i} \gamma _1 \phi _1(+\infty ) \Sigma _1 (\Lambda _1^*)\\ \partial _1 L_2 (\omega ^{\pm ,i}_{\mu })=&(-1)^{i} \gamma _2 \phi _2(+\infty ) \Sigma _2 (\Lambda _1^*)\\ \partial _2 L_2 (\omega ^{\pm ,i}_{\mu })=&\pm \dfrac{\gamma _2}{2} \pi \mu c_{r,2} r \sin \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}} +\displaystyle (-1)^{i+1} \gamma _2 \phi _2(+\infty ) \Sigma _2 (\Lambda _1^*), \end{aligned} \end{aligned}$$
(4.24)

for \(i=1,2\). Now, since \(\phi _1(+\infty )\ne 0\) and recalling (4.18), we have

$$\begin{aligned} {\text {sgn}} (\partial _1 L_{1} (\omega ^{\pm ,i}_{\mu })) = (-1)^{i} {\text {sgn}} (\phi _1(+\infty )); \end{aligned}$$
(4.25)

moreover, there exists \(\check{\mu }\ge \hat{\mu }\) such that for every \(\mu >\check{\mu }\) we have

$$\begin{aligned} {\text {sgn}} (\partial _2 L_{2} (\omega ^{\pm ,i}_{\mu })) = \pm {\text {sgn}} (c_{r,2}). \end{aligned}$$
(4.26)

Hence, for \(\mu >\check{\mu }\), the choice of \(\omega ^{\pm ,i}_{\mu }\) has to be made according to the signs of \(\phi _1(+\infty )\) and \(c_{r,2}\). For the sake of briefness, we discuss the case \(\phi _1(+\infty )>0\) and \(c_{r,2}>0\), the other ones being similar. We set \(\omega ^+= \omega ^{-,1}_{\mu }\) and \(\omega ^-= \omega ^{+,2}_{\mu }\); hence, by construction, \(JL(\omega ^+)\) and \(JL (\omega ^-)\) satisfy the sign conditions on the diagonal coefficients in order to be a \(\mathcal {D}^\pm \)-matrix. As far as the third condition in Definition 3.1 is concerned, we have that

$$\begin{aligned} \begin{aligned} \partial _1 L_{1} (\omega ^\pm )\, \partial _1 L_{2} (\omega ^\pm ) +&\partial _2 L_{1} (\omega ^\pm )\, \partial _2 L_{2} (\omega ^\pm )= -2 \gamma _1 \gamma _2 \phi _1(+\infty ) \phi _2(+\infty ) \Sigma _1 (\Lambda _1^*) \Sigma _2 (\Lambda _1^*)\\&+ \gamma _1 \dfrac{\gamma _2}{2} \pi \mu c_{r,2} rn \sin \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}} \phi _1(+\infty ) \Sigma _1 (\Lambda _1^*) \end{aligned} \end{aligned}$$
(4.27)

and

$$\begin{aligned} \begin{aligned} 2 \partial _1 L_{1} (\omega ^\pm )\, \partial _2 L_{2} (\omega ^\pm )=&2 \gamma _1 \gamma _2 \phi _1(+\infty ) \phi _2(+\infty ) \Sigma _1 (\Lambda _1^*) \Sigma _2 (\Lambda _1^*) \\&- \gamma _1 \gamma _2 \pi \mu c_{r,2} rn \sin \arccos \dfrac{2 n\phi _2(+\infty ) (\Lambda _2 (\Lambda _1^*)-\alpha _2)}{\pi \mu c_{r,2}} \phi _1(+\infty ) \Sigma _1 (\Lambda _1^*). \end{aligned} \end{aligned}$$
(4.28)

Hence, there exists \(\mu ^*\ge \check{\mu }\) such that for every \(\mu >\mu ^*\) the third condition in Definition 3.1 is satisfied; hence the values \(\omega ^\pm \) are such that \(JL(\omega ^\pm )\) is a \(\mathcal {D}^\pm \) matrix. The thesis then follows from an application of Theorem 4.1. \(\square \)

As a last application, we discuss the case when the oscillators are symmetric, i.e. \(a_i=b_i = n^2\) for \(i=1,2\), and (4.10) holds true; as already observed, this is equivalent to the assumption

$$\begin{aligned} \widehat{p}_{1,n}=0, \end{aligned}$$
(4.29)

where \(\widehat{p}_{1,n}\) is as in (4.9). Let us observe that this situation is not covered by the results in [3].

Corollary 4.7

Let \(a_i=b_i=n^2\), for \(i=1,2\), and suppose that conditions (4.3) and (4.29) are satisfied.

Then, for every \(\phi _1(+\infty )\ne 0\) and for every \(\phi _2(+\infty )\in {\mathbb R}\) such that

$$\begin{aligned} |\phi _2(+\infty )| < \dfrac{3}{16} |\widehat{p}_{2,n}|, \end{aligned}$$
(4.30)

with \({\widehat{p}}_{2,n}\) as in (4.9), there exist two infinite measure sets \(E^\pm \subset {{\mathbb R}}^2\times {{\mathbb R}}^2\) such that:

  • for every solution x of (4.1) such that \((x(0),x'(0))\in E^+\),

    $$\begin{aligned} \lim _{t\rightarrow +\infty } (|x_i(t)|^2+|x'_i(t)|^2) =+\infty , \qquad i=1,2, \end{aligned}$$

  • for every solution x of (4.1) such that \((x(0),x'(0))\in E^-\)

    $$\begin{aligned} \lim _{t\rightarrow -\infty } (|x_i(t)|^2+|x'_i(t)|^2) =+\infty , \qquad i=1,2. \end{aligned}$$

Proof

First of all, let us observe that in this situation the functions \(C_i\) and \(\Lambda _i\) in (2.4) and (2.9) are given by

$$\begin{aligned} C_i(t)=\cos n t,\quad \Lambda _i(t)=\dfrac{2}{n}\cos t,\quad \forall \ t\in {\mathbb R}, \end{aligned}$$
(4.31)

respectively, while the number \(\alpha _i\) in (2.11) is zero. Moreover, the function \(\Phi _{2}\) in (2.25) becomes

$$\begin{aligned} \Phi _{2}(u)=-\dfrac{1}{\sqrt{2n}} \int _0^{2\pi } \cos (nt+u) p_{2}(t)dt,\quad \forall \ u\in {\mathbb R}; \end{aligned}$$
(4.32)

this expression can be written as

$$\begin{aligned} \Phi _{2}(u)=-\dfrac{1}{\sqrt{2n}}\, |\widehat{p}_{2,n}| \cos (u+\psi _{2}),\quad \forall \ u\in {\mathbb R}, \end{aligned}$$
(4.33)

for some \(\psi _2\in {\mathbb R}\).

From (4.31), (4.32), (4.33) and the assumption on \(\widehat{p}_{1,n}\) we deduce that

$$\begin{aligned} \begin{array}{ll} \displaystyle L_1 (\theta )=2\sqrt{\frac{2}{n}} \phi _1(+\infty ) \cos (\theta _1-\theta _2) \\ \\ \displaystyle L_2 (\theta )=-\dfrac{1}{\sqrt{2n}}\, |\widehat{p}_{2,n}| \cos (\theta _2+\psi _2)+2\sqrt{\frac{2}{n}} \phi _2(+\infty ) \cos (\theta _2-\theta _1), \end{array} \end{aligned}$$
(4.34)

for every \(\theta \in {{\mathbb R}}^2\).

Recalling that \(\phi _1(+\infty )\ne 0\), we can solve the equation \(L_1(\theta )=0\) to obtain

$$\begin{aligned} \theta _1=\theta _2 \pm \dfrac{\pi }{2} +2m\pi ,\quad m\in \mathbb {Z}; \end{aligned}$$
(4.35)

as a consequence the equation \(L_2 (\theta )=0\) reduces to

$$\begin{aligned} |\widehat{p}_{2,n}| \cos (\theta _2+\psi _2)=0. \end{aligned}$$
(4.36)

We now observe that assumption (4.30) implies that \(\widehat{p}_{2,n}\ne 0\); hence, from (4.36) we infer that

$$\begin{aligned} \theta _2=-\psi _2 \pm \dfrac{\pi }{2} +2h\pi ,\quad h\in \mathbb {Z}. \end{aligned}$$
(4.37)

Choosing in particular \(m = h = 0\), we conclude that the equation \(L(\theta )=0\) has the four solutions

$$\begin{aligned} \begin{array}{l} \displaystyle \omega ^{\pm ,1} = \left( -\psi _2 +\dfrac{\pi }{2} \pm \dfrac{\pi }{2} , -\psi _2 \pm \dfrac{\pi }{2} \right) \in \mathbb {R}^2, \\ \\ \displaystyle \omega ^{\pm ,2} = \left( -\psi _2 -\dfrac{\pi }{2} \pm \dfrac{\pi }{2} , -\psi _2 \pm \dfrac{\pi }{2} \right) \in \mathbb {R}^2. \end{array} \end{aligned}$$
(4.38)

We now claim that one of the above four solutions, to be named \(\omega ^+\), is such that \(JL(\omega ^+)\) is a \(\mathcal {D}^+\)-matrix and another one, to be named \(\omega ^-\), is such that \(JL(\omega ^-)\) is a \(\mathcal {D}^-\)-matrix. To see this, let us observe that, from (4.38),

$$\begin{aligned} \begin{aligned} \partial _1 L_1 (\omega ^{\pm ,i})&= \partial _1 L_1 (\theta )_{\vert \theta = \omega ^{\pm ,i}}= -2\sqrt{\frac{2}{n}} \phi _1(+\infty ) \sin (\theta _1-\theta _2)_{\vert \theta = \omega ^{\pm ,i}}= (-1)^{i} 2\sqrt{\frac{2}{n}} \phi _1(+\infty ) \\ \partial _2 L_1 (\omega ^{\pm ,i})&= \partial _2 L_1 (\theta )_{\vert \theta = \omega ^{\pm ,i}} = 2\sqrt{\frac{2}{n}} \phi _1(+\infty ) \sin (\theta _1-\theta _2)_{\vert \theta = \omega ^{\pm ,i}} = (-1)^{i-1} 2\sqrt{\frac{2}{n}} \phi _1(+\infty ) \\ \partial _1 L_2 (\omega ^{\pm ,i})&= \partial _1 L_2 (\theta )_{\vert \theta = \omega ^{\pm ,i}} = 2\sqrt{\frac{2}{n}} \phi _2(+\infty ) \sin (\theta _2-\theta _1)_{\vert \theta = \omega ^{\pm ,i}} = (-1)^{i} 2\sqrt{\frac{2}{n}} \phi _2(+\infty ) \\ \partial _2 L_2 (\omega ^{\pm ,i})&= \partial _2 L_2 (\theta )_{\vert \theta = \omega ^{\pm ,i}} = \dfrac{1}{\sqrt{2n}} |\widehat{p}_{2,n}| \sin (\theta _2+\psi _2) -2\sqrt{\frac{2}{n}} \phi _2(+\infty ) \sin (\theta _2-\theta _1)_{\vert \theta = \omega ^{\pm ,i}} \\&= \pm \dfrac{1}{\sqrt{2n}} |\widehat{p}_{2,n}| + (-1)^{i-1} 2\sqrt{\frac{2}{n}} \phi _2(+\infty ), \end{aligned} \end{aligned}$$
(4.39)

for \(i=1,2\). Focusing for the sake of briefness on the case \(\phi _1(+\infty )>0\), we obtain from (4.30) that

$$\begin{aligned} \begin{aligned} {\text {sgn}} (\partial _1 L_{1} (\omega ^{-,1}))\cdot {\text {sgn}} (\partial _2 L_{2} (\omega ^{-,1}))>0\\ {\text {sgn}} (\partial _1 L_{1} (\omega ^{+,2}))\cdot {\text {sgn}} (\partial _2 L_{2} (\omega ^{+,2})) >0. \end{aligned} \end{aligned}$$
(4.40)

Setting \(\omega ^+ = \omega ^{+,2}\) and \(\omega ^-=\omega ^{-,1}\), since

$$\begin{aligned} \partial _1 L_{1} (\omega ^\pm )\, \partial _1 L_{2} (\omega ^\pm )+\partial _2 L_{1} (\omega ^\pm )\, \partial _2 L_{2} (\omega ^\pm )=\displaystyle \frac{1}{n}\left( 16\phi _1(+\infty )\phi _2(+\infty ) -2|\widehat{p}_{2,n}|\phi _1(+\infty )\right) \end{aligned}$$
(4.41)

and

$$\begin{aligned} 2 \partial _1 L_{1} (\omega ^\pm )\, \partial _2 L_{2} (\omega ^\pm )=\frac{1}{n}\left( -16\phi _1(+\infty )\phi _2(+\infty ) +4|\widehat{p}_{2,n}|\phi _1(+\infty )\right) , \end{aligned}$$
(4.42)

from the same assumption (4.30) we deduce that

$$\begin{aligned} |\partial _1 L_{1} (\omega ^\pm )\, \partial _1 L_{2} (\omega ^\pm )+\partial _2 L_{1} (\omega ^\pm )\, \partial _2 L_{2} (\omega ^\pm )|<2 \partial _1 L_{1} (\omega ^\pm )\, \partial _2 L_{2} (\omega ^\pm ) \end{aligned}$$
(4.43)

as well. From (4.40) and (4.43) we conclude that \(JL(\omega ^\pm )\) is a \(\mathcal {D}^\pm \)-matrix. The thesis then follows from an application of Theorem 4.1. \(\square \)