Skip to main content
Springer Nature Link
Log in

Authenticable Quantum Scheme for Secret Sharing Based on Local Distinguishability

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

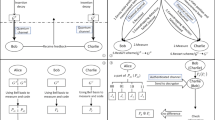
The main defects of the existing quantum secret sharing schemes are as follows: (1) The identity of the secret sender cannot be confirmed. Receivers of shared secret information may be vulnerable to Trojan attacks; (2) If a malicious attacker Eve impersonates the identity of the receiver, she can finally obtain all the information of the secret that Alice shared; (3) In the process of secret recovery, it is necessary to transmit qubits among all participants involved in secret recovery. Sometimes, the same particle needs to be operated on by all participants to achieve secret sharing, which increases the possibility of eavesdropping and also increases the probability of errors. In this work, we proposed a quantum secret sharing scheme with authentication, the receiver performs corresponding operations on qubits of Greenberger-Horne-Zeilinger(GHZ) state based on the key string calculated by the shared identity number and random Error Correction Code(ECC), the secret sender can calculate the corresponding measurement basis(MB) through the information she has, and then inform the measurement party. This process realizes the mutual authentication between the sender and the receiver. It can protect against identity impersonation attacks, through the ECC verification, it also can resist intercept-resend attacks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Bennett, C.H., Brassard, G.: Quantum cryptography: Public key distribution and con tos5. In: Proceedings of the International Conference on Computers, Systems and Signal Processing, pp. 175–179 (1984)

  2. Blakley, G.R.: Safeguarding cryptographic keys. In: Managing Requirements Knowledge, International Workshop on, pp. 313–313. IEEE Computer Society (1979)

  3. Chen, Y.A., Zhang, A.N., Zhao, Z., Zhou, X.Q., Lu, C.Y., Peng, C.Z., Yang, T., Pan, J.W.: Experimental quantum secret sharing and third-man quantum cryptography. Phys. Rev. Lett. 95(20), 200502 (2005)

    Article  ADS  Google Scholar 

  4. Cleve, R., Gottesman, D., Lo, H.K.: How to share a quantum secret. Phys. Rev. Lett. 83(3), 648 (1999)

    Article  ADS  Google Scholar 

  5. Dou, Z., Xu, G., Chen, X.B., Niu, X.X., Yang, Y.X., Yang, Y.: Searching for optimal quantum secret sharing scheme based on local distinguishability. Quantum Inf. Process. 19(10), 1–19 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  6. Fortescue, B., Gour, G.: Reducing the quantum communication cost of quantum secret sharing. IEEE Trans. Inf. Theory 58(10), 6659–6666 (2012)

    Article  MathSciNet  Google Scholar 

  7. González-Guillén, C.E., Vasco, M.I.G., Johnson, F., del Pozo, A.L.P.: Concerning quantum identification without entanglement. arXiv:2003.12095 (2020)

  8. Hao, C., Wenping, M.: (t, n) threshold quantum state sharing scheme based on linear equations and unitary operation. IEEE Photonics J. 9(1), 1–7 (2017)

    Article  Google Scholar 

  9. Hillery, M., Bužek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59(3), 1829 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  10. Karimipour, V., Asoudeh, M.: Quantum secret sharing and random hopping: using single states instead of entanglement. Phys. Rev. A 92(3), 030301 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  11. Kogias, I., Xiang, Y., He, Q., Adesso, G.: Unconditional security of entanglement-based continuous-variable quantum secret sharing. Phys. Rev. A 95(1), 012315 (2017)

    Article  ADS  Google Scholar 

  12. Lau, H.K., Weedbrook, C.: Quantum secret sharing with continuous-variable cluster states. Phys. Rev. A 88(4), 042313 (2013)

    Article  ADS  Google Scholar 

  13. Lu, H., Zhang, Z., Chen, L.K., Li, Z.D., Liu, C., Li, L., Liu, N.L., Ma, X., Chen, Y.A., Pan, J.W.: Secret sharing of a quantum state. Phys. Rev. Lett. 117(3), 030501 (2016)

    Article  ADS  Google Scholar 

  14. Medeiros, R.A., Assis, F.M.: Zero-error capacity of a quantum channel. In: ICT (2004)

  15. Pilaram, H., Eghlidos, T.: An efficient lattice based multi-stage secret sharing scheme. IEEE Trans. Depend. Secure Comput. 14(1), 2–8 (2015)

    Google Scholar 

  16. Rahaman, R., Parker, M.G.: Quantum scheme for secret sharing based on local distinguishability. Phys. Rev. A 91(2), 022330 (2015)

    Article  ADS  Google Scholar 

  17. Schmid, C., Trojek, P., Bourennane, M., Kurtsiefer, C., Żukowski, M., Weinfurter, H.: Experimental single qubit quantum secret sharing. Phys. Rev. Lett. 95(23), 230505 (2005)

    Article  ADS  Google Scholar 

  18. Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)

    Article  MathSciNet  Google Scholar 

  19. Singh, S.K., Srikanth, R.: Generalized quantum secret sharing. Phys. Rev. A 71(1), 012328 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  20. Tavakoli, A., Herbauts, I., Żukowski, M., Bourennane, M.: Secret sharing with a single d-level quantum system. Phys. Rev. A 92(3), 030302 (2015)

    Article  ADS  Google Scholar 

  21. Tsai, C.W., Yang, C.W., Lin, J.: Multiparty mediated semi-quantum secret sharing protocol. arXiv:2102.06846 (2021)

  22. Wang, J., Li, L., Peng, H., Yang, Y.: Quantum-secret-sharing scheme based on local distinguishability of orthogonal multiqudit entangled states. Phys. Rev. A 95(2), 022320 (2017)

    Article  ADS  Google Scholar 

  23. Wang, J., Zhang, Q., Tang, C.J.: Multiparty simultaneous quantum identity authentication based on entanglement swapping. arXiv:ph/0605006(2006)

  24. Yang, Y.H., Gao, F., Wu, X., Qin, S.J., Zuo, H.J., Wen, Q.Y.: Quantum secret sharing via local operations and classical communication. Sci. Rep. 5(1), 1–9 (2015)

    Google Scholar 

  25. Yuan, H., Liu, Y.M., Pan, G.Z., Zhang, G., Zhou, J., Zhang, Z.J.: Quantum identity authentication based on ping-pong technique without entanglements. Quantum Inf. Process. 13(11), 2535–2549 (2014)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Beijing University of Technology, Beijing, China

    Xing-Lan Zhang, Li-Yu Zuo & Sheng-Lin Yin

Authors
  1. Xing-Lan Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Li-Yu Zuo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Sheng-Lin Yin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xing-Lan Zhang.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, XL., Zuo, LY. & Yin, SL. Authenticable Quantum Scheme for Secret Sharing Based on Local Distinguishability. Int J Theor Phys 60, 3396–3403 (2021). https://doi.org/10.1007/s10773-021-04896-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-021-04896-9

Keywords