1 Motivation

Terahertz radiation has been the subject of growing attention because of its unique properties: non-ionizing nature, good transmission through many non-metallic media, and the possibilities of spectral fingerprinting of various materials, including hazardous ones. THz beams are used in numerous areas, including medicine, telecommunication, and security systems. In most of the application scenarios, the information is carried by spectral distribution, therefore systems providing a linear spectral response from 0.1 to 3 THz are highly desired.

Beams with wavelengths in the range of millimeters are specularly reflected from object surfaces. Moreover, multiple reflections occur in slabs of materials and the phasing of such multiple wavefronts gives raise to Fabry-Perot (F-P) effects. For these reasons, spectral measurements of flat samples are usually compromised by the periodic attenuation function, resulting from the F-P phenomenon.

Stray reflections from flat slabs of materials can be partly suppressed by adding anti-reflection (AR) coatings [1, 2]. The traditional multi-layer approach in this case is problematic due to the small choice of feasible materials with appropriate refractive indices [3,4,5]. Brückner et al. have examined the use of TOPAS, PTFE, and HDPE materials structured with single-point diamond turning [1] and ultraprecision turning process [6] for reduced reflections. Recently, all dielectric microstructured materials have been successfully used as THz absorbers [7]. Gatesman and Hübers have validated the use of parylene films as AR layers; nevertheless, their use below 1 THz is troublesome due to problems with proper thickness [8, 9]. Recently, Neeraj et al. have proposed the use of metallic copper structures as AR for THz for the price of non-negligible amplitude attenuation [10]. In this paper, we present the use of cost-effective, dielectric 3-D printed anti-reflection coatings. The design is straightforward and the precision of additive manufacturing ensures the proper functionality for the frequency range of 0.1–0.3 THz.

2 The Test Configuration

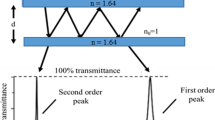
The proposed 3-D printed AR structures were tested in the straightforward configuration of a plastic slab of material illuminated at an angle of 45° with a collimated THz beam, which usually exhibits strong F-P oscillations [11].

The test configuration is shown in Fig. 1. The plastic slab with a refractive index of n and width of d is illuminated at an angle α to the normal with a single ray A 1. As a result of multiple reflections from the plastic-air interface, numerous T n rays are transmitted through the slab and simultaneously R n rays are reflected from the slab.

Fig. 1
figure 1

Ray tracing of THz beam illuminating the test plastic slab, resulting in Fabry-Perot interference

Full size image

The resultant rays are mutually coherent, therefore phase relations between subsequent rays must be established in order to assess the final reflectance and transmittance of the slab as a function of the wavelength. The following formula gives the phase delay between rays T 1 and T 2 [12]:

$$ \varDelta =4\pi \frac{n}{\lambda }d\cos \beta, $$
(1)

while the transmission of such etalon plate can be described by:

$$ {T}_e=\frac{1}{1+F{\mathrm{sin}}^2\left(\frac{\varDelta }{2}\right)}, $$
(2)

where, \( F=\frac{4R}{{\left(1-R\right)}^2} \) is the finesse and R is the reflectance of both surfaces. Figure 2 shows the theoretical transmission of the slab for different finesse values.

Fig. 2
figure 2

Theoretical transmission of a slab for four different finesse values

Full size image

Obviously, the maximal transmission occurs when the optical path difference (OPD) between subsequent transmitted rays is equal to the multitude of the wavelength.

3 Design and Fabrication of THz Anti-Reflection Coatings

The working principle of the proposed AR coating is the formation of a gradient of the refractive index at the interface between the air and the plastic slab. The precision of currently available additive manufacturing allows 3-D printing of diffractive [13, 14] and sub-wavelength structures for longer wavelengths of the THz range [15, 16]. We were able to imprint pyramid-like structures directly on top of the slab in order to form the variable distribution of the effective refractive index.

The distribution of the refractive index has been optimized according to the known methodology of W. H. Southwell [17]. The design was constrained by the precision limit of the 3-D printer, having the voxel size of 39 × 39 × 16 μm. The AR was designed as a quasi-planar, two-dimensional periodic array of pyramids with the height of h = 2 mm and spacing equal to d = 1mm, as shown in Fig. 3.

Fig. 3
figure 3

Anti-reflection coatings. a Design. b Photo. c Close-up of a one-sided AR layer. d Close-up of a two-sided AR layer

Full size image

The structures were fabricated in the selective laser sintering (SLS) [18] process in PA-12 (polyamide) material, which has the refractive index of 1.64 in the range 0.1–1 THz [19].

4 Experimental Measurements and Numerical Simulations

Terahertz time-domain spectroscopy (TDS) systems usually work in in-line mode in which the detector directly observes the emitter, with the sample mounted in between. In our case, the goniometric TDS setup depicted in Fig. 4 was used in order to characterize the spectral transmittance and reflectance of the polyamide slab. The measurements were performed in three series: without AR layers, with a one-sided AR layer, and with a two-sided AR layer. The used configuration allowed us to gather the angular distribution of energy around the measured slab in order to detect traces of higher order reflections coming e.g. from the diffraction [20]. It also enabled us to take into account the spectral and angular characteristics of the emitted THz field and its modification caused by the measured sample.

Fig. 4
figure 4

THz goniometric time-domain spectroscopy setup in reflective (upper) and transmissive mode (bottom). a Femtosecond laser. b Beam splitter. c Delay line. d Chopper. e Mirror. f Lens. g Emitter. h Sample. i Diffraction grating. j Fiber collimator. k Fiber. l Moving receiver. m Amplifier. n Lock-in

Full size image

Low-temperature-grown GaAs semi-conducting antennae illuminated by a femtosecond laser were used as the emitter and the detector. Optical paths of the two interfering beams were precisely adjusted by the mechanical delay line, controlled by a computer. The pumping beam was delivered to the detector via an optical fiber. The induced dispersion is compensated by the pair of diffractive gratings [21]. A correct signal was received in the range 0.1–1 THz, which was limited by the poor performance of the source below 0.1 THz. The exemplary signal gathered in the time domain, its Fourier transform (FT), and angular distribution are shown in Fig. 5.

Fig. 5
figure 5

a Typical temporal THz TDS signal without any sample, its b Fourier transform, and c angular distribution

Full size image

The sample was placed in the setup and illuminated by a Gaussian beam with a waist diameter of 30 mm (as measured for 0.3 THz). The waist and divergence of the beam obviously varied for different frequencies. The detector was moved along the circle with a diameter of 20 cm and the sample was located exactly in the center of rotation. The sample was tilted at the angle of 45° against the beam propagation vector, as seen in Fig. 4. The angular-frequency distribution of the THz signal with the reference flat slab in the sample holder is shown in Fig. 6.

Fig. 6
figure 6

Angular-frequency representation of the THz signal reflected from the uncoated (reference) slab

Full size image

The graph shows the angular shape of the Gaussian beam reflected by the sample, but it also exhibits periodical oscillations proving the presence of the Fabry-Perot effect. In order to underline this effect, the signal from all measured angles was averaged for a given frequency and plotted in Fig. 7.

Fig. 7
figure 7

Fabry-Perot oscillations seen in the averaged signal reflected from the uncoated sample

Full size image

The experimental measurements were then compared with the theoretical curve of F-P oscillations. In the theoretical model, the emitter and detector were assumed to have flat response and the material attenuation was not taken into account. The angle of incidence was 45° and the sample thickness was the same as in the experiment (i.e. 2 mm). Figure 8 shows the expected co-alignment of extremes of both curves, which proved that the observed oscillations are in fact the manifestation of the Fabry-Perot effect.

Fig. 8
figure 8

Fabry-Perot oscillations measured for uncoated PA-12 slab with incidence at 45°

Full size image

As the next step, two samples of PA-12 slabs were 3-D printed with the designed AR structure in order to prove the suppression of F-P oscillations for selected spectral regions. They were examined in the same experimental configuration, although this time both reflection and transmission were measured one by one by changing the angle of the detector, as depicted in Fig. 4. The measurements of the reflected field are shown in Fig. 9. Note that the zero angle denotes the direction at which the beam is reflected according to geometrical optics.

Fig. 9
figure 9

Experimentally measured amplitude of the THz field reflected from the PA-12 slab. a Without AR structure. b With one-sided AR. c With two-sided AR. The graphs are normalized to the same value

Full size image

The amplitude of the reflected field is significantly reduced due to the use of AR structures. Moreover, the reflected field is more confined near the zero angle. The reduction of reflections in spectral (frequency) domain is presented in Fig. 10, where each value is averaged by angles in the range from − 10° to + 10°.

Fig. 10
figure 10

Averaged amplitude of the reflected THz beam for different samples

Full size image

Apart from the overall reduction of the amplitude in the reflected beam, the characteristic F-P oscillations are highly suppressed, especially for f < 0.2 THz. Above 0.2 THz, the peak-to-peak amplitude of F-P oscillations dropped by a factor of 4.

The use of 3-D printed AR structures sustained the intensity of the beam transmitted in-line through the PA-12 slab, as expected. Figure 11 shows the amplitude averaged by angles in the range from − 10° to + 10°, where angle 0° denotes the direction of propagation of the THz beam from the emitter.

Fig. 11
figure 11

Amplitude of the THz beam transmitted in-line through different samples

Full size image

Below 0.17 THz, the transmission is increased, while above 0.17 THz, the AR layers have lowered the amount of THz energy reaching the detector. This is explained by the fact that the used AR structure partly works as a saw-tooth diffractive grating [22,23,24] for selected (shorter) wavelengths, as it was previously demonstrated e.g. for photo-induced gratings [25]. As a consequence, some of the transmitted energy falls at higher angles due to multi-order diffraction. In order to confirm this, a wide-angle TDS scan was executed on two-sided AR sample. The results are shown in Fig. 12.

Fig. 12
figure 12

Amplitude of the transmitted THz field for the wide-angle range, showing diffraction on the left side (for negative angles) in the first diffractive order (marked with a red rectangle) and in the second diffractive order (blue rectangle)

Full size image

The energy missing in the transmitted characteristics shown in Fig. 11 has been redirected by diffraction into different angles, depending on the relation between the wavelength and the physical periodicity of the printed AR pyramids. For this reason, the proposed AR structures are the most suitable for longer waves (i.e., 0.1–0.2 THz), which do not feel the periodicity of the AR, but rather interact with the sample as with a sub-wavelength structure having the effective refractive index. 3-D printed AR should perform well for even a lower terahertz range (e.g., 50 GHz), but those frequencies were out of the operating range of our emitter (see Fig. 5).

When the amplitude of the THz field transmitted through the sample is integrated over a wider angular range (− 60° to + 60°), the increase of the amplitude is evident and reaches 27 and 36% at 0.145 THz for one-sided AR and two-sided AR, respectively (see Fig. 13).

Fig. 13
figure 13

Amplitude of the transmitted THz field integrated over a wide angular range

Full size image

Table 1 shows the total amplitude of the transmitted and reflected THz signals integrated over the entire angular range. In the optimal range of frequency between 0.12 and 0.2 THz, the use of 3-D printed AR structure increased the transmitted amplitude by 14% (one-sided AR) and 23% (two-sided AR). The reflected amplitude was decreased by 26% (one-sided AR) and 77% (two-sided AR), which is a significant improvement taking into account the ease of design and fabrication.

Table 1 Total amplitude of the measured transmitted/reflected THz field shown as percentage of the amplitude from the emitter (numerical results given in parentheses)
Full size table

The presented quantitative and qualitative results are in a good agreement with numerical simulations performed using finite-difference time-domain (FDTD) method. Figure 14 compares the amplitude of transmitted, diffracted, and reflected THz fields for 0.1 THz (where the AR structure should work as an effective medium layer) and for 0.3 THz (where the diffraction is strongly visible). The integrated values from the simulations are also given in Table 1.

Fig. 14
figure 14

Numerical simulations of the interaction of the upward-propagating THz wavefront at 0.1 and 0.3 THz with the test sample without (“REF”) and with the one-sided and two-sided AR layers. The arrows show the direction of the impinging THz beam

Full size image

According to numerical results in Fig. 14, the use of AR layer has allowed the redirection of THz energy from the reflected beam to the transmitted/diffracted beam, leading to sustained transmission and strongly attenuated unwanted reflections, especially when the two-sided AR structure was used. These conclusions fully agree with the previously shown experimental outcome. Moreover, the matching values of experimental and numerical integrals in Table 1 prove that the assumed material absorption coefficient of α = 1 cm−1 [26] was correct. Based on the above results, the effective thickness of the uncoated sample was calculated to be 6.3 mm. It was longer than its physical width as the result of multiple reflections inside the PA-12 slab, which was also observed in simulations (see Fig. 15). The application of the two-sided AR layer has decreased the effective thickness of the sample from 6.3 to 2.0 mm.

Fig. 15
figure 15

Multiple passes of the radiation inside the sample, contributing to the increased absorbance

Full size image

5 Discussion and Conclusions

Additive manufacturing proves to be a promising technology for structuring of optical elements for the wavelengths in the millimeter range due to its ease of design and prototyping [26,27,28]. Especially for longer wavelengths around 0.1 THz, there is an attractive possibility of direct printing of sub-wavelength kinoform-like structures. Anti-reflection structures fabricated using this technology were tested in THz-TDS setup with goniometric angular measurements of both transmitted and reflected fields. AR layers successfully reduced the reflected energy and suppressed internal reflections leading to spurious Fabry-Perot interference. Moreover, they improved the total transmittance of the sample, but mostly for longer waves in the range where the diffraction of the THz beam on the AR structure was negligible. The experimental results were in good agreement with numerical simulations. The performance of the proposed AR layers may be improved in future work by optimizing the groove profile and periodicity of the pyramid design. Nevertheless, in the THz experiments, the most disturbing effect is the presence of unwanted multiple reflections, which can be strongly suppressed by the proposed solution.