Tracking Covid-19 cases and deaths in the United States: metrics of pandemic progression derived from a queueing framework

Abstract

We analyze the progression of COVID-19 in the United States over a nearly one-year period beginning March 1, 2020 with a novel metric motivated by queueing models, tracking partial-average day-of-event and cumulative probability distributions for events, where events are points in time when new cases and new deaths are reported. The partial average represents the average day of all events preceding a point of time, and is an indicator as to whether the pandemic is accelerating or decelerating in the context of the entire history of the pandemic. The measure supplements traditional metrics, and also enables direct comparisons of case and death histories on a common scale. We also compare methods for estimating actual infections and deaths to assess the timing and dynamics of the pandemic by location. Three example states are graphically compared as functions of date, as well as Hong Kong as an example that experienced a pronounced recent wave of the pandemic. In addition, statistics are compared for all 50 states. Over the period studied, average case day and average death day varied by two to five months among the 50 states, depending on data source, with the earliest averages in New York and surrounding states, as well as Louisiana.

Highlights

• Methodology motivated by queueing systems illustrates how the time distribution of disease events (cases and deaths) vary over time, by location.

• Geometric growth of daily cases and deaths results, in the limit, in a constant separation between the present day and the partial-average day of event. This phenomenon appeared in the early days of the pandemic, particularly in New York.

• Later in the pandemic, during a second or third wave, the partial average grew at rates exceeding one per day in the United States. Thus, the separation between the current day and the average day became smaller over time, offering an indicator of accelerating pandemic.

1 Introduction

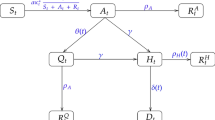
Throughout the COVID-19 pandemic, localities and countries have experienced oscillating periods during which rates of reported new cases and deaths have shifted from rapidly increasing to rapidly decreasing. Oscillations have challenged health care providers, as demands for nurses, doctors, medical equipment, hospital beds and other resources are constrained by available capacity, which can be insufficient to meet peak demands, which are many times the averages. To balance capacity with demand, providers have postponed surgical procedures or appointments, regulated inflow of new patients or augmented capacity with temporary facilities, repurposed spaces or supplemental staffing (e.g., traveling nurses). These strategies are among a large array of interventions available to public health authorities and health systems for optimizing patient flow in the presence of a novel and highly transmissible virus. Figure 1 classifies potential interventions from the combined perspective of disease progression and health care delivery.

Fig. 1

Interventions to Improve Patient Flow for Human Transmissible Disease

Interventions for managing patient flow anticipate future cases and hospitalizations, not knowing whether rates of new infections will match expectations. Small changes in transmissibility of disease, perhaps due to changes in collective human behavior, can result in highly inaccurate forecasts. While models for disease transmission might predict new cases well if the underlying conditions governing transmission are static, they can be far from accurate when conditions change. For these reasons, it is important to gain an empirical understanding of the variability in new infections and other disease metrics.

In this paper, we investigate patterns of COVID-19’s spread in the United States by examining the time distribution of events, where an event is defined by a point in time when either a new case or new death is attributed to COVID-19. We focus on the cumulative distribution of events within time-periods along with the average time of events occurring within time-periods. Both measures are traditional metrics used for queueing systems. In a similar manner, they can be used to understand relationships between sequential disease events (cases then deaths) as well as variations in the distributions of events.

From a queueing perspective, an infection (reported as a case) represents a system arrival. A death or recovery represents a departure. Both types of events are temporal point processes. Unlike many queueing systems, there is no expectation that arrival events are mutually independent, as a consequence of four types of dependencies. First, a new infection results from exposure to a person who was previously infected, so new “arrivals” are precipitated by prior arrivals. Second, exposure is a consequence of collective human behavior, which is influenced by public health policies (such as hygiene or distancing measures) and community norms (e.g., willingness to follow standards that reduce exposure). Third, as virus variants emerge, disease transmissibility may change, affecting rates of new infections. Last, as individuals acquire immunity, either through infection or programs for vaccination, fewer people are susceptible to new exposure and infection. These four types of dependencies can alter patterns of disease in unpredictable ways, shifting from a phase when rates of new infections are rapidly increasing to a phase when rates of new infections are rapidly decreasing (or vice versa).

Beyond understanding variation, we also seek to understand data coherence, specifically whether cases and reported deaths are counted consistently over time. We compare three data sources: the Centers for Disease Control’s (CDC) data on reported cases and deaths as was as “Covidestim” and “Covid-19 Projections,” which have used inference methods to estimate actual infections and deaths. Our aim is to illustrate and measure actual variations, offering insights that could inform capacity planning.

Our research provides normalized metrics as to when the disease accelerated and decelerated by location and how the disease patterns varied among the 50 United States. As the novel Coronavirus disease-19 (COVID-19) pandemic progressed across the United States in 2020 and early 2021, the rates of cases and deaths varied by week and month among states. While at the national level the United States faced three major case waves (Spring 2020, Summer 2020, and Winter 2020/21) during our period of study, the time distribution of cases and deaths has varied by location. Very early in the pandemic, large urban areas, especially in the northeast, had the highest rates of cases and deaths. New York City was the pandemic’s epicenter, registering 203,000 laboratory-confirmed cases in the first three months of the pandemic [19]. However, by July 2020, southern states, such as Florida, Texas, and Arizona, became hot spots for the pandemic. By late summer and early fall, Midwestern states, such as North Dakota, South Dakota, and Iowa, surged in cases and deaths [9]. Rural areas were hardest hit during this period. November through January represented a national surge in cases, when many states recorded new highs in cases. States with lower case rates in the summer, like New York and New Jersey, had surges again. In December of 2020, 21 states registered at least 2,000 new cases per 100,000 residents per month, and 26 states had rates between 1,000 and 2,000 new cases per 100,000 residents per month [5]. By February, case rates started dropping across the United States.

Our metrics provide a novel assessment of the progression of the disease, offering a supplemental way to examine the current state of the disease in the context of the entire history of cases and deaths. The intent is to offer indicators of whether data on cases and deaths reflect a historical phenomenon (many days or years in the past, on average), or whether the pandemic is more current (cases and deaths are on average more recent, or are becoming more recent).

In the following section, we review prior research examining patterns of COVID-19 in the United States. We next introduce our methodology for developing metrics for tracking disease-related events and illustrate these metrics for an example of geometric growth and decay. Then we present results, including graphs representing example states and a comparison of statistics for all 50 states. We end with conclusions and discussion.

2 Literature review

As the novel coronavirus spread worldwide, cases, hospitalizations and deaths have been studied with epidemiological models, characterizing the COVID-19 epidemic, forecasting transmission, and evaluating pharmaceutical and non-pharmaceutical intervention. Mathematical methods, such as compartmental models, statistical models, general machine learning models, and agent-based models have been applied to simulate, characterize, and forecast COVID-19 [2, 3, 6, 14, 21].

Early mathematical models of COVID-19 updated previous disease models to consider the unique characteristic of COVID-19 [18], including updating older SIR models to consider hospitalized and undetected infections [10, 16, 18]. Other research focused on risk factors and epidemiological characteristics of COVID-19 patients, such as fevers and coughing [13, 17, 22]. Early research focused on Wuhan, prior to when the disease spread to other countries. Later research focused on how the outbreak dynamics had differed in countries such as China and the United States [12]. This type of research started analyzing localities because of differing transmission rates, which may be related to human behavior, living conditions and environmental factors. Furthermore, epidemiological research started looking at transmission rates in different settings (i.e., homes and work) in other countries.

To inform intervention efforts, state and local health departments have used various indicators to identify the changes in the number of cases, hospitalization, and deaths. For example, the Kentucky Department for Public Health (KDPH) adopted composite syndromic surveillance data: number of new cases, number of COVID-19 associated deaths, health care capacity data, and contact tracing capacity as five indicators to assess the state-level COVID-19 status [20]. From empirical data, they scored each of the five indicators using a 3-point scale (3= excellent, 2 =moderate, 1 = poor), and then combined the five scores with equal weights to a composite state-level COVID-19 status by a 5-point rating system. They found that during May 19 – July 15, 2020, the Kentucky composite COVID-19 status worsened. Similarly, King County in Washington state was among the first to publish a key indicators dashboard to provide an overview of COVID-19 progression in: disease activity, testing and healthcare system status [11]. They calculated the 7-day average for cases per capita, 7-day average hospitalization per capita, 7-day average deaths per capita, effective reproduction number, and hospital bed occupancy. The performance in each area could be compared against targets. These indicators provided a plain language assessment to facilitate reopening decisions.

In addition, health care indicators can help compare the healthcare outcomes across different groups of people. For example, cumulative death counts are associated with demographic characteristics. Heuveline and Tzen proposed three measures – the crude death rate, the age-standardized death rate, and life expectancy at birth – to compare status over time [8]. They disaggregate the population into smaller administrative units with respect to age and sex to provide more meaningful comparisons.

During the pandemic, it has been apparent that data and predictions influence policy decisions aimed at lessening the impact of COVID-19, yet suffer from significant uncertainty. In this environment, it is difficult to develop the most effective interventions, and instill public confidence that the most effective interventions have been selected [1, 15].

Our research focuses on a novel way to track data on cases and deaths. We focus on the time distribution of cases and deaths as a standardized indicator for the time-varying dynamic of the pandemic, showing when it is accelerating or decelerating in the United States on a state level. We calculate and compare partial averages by day to quantify the progression of the disease. We focus on state-level data to model how the progression of the disease has affected each state of the country at different times. Finally, we assess three data sources to understand how different estimation methods (relative to official counts of reported cases and deaths) affect how the pandemic appears to have developed in each state.

3 Methodology

Our research analyzes the time distribution of reported (and estimated) cases and deaths attributed to COVID-19 in the United States, beginning on March 1 of 2020. We focus on the time distributions of reported events, as indicators of the pandemic’s progression by location. In this section we develop a methodology for analyzing event statistics, focusing on partial averages, as a function of date, along with the cumulative distribution of events in the study period. An idealized geometric progression is used to illustrate properties of time partial averages. Understanding the properties of the idealized model will help to understand empirical results, which is the focus of Section 4.

3.1 Computing partial averages by day

We consider a process where events are tracked over time by counting the number occurring on each day. Our focus is on cases (and estimated infections) and deaths, but the concepts generalize to any process where events(i.e. points) are counted by time increment. We seek to track partial averages, representing the average day of events occurring on day t or earlier. Let:

A(t) = average event day, for events occurring on day t or earlier.

Day 1 $(t=1)$ represents the day of the first recorded event.

By definition, A(1) must equal 1. A(t) is a non-decreasing function, with these properties:

$A(t+1) > A(t)$ if new events occur on day $t+1$

$A(t+1) = A(t)$ if no new events occur on day $t+1$

Let:

T = day of last recorded event

P(t) = cumulative relative frequency of events, day t or earlier

By definition, P(T) = 1, as all events must occur before day T. Let:

p(i) = relative frequency of events for day i

For example, if 5 events occurred on days 1 and 2, then $A(2) = 1.5$, the average of the two days. If 5 more events occurred on day 3, A(t) would rise to 2 on day 3, the average of the 3 days. However, if no event occurred on day 3, A(t) would remain at 1.5. Then:

$$\begin{aligned} P\left( t\right) =\sum \limits _{i=1}^{t}p\left( i\right) \end{aligned}$$

(1)

For example, if $T = 3$ and five events occur on each day, $p(1) = p(2) = p(3) = \frac{1}{3}$, and $P(1) =\frac{1}{3}, P(2) = \frac{2}{3}$, and $P(3) = 1$.

$$\begin{aligned} A\left( t\right) =\sum \limits _{i=1}^{t}{i\bullet p\left( i\right) /P\left( t\right) } \end{aligned}$$

(2)

As a simple example, if the event frequency is identical on all days, $A(1) = 1$, and then increases by .5 each day thereafter $(A(2)=1.5, A(3)=2,\ldots )$. If frequencies are increasing, then A(t) will increase at a faster rate, and if event frequencies are decreasing, the rate of growth will be slower.

$A(t+1)$ can be computed as a weighted average, as follows:

$$\begin{aligned} A\left( t+1\right) =&A\left( t\right) \bullet \left[ P\left( t\right) /P\left( t+1\right) \right] \nonumber \\&+\left( t+1\right) \bullet \left[ p\left( t+1\right) /P\left( t+1\right) \right] \end{aligned}$$

(3)

As a simple example, suppose that 5 cases (i.e., events) occur on day 1, 10 on day 2, 15 on day 3 and 10 on day 4, with $T=4$ and $P(4)=1$. Then $p(1) = 5/40$, $p(2) = 10/40$ and so on; $P(1) = 5/40$, $P(2) = 15/40$ and so on. By definition, $A(1) = 1$. A(2) is then a weighted average of the 5 events on day 1 and 10 events on day 2, or 1.67. Equivalently, A(2) can be calculated recursively from Eq. 3: $A(1)*P(1)/P(2) + (2)*p(2)/P(2)$, or $1*(5/40)/(15/40) + 2*(10/40)/(15/40)$, which also produces the result 1.67. Repeating Eq. 3, $A(3) = 2.33$ and $A(4) = 2.75$. The rate of increase in A(t) declines on day 4 because the number of cases (i.e., events) declines on day 4.

Let $\triangle (t+1)$ represent the change in average event time from day t to day t+1:

$$\begin{aligned} \triangle (t+1)=A(t+1)\;-\;A(t) \end{aligned}$$

(4)

$\triangle (t+1)$ can be derived algebraically from Eq. 3, resulting in:

$$\begin{aligned} \triangle (t+1)=[p(t+1)/P(t+1)]\bullet [(t+1)-A(t)]\end{aligned}$$

(5)

Equation 5 offers insight into how rapidly A(t) changes as a consequence of $p(t+1)$, rising fastest in time periods when the frequency of an event exceeds the rate of events in the preceding days, such as when events are occurring at an accelerating rate. Another insight is that A(t) can grow particularly fast in a second or later wave of a pandemic. After an initial wave, A(t) may remain stable for a period of time, as $p(t+1)$ is small. If a pandemic re-emerges, then A(t) may grow rapidly, both because $p(t+1)$ is large and because $t+1$ is now much greater than A(t) (owing to the prior lull when A(t) was increasingly slowly).

3.2 Geometric growth and decay example

To understand patterns in empirical data from COVID-19, we first explore the characteristics of the idealized scenarios of geometric growth and decay, characterized by the function:

$$\begin{aligned} n\left( t+1\right) =n\left( t\right) \bullet \alpha =n\left( 1\right) \bullet \alpha ^{t} \end{aligned}$$

(6)

where

$n\left( t\right)$ = number of events occurring in day t

$\alpha$ = rate of growth (or decay) in events .

Geometric growth occurs when $\alpha$ is greater than 1, geometric decay when $\alpha$ is less than 1, and events occur at a constant rate when $\alpha$ equals 1. Let:

N(t) = cumulative events from day 1 to day t

N(t) is a counting process. Then:

$$\begin{aligned} N\left( t\right) =\sum _{i=0}^{t-1}{n\left( 1\right) \bullet }\alpha ^{i} \end{aligned}$$

(7)

As a geometric progression, N(t) can be expressed:

$$\begin{aligned} N(t)=\left\{ \begin{array}{ll} &{} \left[ (1-\alpha ^{t})/\left( 1-\alpha \right) \right] \bullet n\left( 1\right) ,\;\;\alpha \ne 1\\ &{} t\bullet n\left( 1\right) ,\;\;\alpha =1 \end{array}\right. \end{aligned}$$

(8)

As defined in Eq. 4, $\triangle (t+1)$ is the change in the average event day from day t to day $t+1$. Substituting $n(t+1)/N(t+1)$ from above for the ratio $p(t+1)/P(t+1)$:

$$\begin{aligned} \triangle (t+1)={}&\{\alpha ^{t}/[(1-\alpha ^{t+1})/(1-\alpha )]\}\bullet \{t+1-A(t)\},\;\; \alpha \ne 1 \end{aligned}$$

(9)

In the special case where $\alpha = 1$ (constant frequencies), $\triangle (t+1) = .5$ for all values of t, and A(t) is simply $(t+1)/2$. Consider two other examples. If $\alpha = .5$, a pattern of geometric decay, $\triangle (t+1)$ is a declining function: .333,.238,.161 for $t = 1,2,3,\ldots$, with declining values of p(i) and A(t) approaching a limiting value of 2. If $\alpha = 2$, a pattern of geometric growth, $\triangle (t+1)$ is an increasing function: .667,.762,.838 for $t = 1,2,3,\ldots$, with increasing values of p(i) and A(t), approaching a constant growth rate of 1.

More generally, for the case where $\alpha > 1$ (geometric growth), $\triangle (t+1)$ is always an increasing function, approaching the limit:

$$\begin{aligned} \begin{array}{ll} {\lim }_{t\rightarrow \infty }\triangle (t+1){}&=[(\alpha -1)/\alpha ]\bullet \{t+1-A(t)\}=1,\;\;\alpha >1 \end{array} \end{aligned}$$

(10)

And further,

$$\begin{aligned} {\lim }_{t\rightarrow \infty }A(t)=t-1/(\alpha -1),\;\;\alpha >1 \end{aligned}$$

(11)

It should be noted that algebraic substitution of the limiting equation for A(t) from Eq. 11 in Eq. 10 yields an equality. In the special case where $\alpha < 1$ (geometric decay), $\triangle (t+1)$ is a decreasing function, approaching the limit:

$$\begin{aligned} {\lim }_{t\rightarrow \infty }\triangle (t+1)=0,\;\;\alpha <1 \end{aligned}$$

(12)

And, further,

$$\begin{aligned} {\lim }_{t\rightarrow \infty }A\left( t\right) =1/\left( 1-\alpha \right) ,\;\;\alpha <1 \end{aligned}$$

(13)

The properties of A(t) are illustrated in Fig. 2 for example rates of growth (10%, $\alpha = 1.1$; 5%, $\alpha = 1.05$) and decay (5%, $\alpha =.95$), as well as constant (0%, $\alpha = 1.0$). For instance, for 10% growth, A(t) approaches $t - 10$ (equaling $t - 1/(1-\alpha )$) with near-constant growth rate of $\triangle (t+1) = 1$ apparent after day 90; for 5% decay, A(t) approaches 20, equaling $1/(1-\alpha )$.

Fig. 2

Average Day of Event as Function of Day (geometric growth or decay, by % daily change)

For another metric, we introduce:

H(t) = days elapsed since average event on day $t = t-A(t)$.

Figure 3 illustrates the limiting properties of H(t), which approaches the constant $1/(1 - \alpha )$ under geometric growth; approaches $t-1/(1-\alpha )$ under geometric decay; and equals t/2 when $\alpha = 1$. Last, Figure 4 plots $H(t+1) - H(t)$, illustrating again that for geometric growth, H(t) approaches a limiting value as t becomes large, yet approaches a constant growth rate of 1 for geometric decay.

Fig. 3

Days Since Event as Function of Day (geometric growth or decay, by % daily change)

Fig. 4

Daily Change in Average Days Since Event as Function of Day (geometric growth or decay, by % daily change)

As we examine empirical data in individual states in Section 4, we will look for signs of geometric growth (when the pandemic is accelerating) or decay (when the pandemic is waning) through our examination of A(t) for cases and deaths. As mentioned, $\triangle (t+1)$ never exceeds one for the idealized geometric model. As will be seen on data, $\triangle (t+1)$ can exceed one when events occur in multiple waves, as has been the case for COVID-19.

3.3 Source data and indicators

We compared data from three sources: CDC reported data, Covidestim estimated data, and COVID-19 Projections estimated data. Estimated data attempt to correct for errors in reporting, which might, for example, include infections that were never detected through testing.

CDC reported data includes two metrics for both recorded cases and deaths: confirmed case or death and probable case or death [14].The CDC defines a confirmed case or death as met by confirmed laboratory evidence for COVID-19. Furthermore, the CDC defines a probable case or death as meeting one of three standards [13]:

• Clinical criteria and epidemiological evidence with no confirmed laboratory testing

• Laboratory evidence and either clinical criteria or epidemiological evidence

• Vital records with no confirmatory laboratory testing

We used the total combined count of confirmed and probable cases and deaths. The CDC also further explains how the reported data can fluctuate [13], due to:

• Jurisdictions reclassifying probable cases

• Counts being revised as records are finalized

• Jurisdictions having different reporting time intervals and methodologies for reporting cases and deaths

• Delays in reporting and testing.

We compared metrics for CDC data to two estimated data sources: Covidestim and COVID-19 Projections. Covidestim is an experimental methodology using Bayesian evidence synthesis to adjust reported data, accounting for asymptomatic infections, undercounting due to lack of availability of testing, and delays in case and death counts [4]. The model was run every 28 days, given the lag time for observed data, and is parameterized by four health states: asymptomatic, symptomatic, severe, and death [4].

COVID-19 Projections is an experimental “nowcasting” model that aims to standardize the test positivity and estimate for the true incidence of COVID-19. The model adjusts the test positivity by taking the average ratio for each date and applying this ratio to states that report “unique people” [7]. Next, the model estimates the prevalence ratio by using the positivity rate and date to estimate true infections. Finally, the model estimates the number of infections by parametrizing the prevalence ratio, positivity rate, and confirmed cases using a 7-day moving average. For our purposes, we will use COVID-19 Projections estimated infections and total deaths.

Our analysis is based on the period March 1, 2020 through February 21, 2021, with the end date matching the end date of COVID-19 Projections’ estimation of infections. Data were downloaded on these dates: Covidestim, June 25, 2021; COVID-19 Projections, June 26, 2021; CDC, June 25, 2021. For our analysis we utilized data for total numbers of cases and deaths in each state by date. The results, which represent time-of-event distributions, are invariant as to whether they are based on total numbers or per capita event numbers (such as cases and deaths per 100,000 people).

4 Results

We examined case and death statistics/estimates for COVID-19 for all 50 of the United States for the three data sources CDC, Covidestim and COVID-19 Projections. For each state and data source, we calculated A(t) and P(t) for deaths and cases. We also compared statistics as follows. Let:

$A_d(t)$ = average death day for events occurring on day t or earlier

$A_c(t)$ = average case day for events occurring on day t or earlier .

We then computed the difference between average death day and average case day:

$L(t) = A_d(t)-A_c(t)$.

Though for any individual, deaths must follow initial infection, we will see that L(t) is not necessarily positive. A rapidly declining value of L(t) can be a sign of an impending pandemic wave, because the average day of case rises prior to the associated average day of death. L(t) might also turn negative if there is a change that increases reporting of cases, or perhaps if survival rates after exposure improve.

We also calculated the ratios:

$$\begin{aligned} R_d(t)= & {} A_d(t)/t\\ R_c(t)= & {} A_c(t)/t \end{aligned}$$

These ratios are naturally close to one at the onset of a pandemic (i.e., average day of event is similar to the current day, and identical on day one). They remain close to (but smaller than) 1 if cases and/or deaths grow geometrically, approaching 1 in the limit (Eq. 11. for the limiting value of A(t), divided by t, approaches 1 for large values of t). For geometric decay, the ratios approach 0 (Eq. 13. divided by t approaches 0 for large values of t because A(t) approaches a constant). For constant frequency of events ($\alpha = 1$), the ratio approaches .5, with the average day of event half of the current day. In this manner, they are indicators of the progression of a pandemic.

4.1 Disease patterns in example states

For illustration, graphs are presented here for California. Figure 5,6,7 shows results for CDC, COVID-19 Projections and Covidestim data respectively (Figures S1, S2, S3 provide results for New York and Figures S4, S5, S6 show results for Minnesota). In each example, plots are provided for A(t), L(t), and R(t) for cases and death, which are invariant to T, the length of the study period. The cumulative probability distributions of cases and deaths are also provided, which do depend on T because the graph is scaled to equal exactly 1 at the end of the study period.

Examining the slopes of $A_d(t)$ and $A_c(t)$, geometric growth can be seen in the first 50 days of the pandemic, where these functions increase at an approximate rate of one per day. Between day 50 and 250, $A_d(t)$ and $A_c(t)$ increase at slower rates, as reflected in dropping values of $R_d(t)$ and $R_c(t)$, indicators that the pandemic waned during that time period. That pattern reversed between day 250 and 300, when $A_d(t)$ and $A_c(t)$ increased at rates exceeding one per day, as a second wave of the pandemic began to overwhelm the magnitude of the first wave.

One would expect that cumulative probability distributions for deaths and cases would follow similar patterns, with deaths lagging cases, unless there has been notable changes in survival rates over time. Yet plots of L(t) fell well below zero, dropping to almost -40 around day 300, before rising at the end of the study period. Other than possible improvement in survival, there are two explanations. First, cases were relatively under-reported at the start of the pandemic, thus creating an upward bias in the dates of reported cases. Second, in the later wave of the pandemic, cases appeared prior to deaths, thus creating a temporary dip in the L(t) indicator.

Comparing the three data sources, measures of deaths are similar, but measures of cases differ significantly. Under COVID-19 projections, cases are distributed earlier in the pandemic, more closely following the patterns of deaths, which were perhaps a more accurate indicator of actual infections.

Fig. 5

Average Day of Event in California using CDC’s Data

Fig. 6

Average Day of Event in California using COVID-19 Projection’s Data

Fig. 7

Average Day of Event in California using Covidestim’s Data

4.2 Comparison of statistics for all 50 states

We now examine comparative statistics for the 50 states. For each state, we calculated the average case day and average death day, as of 2/21/2021, for all three data sources. The distribution of these statistics was then plotted as cumulative distributions in Figs. 8 and 9. As shown in Fig. 8, average case day, computed from Covidestim, varies from 229 (Louisiana) to 280 (Wyoming), with an average (of the averages) of 253 (Table 1). For contrast, case averages from COVID-19 Projections range from 139 (New Jersey) to 283 (Wyoming) with an average (of the averages) of 227. Thus, the latter estimates show cases occurring much earlier in states that experience the most severe outbreaks in the March/April 2020 timeframe, yet only 26 days earlier on average among all states. The distributions of average death day are similar to COVID-19 Projections’ case day distribution, with averages ranging from about 133 to 283.

Table 1 Statistics for Average Case and Death Day by State

Figure 10 shows how L(t) varied from month to month. For each month and each state, we counted the number of days that L(t) was positive (i.e., average death day is later than average case day) and then computed an average for this statistic among the states. These results are shown for the three data sources, expressed as the percentage of days within the month. The percentages peaked in April and May, toward the end of the first wave of the pandemic. They dropped to a minimum toward the peak of the December wave, as cases appeared prior to associated deaths. However, even as the pandemic waned in February 2021, the average case day tended to be later than the average death day (though less so with COVID-19 Projections).

Figures 11, 12, 13 provide a final graphical comparison among states, which are color-coded as to the average case days for CDC and COVID-19 Projections data, and average death day for CDC data. Notably, CDC case data suggest a much narrower distribution for the time distribution of the pandemic than either CDC death data or COVID-19 Projections case data, for which the pandemic is shown to occur much earlier in New York and surrounding states, as well as in Louisiana. These distinctions are critical to capacity planning, as the needs for supplemental healthcare resources and public health intervention occur much earlier in the pandemic than CDC data would suggest, likely because infections were much less likely to become reported cases early in the pandemic.

Fig. 8

Cumulative Probability Distribution for Average Day of Case Among States

Fig. 9

Cumulative Probability Distribution for Average Day of Death Among States

Fig. 10

Average % of Days that Average Death Day is Greater than Average Case Day (March 2020 to February 21, 2021)

Fig. 11

Average Case Day on 2021-02-21 (CDC)

Fig. 12

Average Death Day on 2021-02-21 (CDC)

Fig. 13

Average Case Day on 2021-02-21 (COVID-19 Projections)

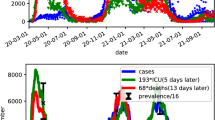
4.3 Disease patterns in hong kong and metric comparison

We conclude with a comparison example from a different world region to illustrate features of the metrics. By reported data, Hong Kong did not experience large numbers of cases and deaths until early 2022. In the cumulative probability graph in Fig. 14, cases and deaths were imperceptible in 2020 and 2021. Nevertheless, earlier waves occurred in the summer of 2020 and winter of 2020/21, as revealed in rises in average day of case and death, also in Fig. 14. Moreover, the value of tracking average days can be seen by noting that the metric noticeably increases early in the winter 2022 wave, much earlier than is perceptible for the cumulative graph. Average day also peaks earlier, providing an early sign of when the wave is now ebbing. It might also be noted that by tracking the difference between average day and death, a clear sign is provided as to when the wave changes direction from growth to decline, in mid-February, which is harder to detect in the cumulative graph.

Finally, the conventional metrics of weekly cases and deaths per 100,000 people are plotted within Fig. 14 at the bottom. Unlike the metrics developed in this paper, the conventional metric shows the magnitude of the pandemic as a function of date, quantified by recorded events per week. However, it is harder to discern dynamic changes, as to when the pandemic surged and dissipated. For instance, the plot of average death day minus average case day offers a clear early signal of an impending surge, with a pronounced decline in January, 2022, well before the large rise in cases per week shown in the bottom graph. The conventional metric of cases or deaths per 100,000 people, while helpful in showing relative magnitudes by date, is nevertheless less effective in visualizing their relative dynamics, as deaths are only a small fraction of cases. Changes in the relative timing of cases and deaths are more apparent in the metrics developed in this paper. These points do not diminish the importance of tracking cases and death per 100,000 people, but do illustrate why other metrics can be helpful.

Fig. 14

Average Day of Event in Hong Kong using Our World In Data as of 05-10-2022

5 Discussion and conclusions

We have developed and applied a methodology motivated by queueing systems to illustrate how the time distribution of disease events (cases and deaths) vary over time, by location. We see how geometric growth of daily cases and deaths result, in the limit, in a constant separation between the present day and the average event day, and we see how this phenomenon appeared in the early days of the pandemic, particularly in New York. When the partial average grows at the rate of one per day, the average date of a case or death has not moved further into history.

We found that later in the pandemic, during a second or third wave, the partial average grew at rates exceeding one per day. Thus, the separation between the current day and the average day became smaller, signs that the pandemic has switched from a state of improvement to a state of growing rates of cases. Thus, the average date is moving closer to the present, placing the locality closer to the center of the pandemic (as reflected in time average).

We also observed that the time distribution varied by several months among the 50 states, as the pandemic accelerated and decelerated at different times. Last, we observed that the average day of deaths preceded the average day of cases much of the time, particularly during the December 2020 to January 2021 period. Last, examining Hong Kong for comparison, we saw how the metrics developed in this paper are helpful in visualizing the progression of the pandemic through various waves.

This paper has provided a framework, derived from queue models, through which the time distribution of cases and deaths can be compared by location and data source as well as compared to each other. These representations supplement conventional measures to provide insights into both the accuracy of underlying data and the actual state of disease by locality. The analyses might be used to align health care capacity with historical patient demands or to implement public health interventions that reduce disease transmission, so that healthcare capacity is not exceeded. They are intended to supplement conventional metrics to visualize changes in the pandemic that would otherwise be harder to detect.