Gravity Anomalies of Arbitrary 3D Polyhedral Bodies with Horizontal and Vertical Mass Contrasts

Abstract

During the last 15 years, more attention has been paid to derive analytic formulae for the gravitational potential and field of polyhedral mass bodies with complicated polynomial density contrasts, because such formulae can be more suitable to approximate the true mass density variations of the earth (e.g., sedimentary basins and bedrock topography) than methods that use finer volume discretization and constant density contrasts. In this study, we derive analytic formulae for gravity anomalies of arbitrary polyhedral bodies with complicated polynomial density contrasts in 3D space. The anomalous mass density is allowed to vary in both horizontal and vertical directions in a polynomial form of $\lambda =ax^m+by^n+cz^t$, where m, n, t are nonnegative integers and a, b, c are coefficients of mass density. First, the singular volume integrals of the gravity anomalies are transformed to regular or weakly singular surface integrals over each polygon of the polyhedral body. Then, in terms of the derived singularity-free analytic formulae of these surface integrals, singularity-free analytic formulae for gravity anomalies of arbitrary polyhedral bodies with horizontal and vertical polynomial density contrasts are obtained. For an arbitrary polyhedron, we successfully derived analytic formulae of the gravity potential and the gravity field in the case of $m\le 1$, $n\le 1$, $t\le 1$, and an analytic formula of the gravity potential in the case of $m=n=t=2$. For a rectangular prism, we derive an analytic formula of the gravity potential for $m\le 3$, $n\le 3$ and $t\le 3$ and closed forms of the gravity field are presented for $m\le 1$, $n\le 1$ and $t\le 4$. Besides generalizing previously published closed-form solutions for cases of constant and linear mass density contrasts to higher polynomial order, to our best knowledge, this is the first time that closed-form solutions are presented for the gravitational potential of a general polyhedral body with quadratic density contrast in all spatial directions and for the vertical gravitational field of a prismatic body with quartic density contrast along the vertical direction. To verify our new analytic formulae, a prismatic model with depth-dependent polynomial density contrast and a polyhedral body in the form of a triangular prism with constant contrast are tested. Excellent agreements between results of published analytic formulae and our results are achieved. Our new analytic formulae are useful tools to compute gravity anomalies of complicated mass density contrasts in the earth, when the observation sites are close to the surface or within mass bodies.

Appendix: Closed Forms for Edge Integrals

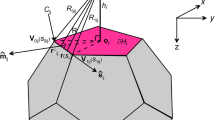
We begin to derive the closed forms for edge integrals $B_{j}^{q+2}$ and ${\mathbf {B}}_{j}^{q+2}$. In Fig. 1, given the edge $C_{j} \in \partial H_{i}$ with two ordered vertices $v_{0}$ and $v_{1}$, the unit tangential vector of edge $C_{j}$ is $\hat{\mathbf {e}}_{j} = (\mathbf {v}_{1} - \mathbf {v}_{0})/|\mathbf {v}_{1} - \mathbf {v}_{0}|$. Edge $C_{j}$ is parametrized by a single variable s, $s=({\mathbf {r}}-{\mathbf {o}})\cdot \hat{\mathbf {e}}_{j}$. Furthermore, $R=|{\mathbf {r}}^{\prime } -{\mathbf {r}}|=(h_{i}^2+m_{j}^2+s^2)^{1/2}$, $({\mathbf {r}}-{\mathbf {o}})=\mathbf {\rho }\hat{\varvec{\rho }}$, and $\hat{\varvec{\rho }}$ is a unit vector pointing from point ${\mathbf {o}}$ to point ${\mathbf {r}}$. The solid angle in Eqs. (33) and (34) is calculated as (Wilton et al. 1984)

$$\begin{aligned} \beta ({\mathbf {o}}) = \sum _{j=1}^{M} \beta ({\mathbf {o}})_{j} = \sum _{j=1}^{M} \hat{\mathbf {m}}_{j}\cdot \hat{\varvec{\rho }}_{j}^{\perp }\left( \arctan \frac{s_{1}}{|m_{j}|} -\arctan \frac{s_{0}}{|m_{j}|}\right) . \end{aligned}$$

(48)

Here $\hat{\mathbf {\rho }_{j}}^{\perp }$ is the unit vector from point ${\mathbf {o}}$ to point ${\mathbf {r}}_{\perp }$. At point ${\mathbf {r}}_{\perp }$, $s=0$. When point ${\mathbf {o}}$ is inside the polygon $\partial H_{i}$, $\beta ({\mathbf {o}})=2\pi$; $\beta ({\mathbf {o}})=\pi$ when point ${\mathbf {o}}$ is on an edge of polygon $\partial H_{i}$; $\beta ({\mathbf {o}})=\varTheta$ when point ${\mathbf {o}}$ is at a corner of polygon $\partial H_{i}$ with the corner angle $\varTheta$; $\beta ({\mathbf {o}})=0$ when point ${\mathbf {o}}$ is outside of polygon $\partial H_{i}$.

Using the integral tables from Gradshteyn and Ryzhik (1994, equation (2.260.2)), we get

$$\begin{aligned} {\mathbf {B}}_{j}^{q+2}=\hat{\mathbf {m}_{j}} \int _{C_{j}}R^{q+2}\hbox {d}l&= \hat{\mathbf {m}_{j}} \int _{s_{0}}^{s_{1}}\left( \sqrt{h_{i}^2+m_{j}^2+s^2}\right) ^{q+2}\hbox {d}s \nonumber \\&= \frac{\hat{\mathbf {m}_{j}}}{q+3} s R^{q+2} \mid _{s_{0}}^{s_{1}} + \hat{\mathbf {m}_{j}}\frac{q+2}{q+3} (h_{i}^2+m_{j}^2) \int _{C_{j}} R^{q}\hbox {d}l, \end{aligned}$$

(49)

where $s_{0}$ and $s_{1}$ are the parametrized coordinates of the vertices $\mathbf {v}_{0}$ and $\mathbf {v}_{1}$, respectively. To compute the gravity field (with $q=-1,1$), we only need to calculate terms $\int _{C_{j}} R\hbox {d}l$ and $\int _{C_{j}} R^3\hbox {d}l$ which are regular even if the observation site ${\mathbf {r}}^{\prime }$ is located on an edge $C_{j}$. The initial value for the recursive algorithm given by Eq. (49) is

$$\begin{aligned} \int _{C_{j}} R \hbox {d}l&= \frac{1}{2}\{(h_{i}^2+m_{j}^2) \ln \frac{s_{1}+R_{1}}{s_{0}+R_{0}} + s_{1}R_{1} - s_{0} R_{0} \}, \end{aligned}$$

(50)

where $R_{1}$ and $R_{0}$ are the distances from the point ${\mathbf {r}}^{\prime }$ to the vertices $\mathbf {v}_{0}$ and $\mathbf {v}_{1}$, respectively. When the observation site ${\mathbf {r}}^{\prime }$ is located on an edge $C_{j}$, we simply set $(h_{i}^2+m_{j}^2)=0$ which eliminates the possible logarithmic singularity in expression (50).

Now, we deal with term $B_{j}^{q+2}=\int _{C_{j}} \frac{R^{q+2}}{\rho ^{2}} \hbox {d}l$ ($q=-1,1$) in Eq. (34). When $q=-1$, we have,

$$\begin{aligned} B_{j}^{1}= m_{j} \int _{C_{j}} \frac{R}{\rho ^{2}} \hbox {d}l&= m_{j} \int _{s_{0}}^{s_{1}} \frac{\sqrt{h_{i}^2+m_{j}^2+s^2}}{m_{j}^2+s^2} \hbox {d}s \nonumber \\&= m_{j} \left( \frac{|h_{i}| \arctan (\frac{|h_{i}| s }{m_{j} R}) }{m_{j}}+\ln (s+R) \right) |_{s_{0}}^{s_{1}} \nonumber \\&= |h_{i}| \left( \arctan \frac{|h_{i}| s_{1}}{m_{j} R_{1}} - \arctan \frac{|h_{i}| s_{0}}{m_{j} R_{0}}\right) + m_{j} \ln \frac{s_{1}+R_{1}}{s_{0}+R_{0}}. \end{aligned}$$

(51)

When $q=1$, we have,

$$\begin{aligned} B_{j}^{3}= m_{j} \int _{C_{j}} \frac{R^{3}}{\rho ^{2}} \hbox {d}l&= m_{j} \int _{s_{0}}^{s_{1}} \frac{(\sqrt{h_{i}^2+m_{j}^2+s^2})^{3}}{m_{j}^2+s^2} \hbox {d}s \nonumber \\&= m_{j} \left[ \frac{|h_{i}|^3 \arctan (\frac{|h_{i}| s}{m_{j}R}) }{m_{j}} + \frac{1}{2} (3 h_{i}^2+m_{j}^2)\ln (s+R)+\frac{1}{2} sR \right] |_{s_{0}}^{s_{1}} \nonumber \\&= |h_{i}|^3 \left( \arctan \frac{|h_{i}| s_{1}}{m_{j} R_{1}} - \arctan \frac{|h_{i}| s_{0}}{m_{j} R_{0}}\right) \nonumber \\&\quad+ \frac{1}{2}m_{j}(3 h_{i}^2+m_{j}^2) \ln \frac{s_{1}+R_{1}}{s_{0}+R_{0}} + \frac{1}{2}m_{j} (s_{1}R_{1}-s_{0}R_{0}) \end{aligned}$$

(52)

In the above two equations, $m_{j}=({\mathbf {r}}-{\mathbf {o}})\cdot \hat{\mathbf {m}}_{j}$ for ${\mathbf {r}}\in C_{j}$, therefore $m_{j}$ can take both positive and negative values. When the observation site ${\mathbf {r}}^{\prime }$ is located on an edge $C_{j}$ of the plane $\partial H_{i}$, that is, $m_{j}=0$ and $h_{i}=0$, the above two integrals are free of singularities as we simply have $B_{j}^1=0$ and $B_{j}^3=0$. In Eq. (52), as $\frac{\arctan {1/m_{j}}}{m_{j}}$ is an even function with respect to $m_{j}$, the sign of $m_{j}$ does not affect the value of the function.