Replacing the Singlet Spinor of the EPR-B Experiment in the Configuration Space with Two Single-Particle Spinors in Physical Space

Abstract

Recently, for spinless non-relativistic particles, Norsen (Found Phys 40:1858–1884, 2010) and Norsen et al. (Synthese 192:3125–3151, 2015) show that in the de Broglie–Bohm interpretation it is possible to replace the wave function in the configuration space by single-particle wave functions in physical space. In this paper, we show that this replacment of the wave function in the configuration space by single-particle functions in the 3D-space is also possible for particles with spin, in particular for the particles of the EPR-B experiment, the Bohm version of the Einstein–Podolsky–Rosen experiment.

Appendix: Spin “Measurement ” in the Stern–Gerlach Experiment

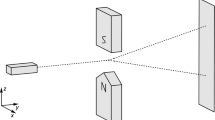
The measurement of spin of a silver atom is carried out by a Stern–Gerlach apparatus: an electromagnet A, where there is a strongly inhomogeneous magnetic field, followed by a screen P (Fig. 4). In the Stern–Gerlach experiment, silver atoms contained in the oven E are heated to a high temperature and escape through a narrow opening. A second aperture, T, selects those atoms whose velocity, $v_0$, is parallel to the y-axis. The atomic beam passes through the gap of the electromagnet A, before condensing on the screen P on two spots of equal intensity $N^{+}$ and $N^{-}$. The magnetic moment of each silver atom before crossing the electromagnet is oriented randomly (isotropically).

Fig. 4

Schematic configuration of a Stern–Gerlach apparatus

In the beam, we represent the atoms by their wave function; one can assume that at the entrance to the electromagnet A (at the initial time $t=0$), each atom can be approximatively described by a Gaussian spinor in x and z:

$$\begin{aligned} \Psi ^{0}(x,z) = (2\pi \sigma _{0}^{2})^{-\frac{1}{2}} e^{-\frac{x^2 +z^2}{4\sigma _0^2}} \left( \begin{array}{l} \cos \frac{\theta _0}{2}e^{ i\frac{\varphi _0}{2}} \\ \sin \frac{\theta _0}{2}e^{-i\frac{\varphi _0}{2}} \end{array} \right) \end{aligned}$$

(30)

corresponding to a pure state. The variable y is treated in a classical way with $y=v_0 t$.

In (30), $\theta _0$ and $\varphi _0$ characterize the initial orientation of the spin. This initial orientation being randomized, on may suppose that $\theta _0$ is drawn in a uniform law from [0, $\pi$] and that $\varphi _0$ is drawn in a uniform law from [0, 2$\pi$]; In this way, we obtain a beam of atoms in which each atom has a different spinor: this is a model of a mixture of pure states.

In the Copenhagen interpretation, it is not necessary to resolve the Pauli equation. Just applying the postulates of quantum-mechanics measurement is sufficient. For measurement of the spin along the z-axis, the postulate of quantification states that the measurement corresponds to an eigenvalue of the spin operator $S_z =\frac{\hbar }{2}\sigma _z$, and the spectral decomposition postulate states that Eq. (7) gives probability $cos^2 \frac{\theta }{2}$ (resp. $sin^2 \frac{\theta }{2}$) to measure the particle in the spin state $+ \frac{\hbar }{2}$ (resp.$-\frac{\hbar }{2}$).

In the de Broglie–Bohm interpretation, the postulates of quantum mechanics measurement are not used, but demonstrated (see below). The results of the measurement are obtained, first by calculating the evolution of the wave function in interaction with the measuring apparatus with the Pauli equation (Eq. 1), secondly by using the calculation of the wave function in space and time to pilot the particle (Eq. 2).

Let us consider the evolution of the initial wave function (5) in the Stern–Gerlach apparatus. To obtain an explicit solution to the Stern–Gerlach experiment, we take the numerical values used in the Cohen–Tannoudji textbook [15]. For a silver atom, we have $m = 1.8 \times 10^{-25}$ kg, $v_0 = 500$ m/s , $\sigma _0$=10$^{-4}$ m. For the electromagnetic field $\mathbf {B}$, $B_{x}=B'_{0} x$; $B_{y}=0$ and $B_{z}=B_{0} -B'_{0} z$ with $B_{0}=5$ T, $B'_{0}=\left| \frac{\partial B}{\partial z}\right| =- \left| \frac{\partial B}{\partial x}\right| = 10^3$ T/m over a length $\Delta l=1$ cm.

The variable y will be treated classically with $y=v_0t$. The particle stays within the magnetic field for a time $\Delta t= \frac{\Delta l}{v_0}=2 \times 10^{-5}s$. On exiting the magnetic field, the particle is free until it reaches screen P placed at a $D=20$ cm distance.

During this time $[0,\Delta t]$, the spinor is calculated (Dürr et al. [7], Gondran [18]) with the Pauli equation (1), where $\mu =\frac{e\hbar }{2m_e}$ is the Bohr magneton:

$$\begin{aligned} \Psi (x,z,t)\simeq \left( \begin{array}{ll} \cos \frac{\theta _0}{2} (2\pi \sigma _0^2)^{-\frac{1}{2}} e^{-\frac{(z-\frac{\mu _{B} B'_{0}}{2 m}t^{2})^2 + x^2}{4\sigma _0^2}} e^{i\frac{\mu _{B} B'_{0}t z -\frac{\mu ^2_{0} B'^2_{0}}{6 m}t^3 + \mu _B B_0 t + \frac{\hbar \varphi _0}{2}}{\hbar }}\\ i \sin \frac{\theta _0}{2} (2\pi \sigma _0^2)^{-\frac{1}{2}} e^{-\frac{(z+\frac{\mu _{B} B'_{0}}{2 m}t^{2})^2 + x^2}{4\sigma _0^2}} e^{i\frac{-\mu _B B'_{0}t z -\frac{\mu ^2_{0} B'^2_{0}}{6 m}t^3 - \mu _B B_0 t -\frac{\hbar \varphi _0}{2}}{\hbar }} \end{array} \right) \nonumber \\ \end{aligned}$$

(31)

After the magnetic field, at time $t+ \Delta t$ $(t \ge 0)$, in the free space, the spinor becomes [18]

$$\begin{aligned} \Psi (x,z,t+\Delta t)\simeq \left( \begin{array}{l} \cos \frac{\theta _0}{2}(2\pi \sigma _0^2)^{-\frac{1}{2}} e^{-\frac{(z-z_{\Delta }- ut)^2 + x^2}{2\sigma _0^2}} e^{i\frac{m u z + \hbar \varphi _+}{\hbar }} \\ i \sin \frac{\theta _0}{2} (2\pi \sigma _0^2)^{-\frac{1}{2}} e^{-\frac{(z+z_{\Delta }+ ut)^2+ x^2}{2\sigma _0^2}}e^{i\frac{- muz + \hbar \varphi _-}{\hbar }} \end{array} \right) \end{aligned}$$

(32)

where

$$\begin{aligned} z_{\Delta }=\frac{\mu _B B'_{0}(\Delta t)^{2}}{2 m}=10^{-5}m,~~~~~~u =\frac{\mu _B B'_{0}(\Delta t)}{m}=1 m/s. \end{aligned}$$

(33)

Equation (32) takes into account the spatial extension of the spinor and we note that the two-spinor components have very different values.

Since we have a mixture of pure states, the atomic density $\rho (z,t+\Delta t)$ is found by integrating $\rho (x, z,t+\Delta t)$ on x and on ($\theta _0$, $\varphi _0$):

$$\begin{aligned} \rho (z,t+ \Delta t)&= (2\pi \sigma _0^2)^{-\frac{1}{2}} \frac{1}{2}\left( e^{-\frac{(z-z_{\Delta }- ut)^2}{2\sigma _0^2}}+ e^{-\frac{(z+z_{\Delta }+ ut)^2}{2\sigma _0^2}}\right) . \end{aligned}$$

(34)

The decoherence time $t_D$, where the beam is separated into the two spots $N^{+}$ and $N^{-}$ (when $z_{\Delta } +u t_D \geqslant 3\sigma _0$), is then given by the equation:

$$\begin{aligned} t_{D} \simeq \frac{3 \sigma _{0}-z_\Delta }{u}=3 \times 10^{-4}s. \end{aligned}$$

(35)

We then obtain atoms with spins oriented only along the z-axis (positively or negatively). Experimentally, we do not measure the spin directly, but position ($\widetilde{x}$, $\widetilde{z}$) of the particle impact on P. If $\widetilde{z}\in N^+$, the term $\psi ^-$ of (32) is numerically equal to zero, and the spinor $\Psi$ is proportional to $\left( {\begin{array}{c}1\\ 0\end{array}}\right)$, one of the eigenvectors of $\sigma _z$:

$$\begin{aligned} \Psi (\tilde{z},t+\Delta t) \simeq (2\pi \sigma _0^2)^{-\frac{1}{4}} \cos \frac{\theta _0}{2} e^{-\frac{(\tilde{z}-z_{\Delta }- ut)^2 + \tilde{x}^2}{4\sigma _0^2}} e^{i\frac{m u \tilde{z} + \hbar \varphi _+}{\hbar }}\left( \begin{array}{l} 1 \\ 0 \end{array} \right) . \end{aligned}$$

If $\widetilde{z}\in N^-$, the term $\psi ^+$ of (32) is numerically equal to zero and the spinor $\Psi$ is proportional to $\left( {\begin{array}{c}0\\ 1\end{array}}\right)$, the other eigenvector of $\sigma _z$:

$$\begin{aligned} \Psi (\tilde{z},t+\Delta t) \simeq (2\pi \sigma _0^2)^{-\frac{1}{4}}\sin \frac{\theta _0}{2} e^{-\frac{(\tilde{z}+z_{\Delta }+ ut)^2+ \tilde{x}^2}{4\sigma _0^2}} e^{i\frac{- mu\tilde{z} + \hbar \varphi _-}{\hbar }}\left( \begin{array}{l} 0 \\ 1 \end{array} \right) . \end{aligned}$$

Therefore, the measurement of the spin corresponds to an eigenvalue of the spin operator $S_z= \frac{\hbar }{2} \sigma _z$. It is a proof of the postulate of quantization in Bohmian mechanics.

Equation (32) gives the probability $\cos ^{2} \frac{\theta _0}{2}$ (resp.$\sin ^{2} \frac{\theta _0}{2}$) of measuring the particle in the spin state $+ \frac{\hbar }{2}$ (resp.$- \frac{\hbar }{2}$). It is a proof of the spatial decomposition postulate in Bohmian mechanics.

Figure 5 presents in x0y a set of 10 silver-atom trajectories of which initial characteristics $(\theta _0$,$\varphi _0$,$z_0$) have been randomly chosen: $\theta _0$ and $\varphi _0$, which define on one hand the wave function, have uniform distributions, and $z_0^A$, which on the other hand defines the particle position in the wave function, has a normal distribution $\mathcal {N}(0,\sigma _{0})$. This double representation of quantum particles allows to take into account a mixture of pure states which satisfies the density of (34). Spin orientation $\theta (z(t),t)$ is represented by arrows.

Fig. 5

10 silver atom trajectories after the electro-magnet where the initial characteristics $(\theta _0$,$\varphi _0$,$z_0$) have been randomly chosen; Arrows represent the spin orientation $\theta (z(t),t)$

We can see that the final orientation, obtained after the decoherence time $t_{D}$, will depend on the initial particle position $z_{0}^A$ in the wave packet and on the initial angle $\theta _{0}^A$ of the atom magnetic moment with the z axis.

Finally, we can also give a clear explanation of the Albert’s example on contextuality [23, pp. 153–155]. He considers a Stern–Gerlach experiment where the initial wave function is a pure state with symmetric spin orientation ($\theta _0 =\dfrac{\pi }{4}$ and so $z^{\theta _0}=0$). He changes, in a second experiment, the orientation of the magnetic field inside the Stern–Gerlach apparatus ($\mathbf {B}$ into $-\mathbf {B}$). For the same initial position of atoms ( for example $z_0 > 0$), the first experiment gives a spin + and, in the second, a spin $-$. Bohmian mechanics explains this result: u and $z_{\Delta }$ are proportional to $B'_0 =\dfrac{\partial B_{z}}{\partial z}$ (Eq. 33), and therefore change their signs like $\mathbf {B}$. By solving the Pauli equation, Bohmian mechanics is naturally contextual (involves the measuring device).