Skip to main content
SpringerLink
Log in

Order and rack sequencing in a robotic mobile fulfillment system with multiple picking stations

  • Published:
Flexible Services and Manufacturing Journal Aims and scope Submit manuscript

Abstract

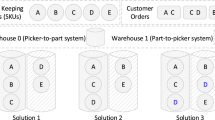
The robotic mobile fulfillment system, where mobile robots carry racks to stationary stations for human pickers, is widely used in e-commerce warehouses. The operational efficiency of the system is largely affected by the organization of the order picking process. In this paper, we investigate an order picking tactic in a robotic mobile fulfillment system that allows racks moving between multiple picking stations in order to feed more orders during one visit and therefore save the overall throughput time. To evaluate this operational tactic’s effectiveness, we propose a mathematical model to jointly optimize the order assignment, order sequencing, rack selection, and rack sequencing. A two-stage hybrid heuristic algorithm framework is then presented, including order assignment in the first stage and order and rack sequencing in the second stage. We conduct numerical experiments to validate the proposed algorithms’ performance under different strategies and find out that the inter-station operation can significantly save order throughput time on the testing cases. We also investigate the effects of several factors, including the number of picking stations, their capacities, the stock keeping unit diversity, and queue length. Furthermore, a solid simulation is carried out to show the rationale of using rack moves as the objective rather than the completion time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Azadeh K, De Koster R, Roy D (2019) Robotized and automated warehouse systems: review and recent developments. Transp Sci 53(4):917–945

    Article  Google Scholar 

  • Bartholdi III JJ, Hackman ST (2008) Warehouse and distribution science. Supply Chain and Logistics Institute, School of Industrial and Systems Engineering, Georgia Institute of Technology. https://www.scl.gatech.edu/sites/default/files/downloads/gtsclwarehouse_science_bartholdi.pdf

  • Boysen N, Briskorn D, Emde S (2017) Parts-to-picker based order processing in a rack-moving mobile robots environment. Eur J Opera Res 262(2):550–562

    Article  MathSciNet  MATH  Google Scholar 

  • Boysen N, Briskorn D, Emde S (2017) Sequencing of picking orders in mobile rack warehouses. Eur J Opera Res 259(1):293–307

    Article  MathSciNet  MATH  Google Scholar 

  • Boysen N, Fedtke S, Weidinger F (2018) Optimizing automated sorting in warehouses: the minimum order spread sequencing problem. Eur J Opera Res 270(1):386–400

    Article  MathSciNet  MATH  Google Scholar 

  • Boysen N, de Koster R, Weidinger F (2019) Warehousing in the e-commerce era: a survey. Eur J Opera Res 277(2):396–411

    Article  MathSciNet  MATH  Google Scholar 

  • Bozer YA, Aldarondo FJ (2018) A simulation-based comparison of two goods-to-person order picking systems in an online retail setting. Int J Prod Res 56(11):3838–3858

    Article  Google Scholar 

  • De Koster R, Le-Duc T, Roodbergen KJ (2007) Design and control of warehouse order picking: a literature review. Eur J Opera Res 182(2):481–501

    Article  MATH  Google Scholar 

  • Duan G, Zhang C, Gonzalez P, Qi M (2021) Performance evaluation for robotic mobile fulfillment systems with time-varying arrivals. Comp Ind Eng 158:107365

    Article  Google Scholar 

  • Füßler D, Boysen N (2019) High-performance order processing in picking workstations. EURO J Transp Logist 8(1):65–90

    Article  Google Scholar 

  • Grosse EH, Glock CH, Jaber MY, Neumann WP (2015) Incorporating human factors in order picking planning models: framework and research opportunities. Int J Prod Res 53(3):695–717

    Article  Google Scholar 

  • Gu J, Goetschalckx M, McGinnis LF (2007) Research on warehouse operation: a comprehensive review. Eur J Opera Res 177(1):1–21

    Article  MATH  Google Scholar 

  • Huang GQ, Chen MZ, Pan J (2015) Robotics in ecommerce logistics. HKIE. Transactions 22(2):68–77

    Google Scholar 

  • Jaghbeer Y, Hanson R, Johansson MI (2020) Automated order picking systems and the links between design and performance: a systematic literature review. Int J Prod Res 58(15):4489–4505

    Article  Google Scholar 

  • Lamballais T, Roy D, De Koster MBM (2019) Inventory allocation in robotic mobile fulfillment systems. IISE Transactions pp 1–17

  • Li Z, Li W (2015) Mathematical model and algorithm for the task allocation problem of robots in the smart warehouse. Am J Opera Res 5(06):493

    Article  Google Scholar 

  • Li ZP, Zhang JL, Zhang HJ, Hua GW (2017) Optimal selection of movable shelves under cargo-to-person picking mode. Int J Simul Modell 16(1):145–156

    Article  Google Scholar 

  • Menéndez B, Pardo EG, Alonso-Ayuso A, Molina E, Duarte A (2016) Variable neighborhood search strategies for the order batching problem. Comp Opera Res 78:500–512

    Article  MathSciNet  MATH  Google Scholar 

  • Merschformann M, Lamballais T, Koster MBMD, Suhl L (2019) Decision rules for robotic mobile fulfillment systems. Opera Res Perspect 6:100128

    Article  MathSciNet  Google Scholar 

  • Mladenović N, Hansen P (1997) Variable neighborhood search. Comp Opera Res 24(11):1097–1100

    Article  MathSciNet  MATH  Google Scholar 

  • Öncan T (2015) Milp formulations and an iterated local search algorithm with tabu thresholding for the order batching problem. Euro J Opera Res 243(1):142–155

    Article  MathSciNet  MATH  Google Scholar 

  • QuickTron (2020) Quicktron. http://www.flashhold.com/english.php

  • Roy D, Nigam S, de Koster R, Adan I, Resing J (2019) Robot-storage zone assignment strategies in mobile fulfillment systems. Transp Res Part E: Logist Transp Rev 122:119–142

    Article  Google Scholar 

  • Scholz A, Schubert D, Wäscher G (2017) Order picking with multiple pickers and due dates-simultaneous solution of order batching, batch assignment and sequencing, and picker routing problems. Euro J Opera Res 263(2):461–478

    Article  MathSciNet  MATH  Google Scholar 

  • Tanimoto TT (1957) Ibm internal report. Nov 17:1957

  • Valle CA, Beasley JE (2021) Order allocation, rack allocation and rack sequencing for pickers in a mobile rack environment. Computers & Operations Research 125:105090

    Article  MathSciNet  MATH  Google Scholar 

  • Weidinger F, Boysen N, Briskorn D (2018) Storage assignment with rack-moving mobile robots in kiva warehouses. Transp Sci 52(6):1479–1495

    Article  Google Scholar 

  • Wurman PR, D’Andrea R, Mountz M (2008) Coordinating hundreds of cooperative, autonomous vehicles in warehouses. AI Magaz 29(1):9–9

    Google Scholar 

  • Xi X, Liu C, Miao L (2018) Storage assignment and order batching problem in kiva mobile fulfilment system. Eng Optim 50(11):1941–1962

    Article  MathSciNet  MATH  Google Scholar 

  • Yuan R, Graves SC, Cezik T (2019) Velocity-based storage assignment in semi-automated storage systems. Prod Opera Manag 28(2):354–373

    Article  Google Scholar 

  • Zhang J, Yang F, Weng X (2019) A building-block-based genetic algorithm for solving the robots allocation problem in a robotic mobile fulfilment system. Mathematical Problems in Engineering 2019

  • Zou B, Gong YY, Xu X, Yuan Z (2017) Assignment rules in robotic mobile fulfilment systems for online retailers. Int J Prod Res 55(20):6175–6192

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Key R&D Program of China under grant No. 2018AAA0101705, the National Natural Science Foundation of China under Grant No. 71772100, and Shenzhen Science and Technology Project under Grant No. JCYJ20170412171044606, and Sichuan Science and Technology Program under grant No. 2021JDRC0009.

Author information

Authors and Affiliations

  1. Research Center on Modern Logistics, Shenzhen International Graduate School, Tsinghua University, Shenzhen, 518055, China

    Bingqian WANG

  2. The Civil Aviation Logistics Technology Co., Ltd., The Second Research Institute of Civil Aviation Administration of China, Chengdu, 610041, China

    Xiuqing YANG

  3. Research Center on Modern Logistics, Shenzhen International Graduate School, Tsinghua University, Shenzhen, 518055, China

    Mingyao QI

Authors
  1. Bingqian WANG
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiuqing YANG
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mingyao QI
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mingyao QI.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A RS-Greedy

We denote the difference between rack j and the current in-process orders as DiffVector(j), then the pseudocode of the RS-Greedy is depicted in Algorithm 3 where PickingOrderSet, RemainingOrderSet and DiffMatrix have the same meaning as in OS-Greedy, and RackSet is the set of all racks. According to the algorithmic procedure, orders are extracted from the given OrderSequence successively, while the rack with the minimum difference with all the in-process orders (excluding those finished SKUs) and free of conflict is selected to visit the PS one by one. Completed orders will be removed and replaced by new orders. Until the SKUs contained on the current picking orders cannot be fulfilled anymore by the current rack, a new rack will be selected, so on so forth.

figure c

Appendix B Psudeocode of RS-VNS

figure d

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

WANG, B., YANG, X. & QI, M. Order and rack sequencing in a robotic mobile fulfillment system with multiple picking stations. Flex Serv Manuf J 35, 509–547 (2023). https://doi.org/10.1007/s10696-021-09433-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10696-021-09433-8

Keywords

Search

Navigation