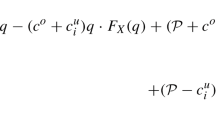Abstract
This paper considers the problem of hedging inventory risk for a seasonal product whose demand is sensitive to weather conditions, such as the average seasonal temperature. The newsvendor not only decides the order quantity, but also adopts a weather hedging strategy. A typical hedging strategy is to use an option (weather derivative) that is constructed on a weather index before the season begins, which will compensate the buyer of the option if the actual seasonal weather index is above (or below) a given strike level. We adopt the risk measure of Conditional-Value at Risk (\(\hbox{CVaR}\)) and explore the joint decision problem in mean-CVaR criterion. We find that the weather derivative hedging can increase order quantity. Furthermore, it can help the risk-averse newsvendor improve both expected overall and downside profits.


Similar content being viewed by others
Notes
Examples of catastrophic weather conditions include natural disaster type weathers, such as cyclonic storms, tornados, blizzards, etc.
For example, \(D(\epsilon, t)=a-bt+\epsilon, b>0\) and \(D(\epsilon, t)=(a-bt)\epsilon, b>0 \epsilon>0\), for which the correlation between the demand and temperature t is \(\rho={\frac{-b\sigma_t}{\sqrt{b^2\sigma_t^2+\sigma_\epsilon^2}}}\) and \(\rho={\frac{-b \mu_\epsilon \sigma_t}{\sigma_{D(\epsilon, t)}}}\) respectively, where σ stands for standard deviation and μ stands for expected value. We see that the demand is negatively correlated with temperature t.
References
Acerbi C, Tasche D (2002a) On the coherence of expected shortfall. J Bank Finance 26:1487–1503
Acerbi C, Tasche D (2002b) Expected shortfall: a natural coherent alternative to value at risk. Econ Notes 31:379–388
Agrawal V, Seshadri S (2002) Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem. Manufact Service Oper Manage 2:410–423
Ahmed S, Cakmak U, Shapiro A (2007) Coherent risk measures in inventory problems. Eur J Oper Res 182:226–238
Artzner P, Delbaen F, Eber JM, Heath D (1999) Coherent measures of risk. Math Finance 9:203–228
Baccardax M (2002) The temperature’s rising. http://www.cfoeurope.com/displaystory.cfm/1738060. Accessed 5 May 2006
Baker B, Petrillo N (2004) Value of weather risk management contracts reaches all-time high. http://www.wrma.org/wrma/library/file677.doc. Accessed 29 March 2010
Bouakiz M, Sobel MJ (1992) Inventory control with an expected utility criterion. Oper Res 40:603–608
Boyabatli O, Toktay LB (2004) Operational hedging: a review with discussion. Working paper, INSEAD, France
Caldentey R, Haugh M (2006) Optimal control and hedging of operations in the presence of financial markets. Math Oper Res 31:285–304
Cao M, Wei J (2004) Weather derivatives valuation and market price of weather risk. J Fut Markets 24:1065–1089
Chen F, Federgruen A (2000) Mean-variance analysis of basic inventory models. Working paper, Graduate School of Business, Columbia University
Chen Y, Yano CA (2010) Improving supply chain performance and managing risk under weather-related demand uncertainty. Manage Sci 56: 1380-1397
Chen Y, Xu M, Zhang G (2006) A risk-averse newsvendor model under the CVaR decision criterion. Oper Res (forthcoming)
Chen X, Sim M, Simchi-Levi D, Sun P (2007) Risk aversion in inventory management. Oper Res 55: 828–842
Chod J, Rudi N, Van Mieghem JA (2006) Operational flexibility and financial hedging: complements or substitutes? Working paper
Choi S, Ruszczynski A (2007) A risk-averse newsvendor with law invariant coherent measures of risk. Oper Res Lett (forthcoming)
Ding Q, Dong L, Kouvelis P (2004) On the integration of production and financial hedging decisions in global markets. Oper Res (forthcoming)
Dischel B (2001) Weather risk management at the frozen falls fuel company. http://www.cmegroup.com/trading/weather/files/WEA_weather_risk.pdf. Accessed 29 March 2010
Dischel B, Barrieu P (2001) Weather hedging at the hot air gas comapny. Electronic Journal: Erivativesreview.com
Eeckhoudt L, Gollier C (1995) Schlesinger H. Risk averse (and prudent) newsboy. Manage Sci 41:786–794
Gaur V, Seshadri S (2005) Hedging inventory risk through market instruments. Manufact Service Oper Mange 7:103–120
Gotoh J, Takano Y (2007) The downside risk-averse newsvendor minimizing conditional value-at-risk. Eur J Oper Res 179:80–96
Harrington S, Niehaus G (2003) United grain growers: enterprise risk management and weather risk. Risk Manage Insurance Rev 6:193–208
Hull J (2003) Options, futures, and other derivatives, 5th edn. Prentice Hall, Singapore
Jewson S (2003) Closed-form expressions for the pricing of weather derivatives: part 1-the expected payoff. Availabe at Social Science Research Network. http://ssrn.com/abstract=436262
Jewson S, Brix A (2005) Weather derivative valuation. Cambridge University Press, Cambridge
Jewson S, Rodrigo C (2002) The use of weather forecasts in the pricing of weather derivatives. Availabe at Social Science Research Network. http://ssrn.com/abstract=405780
Jorion P (2006) Value at risk: a new benchmark for managing financial risk. McGraw Hill, New York
Lau H (1980) The newboy problem under alternative optimization objectives. J Oper Res Soc 31:525–535
Li D, Ng WL (2000) Optimal dynamic portfolio selection: multi-period mean-variance formulation. Math Finance 10:387–406
Malinow M (2002) End-users (chapter 5). In: Banks E (ed) Weather risk management. Palgrave, New York
Markowitz H (1952) Portfolio selection. J Finance 7:77-91
Oum Y, Oren S, Deng S (2006). Hedging quantity risks with standard power options in a competitive wholesale electricity market. Naval Res Logist 53:697–712
Rathke M (2005) Weather exposure of the beverage industry. The Meteo Consult Group, MC-Wetter GmbH. http://www.knmi.nl/mureau/ECAM/Economy/Rathke.pdf. Accessed 29 March 2010
Rockafellar RT, Uryasev S (2000) Optimization of conditional value-at-risk. J Risk 2:21–42
Rockafellar RT, Uryasev S (2002) Conditional value-at-risk for general loss distributions. J Bank Finance 26:1443–1471
Seifert RW, Thonemann UW, Hausman WH (2004) Optimal procurement strategies for online spot markets. Eur J Oper Res 152:781–799
Speedwell Weather Derivatives Ltd (2003) How a fleece jacket manufacturer uses a PUT to protect against a mild winter. http://www.weatherderivs.com/ WDExamples.htm. Accessed 23 Oct 2007
Szegö G (2002) Measure of risk. J Bank Finance 26:1253–1272
WRMA: Weather Risk Management Association (2006) Trading weather risk: 2005/06 survey (April 2005–March 2006). http://www.wrma.org/wrma/index.php?option=com_content&task=view&id=74&Itemid=33. Accessed 12 Nov 2006
Acknowledgments
The authors are grateful to the Editor in Chief Professor Hans-Otto Guenther, the anonymous SE and two reviewers for their constructive comments. The authors also benefited from discussions with Professors Minghui Xu, Simai He, Janny Leung and Sridhar Seshadri. The research of Frank Y. Chen was supported in part by the Hong Kong Research Grants Council under grant no. CUHK411105. The research of Xiuli Chao was partially supported by the NSF under CMMI-0800004 and CMMI-0927631.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Lemma 1
For any \(\lambda \in[0,1]\), and any two different points \((Q_1,n_1,v_1)\) and \((Q_2,n_2,v_2)\),
As \(\Uppi(Q,n,D(t))\) is jointly concave in (Q, n),
Hence,
the last inequality holds due to the convexity of function \([\cdot]^{+}\).
Then, substituting the above inequality into (13) yields
Thus, F β(Q, n, v) is jointly concave in (Q, n, v). \(\square\)
Proof of Proposition 1
Note the objective in (11) for the case without option hedging,
Let \(\hat{F}_{(\beta, \lambda)}(Q, v)=\lambda\hbox{E}[\Uppi_1(Q, D(t))]+(1-\lambda)\hat{F}_{\beta}(Q, v)=\lambda\hbox{E}[\Uppi_1(Q, D(t))]+(1-\lambda)\{v-(1-\beta)^{-1}\hbox{E}[v-\Uppi_1(Q, D(t))]^{+}\}.\) Denote by D l(t) and D u(t) the lower and upper bounds of D(t), respectively. For fixed Q,
At the point (p − c)Q,
-
(1)
If \({\frac{\partial^{-} \hat{F}_{(\beta, \lambda)}(Q,v)} {\partial v}}|_{v=(p-c)Q}<0\), the maximizer \(\hat{v}\) of \(\hat{F}_{(\beta, \lambda)}(Q,v)\) satisfies \(\hat{v}<(p-c)Q\) and is determined by
$$ 1-{\frac{1} {1-\beta}}\hbox{E}_{t}\left[\int\limits_{D^{l}(t)}^{{\frac{\hat{v}+(c-s)Q} {p-s}}}g(x;t)dx\right] =0. $$(13)In this case,
$$\begin{aligned} \hat{F}_{(\beta, \lambda)}(Q,\hat{v})= & \lambda\hbox{E}[\pi_1(Q,D(t))] &+(1-\lambda)\left\{\hat{v}-(1-\beta)^{-1}\hbox{E}_{t}\left[\int\limits_{D^{l}(t)}^{{\frac{\hat{v}+(c-s)Q} {p-s}}}(\hat{v} +(c-s)Q-(p-s)x)g(x;t)dx\right]\right \} \\ {\frac{d\hat{F}_{(\beta, \lambda)}(Q, \hat{v})}{d Q}} &= {\frac{\partial \hat{F}_{(\beta, \lambda)}(Q, \hat{v})} {\partial Q}}+{\frac{\partial \hat{F}_{(\beta, \lambda)}(Q, \hat{v})} {\partial v}} \frac{\partial \hat{v}}{\partial Q}\\ &=\lambda\{-c+s+(p-s)\hbox{E}[1_{D(t)> Q}]\} +(1-\lambda) \left\{(1-\beta)^{-1}(-c+s)\hbox{E}_{t} \left[\int\limits_{D^{l}(t)}^{{\frac{\hat{v}+(c-s)Q} {p-s}}}g(x;t)dx\right]\right\}+0\\ &=\lambda\{-c+s+(p-s)\hbox{E}[1_{D(t)> Q}]\}+(1-\lambda)(-c+s)\\ &=\lambda\{-c+s+(p-s)(1-\hbox{E}_{t}[G(Q; t)])\}+(1-\lambda)(-c+s)\\ &=\lambda(p-c)-\lambda(p-s)\hbox{E}_{t}[G(Q; t)]-(1-\lambda)(c-s). \end{aligned}$$Then \(\hat{Q}\) satisfies \(\hbox{E}_{t}[G(\hat{Q}; t)]={\frac{\lambda (p-c)-(1-\lambda)(c-s)}{\lambda (p-s)}}=1-{\frac{c-s}{\lambda (p-s)}}\), where \(\lambda >{\frac{c-s}{\beta (p-s)}}\) to make the condition \({\frac{\partial^{-} \hat{F}_{(\beta, \lambda)}(\hat{Q},v)}{\partial v}}|_{v=(p-c)\hat{Q}}<0\) hold true.
-
(2)
If \({\frac{\partial^{-} \hat{F}_{(\beta, \lambda)}(Q,v)}{\partial v}}|_{v=(p-c)Q}\ge 0\), note that the auxiliary function is concave in v, then \(\hat{v}=(p-c)Q\). In this case,
$$ \hat{F}_{(\beta, \lambda)}(Q, (p-c)Q)=\lambda\hbox{E}[\Uppi_1(Q, D(t))] +(1-\lambda)\left\{(p-c)Q-(1-\beta)^{-1}\hbox{E}_{t}\left[\int\limits_{D^{l}(t)}^{Q}((p-s)Q -(p-s)x)g(x;t)dx\right]\right \} , $$then
$$ \begin{aligned}{\frac{d\hat{F}_{(\beta,\lambda)}(Q, (p-c)Q)}{d Q}}&=\lambda \{-c+s+(p-s)\hbox{E}[1_{D(t)> Q}]\} +(1-\lambda)\left\{(p-c)-(1-\beta)^{-1}(p-s)\hbox{E}_{t}\left[\int\limits_{D^{l}(t)}^{Q}g(x; t)dx\right]\right\} \\ &= \lambda\{-c+s+(p-s)(1-\hbox{E}_{t}[G(Q; t)])\} +(1-\lambda)\{(p-c)-(1-\beta)^{-1}(p-s)\hbox{E}_{t}[G(Q; t)]\}\\ &=(p-c)-(\lambda +(1-\lambda)(1-\beta)^{-1})(p-s)\hbox{E}_{t}[G(Q; t)]. \end{aligned} $$Then \(\hat{Q}\) satisfies \(\hbox{E}_{t}[G(\hat{Q}; t)]={\frac{(1-\beta)(p-c)}{(1-\lambda\beta)(p-s)}}\), where \(\lambda \le {\frac{c-s}{\beta (p-s)}}\) to make the condition \({\frac{\partial^{-} \hat{F}_{(\beta, \lambda)}(\hat{Q},v)} {\partial v}}|_{v=(p-c)\hat{Q}}\ge 0\) hold true.
From the above analysis, the optimal order quantity without option hedging under the tradeoff criterion, \(\hat{Q}\), is determined by (12). \(\square\)
We give here Lemma 2 which will be repeatedly used in the proofs of the results to follow.
Lemma 2
Let\(G_{1}(\cdot)\)and\(G_{2}(\cdot)\)be two integrable functions. If they have contrary monotonicity, then\(\hbox{E}[G_1(t)G_2(t)]\le\hbox{E}[G_1(t)]\hbox{E}[G_2(t)]\), and if they have same monotonicity, then\(\hbox{E}[G_1(t)G_2(t)]\ge\hbox{E}[G_1(t)]\hbox{E}[G_2(t)],\)wheretis a continuous random variable.
Proof
If \(G_1(\cdot)\) and \(G_2(\cdot)\) have contrary monotonicity, for any realizations t and s, we have \([G_1(t)-G_1(s)][G_2(t)-G_2(s)]\le 0 \Rightarrow G_1(t) G_2(t)+G_1(s) G_2(s) \le G_1(t) G_2(s)+G_1(s) G_2(t)\). Assuming the density function of t to be \(f(\cdot),\)
i.e., \(\hbox{E}[G_1(t)G_2(t)]\le\hbox{E}[G_1(t)]\hbox{E}[G_2(t)].\) Similarly, if \(G_1(\cdot)\) and \(G_2(\cdot)\) have same monotonicity, it holds that \(\hbox{E}[G_1(t)G_2(t)]\ge\hbox{E}[G_1(t)]\hbox{E}[G_2(t)]\). \(\square\)
Proof of Proposition 4
Note the objective in (7) for the case with option hedging,
Let \(F_{(\beta, \lambda)}(Q,n,v)=\lambda\hbox{E}[\Uppi(Q,n,D(t))]+(1-\lambda)F_{\beta}(Q,n,v)=\lambda\hbox{E}[\Uppi(Q,n, D(t))]+(1-\lambda)\{v-(1-\beta)^{-1}\hbox{E}[v-\Uppi(Q,n,D(t))]^{+}\}. \)
Both \(\Uppi_2(t)\) and \(\hbox{E}_{D}[1_{\Uppi_1(Q,D(t))<v}|t]\) are increasing in t (It is easy to check that for given \(Q, \Uppi_1(Q, \cdot)\) is an increasing function and \(1_{\Uppi_1(Q, \cdot)<v}\) is a decreasing function then \(\hbox{E}_{D}[1_{\Uppi_1(Q,D(t))<v}|t]\) is increasing in t by the assumption that D(t) is stochastically decreasing in t.), so by Lemma 2, if \(\hbox{E}[\Uppi_2(t)]=0\),
By concavity of \(F_{(\beta, \lambda)}(Q,n,v), n^{*}\ge 0\). \(\square\)
Proof of Proposition 5
If \(n>0, {\frac{\partial F_{(\beta, \lambda)}(Q, n, v)}{\partial v}}|_{v=(-c+s)Q+n\Uppi_2^l}=1-\lambda,\) and
From Proposition 1,
-
(1)
If \(\lambda > {\frac{c-s}{\beta (p-s)}}\), then
$$ {\frac{\partial^{-} F_{(\beta,\lambda)}(\hat{Q}, n, v)}{\partial v}}|_{v=(p-c)\hat{Q}+n\Uppi_2^u}\le(1-\lambda)\{1-(1-\beta)^{-1}\hbox{E}_{t}[G(\hat{Q}; t)]\}< 0 $$by noticing that \(\hbox{E}_{t}[1_{\Uppi_2^u>\Uppi_2(t)}(1-G(\hat{Q}; t))]\ge 0.\) Thus, \(v^*(\hat{Q}, n)\in((-c+s)\hat{Q}+n\Uppi^l_2, (p-c)\hat{Q}+n\Uppi^u_2)\), and by (14),
$$ \hbox{E}[1_{v^*(\hat{Q}, n)>\Uppi(\hat{Q},n,D(t))}]=1-\beta; $$ -
(2)
If \(\lambda \le {\frac{c-s}{\beta (p-s)}}\), and if \({\frac{\partial^{-} F_{(\beta, \lambda)}(Q, n, v)}{\partial v}}|_{v=(p-c)\hat{Q}+n\Uppi_2^u}\ge 0\), then \(v^*(\hat{Q}, n)=(p-c)\hat{Q}+n\Uppi^u_2\), and
$$ \begin{aligned} F_{(\beta, \lambda)}(Q, n, v)|_{v=(p-c)Q+n\Uppi_2^u} &= \lambda\hbox{E}[\Uppi(Q,n,D(t))]+(1-\lambda)\{(p-c)Q+n\Uppi_2^u\\ &\quad-(1-\beta)^{-1}\hbox{E}_{t}\left[\int\limits_{D^l(t)}^{Q}((p-s)(Q-x)+n(\Uppi^u_2-\Uppi_2(t))) g(x; t) dx +\int\limits_{Q}^{D^u(t)}n(\Uppi_2^u-\Uppi_2(t))g(x; t)dx]\right \},\\ & {\frac{\partial F_{(\beta, \lambda)}(Q, n, v^*(Q, n))}{\partial Q}}|_{Q=\hat{Q}}&=\lambda \{p-c-(p-s)\hbox{E}_{t}[G(\hat{Q}; t)]\} \quad+(1-\lambda)\left\{(p-c)-(1-\beta)^{-1}(p-s)\hbox{E}_{t}\left[\int\limits_{D^l(t)}^{\hat{Q}}g(x; t)dx\right]\right\}\\ &= (p-c)-{\frac{1-\lambda\beta} {1-\beta}}(p-s)\hbox{E}_{t}[G(\hat{Q}; t)] =0; \end{aligned} $$ -
(3)
If \(\lambda \le {\frac{c-s}{\beta (p-s)}}\), and \({\frac{\partial^{-} F_{(\beta, \lambda)}(Q, n, v)}{\partial v}}|_{v=(p-c)\hat{Q}+n\Uppi_2^u}<0\), then \(v^*(\hat{Q}, n)\in((-c+s)\hat{Q}+n\Uppi^l_2, (p-c)\hat{Q}+n\Uppi^u_2)\), and
$$ \hbox{E}[1_{v^*(\hat{Q}, n)>\Uppi(\hat{Q},n,D(t))}]=1-\beta. $$
For the cases (1) and (3), i.e., \(\hbox{E}[1_{v^*(\hat{Q}, n)>\Uppi(\hat{Q},n,D(t))}]=1-\beta,\)
When \(\lambda >{\frac{c-s}{\beta (p-s)}}, \hbox{E}_{t}[G(\hat{Q}; t)]={\frac{\lambda (p-c)-(1-\lambda)(c-s)}{\lambda (p-s)}}\), and
When \(\lambda \le {\frac{c-s}{\beta (p-s)}}, \hbox{E}_{t}[G(\hat{Q}; t)]={\frac{(1-\beta)(p-c)}{(1-\beta \lambda)(p-s)}}\), and
In all, for all cases (1), (2) and (3), \({\frac{\partial F_{(\beta, \lambda)}(Q,n,v^*(Q,n))}{\partial Q}}|_{Q=\hat{Q}}\ge 0\).
When n < 0, similar analysis can be conducted by inter-changing the roles of \(\Uppi_2^l\) and \(\Uppi_2^u\) in the above proof, and when n = 0,
By concavity of F (β, λ)(Q, n, v), we have \(Q^*\ge \hat{Q}\). This completes the proof.
Note the condition in this proposition, G(y;t) is strictly increasing in y for given t, is to get a unique solution \(\hat{Q}\) for the unhedged case. Generally without this condition, assume \(\hat{Q}\) and Q * are the largest solutions for the unhedged and hedged cases respectively, we still have the result that \(Q^*\ge \hat{Q}.\) \(\square\)
Rights and permissions
About this article
Cite this article
Gao, F., Chen, F.Y. & Chao, X. Joint optimal ordering and weather hedging decisions: mean-CVaR model. Flex Serv Manuf J 23, 1–25 (2011). https://doi.org/10.1007/s10696-011-9078-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10696-011-9078-3