Using scan statistics for congenital anomalies surveillance: the EUROCAT methodology

Abstract

Scan statistics have been used extensively to identify temporal clusters of health events. We describe the temporal cluster detection methodology adopted by the EUROCAT (European Surveillance of Congenital Anomalies) monitoring system. Since 2001, EUROCAT has implemented variable window width scan statistic for detecting unusual temporal aggregations of congenital anomaly cases. The scan windows are based on numbers of cases rather than being defined by time. The methodology is imbedded in the EUROCAT Central Database for annual application to centrally held registry data. The methodology was incrementally adapted to improve the utility and to address statistical issues. Simulation exercises were used to determine the power of the methodology to identify periods of raised risk (of 1–18 months). In order to operationalize the scan methodology, a number of adaptations were needed, including: estimating date of conception as unit of time; deciding the maximum length (in time) and recency of clusters of interest; reporting of multiple and overlapping significant clusters; replacing the Monte Carlo simulation with a lookup table to reduce computation time; and placing a threshold on underlying population change and estimating the false positive rate by simulation. Exploration of power found that raised risk periods lasting 1 month are unlikely to be detected except when the relative risk and case counts are high. The variable window width scan statistic is a useful tool for the surveillance of congenital anomalies. Numerous adaptations have improved the utility of the original methodology in the context of temporal cluster detection in congenital anomalies.

Appendix: The scan statistic defined by Nagarwalla [11]

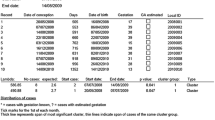
An analysis requires the dates of a set of cases, and the specification of the start and end dates for the analysis period. For a given subset of n cases occurring between date _start and date _end , it is possible to calculate the test statistic lambda as follows:

$$\lambda = \left( \frac{n}{r} \right)^{n} \left( {\frac{r - n}{n}} \right)^{r - n} \left( \frac{1}{d} \right)^{n} \left( {\frac{1}{1 - d}} \right)^{r - n}$$

Where r is the total number of cases, and

$$d = \frac{{date_{last} - date_{first} }}{{date_{end} - date_{start} }}$$

The dates date _first and date _last are the dates of the first and last cases in the scanning window, respectively. Typically a minimum scanning window of 5 is used. Lambda is calculated for every possible subset of n consecutive cases for n = 5,…, r

The lambda for each subset of cases is calculated and the largest found is recorded along with the details of the start and end dates. Next, simulated datasets are generated each with r uniform random numbers in the interval [0,1]. For each simulation, the lambda for each subset is calculated and the largest lambda is recorded. After, for example, 999 iterations the lambdas are ordered by size from smallest to largest and the 95th percentile is noted as λ_sig. If the lambda from the real dataset is greater than to λ_sig then the cases are designated as a significant cluster.

The method assumes a uniform distribution of cases and hence no seasonal variation.

Multiple cases in the observed data can occur on the same day. Where the number of cases in a single day is equal to or greater than the minimum window size, the d value for that window will equal zero and hence lambda will equal infinity. A nominal value equivalent to an hour is added to each case that occurs on the same day, thereby distributing multiple cases. An upper limit of 24 cases within a day is a reasonable assumption in our context. The alternative of distributing same-day cases uniformly across 24 h would, in theory, be preferred.

It should be noted that different statistical terminology was adopted in EUROCAT to avoid confusion with variable names in computer coding. Hence our notation uses ‘r’ in place of ‘N’. To maintain consistency between the code and this article, we have used same terminology in the code and the paper.