A hyperbolic approach for learning communities on graphs

Abstract

Detecting communities on graphs has received significant interest in recent literature. Current state-of-the-art approaches tackle this problem by coupling Euclidean graph embedding with community detection. Considering the success of hyperbolic representations of graph-structured data in the last years, an ongoing challenge is to set up a hyperbolic approach to the community detection problem. The present paper meets this challenge by introducing a Riemannian geometry based framework for learning communities on graphs. The proposed methodology combines graph embedding on hyperbolic spaces with Riemannian K-means or Riemannian mixture models to perform community detection. The usefulness of this framework is illustrated through several experiments on generated community graphs and real-world social networks as well as comparisons with the most powerful baselines. The code implementing hyperbolic community embedding is available online https://www.github.com/tgeral68/HyperbolicGraphAndGMM.

Implementation

The package available at https://github.com/tgeral68/HyperbolicGraphAndGMM (soon to be released to the public) provides python code for performing graph embedding in the Poincaré Ball $\mathbb {B}^m$ for all dimensions $m\le 10$ and to apply Riemannian versions of Expectation-Maximisation (EM) and K-Means algorithm as detailed in the paper. The Readme details the required dependencies to operate the code, how to reproduce the results of the paper as well as effective ways to run experiments (produce a grid search, evaluate performances and so on). The code uses PyTorch backend with 64-bits floating-point precision (set by default) to learn embeddings. In this section, further details of the procedures are presented in addition to those given in the paper and the Readme .

1.1 Centroids initialisation

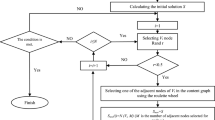
To initialise both the centroids of the K-Means and the means of the Gaussian mixture models, one can use smart initialisations or random ones. A common way to initialise means or centroids is the K-Means++ algorithm using a smart initialisation instead of a purely random one. The main principle relies on selecting centroids that are far away from each other, consequently improving the initialisation. To this end, before running K-Means or Expectation-Maximisation algorithms, the means or centroids are selected as follow:

• 1. For the first iteration, choose the first centroid $c_1$ randomly from the embedded points according to a uniform distribution.

• 2. For a future iteration t, sample a new centroid $c_t$ according to $p(x|c_1, c_2,\ldots ,c_{t-1})$, that associates a low probability for choosing x if it is associated to one of the existing centroids ($\{c_1,\ldots ,c_{t-1}\}$. Technically, the distribution is implemented by finding for each point the closest centroid in $\{c_1, c_2, \dots , c_t\}$ such that $f(x) = \min \limits _{\{c_1, c_2, \dots , c_t\}} d_h(x, c_i)$ then computing for each point $p(x|c_{1}, c_2,\ldots ,c_{t-1}) = \frac{d_h(x, f(x))^2}{\sum \limits _{z \in \mathcal {D}} d_h(z, f(z))^2}$

• 3. Repeat until K centroids have been chosen

The K-Means++ is implemented in the framework as a hyper-parameter of K-Means.

1.2 EM Algorithm

• Weighted Barycentre We set for variable $\lambda$ (learning rate) and $\epsilon$ (convergence rate) in Algorithm 1 of the paper the values $\lambda =5e-2$ and $\epsilon =1e-4$.

• Normalisation coefficient We compute the normalisation factor of the Gaussian distribution for $\sigma$ in the interval [1e-3,2] with step size of 1e-3. This parameter is a quite important since if the minimum value of sigma is too high then unsupervised precision is better on datasets for which it is difficult to separate clusters in small dimensions (Wikipedia, BlogCatalog mainly) as discussed in the previous MCC subsection (In Sect. 4.4.1, the most common community labelled $\approx 47\%$ of the nodes for Wikipedia and $\approx 17\%$ for BlogCatalog).

• EM convergence In the provided implementation, the EM is considered to have converged when the values of $w_{ik}$ change less than 1e-4 w.r.t the previous iteration, more formally when:

  $$\begin{aligned} \frac{1}{N}\sum \limits _{i=0}^N\frac{1}{K}\sum \limits _{k=0}^K(|w_{ik}^t-w_{ik}^{t+1}|)<1e-4 \end{aligned}$$

  For instance, using Flickr the first update of GMM distribution converged in approximately 50 to 100 iterations.

1.3 Learning embeddings

• Optimisation In some cases, due to the Poincaré ball distance formula, the updates of the form $\text {Exp}_u(\eta \nabla _uf(d(u,v))$ can reach a norm of 1 (because of floating point precision). In this special case we do not take into account the current gradient update. If it occurs too frequently, we recommend to lower the learning rate.

• Moving context size Similarly to ComE, we use a moving size window on the context instead of a fixed one; thus we uniformly sample the size of the window between the max size given as input argument and 1.

1.4 Limitations for going in high dimensions

Numerical instabilities when computing the normalisation coefficient $\zeta _m(\sigma )$ in Hyperbolic space. Recall that in Euclidean space, the normalisation coefficient of the multivariate isotropic Gaussian distribution is a linear function of the dimension m: $(2\pi \sigma )^{m/2}$. As for the Poincaré space used in the paper, the expression of the normalisation factor is:

$$\begin{aligned} \zeta _m(\sigma ) = \sqrt{\frac{\pi }{2}}\frac{\sigma }{2^{m-1}} \sum \limits ^{m-1}_{k=0} (-1)^k C^{k}_{m-1} e^{\frac{p_k^2\sigma ^2}{2}}\bigg ( 1+\text {erf}(\frac{ p_k\sigma }{\sqrt{2}})\bigg ) \end{aligned}$$

Fig. 15

Normalisation coefficient (y-axis) $\sigma \mapsto \zeta _m(\sigma )$ of Gaussian distributions on Hyperbolic space for different values of the dimension m (x-axis) and of the variance $\sigma$

Referring to Fig. 15, we can observe that $\zeta _m(\sigma )$ increases exponentially as a function of m. Therefore, when increasing the dimension from 1 to 128 the computed probabilities $f(x|\mu ,\sigma )$ where

$$\begin{aligned} f(x|\mu ,\sigma )=\frac{1}{\zeta _m(\mu ,\sigma )} \exp \left[ -\frac{d^2(x,\mu )}{2\sigma ^2}\right] \end{aligned}$$

become the result of a division with an ever-increasing number causing out-of-bound issues and numerical instabilities. This problem seems to be equally faced by the authors of Mathieu et al. (2019), who adapted variational auto-encoders to the Poincaré space. Their experiments are performed using 20 dimensions at most.

The ComE approach is however capable of reaching high dimensions without dealing with numerical instability issues.

A possible solution to this problem could be to reconsider the mathematical model at higher dimensions, and provide computationally efficient formulas that deals with floating representations. The very recent paper Heuveline et al. (2021) seems to have found new asymptotic formulas of the normalising factor on typical manifolds when the dimension grows and is definitively worth investigating to overcome the current difficulty.