Dynamic Multilayer Network for Systemic Risk and Bank Regulation Based on CDS

Abstract

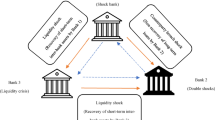
During the U.S. subprime mortgage crisis, credit default swaps (CDS) played a pivotal role and became an influential booster. However, most studies only study the systemic risk of CDS in the interbank market and do not quantify how CDS speculation affects the systemic risk. Therefore, to study the impact of CDS speculation on the systemic risk, this paper constructs a multi-layered complex network, which includes bank-firm-CDS sellers to reproduce speculation in the CDS market. Then, the impact of different CDS speculation ratios and regulatory ratios on the banking systemic risk of a multi-layered complex network are investigated separately under different credit shocks. The results show that the systemic risk is positively correlated with the CDS speculation ratio, and that speculation adversely influences system stability, although it is profitable for some banks. Moreover, the effectiveness of the regulation is affected by the size of credit shocks, if credit shocks are large, the systemic risk is negatively related to regulatory ratios. Because the regulation system on CDS sellers limits the expansion of the CDS market, reduces the counterparty risk for banks, and makes the banking system more stable. Instead, if credit shocks are low, strict regulation has the potential to increase the systemic risk. The study provides a novel perspective on utilizing rational credit risk mitigation instruments to prevent systemic risks.

Appendix: Stability Test and Sensitivity Analysis

1.1 Robustness Test of the Reserve Requirement Ratio $\chi$

This paper constructed a multilayer network model with bank-firm-CDS sellers to study the impact of speculation and regulation on systemic risk in the CDS market, but further tests are needed for the robustness of the multilayer network model. With the development of the financial system, the reserve requirement has gradually evolved into an important monetary policy tool. Considering that the reserve requirement ratio affects the size of banks' credit, which in turn may affect systemic risk under credit shocks. Based on this, this paper varied the reserve requirement ratio ($\chi = \left[ {0.15,0.25} \right]$) while controlling other parameters constant and observed the number of defaults in the three networks, as shown in Table 3 and Fig. 10.

Table 3 Number of defaults for three networks with different reserve requirement ratios

Fig. 10

Number of defaults for three networks with different reserve requirement ratios $\chi$

We found that the number of defaults decreases as $\chi$ increases in the same bank network. This is because the increase in the reserve requirement ratio affects the ability of banks to expand credit, thus reducing credit risk. Although the change in $\chi$ leads to a change in the number of defaults in the network, the conclusion of the paper remains unchanged: speculation in the CDS market increases systemic risk; regulation of the CDS market reduces systemic risk. Therefore, the model results in this paper are robust to changes in the reserve requirement ratio.

1.2 Sensitivity Analysis of Margin Parameter

The amount of margin required from a CDS seller is related to the volatility of the CDS market price. The higher the market price volatility, the higher the margin required from the CDS seller. Therefore, it is necessary to investigate the sensitivity of the market price volatility parameter to the model results. This paper varied the CDS market price volatility ($\sigma_{c} = \left[ {0.01,0.1} \right]$) while controlling other parameters constant and observed the number of defaults in the banking system, as shown in Fig. 11.

In Fig. 11, the number of defaults in the system increases slightly as $\sigma_{c}$ rises. The number of defaults is more sensitive to $\sigma_{c}$ when $\sigma_{c}$ is larger. But overall, the sensitivity of $\sigma_{c}$ is low and has little effect on the simulation results. This indicates that the model in this paper has good stability.

Fig. 11

Number of defaults under different CDS market price volatility $\sigma_{c}$