Towards Energy-Balance Closure with a Model of Dispersive Heat Fluxes

Abstract

In the last decades the energy-balance-closure problem has been thoroughly investigated from different angles, resulting in approaches to reduce but not completely close the surface energy balance gap. Energy transport through secondary circulations has been identified as a major cause of the remaining energy imbalance, as it is not captured by eddy covariance measurements and can only be measured additionally with great effort. Several models have already been developed to close the energy balance gap that account for factors affecting the magnitude of the energy transport by secondary circulations. However, to our knowledge, there is currently no model that accounts for thermal surface heterogeneity and that can predict the transport of both sensible and latent energy. Using a machine-learning approach, we developed a new model of energy transport by secondary circulations based on a large data set of idealized large-eddy simulations covering a wide range of unstable atmospheric conditions and surface-heterogeneity scales. In this paper, we present the development of the model and show first results of the application on more realistic LES data and field measurements from the CHEESEHEAD19 project to get an impression of the performance of the model and how the application can be implemented on field measurements. A strength of the model is that it can be applied without additional measurements and, thus, can retroactively be applied to other eddy covariance measurements to model energy transport through secondary circulations. Our work provides a promising mechanistic energy balance closure approach to 30-min flux measurements.

1 Introduction

The quantification of energy transport between ecosystems and the atmosphere provides an important basis for various areas of environmental science. Some examples are operational weather forecasting and climate modelling (e.g. Arneth et al. 2012; Cuxart et al. 2015; Green et al. 2017), or investigating the reaction of ecosystems to changing climate conditions (e.g. Cremonese et al. 2017; Fu et al. 2020; Qu et al. 2016; Reichstein et al. 2007; van Gorsel et al. 2016) to come up with sustainable management strategies for ecosystems and adapt agriculture (e.g. Bernacchi et al. 2005, 2006; Ceschia et al. 2010; Graham et al. 2016; O’Dell et al. 2020; Stork and Menzel 2016). For decades, the eddy covariance (EC) method has been used to quantify energy transport in the atmospheric boundary layer in terms of sensible and latent heat fluxes at the ecosystem scale, as it facilitates the direct measurement of turbulent energy fluxes without disturbing the investigated ecosystem (Aubinet et al. 2012; Baldocchi 2003, 2014; Foken 2017; Mauder et al. 2007a).

However, the systematic study of measurements at EC stations has shown that the surface-energy balance (SEB, the balance between incoming and outgoing energy at the surface in the form of radiation, heat fluxes and storage change) is usually not closed, but shows a gap of 10–30%, always in the same direction (Hendricks-Franssen et al. 2010; Soltani et al. 2018; Stoy et al. 2013). The SEB can therefore be expressed in simplified form as:

$$ R_{{{\text{net}}}} = H_{t} + \lambda E_{t} + G + I, $$

(1)

where ${R}_{net}$ is the net radiation, which is defined to be positive during daytime, ${H}_{t}$ and ${\lambda E}_{t}$ are the sensible and latent turbulent fluxes measured with the EC method, $G$ is the ground heat flux and $I$ is the remaining SEB gap (Mauder et al. 2020). The terms on the right-hand side of the equation are defined to be positive when they transport energy away from the surface.

The SEB gap has been the subject of research for a long time and many factors, such as systematic errors in the measurement of the vertical wind component and humidity (Frank et al. 2013; Goulden et al. 1996; Kochendorfer et al. 2012; Laubach et al. 1994; Mauder 2013; Nakai and Shimoyama 2012), which are used to calculate heat fluxes, and systematic errors in the measurement of other components of the SEB, such as the radiation and ground heat flux (Foken 2008; Kohsiek et al. 2007; Liebethal et al. 2005), and the scale mismatch between the footprint of the EC measurement and the radiation measurement (Schmid 1997) have been studied. Especially for measurement towers above high vegetation, the energy storage in the air volume and biomass below the measurement instruments also plays a non-negligible role and should be captured by profile measurements of temperature and humidity (Leuning et al. 2012; Lindroth et al. 2010; Moderow et al. 2009; Xu et al. 2019). The influences of systematic measurement errors were minimized or can be accounted for by appropriate measures in the data processing (Mauder et al. 2006; Mauder and Foken 2006; Twine et al. 2000) but a significant gap in the SEB remains (Mauder et al. 2006, 2007c, 2020).

One reason for the remaining SEB gap could be the fact that the EC method, given typical approaches and measurement limitations, only captures turbulent transport: the flux is calculated as the covariance of the vertical wind speed and a scalar of interest (e.g., temperature for the sensible heat flux $H$ or humidity for the latent heat flux $\lambda E$) from high-frequency time series. The covariance is based on the fluctuations around an average over a certain averaging period of typically 30 min (Aubinet et al. 1999; Mauder et al. 2020). The averages of the wind speed and scalar of interest are not considered and any energy transport by structures that contribute to the mean vertical wind speed is neglected (Metzger and Holmes 2007). The temporal or spatial averaging period used to represent the Reynolds’ average defines which atmospheric structures ultimately contribute to “turbulent” and which contribute to “non-turbulent” transport.

After assuming for a long time that energy transport in the atmospheric boundary layer (ABL) is exclusively turbulent in nature, i.e., that all relevant transport is captured by applying 30-min averaging intervals, it has been found that large eddies, also known as secondary circulations (SCs) reach near the surface (Eder et al. 2015; Patton et al. 2016). SCs contribute to the mean wind speed at typical EC averaging periods, which is why the energy transport by SCs is not considered in EC measurements and instead contributes to the SEB gap (Foken 2008; Mauder et al. 2020).

Two main types of SCs can be distinguished. The first type are randomly developing large eddies that are turbulent in nature but so large that they are not considered in the covariance over the averaging period and even form over homogeneous surfaces, so called turbulent organized structures (TOSs) (Inagaki et al. 2006; Kanda et al. 2004). The second type are systematically developing secondary circulations caused by differential heating at the earth surface and therefore bound in space, so called thermally-induced mesoscale circulations (TMCs) (Bou-Zeid et al. 2020; Foken 2008; Kenny et al. 2017; Mauder et al. 2020). Increasing the averaging period might sample more of the energy transported due to the randomly organized and quasi-stationary TOSs with longer time scales as they move slowly with the mean wind within the tower footprint. However, TMCs are spatially bound to surface characteristics which is why they still contribute to the mean wind even with long averaging periods as they might not be sampled by fixed-point EC tower measurements. This may explain why in some cases, increasing the averaging period had no effect on the SEB closure in some cases (Charuchittipan et al. 2014) but improved the SEB closure, though not entirely resolved it, in other cases (Finnigan et al. 2003; Mauder et al. 2006). Furthermore, increasing the averaging period in EC measurements beyond multiple hours will eventually violate the assumption of stationarity (Mauder et al. 2006, 2020). Wavelet-based flux calculation approaches that incorporate longer wavelength turbulent transport have been shown to improve the SEB gap, also implying a role for SCs in energy transport (Metzger et al. 2013; Xu et al. 2020). The SEB gap is therefore to some extent a result of the different scales at which ecosystem-atmosphere interactions take place (Desai et al. 2022b).

The contribution of the transport by secondary circulations can be quantified by spatial measurements using an array of tower measurements or aircraft measurements (Feigenwinter et al. 2008; Mahrt 1998; Mauder et al. 2008; Paleri et al. 2022b; Steinfeld et al. 2007). However, those measurements are expensive and cannot be carried out at each EC station or over long periods. Another possibility is to model the energy transport by secondary circulations based on atmospheric and landscape parameters that can be gathered for single-tower EC measurements (e.g. Choi et al. 2009; De Roo et al. 2018; Eder et al. 2014; Huang et al. 2008; Mauder et al. 2021; Panin and Bernhofer 2008).

Systematic studies at multiple EC sites were carried out that found surface heterogeneity (Foken et al. 2010; Mauder et al. 2007b; Morrison et al. 2021; Panin et al. 1998; Panin and Bernhofer 2008), friction velocity ${u}_{*}$ (Barr et al. 2006; Hendricks-Franssen et al. 2010; Stoy et al. 2013; Wilson et al. 2002), and atmospheric stability (Barr et al. 2006; Hendricks-Franssen et al. 2010; Stoy et al. 2006, 2013) to be related to the SEB gap. The SEB gap was also studied with large-eddy simulations (LES), which also found surface heterogeneity (De Roo and Mauder 2018; Zhou et al. 2019), ${u}_{*}$ (Schalkwijk et al. 2016) and atmospheric stability (Huang et al. 2008; Zhou et al. 2018) were influencing the SEB gap.

That the SEB gap depends on atmospheric stability follows from the fact that convectively driven eddies predominate under unstable conditions. Their vertical extent can reach the ABL depth (Maronga and Raasch 2013; Sühring and Raasch 2013), and their horizontal extent can reach two to three times the boundary layer depth (Paleri et al. 2022a; Stull 1988). These large eddies are not captured in 30-min EC measurements and therefore are considered TOSs. Furthermore, large horizontal wind speeds that are associated with neutral to stable atmospheric conditions increase the horizontal mixing (Katul 2019; Schalkwijk et al. 2016), and TOSs are carried along faster with the wind, increasing the likelihood of them being captured within a typical 30-min measurement period. The thermal surface heterogeneity affects the SEB gap through its influence on the formation of SCs: different surface properties of the individual patches cause the surfaces and also the air above them to heat up to different extents, resulting in the formation of TMCs in addition to the TOSs that are already randomly formed. The magnitude of the TMCs depends on the prevalent size and temperature amplitude of the individual surface patches (Inagaki et al. 2006; Letzel and Raasch 2003; Sühring et al. 2018; Zhou et al. 2019).

Several studies proposed models of the SEB gap based on atmospheric stability and measurement height (e.g. De Roo et al. 2018; Huang et al. 2008). Recently, a model of the SEB gap including the effect of thermal surface heterogeneity was published (Wanner et al. 2022b), however, it was only developed to predict the imbalance in the sensible heat flux. These models all have in common that they model the entire SEB gap, i.e., the gap between the available energy at the surface and the measured turbulent heat fluxes.

However, the energy being stored in the air layer and biomass beneath the instruments were identified as another major contribution to the SEB gap in EC measurements over tall vegetation, as mentioned above. We hypothesize that the amount of energy supplied to this storage does not depend on the same factors as the magnitude of the energy transport by secondary circulations. It is possible to measure the energy storage change in the air by simply adding few sensors below the EC instrumentation (Lindroth et al. 2010; Moderow et al. 2009). This is already implemented by default in some large EC networks like ICOS (Heiskanen et al. 2022) and provides a more direct way of obtaining the storage change contribution to the SEB than predicting it by a model. Since storage change is being routinely measured at EC sites and its effect on the long-term mean SEB is negligible, we propose to measure the storage directly and model the energy transport by secondary circulations separately.

Considering the mentioned contributions to the SEB gap, we can rewrite Eq. 1 as:

$$ R_{net} = H_{t} + \lambda E_{t} + H_{nt} + \lambda E_{nt} + G + H_{\Delta St,a} + \lambda E_{\Delta St,a} + H_{\Delta St,b} + I, $$

(2)

where ${H}_{nt}$ and ${\lambda E}_{nt}$ are non-turbulent transport of sensible and latent heat which is missed by EC the measurement, ${H}_{\Delta St,a}$ and ${\lambda E}_{\Delta St,a}$ are storage changes of sensible heat in the air volume below the EC measurement, and ${H}_{\Delta St,b}$ is the storage change of sensible heat in the biomass. If a small volume surrounding the EC site is considered, the non-turbulent fluxes ${H}_{nt}$ and ${\lambda E}_{nt}$ contribute to horizontal and vertical advection. In an infinite observation area, they contribute to the dispersive fluxes (Raupach and Shaw 1982; Wilson and Shaw 1977), that are calculated as the spatial covariance of 30-min averaged values of $w$ and $\theta$ or $q$. This yields:

$${H}_{d}(z)=\langle {\overline{w} }^{*}{\overline{\theta }}^{*}\rangle (z) {c}_{p}\rho, $$

(3)

for the sensible dispersive heat flux ${H}_{d}$, where ${c}_{p}$ is the specific heat capacity of air and $\rho$ is the air density. The overbar refers to temporal averaging over 30 min and angular brackets denote spatial averaging over the observation area. The upper * refers to spatial fluctuations which are averaged over all grid boxes horizontally. The spatial covariance is therefore defined as:

$$\langle {\overline{w} }^{*}{\overline{\theta }}^{*}\rangle \left(z\right)=\frac{1}{{n}_{x}\cdot {n}_{y}}\sum_{x=0}^{{x}_{max}}\sum_{y=0}^{{y}_{max}}\left(\overline{w }\left(x,y,z\right)-\langle \overline{w }\rangle \left(z\right)\right)\left(\overline{\theta }\left(x,y,z\right)-\langle \overline{\theta }\rangle \left(z\right)\right),$$

(4)

where and ${n}_{x}$ and ${n}_{y}$ refer to the number of grid points in x- and y-direction. The latent dispersive heat flux ${\lambda E}_{d}$ is calculated similarly following:

$${\lambda E}_{d}(z)=\langle {\overline{w} }^{*}{\overline{q} }^{*}\rangle (z) {\lambda }_{v}\rho, $$

(5)

where ${\lambda }_{v}$ is the latent heat of vaporization and:

$$\langle {\overline{w} }^{*}{\overline{q} }^{*}\rangle \left(z\right)=\frac{1}{{n}_{x}\cdot {{n}_{y}}}\sum_{x=0}^{{x}_{max}}\sum_{y=0}^{{y}_{max}}\left(\overline{w }\left(x,y,z\right)-\langle \overline{w }\rangle \left(z\right)\right)\left(\overline{q }\left(x,y,z\right)-\langle \overline{q }\rangle \left(z\right)\right).$$

(6)

By considering ${H}_{nt}$, ${\lambda E}_{nt}$, ${H}_{\Delta St,a}$, ${\lambda E}_{\Delta St,a}$, and ${H}_{\Delta St,b}$ $I$ becomes smaller. Therefore, to close the energy balance gap eventually, all known factors contributing to the energy balance must be quantified.

Since the long-term measurement of non-turbulent fluxes at all EC sites is not possible, the main objective of this study is to develop a model that can predict the transport of sensible and latent heat by SCs under unstable conditions at the site of an EC station based on as few additional measurements as possible. Further objectives are (1) to test how well the model predicts the partitioning into sensible and latent energy transport by secondary circulations in a more realistic LES, and (2) to show how the model can be applied to field measurements and test if considering the modelled dispersive fluxes results in an SEB closure in EC field measurements. The main objective is achieved by further developing an existing model (Wanner et al. 2022b). Following De Roo et al. (2018) it uses the atmospheric stability measure ${u}_{*}/{w}_{*}$, where ${w}_{*}$ is the Deardorff velocity, and the measurement height $z$ normalized with the atmospheric boundary-layer height ${z}_{i}$, as well as a thermal surface heterogeneity parameter $\mathcal{H}$ (Margairaz et al. 2020b) to predict the entire energy balance gap. The new model developed in this study additionally considers the gradients of potential temperature $\theta$ to predict the non-turbulent transport of $H$ and mixing ratio $q$ to predict the non-turbulent transport of $\lambda E$. We hypothesize that the consideration of these gradients improves the prediction of energy transport by SCs since they define whether there is any energy to be transported by secondary circulations. The model is based on a large set of idealized LESs introduced in Sect. 2.1 and also contributes to a better understanding of the partitioning of the SEB gap into sensible and latent heat as well as non-turbulent fluxes and storage change, respectively.

The additional objectives to test the model are addressed by applying the model to more realistic LES (Sect. 2.3, Paleri et al. (2023)) and field measurements at EC stations (Sect. 2.4) from the CHEESEHEAD19 campaign (Butterworth et al. 2021). The application to the more realistic LES allows a separate analysis of the surface balances of sensible and latent heat, which is not possible with field measurements, where only the total available energy can be used as a reference. The test using the field measurements is intended to show how practicable the model application is and how well the findings from the LES can be transferred to the real world.

The development and application of the model are described in Sect. 2. The results are shown in Sect. 3 and discussed in Sect. 4.

2 Methods

2.1 Set-up of Idealized Large-Eddy Simulations

We used PALM V6, revision 4849 to run a set of idealized simulations. PALM is a parallelized LES model based on the non-hydrostatic incompressible Boussinesq equations (Maronga et al. 2020; Raasch and Schröter 2001). The sub-grid model was based on the kinetic energy scheme of Deardorff (1980) which was modified by Moeng and Wyngaard (1988) and Saiki et al. (2000). A fifth-order scheme (Wicker and Skamarock 2002) was used to discretize the advection terms, and for the time integration, a third-order Runge–Kutta scheme (Williamson 1980) was used.

In total, we ran 148 simulations with different combinations of geostrophic wind speeds (${U}_{g}$, 0.5–9.0 m s⁻¹), surface patch sizes of sensible (${H}_{{\text{s}}}$) and latent (${\lambda E}_{{\text{s}}}$) surface fluxes (homogeneous, 200 m, 400 m, 800 m), and Bowen ratios ($\beta$) of surface fluxes (0.1–1.3), following the setup used in Margairaz et al. (2020a) and Wanner et al. (2022b). The randomly assigned surface fluxes followed a Gaussian normal distribution, where the standard deviation was also varied. Table 6 in Appendix 1 gives an overview over the individual simulations. The variation in ${U}_{g}$, ${H}_{{\text{s}}}$, and ${\lambda E}_{{\text{s}}}$ led to differences in atmospheric stability and the variation in heterogeneity scales of surface fluxes caused the development different patterns of surface temperature (${T}_{{\text{s}}}$). Examples of the spatial distribution of surface fluxes and resulting surface temperatures can be found in Fig. 11 (Appendix 1).

Following Margairaz et al. (2020a) and Wanner et al. (2022b), the horizontal grid spacing was 24.5 m and the vertical grid spacing was 7.8 m. With (x,y,z) = 256 × 256 × 256 grid points, this resulted in a horizontal domain extent of 6272 × 6272 m² and a vertical domain extent of roughly 2000 m. All simulations were carried out with cyclic horizontal boundary conditions. At the lower boundary, Dirichlet boundary conditions were used for the wind velocity components, while Monin–Obukhov similarity theory was used to determine the lower boundary condition for the momentum equations, and Neumann boundary conditions were used for potential temperature, humidity, pressure and turbulent kinetic energy. The roughness length was set to 0.1 m, following Margairaz et al. (2020a) and Wanner et al. (2022b).

The initialization profiles were set up following De Roo et al. (2018). The same horizontally homogeneous initial vertical profiles of potential temperature $\theta$ and mixing ratio $q$ were used in all 148 simulations. The surface temperature was horizontally homogeneous and set to 285 K. A vertical gradient of 3·10⁻³ K m⁻¹ was applied between 40 and 800 m and a vertical gradient of 8·10⁻³ K m⁻¹ was applied between 800 and 1000 m, ensuring that the top of the domain lay within an inversion layer and the atmospheric processes in the boundary layer were not affected by the upper border of the domain. The humidity was set to 1·10⁻³ kg kg⁻¹ at the surface and only between 1000 and 1100 m, a vertical gradient of − 1·10⁻⁵ kg kg⁻¹ m⁻¹ was applied.

The initial profile of horizontal wind speed was horizontally and vertically constant. The wind speed varied among the simulations between 0.5–9.0 m s⁻¹ (Table 6, Appendix 1) and generated a horizontal pressure gradient in x-direction. A small vertical pressure gradient to counteract excessive boundary-layer growth was introduced by a vertical subsidence velocity gradient (− 4·10⁻⁵ s⁻¹ between 0 and 800 m and − 2·10⁻⁵ s⁻¹ between 8 and 1000 m).

After a 4-h spin-up period, the output data was collected for a 30-min averaging period representing typical EC averaging periods (Rebmann et al. 2012). The profiles of temperature, humidity, and horizontal wind speed during the data collection period is shown as an example for two simulations in Fig. 12, Appendix 1.

2.2 Development of the Dispersive Flux Model

2.2.1 Data Processing

Following the approach of former models, we developed a model using horizontally domain-averaged values from an idealized set of LESs. Since the idealized LESs had cyclic horizontal boundary conditions, the horizontal and vertical advection fluxes (${H}_{a}$, ${\lambda E}_{a}$) became zero on the ecosystem scale and all energy transport by secondary circulations was combined in the dispersive fluxes. Therefore, the horizontally averaged total available energy at the surface, i.e., the heat fluxes originating from the surface ($\langle {H}_{{\text{s}}}\rangle$, $\langle {\lambda E}_{{\text{s}}}\rangle$), was divided into horizontally averaged non-organized randomly distributed turbulent fluxes ($\langle {H}_{t}\rangle$, $\langle {\lambda E}_{t}\rangle$), including the sub-grid-scale contributions ($\langle {H}_{{\text{sgs}}}\rangle$, $\langle {\lambda E}_{{\text{sgs}}}\rangle$), dispersive fluxes (${H}_{d}$, ${\lambda E}_{d}$), and horizontally averaged storage change of energy in the underlying air mass ($\langle {H}_{\Delta St}\rangle$, $\langle {\lambda E}_{\Delta St}\rangle$) as follows:

$$\langle {H}_{{\text{s}}}\rangle +\langle {\lambda E}_{{\text{s}}}\rangle =\langle {H}_{t}\rangle +\langle {\lambda E}_{t}\rangle +{H}_{d}+{\lambda E}_{d}+\langle {H}_{\Delta St}\rangle +\langle {\lambda E}_{\Delta St}\rangle +{H}_{a}+{\lambda E}_{a},$$

(7)

with ${H}_{a}={\lambda E}_{a}=0$ W m⁻¹.

The 30-min horizontally averaged turbulent sensible heat flux $\langle {H}_{t}\rangle$ was calculated for each grid level up to $z/{z}_{i}= 0.1$ using the 30-min averaged vertical wind speed $w$ and potential temperature $\theta$, the 30-min averaged temporal covariance of $w$ and $\theta$, and the sub-grid-scale contribution ${H}_{{\text{sgs}}}$, following:

$$\langle {H}_{t}\rangle \left(z\right)= \langle \overline{w\theta }\left(z\right)-\overline{w }\left(z\right) \overline{\theta }\left(z\right)\rangle {c}_{p}\rho +\langle {H}_{{\text{sgs}}}\rangle .$$

(8)

The horizontal averaging was performed over the entire extent of the domain. The same procedure was used to calculate the horizontally averaged 30-min turbulent latent heat flux $\langle {\lambda E}_{t}\rangle$, however, instead of $\theta$, the mixing ratio $q$ was used:

$$\langle {\lambda E}_{t}\rangle \left(z\right)= \langle \overline{wq }\left(z\right)-\overline{w }\left(z\right) \overline{q }\left(z\right)\rangle {\lambda }_{v}\rho +\langle {\lambda E}_{{\text{sgs}}}\rangle .$$

(9)

The dispersive sensible and latent heat fluxes ${H}_{d}$ and ${\lambda E}_{d}$ were calculated over the entire horizontal extent of the domain following Eqs. 3–6. Equations 3 and 5 show that ${H}_{d}$ and ${\lambda E}_{d}$ were by definition already horizontally averaged.

Since the LESs had cyclic boundary conditions and any other flux contributions could be ruled out, the change of energy stored in the underlying air mass (${H}_{\Delta St}$, ${\lambda E}_{\Delta St}$) was calculated as the residual of the other contributions to the total available surface flux:

$$\langle {H}_{\Delta St}\rangle =\langle {H}_{{\text{s}}}\rangle -\langle {H}_{t}\rangle -{H}_{d},$$

(10)

and:

$$\langle {\lambda E}_{\Delta St}\rangle =\langle {\lambda E}_{{\text{s}}}\rangle -\langle {\lambda E}_{t}\rangle -{\lambda E}_{d}.$$

(11)

To model ${H}_{d}$ and ${\lambda E}_{d}$, we proposed variables of atmospheric stability $\langle {u}_{*}/{w}_{*}\rangle$, the thermal heterogeneity parameter $\mathcal{H}$, the measurement height ${z}_{m}$ normalized with the atmospheric boundary layer height $\langle \overline{{z }_{i}}\rangle$, and the vertical differences of potential temperature theta $\langle \Delta \overline{\theta }\rangle$ (for ${H}_{d}$) and mixing ratio $\langle \Delta \overline{q }\rangle$ (for ${\lambda E}_{d}$), respectively, as our driving factors.

We calculated $\langle {u}_{*}/{w}_{*}\rangle$, for one grid level near the surface based on the 30-min averaged covariances following:

$${u}_{*}={\left({({\overline{{u }{\prime}{w}{\prime}}}_{{\text{res}}}+\langle {\overline{{u }{\prime}{w}{\prime}}}_{{\text{sgs}}}\rangle )}^{2}+{({\overline{{v }{\prime}{w}{\prime}}}_{{\text{res}}}+\langle {\overline{{v }{\prime}{w}{\prime}}}_{{\text{sgs}}}\rangle )}^{2}\right)}^{1/4},$$

(12)

where $u$ and $v$ are the horizontal wind speeds in x- and y-direction, and the index ${\text{res}}$ indicates the covariance resolved by the grid, and:

$${w}_{*}={\left(\frac{g}{\overline{\theta }}\langle {z}_{i}\rangle ({\overline{{w }{\prime}{\theta }{\prime}}}_{{\text{res}}}+\langle {\overline{{w }{\prime}{\theta }{\prime}}}_{{\text{sgs}}}\rangle \right)}^{1/3},$$

(13)

where $g$ is the gravitational acceleration (9,81 m s⁻²) and ${z}_{i}$ was determined as the height at which the total sensible heat flux crossed the zero value prior to reaching the capping inversion.

The thermal heterogeneity parameter was introduced by Margairaz et al. (2020b) as:

$$\mathcal{H}=\frac{g \overline{{L }_{h}}}{{\langle \overline{{U }_{g}}\rangle }^{2}}\frac{\Delta \overline{T} }{\langle \overline{{T }_{{\text{s}}}}\rangle },$$

(14)

where $\langle \overline{{T }_{{\text{s}}}}\rangle$ is the averaged surface temperature, $\Delta \overline{T }$ is the amplitude of the surface temperature heterogeneities, calculated following:

$$\Delta \overline{T }=\langle \left|\overline{{T }_{{\text{s}}}}-\langle \overline{{T }_{{\text{s}}}}\rangle \right|\rangle ,$$

(15)

and $\langle \overline{{U }_{g}}\rangle$ is the prescribed geostrophic wind speed. The heterogeneity length scale $\overline{{L }_{h}}$ was calculated following an approach of Panin and Bernhofer (2008). We calculated the spatial spectra of $\overline{{T }_{{\text{s}}}}$ by performing a Fourier transformation along ten transects in the x- and y-direction of the domain, respectively. Before performing the Fourier transformation, a bell taper was applied to smooth the edges and thereby reduce leakage (Stull 1988). The length scale that contributed the most to the variability in $\overline{{T }_{{\text{s}}}}$ along each transect was identified as the location of the maximum of the spectrum. By averaging over the predominant length scales derived from each transect along both directions, we derived the predominant length scale $\overline{{L }_{h}}$ of the entire domain.

The vertical differences $\langle \Delta \overline{\theta }\rangle$ and $\langle \Delta \overline{q }\rangle$ were calculated following:

$$\langle \Delta \overline{\theta }\rangle = \langle \overline{\theta }\rangle \left(0 m\right)-\langle \overline{\theta }\rangle \left({0.5 z}_{i}\right),$$

(16)

and:

$$\langle \Delta \overline{q }\rangle = \langle \overline{q }\rangle \left(0 m\right)-\langle \overline{q }\rangle \left({0.5 z}_{i}\right).$$

(17)

2.2.2 Model Fitting

We used the Random Forest machine-learning method (Breiman 2001) to predict ${H}_{d}$ and ${\lambda E}_{d}$ from 148 idealized LESs that were set up to represent a wide range of boundary conditions with respect to thermal surface heterogeneity and atmospheric stability (Sect. 2.1). The models were trained separately for ${H}_{d}$ and ${\lambda E}_{d}$ using $\langle {u}_{*}/{w}_{*}\rangle$, $z/\langle {z}_{i}\rangle$, $\mathcal{H}$, and $\langle \Delta \overline{\theta }\rangle$ (only for ${H}_{d}$) or $\langle \Delta \overline{q }\rangle$ (only for ${\lambda E}_{d}$) as predictor variables. The entire training data is attached as a supplementary file. The modelling was performed in Python 3.7 using the Random Forest implementation in scikit-learn (Pedregosa et al. 2012) with default settings and 200 regression tree estimators.

The random choice of samples in the Random Forest algorithm causes the results to slightly vary. We therefore repeated the model fitting 100 times. To evaluate the approach, we used a leave-one-out-cross-validation such that predictors for ${H}_{d}$ and ${\lambda E}_{d}$ for each simulation have never seen the specific simulation results during training. We calculated predictor importance based on so called SHapley Additive exPlanations (SHAP) values (Lundberg et al. 2020; Lundberg and Lee 2017) which estimate how much each predictor contributes to the variation of the predictions. We used the mean absolute SHAP value for each predictor as a metric of variable importance.

2.3 Testing the Model on the More Realistic CHEESEHEAD19 LES

To test how well the model of sensible and latent dispersive heat fluxes works, we applied from the model of dispersive heat fluxes to the realistic LESs of two days in August (22–23 Aug 2019) of the CHEESEHEAD19 campaign (Paleri et al. (2023) for which we performed eight ensemble simulations. These simulations were carried out with PALM v6, revision 21.10-rc.2 and consisted of one parent domain and two 3D child domains, nested recursively within each other.

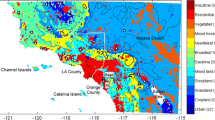
The extent and resolution of the domains is shown in Table 1. The parent domain had a large extent to ensure that turbulence can properly develop and adapt to the surface conditions. The first child domain (C1) covered the surroundings of the CHEESEHEAD19 area with a moderate resolution. The smallest child domain (C2) had a very high resolution to enable the investigation at field-measurement heights and covered the locations of the EC stations that were deployed during the CHEESEHEAD19 campaign. The child domains are shown in Fig. 1.

Table 1 Grid resolution and domain extents for the realistic CHEESEHEAD LES

Fig. 1

The map shows landcover types extracted from the WISCLAND 2.0 dataset (Wisconsin Department of Natural Resources 2016) that was used to inform the CHEESEHEAD LES (Sect. 2.3). The extent of the map corresponds to the C1 domain and the white square shows the border of the C2 domain in the CHEESEHEAD LES. The domains are centred around the WLEF Tall Tower (45.9459°N, 90.2723°W). The orange points represent the EC stations in the field (Sect. 2.4)

The realistic simulations were carried out with lateral and top boundary conditions informed by the National Centers for Environmental Prediction (NCEP) High Resolution Rapid Refresh data assimilation product (Horel and Blaylock 2017) over the study domain and coupled to a land-surface model (LSM) and plant-canopy model (PCM) informed by field-campaign observations and the WISCLAND2 dataset (Wisconsin Department of Natural Resources 2016). Paleri et al. (2023) gave a detailed description of the model setup and comparisons with field measurements.

For this analysis, only 30-min observations with $\langle {H}_{{\text{s}}}\rangle$ ≥ 10 W m⁻² were considered to ensure the model was only applied to unstable conditions. Because some values were not included in the data output at the transition between the individual runs that belong to one simulation, five 30-min intervals had to be discarded, additionally. This resulted in 14 time steps that were used in the analysis. $\langle \overline{{U }_{g}}\rangle$ was extracted as the horizontal wind speed at 1.1 $\langle \overline{{z }_{i}}\rangle$ in the C1 domain. The predominant landcover types in the C2 domain are forests, resulting in a domain-averaged canopy height of $\langle {z}_{{\text{c}}}\rangle$ = 22.08 m and a displacement height of $\langle {z}_{{\text{d}}}\rangle$ = 15.46 m. We considered different measurement heights ${z}_{{\text{m}}}$ up to 60 m above ${z}_{{\text{c}}}$ but periods for which $z/\langle \overline{{z }_{i}}\rangle$ > 0.1 where discarded because the model was developed to predict dispersive fluxes in the inertial surface layer, only. When calculating $z/\langle \overline{{z }_{i}}\rangle$, the displacement height $\langle {z}_{d}\rangle$ was taken into account, with $z = {z}_{{\text{m}}}-\langle {z}_{{\text{d}}}\rangle$ and $\langle \overline{{z }_{i}}\rangle ={\langle \overline{{z }_{i}}\rangle }_{0}-\langle {z}_{d}\rangle$, where ${\langle \overline{{z }_{i}}\rangle }_{0}$ refers to the boundary-layer height relative to the bottom of the domain.

Since the active surface is not located at the lower boundary of the domain in areas with high vegetation, we defined the surface in the realistic simulations to be located at the canopy top level in all areas where the PCM was used, and at the lower boundary of the domain in all areas where no PCM was used. This definition of surface is used for $\langle {u}_{*}/{w}_{*}\rangle$ and ${\overline{T} }_{{\text{s}}}$, and the surface fluxes.

Again, $\langle {u}_{*}/{w}_{*}\rangle$ was calculated following Eqs. 12–13 and averaged over the entire horizontal extent of the C2 domain. The surface temperature was extracted from the true surface temperature output in all non-forested areas where only the LSM but not the PCM was deployed. In the forested areas, ${\overline{T} }_{{\text{s}}}$ was extracted from the tree-dimensional output of potential air temperature at the top of the canopy, assuming that the leaf surface temperature equals the air temperature. Based on this combined surface temperature map, $\Delta \overline{T }$, $\langle {\overline{T} }_{{\text{s}}}\rangle$ and $\overline{{L }_{h}}$ were calculated over a 12.5 × 12.5 km² model extent. $\mathcal{H}$ was calculated for the entire horizontal extent of the C2 domain.

To calculate the vertical gradients $\langle \Delta \overline{\theta }\rangle$ and $\langle \Delta \overline{q }\rangle$, $\langle \overline{\theta }\rangle$ and $\langle \overline{q }\rangle$ were extracted from the C1 output at 0.5 $\langle \overline{{z }_{i}}\rangle$ and at the second grid layer. The C1 domain was used to calculate the vertical gradients because the vertical extent of the C2 domain was too small to include 0.5 $\langle \overline{{z }_{i}}\rangle$ under strongly unstable conditions. $\langle \Delta \overline{\theta }\rangle$ and $\langle \Delta \overline{q }\rangle$ where then calculated following Eqs.16–17.

Since the models of sensible and latent dispersive heat fluxes cannot be extrapolated, they provide unreliable values for measurements for which the predictors lay outside the range of training data. Therefore, all 30-min intervals where one of the predictors lies outside the range of model training data where discarded.

To compare the true dispersive heat fluxes to the predicted dispersive heat fluxes, we estimated the true dispersive heat fluxes by calculating ${H}_{d,{\text{LES}}}$ and ${\lambda E}_{d,{\text{LES}}}$ as spatial covariances of $\overline{w }$, $\overline{\theta },$ and $\overline{q }$ over the entire horizontal extent of the C2 domain for each measurement level following Eqs. 3–6.

2.4 Testing the Model on CHEESEHEAD19 Field Measurements

To test the model on real field measurements, the model was furthermore applied to the eddy-covariance measurements at 16 of the 17 stations from the CHEESEHEAD19 campaign. Station NW4 was excluded from the analysis because it was expected to be strongly influenced by topography due to its location on a steep lake shore, rendering it unsuitable for this analysis as topography effects were not considered in the model of dispersive fluxes. The campaign took place from late June until early October 2019 on a 10 × 10 km² area surrounding the nearly 400 m tall AmeriFlux tower US-PFa located in northern Wisconsin, USA (45.9459°N, 90.2723°W) (Desai et al. 2022a). The tower is surrounded by a nearly flat landscape that was mainly covered by a mix of deciduous and coniferous forests, swamplands, and waterbodies. The locations of the 16 eddy-covariance stations are shown in Fig. 1 and the respective measurement heights and landcover characteristics are shown in Table 2. A detailed description of the measurement campaign, including additional measurements can be found in Butterworth et al. (2021).

Table 2 Overview of the 16 CHEESEHEAD19 EC stations used for testing the application of the model on field measurements, including canopy heights (${z}_{c,{\text{field}}}$), measurement heights (${z}_{m,{\text{field}}}$), displacement heights (${z}_{d,{\text{field}}}$), and vegetation types (VT)

Fluxes of sensible (${H}_{t}$) and latent heat (${\lambda E}_{t}$) were calculated for 30-min intervals using detrended 20 Hz measurements of temperature, water vapor, and vertical wind speed. For the ${H}_{t}$ calculation, the dry air temperature was calculated from the sonic temperature after correction for the effect of water vapor on the speed of sound (Schotanus et al. 1983). For the ${\lambda E}_{t}$ calculation, the water vapor measurements were corrected for density effects (Webb et al. 1980). Vertical wind speed was extracted from the raw 3-dimensional wind vector after a double rotation coordinate transformation.

For this analysis, only 30-min observations with ${H}_{t}$ ≥ 10 W m⁻² and ${R}_{net}$ > 0 W m⁻² were considered to ensure the model was only applied to unstable conditions. For quality assurance, observations with unrealistically high turbulent heat fluxes of (${H}_{t}+{\lambda E}_{t}$) > 1.5 ${R}_{net}$ and observations with (${H}_{t}+{\lambda E}_{t}+{H}_{\Delta St}+{\lambda E}_{\Delta St}$) < 0.5 (${R}_{net}-G$) were discarded. While the latter case would be physically possible, it would result in the SEB gap being larger than the sum of the measured atmospheric heat fluxes and storage changes. In this case, the uncertainty would be so high that the data should be rejected rather than corrected.

To apply the model to field measurements, additional information was needed, as single-tower measurements do not provide information on boundary-layer height, geostrophic wind speed, thermal surface heterogeneity or vertical gradients of potential temperature and mixing ratio. The CHEESEHEAD19 dataset provided a unique opportunity to test this model, because it provided a lot of the needed additional information. However, to show that the application to other eddy-covariance measurements is possible, as well, we used no additional information acquired during the CHEESEHEAD19 campaign and only utilized the dense tower network as a test bed for the dispersive flux model in field settings. Instead, ERA5 reanalysis data and satellite-based land-surface temperature maps were used to inform the dispersive flux model.

The differences of $\overline{\theta }$ and $\overline{q }$, $\overline{{z }_{i}}$ and $\overline{{U }_{g}}$ used to calculate $\mathcal{H}$ were extracted from the hourly ERA5 reanalysis data (Hersbach et al. 2023a, b). $\overline{{z }_{i}}$ was directly extracted from the single-level reanalysis data (Hersbach et al. 2023b). To derive $\overline{{U }_{g}}$, the horizontal wind speed at pressure levels (Hersbach et al. 2023a) was calculated from the $\overline{u }$- and $\overline{v }$-component of the wind vector at each pressure level. The height above ground of each pressure level was derived using the barometric formula. Finally, $\overline{{U }_{g}}$ was derived as the wind speed at 1.1 times the boundary layer top by linearly interpolating between the adjacent model output levels. To calculate $\Delta \overline{\theta }$ and $\Delta \overline{q }$, $\overline{\theta }$ and $\overline{q }$ were derived from the pressure level output and the single level output. At 0.5 $\overline{{z }_{i}}$, $\overline{\theta }$ was calculated from the absolute air temperature and the pressure and $\overline{q }$ was calculated from the specific humidity provided by the pressure level output. Again, linear interpolation was applied to derive theta and q at 0.5 $\overline{{z }_{i}}$. For the near-surface value, we used the 2 m dewpoint temperature and absolute air temperature, as well as the surface pressure provided by the single-layer ERA5 output to calculate $\overline{\theta }$ and $\overline{q }$. The vertical differences were then calculated as $\Delta \overline{\theta }= \overline{\theta }\left(2m\right)-\overline{\theta }(0.5\overline{{z }_{i}})$ and $\Delta \overline{q }= \overline{q }\left(2m\right)-\overline{q }(0.5\overline{{z }_{i}})$, respectively.

Even though $\langle {u}_{*}/{w}_{*}\rangle$ could be calculated from the high-frequency data provided by eddy-covariance measurements, it would not necessarily representative of a larger area surrounding the measurement. Furthermore, $\langle {u}_{*}/{w}_{*}\rangle$ are defined as near-surface values making the calculation of $\langle {u}_{*}/{w}_{*}\rangle$ from measurements at roughly 30 m above the ground not ideal. Therefore, $\langle {u}_{*}/{w}_{*}\rangle$ was also extracted from the ERA5 reanalysis data. While ${u}_{*}$ could be directly extracted from the ERA5 reanalysis data, ${w}_{*}$ was calculated from ${H}_{{\text{s}}}$, $\overline{{z }_{i}}$, 2 m air temperature and surface pressure provided in the ERA5 single-level output following Eq. 13.

To calculate $\mathcal{H}$, $\overline{{L }_{h}}$ as well as $\Delta \overline{T }$ were needed, which were not available from the ERA5 reanalysis data. Therefore, surface temperature maps with a 50 m spatial resolution and 1 h temporal resolution generated from satellite data (Desai et al. 2021) were used to calculate $\overline{{L }_{h}}$, $\langle {\overline{T} }_{{\text{s}}}\rangle$, and $\Delta \overline{T }$. For each EC station, we selected a 10 × 10 km² area surrounding the tower location and then followed the approach of Panin and Bernhofer (2008) described in Sect. 3.2 to derive $\overline{{L }_{h}}$. $\Delta \overline{T }$ and $\langle {\overline{T} }_{{\text{s}}}\rangle$ were also calculated from the same map extents. Since the land-surface temperature maps had a temporal resolution of 60 min, the resulting $\overline{{L }_{h}}$, $\langle {\overline{T} }_{{\text{s}}}\rangle$, and $\Delta \overline{T }$ were linearly interpolated to 30-min values.

3 Results

3.1 Model Based on Domain-Averaged Values

The final model uses the output of all 148 idealized LESs as training data, which is attached as a supplementary file, together with an example dataset and a Python code to apply the model. To make the predicted flows more robust, we suggest repeating the prediction 100 times and averaging the results. Figure 2 shows the results of the cross-validation of the models for sensible and latent dispersive heat fluxes (top) and the relative importance of predicting variables in the models of dispersive heat fluxes. There is a strong correlation between the modelled sensible dispersive heat flux ${H}_{d,{\text{predicted}}}$ and the true dispersive sensible heat flux ${H}_{d,{\text{LES}}}$, with a squared Pearson's correlation coefficient of R² = 0.95. For the latent heat flux, the agreement between modelled (${\lambda E}_{d,{\text{predicted}}}$) and true (${\lambda E}_{d,{\text{LES}}}$) dispersive fluxes is weaker, with R² = 0.75.

Fig. 2

Performance of the model. Top panels show comparisons of modelled dispersive heat fluxes (y-axis) versus true dispersive heat fluxes calculated directly from the LES output (x-axis) for sensible (left) and latent (right) dispersive heat fluxes. Bottom panels show the relative importance of predicting variables in the models of sensible dispersive heat flux (left) and latent dispersive heat flux (right)

The most important predicting variables for ${H}_{d,{\text{predicted}}}$ are the heterogeneity parameter $\mathcal{H}$ and the atmospheric stability parameter $\langle {u}_{*}/{w}_{*}\rangle$. The normalized measurement height $z/\langle \overline{{z }_{i}}\rangle$ and the vertical gradient of potential temperature $\langle \overline{\Delta \theta }\rangle$ are less important but not negligible.

For ${\lambda E}_{d,{\text{predicted}}}$, the most important predicting variable is, again, the heterogeneity parameter $\mathcal{H}$. However, the importance of the atmospheric stability parameter $\langle {u}_{*}/{w}_{*}\rangle$ is much lower. The importance of the normalized measurement height $z/\langle \overline{{z }_{i}}\rangle$ and the vertical difference of mixing ratio $\langle \overline{\Delta q }\rangle$ in predicting ${\lambda E}_{d,{\text{predicted}}}$ compared to $\mathcal{H}$ is, again, lower but not negligible.

Figure 3 shows the relative contribution of the domain-averaged storage and the predicted dispersive fluxes to the SEB gap. The gap between the surface fluxes, i.e., the total available energy, and the turbulent fluxes is on average 15.0 ± 6.4% of $\langle {H}_{{\text{s}}}\rangle$ and 9.6 ± 4.9% of $\langle {\lambda E}_{{\text{s}}}\rangle$. The errors are calculated as the standard deviation across all idealized simulations.

Fig. 3

Relative contributions of the domain-averaged storage and dispersive fluxes predicted by the model based on domain-averaged values to the gaps in sensible and latent heat fluxes. The error bars show the standard deviation of the sums shown in each bar

With 7.7 ± 3.3% of $\langle {H}_{{\text{s}}}\rangle$, $\langle {H}_{\Delta St}\rangle$ contributes to more than 50% to the gap in the sensible heat fluxes. The contribution of ${H}_{d,{\text{predicted}}}$ is slightly smaller with 7.3 ± 4.4% of $\langle {H}_{{\text{s}}}\rangle$. The errors were calculated as the standard deviation across all idealized simulations. $\langle {H}_{t}\rangle$, $\langle {H}_{\Delta St}\rangle$ and ${H}_{d,{\text{predicted}}}$ sum up to 100.0 ± 1.3% of $\langle {H}_{{\text{s}}}\rangle$, indicating that the application of the model leads to a good closure of the gap in the sensible heat flux and the inclusion of the predicted dispersive heat flux leads to a significant reduction of the scatter.

In the latent heat flux, the partitioning between $\langle {\lambda E}_{\Delta St}\rangle$ and ${\lambda E}_{d,{\text{predicted}}}$ is different. $\langle {\lambda E}_{\Delta St}\rangle$ has a smaller share in the flux gap (2.3 ± 1.2% of$\langle {\lambda E}_{{\text{s}}}\rangle$) than the predicted dispersive flux (8.0 ± 6.5% of$\langle {\lambda E}_{{\text{s}}}\rangle$). Thus, the dispersive flux share of the surface flux is larger in the latent heat flux than in the sensible heat flux, although the total gap is smaller in the latent heat flux compared to the sensible heat flux. In sum,$\langle {\lambda E}_{t}\rangle$, $\langle {\lambda E}_{\Delta St}\rangle$ and ${\lambda E}_{d,{\text{predicted}}}$ equal 100.7 ± 5.1% of $\langle {\lambda E}_{\Delta St}\rangle$, resulting in a good closure of the gap in the latent heat fluxes on average. However, the addition of ${\lambda E}_{d,{\text{predicted}}}$ does not cause a reduction of the scatter.

Table 3 shows that the Bowen ratio ($\beta$), i.e., the partitioning between sensible and latent heat, is smaller in the turbulent flux compared to the surface flux. The Bowen ratio of the true dispersive flux $\beta ({F}_{d,{\text{LES}}})$ calculated directly from the LES output is larger than the Bowen ratio of turbulent heat fluxes $\beta (\langle {F}_{t}\rangle )$. The Bowen ratio of the storage change $\beta (\langle {F}_{\Delta St}\rangle )$ is much larger than the Bowen ratio of the other fluxes.

Table 3 Absolute values of the flux contributions and Bowen ratios ($\beta$) show the different partitioning into sensible and latent heat in the surface fluxes ($\langle {F}_{{\text{s}}}\rangle$), turbulent fluxes ($\langle {F}_{t}\rangle$), change in energy storage ($\langle {F}_{\Delta St}\rangle$), as well as true (${F}_{d,{\text{LES}}}$) and predicted (${F}_{d,{\text{predicted}}}$) dispersive heat fluxes

3.2 Model Application to More Realistic CHEESEHEAD19 LES

To test the performance of the model based on domain-averaged values on more realistic scenarios, it was applied to the simulations of two days of the CHEESEHEAD19 campaign.

Figure 4 shows the behaviour of predictor variables over the remaining 30-min intervals of the two days simulation time. The majority of predictor variables encountered in the CHEESEHEAD19 LES lies within the range of predictor variables from the idealized LES that were used to train the model. 18% of the available data had to be discarded, mostly due to small $z/\langle \overline{{z }_{i}}\rangle$ as shown in Fig. 4.

Fig. 4

Time series of the predicting variables ($\langle {u}_{*}/{w}_{*}\rangle$, $\mathcal{H}$, $z/\langle \overline{{z }_{i}}\rangle$, $\langle \overline{\Delta \theta }\rangle$, $\langle \overline{\Delta q }\rangle$) that were encountered in the CHEESEHEAD simulations. The grey shaded areas represent night times and time periods with $\langle {H}_{{\text{s}}}\rangle$ ≥ 10 W m⁻² that were discarded as the model of dispersive fluxes was developed for convective atmospheric conditions only. Some time periods were discarded because the variables needed to calculate ${u}_{*}$ were not output for the time steps in which a new restart run was started. The red shaded areas lie outside the limits of the predictor variables used for training the model. Since most predictor variables refer to a specific level, they are the same for any height considered and therefore shown in grey. Only $z/\langle \overline{{z }_{i}}\rangle$ varies with height. In $z$ and in ${z}_{i}$, the displacement height (15.47 m) is considered. The y-axes are restricted to improve the display of the relevant areas

Figure 5 shows the comparison of the modelled dispersive heat fluxes (${H}_{d,{\text{mod}}}$ and ${\lambda E}_{d,{\text{mod}}}$) with the dispersive heat fluxes directly calculated from the LES output (${H}_{d,{\text{LES}}}$ and ${\lambda E}_{d,{\text{LES}}}$). The model clearly overestimates ${H}_{d,{\text{LES}}}$ by 17.4% on average and slightly overestimates ${\lambda E}_{d,{\text{LES}}}$ by 4.9%. Table 4 shows that in the CHEESEHEAD19 LES, the Bowen ratios of the surface $\beta (\langle {F}_{{\text{s}}}\rangle )$ and turbulent $\beta (\langle {F}_{t}\rangle )$ heat fluxes are nearly similar whereas the Bowen ratio in the dispersive heat fluxes $\beta (\langle {F}_{d,{\text{LES}}}\rangle )$ is considerably lower. The stronger overestimation of ${H}_{d}$ leads to a higher Bowen ratio in the modelled dispersive heat fluxes $\beta (\langle {F}_{d,{\text{mod}}}\rangle )$ compared to $\beta (\langle {F}_{d,{\text{LES}}}\rangle )$, which is closer to $\beta (\langle {F}_{{\text{s}}}\rangle )$ and $(\langle {F}_{t}\rangle )$. The sum of the modelled sensible and latent dispersive heat fluxes overestimates the sum of sensible and latent heat fluxes directly calculated from the LES output by 8.5% which is shown in Fig. 6.

Fig. 5

Comparison of modelled sensible (left) and latent (right) dispersive heat fluxes with the sensible and latent dispersive heat fluxes ${H}_{d,{\text{LES}}}$ and ${\lambda E}_{d,{\text{LES}}}$ calculated as spatial covariances from the output of the more realistic CHEESEHEAD19 LES. The different symbols represent 30-min observation periods used for this analysis and the different colours represent the height above the displacement height. The black lines show an orthogonal distance regression (ODR) forced through the origin, with the solid line representing the ODR with the mean values of the 100 predictions, and the dotted lines representing the standard deviation of ODRs with each of the 100 predictions. The y-values of the markers show the dispersive fluxes averaged over the 100 predictions

Table 4 Bowen ratios ($\beta$) show the different partitioning into sensible and latent heat in the domain-averaged surface fluxes ($\langle {F}_{{\text{s}}}\rangle$), turbulent heat fluxes ($\langle {F}_{t}\rangle$), and true $({F}_{d,{\text{LES}}}$) dispersive heat fluxes directly calculated from the LES output, as well as modelled (${F}_{d,{\text{mod}}}$) dispersive heat fluxes

Fig. 6

Comparison of modelled total dispersive heat fluxes with total dispersive fluxes calculated as spatial covariances from the output of the more realistic CHEESEHEAD19 LES. The different symbols represent 30-min observation periods used for this analysis and the different colours represent the height above the displacement height. The black lines show an orthogonal distance regression (ODR) forced through the origin, with the solid line representing the ODR with the mean values of the 100 predictions, and the dotted lines representing the standard deviation of ODRs with each of the 100 predictions. The y-values of the markers show the dispersive fluxes averaged over the 100 predictions

3.3 Model Application to CHEESEHEAD Field Measurements

The model was also tested on the CHEESEHEAD19 field measurements carried out at 16 EC stations over a period of roughly three months.

Figure 7 shows that not all conditions encountered in the field measurements were represented in the training dataset from the idealized LES. While $\mathcal{H}$ values observed in the CHEESEHEAD19 surface temperature maps are covered quite well by the training data, the range of $\langle {u}_{*}/{w}_{*}\rangle$ and also $\langle \overline{\Delta q }\rangle$ is wider in the field measurements compared to the idealized LES. Again, smaller $z/\langle \overline{{z }_{i}}\rangle$ values occur in the field data due to larger $\langle \overline{{z }_{i}}\rangle$ values in the ERA5 reanalysis data and lower measurement heights in the field. The vertical differences of $\langle \overline{\theta }\rangle$ observed in the ERA5 reanalysis data were typically much larger than the values used to train the model. The percentage of CHEESEHEAD19 predictor variables that fall into the limits of the training data for each predictor variable is shown in Table 5. After considering all predictor variables, almost 95% of the CHEESEHEAD19 measurements were discarded before applying the model to the measurements.

Fig. 7

Distribution of the predicting variables ($\langle {u}_{*}/{w}_{*}\rangle$, $\mathcal{H}$, $z/{z}_{i}$, $\langle \overline{\Delta \theta }\rangle$, $\langle \overline{\Delta q }\rangle$) used for the model training (gray) and of the predicting variables that occur in the CHEESEHEAD19 field measurements (blue). The limits of the predictor variables used for training the model are shown by the red dotted lines

Table 5 Percentage of CHEESEHEAD19 field measurements that fall into the range of the predictor variables used to train the model

In the field measurements, the total sensible and latent heat fluxes at the surface are not known. Therefore, it is only possible to compare the sum of measured sensible and latent heat fluxes and storage changes to the available energy at the surface ($R_{{{\text{net}}}} {-} G$). Figure 8 compares the measured turbulent fluxes and storage changes against the available energy and shows a large gap of 23.8% in the energy flux towards the atmosphere (left panel). In the right panel, the modelled dispersive fluxes are added to the measured turbulent fluxes, reducing the SEB gap to 18.6%.

Fig. 8

Comparison of measured turbulent heat fluxes (left) and measured turbulent and modelled dispersive heat fluxes (right) to the total energy flux to the atmosphere. The total energy flux to the atmosphere is calculated as the available energy at the surface ($R_{{{\text{net}}}} {-} G$) minus the storage change in form of sensible and latent heat (${{H}_{\Delta St}+\lambda E}_{\Delta St}$). The different colours represent the 16 individual eddy-covariance stations that were used for this analysis

Even though we do not know the actual breakdown of total available energy (${R}_{net}- G$) into sensible and latent heat, we can consider the contributions of each energy balance component shown in Fig. 9. The turbulent fluxes measured at the EC stations make up 27.48 ± 11.38% (${H}_{t}$) and 47.54 ± 18.33% (${\lambda E}_{t}$) of the total available energy at the surface, resulting in a Bowen ratio of 0.602 ± 0.458. The storage change accounts for 2.58 ± 3.85% (${H}_{\Delta St}$) and nearly 0% (${\lambda E}_{\Delta St}$). The modelled dispersive fluxes account for 1.54 ± 1.10% (${H}_{d,{\text{mod}}}$) and 5.53 ± 4.73% (${\lambda E}_{d,{\text{mod}}}$) of the total available energy. The Bowen ratio of the dispersive fluxes is 0.287 ± 0.252, which is considerably lower than the Bowen ratio observed in the turbulent flux measurements.

Fig. 9

Share of turbulent heat fluxes (${H}_{t}$, ${\lambda E}_{t}$), air storage change (${H}_{\Delta St}$, ${\lambda E}_{\Delta St}$) and modelled dispersive heat fluxes (${H}_{d,{\text{mod}}}$, ${\lambda E}_{d,{\text{mod}}}$) of the total available energy ($R_{{{\text{net}}}} {-} G$). The error bars represent the standard deviation of the sums shown in each bar

4 Discussion

4.1 The Model of Energy Transport by Secondary Circulations

Instead of modelling the entire energy imbalance as it was proposed by former models to close the energy balance gap (De Roo et al. 2018; Huang et al. 2008; Wanner et al. 2022b) we decided to predict only the contribution of energy transport by SCs. The storage change in the air layer below the measurement altitude is possible to measure through vertical profiles of $\theta$ and $q$, which is a more direct way to quantify it than modelling it. The storage change in the biomass is more difficult to determine by measurements. If the storage change cannot be measured or older measurements are to be corrected for which no storage change measurements are available, it must still be modelled to achieve SEB closure on a 30-min measurement basis. However, it is unlikely that the storage change depends on the same parameters as the energy transport through SCs, so these two aspects should be considered separately. Furthermore, even for observation periods longer than one day, the contribution of the storage change to the SEB gap becomes very small and can therefore be neglected if SEB closure is to be achieved only for longer time scales.

The cross-validation of the model for ${H}_{d}$ and ${\lambda E}_{d}$ (Fig. 2) shows that the correlation between predicted dispersive fluxes and true dispersive fluxes in the LES is very high for $H$ but considerably lower for $\lambda E$. We investigated whether the particularly large underestimates and overestimates of ${\lambda E}_{d}$ are linked to particularly high or low values of individual input variables. However, the values were always in the range of the input variables that achieved a suitable prediction of ${\lambda E}_{d,{\text{true}}}$. The large deviations are probably the result of a factor influencing ${\lambda E}_{d}$ that is not considered by the model.

One possible reason why ${H}_{d}$ prediction performs better than ${\lambda E}_{d}$ prediction is that the atmospheric stability, represented by $\langle {u}_{*}/{w}_{*}\rangle$, is directly linked to the magnitude of SCs and the magnitude of the sensible heat flux. A negative vertical gradient of $\theta$ leads to convective conditions under which the development of secondary circulations is favoured (De Roo et al. 2018; Huang et al. 2008; Wanner et al. 2022b) and also means that warmer air is available near the surface and can be transported upwards by those SCs.

The vertical moisture gradient, on the other hand, is not directly related to atmospheric stability but rather to the ratio between latent surface heat flux and dry air entrainment. For example, over vegetated, non-water-limited surfaces, the surface is typically a source of moisture and increases the humidity in the mixed layer. However, dry air entrainment at the boundary-layer top reduces the humidity in the mixed layer and especially at the boundary-layer top. While $\langle \overline{\Delta q }\rangle$ includes the change in the mixed layer, the effect of the stronger gradient near the boundary-layer top is ignored. If lapse-rate stratification causes the formation of SCs but $\langle \overline{\Delta q }\rangle =0$, the movement of air masses will not contribute to the transport of moisture. Including entrainment as a predictor variable could therefore potentially improve the model, especially for ${\lambda E}_{d}$.

This phenomenon is illustrated by the importance of input variables for predicting ${H}_{d}$ and ${\lambda E}_{d}$ shown in Fig. 2 where $\langle {u}_{*}/{w}_{*}\rangle$ and $\mathcal{H}$ have the strongest predictive power for ${H}_{d}$, but in comparison, the predictive power of $\langle {u}_{*}/{w}_{*}\rangle$ for ${\lambda E}_{d}$ is much lower. $\mathcal{H}$ is also the most important predictive variable for ${\lambda E}_{d}$. The normalized measurement height $z/\langle \overline{{z }_{i}}\rangle$ has an intermediate predictive power in both cases, which is due to increasing fraction of energy transport by SCs within the surface layers with increasing height.

The rather high scatter in the correlation of ${\lambda E}_{d,{\text{predicted}}}$ and ${\lambda E}_{d,{\text{true}}}$ does not have a negative effect if the total fluxes are considered (Fig. 2). The standard deviation of the corrected fluxes (${\lambda E}_{t}+{\lambda E}_{\Delta St}+{\lambda E}_{d,{\text{predicted}}}$) remains almost unchanged compared to the standard deviation of the uncorrected turbulent fluxes. For the sensible heat flux, the correction even provides a significant improvement, as the standard deviation of the corrected fluxes (${H}_{t}+{H}_{\Delta St}+{H}_{d,{\text{predicted}}}$) is significantly smaller than for the turbulent fluxes alone.

In Fig. 3 and Table 3, another interesting aspect can be observed: when considering domain-averaged values, the Bowen ratio of turbulent and dispersive fluxes are the same, although the gap between surface fluxes and turbulent fluxes is different for ${H}_{d}$ and ${\lambda E}_{d}$. This difference is compensated by the storage change alone. Thus, one could conclude that to close the SEB gap, it may be sufficient in many cases to measure ${H}_{\Delta St}$ and ${\lambda E}_{\Delta St}$ and fill the remaining gap according to the Bowen ratio of the measured turbulent heat fluxes. This approach has been discussed several times (Gebler et al. 2015; Hirschi et al. 2017; Mauder et al. 2007a, 2020; Mauder et al. 2013a, b; Twine et al. 2000). However, the relation between Bowen ratios of storage change and surface, turbulent, and dispersive heat fluxes is different in the more realistic CHEESEHEAD19 LES which is discussed in the next section. It furthermore remains questionable whether this assumption still holds if locally measured heat fluxes differ considerably from the average heat fluxes of the surroundings, which is typically the case in heterogeneous areas.

Due to the rather coarse resolution in the idealized LESs that were used to train the model, one has to assume that the strength of the SCs is underestimated, especially near the lower boundary of the domain. It is therefore likely that the model underestimates the transport of energy by SCs. The magnitude of this systematic error, however, is not known and requires further investigation in follow-up studies.

4.2 Application to the More Realistic CHEESEHEAD19 LES

Figure 4 shows that the model could be applied to almost all 30-min intervals with unstable conditions and for a wide range of measurement heights. A few observations near the canopy top had to be discarded because of the low values of $z/\langle \overline{{z }_{i}}\rangle$. However, this affected mostly measurement heights of less than 16.5 m, which corresponds to approximately 10 m above the canopy top. To avoid individual roughness elements affecting the measured turbulent fluxes, EC measurements should not be carried out within the roughness sublayer (Katul et al. 1999) and are often located more than 10 m above the canopy top at forest locations.

In comparison with the dispersive fluxes calculated from the CHEESEHEAD19 LES output, the model slightly overestimates ${\lambda E}_{d}$ and clearly overestimates ${H}_{d}$ (Fig. 5), resulting in a general overestimation of dispersive fluxes (Fig. 6) and a slightly higher Bowen ratio (Table 4). The fact that ${H}_{d,{\text{mod}}}$ and ${\lambda E}_{d,{\text{mod}}}$ are slightly larger than the actual fluxes could be due to non-cyclic boundary conditions in the CHEESEHEAD19 LES. This arrangement raises the possibility that a small share of energy is transported by horizontal advection and is therefore not captured in the dispersive fluxes. Another reason could be the different setup of the simulations. In the idealized simulations, the fluxes were prescribed at the surface, whereas in the realistic simulations, the surface fluxes were provided by a combination of LSM and PCM. Wanner et al. (2022a) showed that the use of LSM and PCM increases the dispersive heat fluxes directly above the canopy but decreases the dispersive fluxes further up in the ABL, compared to dispersive fluxes produced in simulations with prescribed surface fluxes, owing to feedbacks between atmosphere and surface.

In contrast to the results from the idealized LESs, $\beta (\langle {F}_{d,{\text{LES}}}\rangle )$ does not equal $\beta (\langle {F}_{t}\rangle )$ in the CHEESEHEAD19 LES but is considerably lower, indicating that SCs have a larger relative share in the transport of latent heat than in the transport of sensible heat. It follows that the Bowen ratio approach to fill the SEB gap is not so well suited under more realistic conditions. Our dispersive flux model is capable of partially capturing the difference between $\beta (\langle {F}_{d,{\text{LES}}}\rangle )$ and $\beta (\langle {F}_{t}\rangle )$, but due to the strong overestimation of the sensible dispersive heat flux by roughly 18%, the partitioning of dispersive fluxes in the realistic LES is not ideally captured by the model.

Another factor that could alter the partitioning is the influence of entrainment on the transport of energy by secondary circulations (Gao et al. 2017; Huang et al. 2008; Mauder et al. 2020) which is not considered in our model. A temperature or humidity gradient in the boundary layer is the basic prerequisite for any transport of sensible or latent energy through SC which is why we included $\langle \overline{\Delta \theta }\rangle$ and $\langle \overline{\Delta q }\rangle$ as predictors in our model. The properties of the air mixed into the boundary layer at the upper boundary should also affect the transport of sensible heat or water vapor. Since $\langle \overline{\Delta \theta }\rangle$ and $\langle \overline{\Delta q }\rangle$ only represent the lower half of the atmospheric boundary layer (see Eqs. 16–17), this influence is only partially considered in the model and could also contribute to the underestimation of the dispersive fluxes. Since the ABL is confined by an inversion at the top, the influence of entrainment on the ${H}_{d}$ may be quite small. However, the humidity above the boundary layer is highly variable, so the effect of entrainment could also be a reason for the high uncertainty in the prediction of ${\lambda E}_{d}$. The heat flux profiles (not shown) confirm that the flux regime in the CHEESEHEAD19 LES was driven rather by dry air entrainment at the ABL top than by the surface fluxes at some times. As already discussed in the previous section, including entrainment as a predictor variable might therefore improve the model performance. For instance, this could be considered by the ratio of entrainment flux and the surface flux for sensible and latent heat.

Furthermore, with non-cyclic boundary conditions it is possible that weather fronts pass through the domain which can carry warmer/cooler or moister/dryer air into the domain, affecting $\overline{w }$, $\overline{\theta }$, and $\overline{q }$ used to calculate the dispersive fluxes. In the CHEESEHEAD19 LES, a front passed through the domain in the afternoon on the first day, causing the boundary layer to collapse at 14.5 h simulated time which corresponds to 1430 LT, which is shown by the increase of $z/\langle \overline{{z }_{i}}\rangle$ (Fig. 4). Figure 13 (Appendix 2) shows that the surface fluxes started decreasing at 1300 LT, indicating that advection may already have played a minor role, affecting ${H}_{d,{\text{LES}}}$ and ${\lambda E}_{d,{\text{LES}}}$. The effect of weather fronts passing by is generally less relevant for EC measurements, as they would typically be discarded in the affected periods, due to the violation of the stationarity requirement (Mauder et al. 2006).

4.3 Application to the CHEESEHEAD19 Field Measurements

The application of the model to field measurements was very limited because the ranges of the predictor variables in the field measurements were significantly larger than covered by the idealized LESs used to train the model (Fig. 7). The ranges of $\langle {u}_{*}/{w}_{*}\rangle$, $\mathcal{H}$ and $\langle \overline{\Delta q }\rangle$ encountered in the ERA5 reanalysis data is much larger than in the idealized LES. However, this seems to be caused by extreme cases and outliers since a considerable number of observations (45.06%, 99.77%, and 67.94%, respectively) were covered by the training data (Table 5). The range of $z/\langle \overline{{z }_{i}}\rangle$ encountered in the field is only slightly larger than in the idealized LES. Nevertheless, only 37.90% were covered by the training data (Table 5). This is due to the low measurement heights in some of the field stations (12 m at NW2 and SE5 and 3 m at NW3 and SE5) whose data were entirely discarded. Such low measurement heights could not be covered by the idealized LES due to the coarse grid resolution. Most measurements had to be discarded due to insufficient coverage of $\langle \overline{\Delta \theta }\rangle$, as only 27.69% of the observed values were covered by the idealized LES (Table 5).

To investigate whether the large ranges in predictor variables are realistic, we compared the predictor variables derived from the ERA5 reanalysis data to the predictor variables derived from the CHEESEHEAD19 LES for 22–23 August 2019 (Fig. 10). On average, they show a good agreement in $\mathcal{H}$ and $\langle \overline{{z }_{i}}\rangle$ where the values are distributed evenly around unity, although ERA5 does not capture the variability in $\langle \overline{{z }_{i}}\rangle$ as well as the CHEESEHEAD19 LES. Compared to the CHEESEHEAD19 LES, ERA5 underestimates $\langle {u}_{*}/{w}_{*}\rangle$ and overestimates $\langle \overline{\Delta \theta }\rangle$ and$\langle \overline{\Delta q }\rangle$. The comparison of hourly vertical profiles (Fig. 14, Appendix 3) shows that the overestimation of $\langle \overline{\Delta \theta }\rangle$ results mainly from a stronger increase in theta near the surface, whereas the profiles agree very well within the mixed layer (Fig. 11).

Fig. 10

Comparison of predictor variables for the dispersive flux model from the CHEESEHEAD19 LES (x-axis) and ERA5 reanalysis data (y-axis) for all 30-min intervals on 22–23 August used for the analysis. Note that the second panel shows $\langle \overline{{z }_{i}}\rangle$ instead of $z/\langle \overline{{z }_{i}}\rangle$ for better comparability

Fig. 11

Comparison of hourly averaged vertical profiles of potential temperature ($\langle \overline{\theta }\rangle$) and mixing ratio ($\langle \overline{q }\rangle$) between the CHEESEHEAD LES and ERA5 reanalysis data for 23 August, 2019

The CHEESEHEAD19 LES was validated against field measurements and the domain-averaged vertical profiles showed good agreement with radiosonde measurements (Paleri et al. (2023)). Nevertheless, it must be noted, that the domain was mostly forested with an average canopy height of 22.08 m. The active surface is therefore not clearly defined and the lowest grid points receive less radiation. $\langle \overline{\theta }\rangle$ may therefore be slightly underestimated near the surface.

Figure 8 shows that adding the modelled energy transport by secondary circulations considerably decreases the SEB gap from 23. 8% on average to 18.6% on average but the SEB is still not closed. As mentioned in Sect. 4.1, one reason for the remaining gap is that the model might underestimate the transport by SCs due to the coarse grid spacing. However, there are more reasons why considering the energy transport by SCs alone does not result in SEB closure.

Because the model predicts only the dispersive heat fluxes and not the entire SEB gap, the storage of energy in the underlying air volume and canopy must be measured at tall EC stations since it also contributes significantly to the SEB gap. The measurement of the energy storage in the air volume beneath an EC station can be realized by simple profile measurements of temperature and humidity. This is already standard in some EC stations (Heiskanen et al. 2022) and was also included in the CHEESEHEAD19 measurements. However, the biomass storage change is typically not measured at EC stations and adds uncertainty to the energy storage quantification. It was not included in the energy storage measurements at the CHEESEHEAD19 sites, though tree biomass heat storage was measured at several sites subsequent to the campaign, where it averaged 6.5% of the available energy (Butterworth et al. 2024). This agrees with other studies which have found the biomass storage change to be of the same magnitude as the storage change in the air (Lindroth et al. 2010) or even twice as high (Haverd et al. 2007) at forest locations. Figure 9 shows that the addition of modelled dispersive heat fluxes to measured heat fluxes and air storage change decreases the SEB gap from 22.82 ± 17.67% to 15.75 ± 19.40%. Including the biomass storage change would further decrease the SEB gap to roughly 9% on average.

As discussed in Sect. 4.1, a slight underestimation of the dispersive fluxes by the model is expected due to the coarse grid spacing in the idealized LESs providing the training data. However, there are some more minor factors that contribute to the SEB gap that were not considered in this analysis.

First, the model only considers the effect of atmospheric stability and thermal surface heterogeneity on the energy transport by secondary circulations, which were identified as the major factors. However, topography effects can also enhance the energy transport of energy by SCs (Finnigan et al. 2003) but are not included in the model. Even though the measurement area was chosen in part because of its weak topography, the area in which the CHEESEHEAD19 campaign took place is not entirely flat. This may have strengthened the SCs, especially near the numerous water bodies in the domain which would also explain why the dispersive fluxes in the field measurements are larger than in both the idealized and CHEESEHEAD19 LESs.

Second, the turbulent heat fluxes might be underestimated as CSAT3AW (Campbell Scientific) sonic anemometers were used. For this type of sonic anemometer, a correction to account for transducer shadowing was developed that increases the fluxes by up to 5% (Horst et al. 2015) which was not applied to the CHEESEHEAD19 field measurements. Also, minor contributions to the SEB gap are not considered, like energy consumption by photosynthesis, which is estimated to account for roughly 1% of ${R}_{net}$ (Finnigan 2008). Taking these factors into account, the remaining SEB gap would be only about 3%, which suggests that the underestimation of energy transport by SCs by our model is quite small.

4.4 Different Data Availability in Idealized LES, More Realistic LES, and Field Measurements

Fundamental differences in data availability in the idealized and more realistic LES and field measurements complicate the accurate application of the model. This includes the determination of $\mathcal{H}$, the true dispersive fluxes and the vertical differences $\langle \overline{\Delta \theta }\rangle$ and $\langle \overline{\Delta q }\rangle$.

The calculation of $\mathcal{H}$ involves $\Delta \overline{T }$, $\langle \overline{{T }_{{\text{s}}}}\rangle$, and ${L}_{h}$. All three parameters are calculated based on the two-dimensional surface temperature. In the idealized LES, the surface temperature is clearly defined as the temperature at the lower boundary of the domain. In the CHEESEHEAD19 simulations, where a plant canopy model has been used in the forested areas, the surface is not so clearly defined. The temperature at the lower boundary of the domain is not very meaningful because it is mostly shaded and the majority of radiative transfer happens at the canopy level. We therefore used the air temperature at the top of the vegetation instead of the actual surface temperature as ${T}_{{\text{s}}}$, but this is based on the assumption that the vegetation has the same temperature as the air and introduces additional uncertainty. In field measurements, ${T}_{{\text{s}}}$ is difficult to determine at sufficiently high spatial and especially temporal resolution. Therefore, we used the surface-temperature maps from Desai et al. (2021), which are a fusion data product using land-surface models, satellite and hyperspectral imagery to apply the model to the CHEESEHEAD19 field measurements.

The dispersive fluxes can be computed directly as the spatial covariance of $w$ and $\theta$ or $w$ and $q$ in the idealized LESs with cyclic boundary conditions and thus quasi-infinite horizontal extent. In the realistic LES, the dispersive fluxes can also be computed as spatial covariance in a defined area. This area must be sufficiently large to fully cover the horizontal extent of the secondary circulations, similarly to how the averaging period in classical EC measurements must theoretically be sufficiently long to cover all relevant time scales. Since the horizontal extent of secondary circulations can reach about 2–3 times ${z}_{i}$ (Paleri et al. 2022a; Stull 1988), we recommend using an area with an edge length of at least 4 times ${z}_{i}$ to calculate the dispersive fluxes. If the area is too small, SCs partially contribute to horizontal transport, i.e., advection, that is not captured by the spatial covariance of $w$ and $\theta$ or $q$. If the area is very large or includes an area where land cover or topography changes significantly the resulting dispersive flux is not representative of the area in which the EC measurement takes place. For typical single-tower field measurements, the dispersive flux cannot be calculated directly, as the calculation of covariances would require high-resolution spatial measurements of $w$, $q$ and $\theta$. Instead, the amount of energy transported by the SCs must be calculated indirectly as a residual from the available energy at the surface ($R_{{{\text{net}}}} {-} G$) minus the energy stored in the air volume between the surface and the measurement height (${H}_{\Delta St}+{\lambda E}_{\Delta St}$) and the turbulent transport of energy (${H}_{t}+{\lambda E}_{t}$). A drawback of this approach is the scale mismatch between the measurement of ${R}_{net}$ and $G$, which is only representative for the location of the EC station, and $H$ and $\lambda E$, which reflect the energy flux of the entire footprint, which covers a much larger area depending on the measurement height and atmospheric stability (Kljun et al. 2015).

For the model training, the output from the idealized LESs was used where the vertical differences $\langle \overline{\Delta \theta }\rangle$ and $\langle \overline{\Delta q }\rangle$ were calculated as the difference between surface values and the 0.5 $\langle \overline{{z }_{i}}\rangle$. Since surface values are not available in the ERA5 reanalysis data, we used the 2 m temperature and humidity measurements instead to predict the dispersive fluxes in the CHEESEHEAD19 measurements. Under unstable conditions, the temperature gradient near the surface is very steep. Thus, the 2 m temperature is expected to be lower than the air temperature directly above the surface, resulting in an underestimation of the vertical temperature difference between the surface and the middle of the boundary layer. Over vegetated surfaces, which typically serve as a source of moisture unless they experience water stress, using the 2 m humidity instead of a near-ground measurement also results in an underestimation of the vertical difference. However, as shown in Fig. 10, $\langle \Delta \overline{\theta }\rangle$ derived from ERA5 reanalysis data is not underestimated but overestimated compared to the CHEESEHEAD19 LES.

In the more realistic CHEESEHEAD19 LES, a PCM is used in forested areas, which is why the active surface is not as clearly defined as in the idealized LES. This increases the uncertainty in the calculation of ${T}_{{\text{s}}}$, $\langle \Delta \overline{\theta }\rangle$ and $\langle \Delta \overline{q }\rangle$ and $\langle {u}_{*}/{w}_{*}\rangle$, as well as the surface fluxes.

4.5 Feasibility of the Model Application to Eddy-Covariance Stations

Single point EC field measurements typically only represent a limited area, referred to as footprint. The size of this area depends on various factors such as measurement height, atmospheric stability, and horizontal wind speed (Kljun et al. 2015), but it is always only a subset of the area that influences the development of SCs. Since the horizontal extent of SCs can reach 2–3 times ${z}_{i}$, they can span multiple kilometres and the area that has an effect on their development is correspondingly large. Therefore, EC measurements are likely to differ from the average values representing the entire area and are not suited as predicting variables for a model based on domain-averaged values.

This is why we used the ERA5 reanalysis data to provide the majority of the predictor variables for the application of the model to the CHEESEHEAD19 EC measurements. One advantage of the ERA5 reanalysis data is that it is available in all locations where EC measurements are carried out and thus can be used to predict dispersive fluxes at any tower without installing additional measurement instruments. This also facilitates the prediction of dispersive fluxes for EC measurements carried out in the past for which no field measurements of predictor variables are available. Since the ERA5 reanalysis data is available for the past 80 decades it can be used to consistently improve the energy-balance closure in long existing time series. However, with a spatial resolution of 0.25°, one grid cell in the ERA5 data is representative of up to 28 × 28 km², which might include landscapes that are not representative of the surroundings of an EC tower.

The only parameters not derived from the ERA5 reanalysis data were $\Delta \overline{T }$, $\langle \overline{{T }_{{\text{s}}}}\rangle$, and ${L}_{h}$ used to calculate the thermal heterogeneity parameter as their calculation requires spatially highly resolved surface-temperature maps. We used the land-surface temperature fusion maps provided by Desai et al. (2021) which are derived by combining the information gathered from different satellite observations with high temporal resolution (NLDAS-2 (Xia et al. 2012), GOES-R (Yu et al. 2009)) and high spatial resolution (ECOSTRESS (Hulley et al. 2022)). Desai et al. (2021) showed that these maps represent the spatial and temporal variation in surface temperature in the CHEESEHEAD19 domain. Their approach can be used to generate land-surface temperature fusion maps with a spatial resolution of 50 m and a temporal resolution of 1 h for any location where temporally frequent geostationary (such as GOES) and high-spatial resolution less frequent land surface-temperature data (such as ECOSTRESS) are available and therefore can as well be derived for many EC stations without carrying out additional measurements.

5 Conclusion

We have developed a model to predict 30-min dispersive heat fluxes, i.e., the energy transport by SCs. A Python script to apply the model, including the training dataset, is included in the supplements.

By applying it to the CHEESEHEAD19 LES, we have shown that it reproduces the partitioning into sensible and latent heat fluxes quite well. The application to CHEESEHEAD19 field measurements showed that the model currently covers only a limited range of atmospheric conditions and is only applicable to measurement heights where ${z}_{{\text{m}}}$-${z}_{{\text{d}}}$ > 10 m. Therefore, to predict dispersive fluxes under all typical conditions at eddy covariance stations, the training data set must be extended to cover a wider range of $\langle \overline{\Delta \theta }\rangle$, $\langle \overline{\Delta q }\rangle$, $\mathcal{H}$, and $z/\langle {z}_{i}\rangle$.

However, application to the measurements that were within the model limits showed that the modelled dispersive fluxes resulted in a significant reduction in the SEB gap, but a SEB gap of 18.6% still remained. A variety of possible reasons were discussed, including the low resolution of the LESs the training data was extracted from, the different availability of information on vertical differences of $\langle \overline{\theta }\rangle$ and $\langle \overline{q }\rangle$ in the LES and the ERA5 reanalysis data, and uncertainties associated with the use of modelled surface temperature and atmospheric variables as predictor variables. The dispersive flux model could therefore be further improved by increasing the resolution of the LESs that provide the training data, which will allow for an enhanced representation of SCs near the surface and the differences of $\langle \overline{\theta }\rangle$ and $\langle \overline{q }\rangle$ can be defined in accordance to data availability in field measurements.

We conclude that these factors likely cause a slight underestimation of the dispersive fluxes by the model. However, a large portion of the remaining gap could be filled by adding the ignored biomass storage change, which is estimated to account for 6.5% of the total available energy at 30-min intervals.

We have also shown that it is possible to apply this model of dispersive heat fluxes to field measurements without performing any additional field measurements. The application of the model is based on ERA5 reanalysis data and remote sensing products that are available for most EC stations around the world and can also be used to model the dispersive fluxes retroactively.

Appendices

Appendix 1: The Idealized Large-Eddy Simulations

Figure 11 shows that even with horizontally homogeneous surface fluxes (Table 6), a weak pattern of cells (low ${U}_{g}$) or stripes (high ${U}_{g}$) develops. This pattern is superimposed over the much stronger pattern resulting from the heterogeneous surface fluxes. However, the surface temperature still exhibits a pattern of accurate squares with a low ${U}_{g}$, whereas the surface temperature pattern becomes more blurred when ${U}_{g}$ is high (Fig. 12).

Table 6 Characteristic values of each of the 148 idealized simulations

Fig. 12

The left two columns show prescribed surface fluxes ($\overline{{H }_{{\text{s}}}}$, $\overline{{\lambda E }_{{\text{s}}}}$) from exemplary simulations with the same Bowen ratio ($\beta$). The right two columns show the resulting surface temperatures ($\overline{{T }_{{\text{s}}}}$) for simulations with the lowest (${U}_{g}$ = 0.5 m s⁻¹) and highest (${U}_{g}$= 9 m s⁻¹) geostrophic wind speed. The top row shows simulations with homogeneous surface fluxes. The rows below show simulations with heterogeneous surface fluxes with increasing patch size (200 m, 400 m, 800 m)

Appendix 2: The More Realistic CHEESEHEAD LES

Figure 13 shows the time series of horizontally domain-averaged surface, turbulent and dispersive heat fluxes with $\langle {H}_{{\text{s}}}\rangle$ > 10 W m⁻². Only grid levels above the average canopy height ${z}_{{\text{c}}}$ are considered.

Fig. 13

Profiles of 30-min and domain-averaged potential temperature (θ), mixing ratio (q), and horizontal wind speed (U) for two example simulations. The simulation with ID 98 has very low horizontal wind speed and high sensible surface heat flux, and the simulation with ID 62 has very high horizontal wind speed and low sensible surface heat flux

Appendix 3: The ERA5 Reanalysis Data

See Fig. 14.

Fig. 14

Time series of the surface fluxes ($\langle {H}_{{\text{s}}}\rangle$ and $\langle {\lambda E}_{{\text{s}}}\rangle$), turbulent flux contributions ($\langle {H}_{t}\rangle$ and $\langle {\lambda E}_{t}\rangle$) and dispersive flux contributions (${H}_{d,{\text{LES}}}$ and ${\lambda E}_{d,{\text{LES}}}$) that were encountered in the CHEESEHEAD simulations