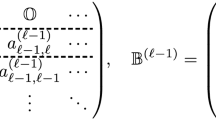A note on approximate Jacobians of implicit Runge–Kutta methods and convergence of modified Newton iterations

Abstract

We consider the application of implicit Runge–Kutta (IRK) methods to systems of implicit ordinary differential equations (ODEs). We are especially interested in the situation when stiffness arises. We show that the eigenvalues of major families of A-stable implicit Runge–Kutta methods are simple and have non-negative real part. We give necessary and sufficient conditions for the invertibility of approximate Jacobians of IRK methods. The main result of this note provides some sufficient conditions to ensure local contractivity, hence convergence, of modified Newton iterations of IRK methods for stiff ODEs with step size conditions independent of stiffness.

A Appendix

In this appendix we show that the two concepts of irreducibility for an IRK method and irreducibility of the corresponding rational stability function are unrelated, thus disproving the statement made in [6, p.368] that “Irreducibility gives that the fraction cannot be reduced”.

The stability function of s-stage IRK methods is given by $R(z)=P(z)/Q(z)$ where $P(z)=\det (I_s-z(A-{ 1 \hspace{-2.89993pt}\textrm{l}_s}b^T))$, $1 \hspace{-2.89993pt}\textrm{l}_s:=(1,\ldots ,1)\in {\mathbb {R}}^s$, and $Q(z)=\det (I_s-zA)$. For example consider diagonally implicit Runge–Kutta (DIRK) methods with $s=2$ stages. Their IRK matrix A is lower triangular

$$\begin{aligned} A= \left[ \begin{array}{cc} a_{11} &{} 0 \\ a_{21} &{} a_{22} \end{array}\right] . \end{aligned}$$

For any 2-stage IRK method to be consistent we must have $b_2=1-b_1$. We assume $b_1\not \in \{0,1\}$ otherwise the DIRK method would be reducible. We have

$$\begin{aligned}{} & {} P(z)=\det \left( \left[ \begin{array}{cc} 1-z(a_{11}-b_1) &{} -z( 0-(1-b_1)) \\ -z(a_{21}-b_1) &{} 1-z(a_{22}-(1-b_1)) \end{array}\right] \right) ,\ \\ {}{} & {} Q(z)=(1-za_{11})(1-za_{22}). \end{aligned}$$

Hence assuming $a_{11}\not =0$ and $a_{22}\not =0$ the roots of Q(z) are simply $z_1=1/a_{11}$ and $z_2=1/a_{22}$. We will choose the coefficients of the DIRK method such that we also have $P(z_1)=0$ which will thus imply that the stability function R(z) is reducible, henceforth providing our sought counterexample. We have

$$\begin{aligned} P(z_1)\!=\! & {} P(1/a_{11})=\frac{1}{a_{11}^2} \det \left( \left[ \begin{array}{cc} b_1 &{} 1-b_1 \\ b_1-a_{21}\ {} &{} a_{11}-a_{22}+1-b_1 \end{array}\right] \right) \\\!=\! & {} \frac{1}{a_{11}^2}(b_1(a_{11}-a_{22}+1-b_1)+(b_1-1)(b_1-a_{21})). \end{aligned}$$

One can even require the DIRK method to be of order 2 though it is not necessary for our purpose here. For order 2 we must have the additional condition

$$\begin{aligned} b_1a_{11}+(1-b_1)(a_{21}+a_{22})=\frac{1}{2}. \end{aligned}$$

This condition implies that $P(z_1)=0$ is now simply equivalent to having $a_{22}=1/2$. Hence, we are left with the condition

$$\begin{aligned} b_1a_{11}+(1-b_1)\left( a_{21}+\frac{1}{2}\right) =\frac{1}{2}. \end{aligned}$$

(A.1)

Solving for example for $a_{21}$ we obtain

$$\begin{aligned} a_{21}=-\frac{1}{2}+\frac{1/2-b_1a_{11}}{1-b_1}. \end{aligned}$$

We have found solutions with two (almost) free parameters $b_1\not \in \{0,1\}$ and $a_{11}\not \in \{0,1/2\}$. Choosing for example $a_{11}=1/3$ and $b_1=3/4$ leads to the following irreducible DIRK method with Radau II nodes and weights

$$\begin{aligned} \begin{array}{c|cc} 1/3 &{} 1/3 &{} 0 \\ 1 &{} 1/2 &{} 1/2 \\ \hline &{} 3/4 &{} 1/4 \end{array} \end{aligned}$$

with reducible stability function $R(z)=P(z)/Q(z)$ where

$$\begin{aligned} P(z)=1+z/6-z^2/6=(1-z/3)(1+z/2),\qquad Q(z)=(1-z/3)(1-z/2) \end{aligned}$$

which is even A-stable (!) since $R(z)=(1+z/2)/(1-z/2)$ is the (1, 1)-Padé approximation to $e^z$. Notice here that the IRK matrix A here is nonsingular, its eigenvalues are both strictly positive (1/3 and 1/2), although the DIRK method does not satisfy the conditions of Theorem 2.1. In fact from

$$\begin{aligned} P(z)=1+(1/2-a_{11})z+cz^2=(1-a_{11}z)(1-\alpha z)=1-(a_{11}+\alpha )z+a_{11}\alpha z^2 \end{aligned}$$

we find that $\alpha =-1/2$ and thus

$$\begin{aligned} P(z)=(1-a_{11}z)(1+z/2) \end{aligned}$$

for any choice of $a_{11}$ and $b_1$. This also follows from (A.1) by calculation. The corresponding DIRK methods are all A-stable since $R(z)=(1+z/2)/(1-z/2)$ is the (1, 1)-Padé approximation to $e^z$ even when choosing a negative value for $a_{11}$. For example choosing now instead the absurd value $a_{11}=-1/2$ and $b_1=1/3$ leads to the following irreducible DIRK method

$$\begin{aligned} \begin{array}{c|cc} -1/2 &{} -1/2 &{} 0 \\ 1 &{} 1/2 &{} 1/2 \\ \hline &{} 1/3 &{} 2/3 \end{array} \end{aligned}$$

with reducible stability function $R(z)=P(z)/Q(z)$ where

$$\begin{aligned} P(z)=1+z+z^2/4=(1+z/2)^2,\qquad Q(z)=(1+z/2)(1-z/2). \end{aligned}$$

Notice that the IRK matrix A here is nonsingular, one of its eigenvalues is strictly negative ($-1/2$) and the other one is strictly positive (1/2). Of course this DIRK method also does not satisfy the conditions of Theorem 2.1.

As a final note consider the 2-stage Lobatto IIIB method

$$\begin{aligned} \begin{array}{c|cc} 0 &{} 1/2 &{} 0 \\ 1 &{} 1/2 &{} 0 \\ \hline &{} 1/2 &{} 1/2 \end{array} \end{aligned}$$

which is based on the trapezoidal rule quadrature formula. It is a reducible method when applied to autonomous ODEs $dx/dt=f(x)$ and it is equivalent to the implicit midpoint rule, but its stability function is irreducible.