Skip to main content
SpringerLink
Log in

Experimenting with Triangles

  • Original Paper
  • Published:
Axiomathes Aims and scope Submit manuscript

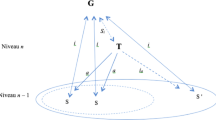
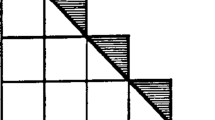
Abstract

Is there anything like an experiment in mathematics? And if this is the case, what would distinguish a mathematical experiment from a mathematical thought experiment? In the present paper, a framework for the practice of mathematics will be put forward, which will consider mathematics as an experimenting activity and as a proving activity. The relationship between these two activities will be explored and more importantly a distinction between thought-experiments, real experiments, quasi experiments and proofs in pure mathematics will be provided. To do so, three examples of experimenting with triangles will be introduced and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. This is not new for mathematics from the point of view of philosophy of science, which rarely addresses the specificities of this discipline compared to other scientific practices.

  2. Here are the groups of TEs as defined by Anapolitanos (1991): TEs (1) “usually performed in a conceptual framework which has not been yet theoretically solidified”; (2) “performed in a conceptual framework provided by a fixed mathematical theory; (3) “performed fervently during and immediately after a foundational crisis”; (4) “spurred by the intrinsic possibility of proving or disproving a postulate or a sentence, which mathematicians under certain circumstances come to think as basic, from the axioms of a more or less given mathematical theory”; (5) “triggered and influenced—among other things—by philosophical considerations of a quite revolutionary nature”; (6) “induced by the need to specify a new conceptual framework easier to work with in a specific area”.

  3. A different question is how experimental methods coming from the social sciences can be used to study the practice of mathematics, analogously to what happens in so-called “experimental philosophy”. On this point, see Löwe and van Kerkhove (2019).

  4. Ferréiros (2016) as well defends the idea that advanced mathematics—differently from elementary mathematics—is based on hypotheses, that is, on hypothetical assumptions. As he explains, this refers to a long tradition of reflection on mathematical knowledge, including Riemann, Peirce, Poincaré, Weyl, Quine, and Putnam.

  5. On this point, see Gowers (2022).

  6. Discussing Greek mathematics, Netz (1999) introduces the principle of “repeatability” of proof, of which the generalizability of result is a derivation.

  7. Despite being a Platonist, also Brown is very close to Lakatos’ view. See on this point Brown (2022).

  8. Several possible taxonomies such as the ones presented in Anapolitanos (1991) or van Bendegem (forthcoming) are indeed "extensions" of Lakatos' ideas.

  9. The role and possibly the limits of the use of visualizations is still a core issue for mathematics education: more experimental work should be done on this point. In a more recent paper, Bråting (2012) discusses other examples in the light of the historical development of mathematics to show the importance of interpretation when it comes to visualizations, by arguing, contra Giaquinto, that a possible division between “visible mathematics” and “less visible mathematics” is misleading.

  10. Nersessian (2018) goes on by attributing an important role to TEs-narratives, which lead to the creation and the manipulation of the mental models. In this article, I will not focus on this element; however, I agree that narratives are an interesting topic to work on also for mathematics, not only for experiments but also for proofs. This is matter of further research.

  11. Friedman and Rittberg (2021) discuss paper folding as a form of “material reasoning”, that is, as a more reliable process than what I am describing here, having a strong epistemic value. In their view, material folding constitutes a third kind of mathematical reasoning besides propositional and diagrammatic reasoning. In order to show that paper folding is indeed a mathematical practice, they present a brief survey of the history of paper folding, concentrating mainly on the first third of the twentieth century.

  12.  I thank Uriah Kriegel for this example.

  13. I thank Jean Paul van Bendegem and Colin Rittberg for having pointed out to me this illustrative example.

  14. I thank Mario Piazza for this metaphor, which we presented in our book (Giardino and Piazza 2008).

  15. I thank Anouk Barberousse for having pointed out this issue to me.

  16. Larvor (2013) argues that some arguments in mathematics are not in principle verbal but inscribed, that is, a form of syntactic reasoning exploiting mathematical notation. Since he focuses on the written formalisms, I would suggest that what he refers to is a limit case between QEs and REs, where the formalism is more than a simple material support but becomes a material anchor.

  17. De Toffoli (2021) argues that the main function of mathematical justification deriving from rigorous proofs is to guarantee that the mathematical community can correct errors that inevitably arise from our human fallible practices. Hamami (to appear) recognizes that there are non-deductive reliable methods, but that it is thanks to deductive methods proofs that contain repairable mistakes can be corrected, and proofs that cannot be repaired will be rejected.

  18. Rittberg et al. (2020) aim to show that epistemic injustice can manifest itself also in the practice of mathematics, and to do so the authors discuss a case where a FP is subject to doubt, since it proves a mathematical statement that is considered by a part of the community so obvious—in relation to “the existing body of knowledge” of the field—that it would need no proof.

  19. On the relationship between rigorous and formal proofs, considering the practice of proving, see Hamami (2022).

  20. The aim of this article is in spirit very close to van Bendegem (forthcoming), which presents an alternative general and complex scheme to accommodate mathematical thought experiments.

References

  • Anapolitanos DA (1991) Thought experiments and conceivability conditions. In: Horowitz T, Massey G (eds) Thought experiments in science and philosophy. Rowman and Littlefield, Savage, pp 87–98

    Google Scholar 

  • Bråting K (2012) Visualizations and intuitive reasoning in mathematics. Math Enthus 9(1):1

    Article  Google Scholar 

  • Bråting K, Pejlare J (2008) Visualizations in mathematics. Erkenntnis 68(3):345–358

    Article  Google Scholar 

  • Brown JR (1991) Laboratory of the mind: thought experiments in the natural sciences. Routledge, London

    Google Scholar 

  • Brown JR (1999) Philosophy of mathematics: an introduction to a world of proofs and pictures. Routledge, London

    Google Scholar 

  • Brown JR (2011) The laboratory of the mind: thought experiments in the natural sciences, 2nd edn. London, Routledge

  • Brown JR (2022) Rigour and thought experiments: burgess and Norton. Axiomathes

  • Buzzoni M (2011) On mathematical thought experiments. Epistemologia 34:5–32

    Google Scholar 

  • Buzzoni M (2021) Mathematical vs empirical thought experiments. In: Experience, abstraction, and the scientific image of the world. Festschrift for Vincenzo Fano on his 60th Birthday, Milano, Franco Angeli, pp 215–225

  • De Toffoli S (2021) Groundwork for a fallibilist account of mathematics. Philos Q 7(4):823–844

    Google Scholar 

  • Ferréiros J (2016) Mathematical knowledge and the interplay of practices. Princeton University Press, Princeton

    Book  Google Scholar 

  • Frake C (1985) Cognitive maps of time and tide among medieval seafarers. Man 20:254–270

    Article  Google Scholar 

  • Freiling C (1986) Axioms of symmetry: throwing darts at the real number line. J Symb Logic 51(1):190–200

    Article  Google Scholar 

  • Friedman M, Rittberg CJ (2021) The material reasoning of folding paper. Synthese 198:6333–6367

    Article  Google Scholar 

  • Giaquinto M (2007) Visual thinking in mathematics. An epistemological study. Oxford University Press, Oxford

    Book  Google Scholar 

  • Giardino V, Piazza M (2008) Senza Parole. Ragionare con le Immagini (Without Words. Reasoning with Images), (Milano: Bompiani)

  • Gowers T (2022) What makes mathematicians believe unproved mathematical statements? Ann Math Philos 1

  • Hamami Y (2022) Mathematical rigor and proof. Rev Symb Logic 15(2):409–449

    Article  Google Scholar 

  • Hamami Y (to appear) Proofs, reliable processes, and justification in mathematics. Br J Philos Sci. https://doi.org/10.1086/715137

  • Hutchins E (2005) Material anchors for conceptual blends. J Pragmat 37(10):1555–1577

    Article  Google Scholar 

  • Klein F (1908, 2004) Elementary Mathematics from an Advanced Standpoint. Courier Dover Publications, Mineola (translated by E. R. Hedrick and C. A. M. Noble)

  • Kosslyn S (1980) Image and mind. Harvard University Press, Cambridge

    Google Scholar 

  • Lakatos I (1976) Proof and refutations: the logic of mathematical discovery. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Larvor B (2013) What philosophy of mathematical practice can teach argumentation theory about diagrams and pictures. In: Aberdein A, Dove I (eds) The argument of mathematics. Logic, epistemology, and the unity of science, vol 30. Springer, Dordrecht

    Google Scholar 

  • Löwe B, van Kerkhove B (2019) Methodological triangulation in empirical philosophy of mathematics. In: Aberdein A, Inglis M (eds) Advances in experimental philosophy of logic and mathematics. Bloomsbury Publishing, New York, pp 15–38

    Google Scholar 

  • Mach E (1905) On thought experiments. In: Knowledge and error: sketches on the psychology of enquiry. Reidel Publishing Company, Dordrecht (translated by T. J. McCormack, D.)

  • Nersessian NJ (1992) In the theoretician’s laboratory: thought experimenting as mental modeling. Proc Philos Sci Assoc 2:291–301

    Google Scholar 

  • Nersessian NJ (2018) Cognitive Science, Mental Modeling, and Thought Experiments. In: Stuart MT, Fehige Y, Brown JR (eds) The Routledge companion to thought experiments. Routledge, London, pp 309–326

    Google Scholar 

  • Netz R (1999) The shaping of deduction in Greek mathematics: a study in cognitive history. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Norton JD (1996) Are thought experiments just what you thought? Can J Philos 26:333–366

    Article  Google Scholar 

  • Putnam H (1975) What is mathematical proof. In: H Putnam (ed) Mathematics, matter and method. Cambridge U.P. Cambridge, pp 60–78

  • Quine WVO (1951) Mathematical logic. Harvard University Press, Cambidge

    Book  Google Scholar 

  • Rav Y (2005) Reflections on the proliferous growth of mathematical concepts and tools: some case histories from mathematicians’ workshops. In: Cellucci C, Gillies D (eds) Mathematical reasoning and heuristics. King’s college publications, London, pp 49–69

    Google Scholar 

  • Rittberg CJ, Tanswell FS, Van Bendegem JP (2020) Epistemic injustice in mathematics. Synthese 197:3875–3904

    Article  Google Scholar 

  • Starikova I, Giaquinto M (2018) Thought experiments in mathematics. In: Stuart MT, Fehige Y, Brown JR (eds) The Routledge companion to thought experiments. Routledge, London, pp 257–278

    Google Scholar 

  • Stuart MT, Fehige Y, Brown JR (eds) (2018) The Routledge companion to thought experiments. Routledge, London

    Google Scholar 

  • van Bendegem J-P (1998) What, if anything, is an experiment in mathematics? In: Anapolitanos D, Baltas A, Tsinorema S (eds) Philosophy and the many faces of science. Rowman & Littlefield, London, pp 172–182

    Google Scholar 

  • van Bendegem J-P (2003) Thought experiments in mathematics: anything but proofs. Philosophica 72:9–33

    Google Scholar 

  • van Bendegem J-P (forthcoming) Experiments in mathematics: fact, fiction or the future?. In: Sriraman B (ed) Handbook of the history and philosophy of mathematical practice. Springer, Cham

  • von Koch H (1906) Une méthode géométrique élémentaire pour l’étude de certaines questions de la théorie des courbes planes. Acta Math 30:145–174

    Article  Google Scholar 

Download references

Acknowledgments

This article is a substantially revised and extended version of an old article published in Italian in 2009 in the journal Rivista di Estetica (Vol. 42(3), 39–54) that I presented at workshops in Paris, Nancy, Nice and Ghent. I thank the participants of all of them for their very useful comments, and in particular Margherita Arcangeli, Anouk Barberousse, Jean-Paul van Bendegem, Marco Buzzoni, Gerhard Heinzmann and Colin Rittberg. This work was supported by the Agence Nationale de la Recherche: Grant Number EUR FrontCog grant ANR-17-EURE-0017.

Funding

Funding was provided by Agence Nationale de la Recherche (Grant No. EUR FrontCog grant ANR-17-EURE-0017).

Author information

Authors and Affiliations

  1. Institut Jean Nicod, CNRS, Paris, France

    Valeria Giardino

Authors
  1. Valeria Giardino
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Valeria Giardino.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Giardino, V. Experimenting with Triangles. Axiomathes 32 (Suppl 1), 55–77 (2022). https://doi.org/10.1007/s10516-022-09639-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10516-022-09639-x

Keywords

Search

Navigation