Numerical Investigation of Regime Transition in Canopy Flows

Abstract

We have carried out highly resolved simulations of turbulent open channel flows. The channel wall is covered with different filamentous layers sharing the same thickness ($h=0.1H$, where H is the open channel height) and bulk Reynolds number (i.e., $Re_b=U_bH/\nu$, , $U_b$ is the bulk velocity and $\nu$ the kinematic fluid viscosity). The layers are composed of rigid, slender cylindrical filaments mounted perpendicular to the bottom wall. We have selected two layer configurations characterised by filament spacing ratios of $\Delta S/H=\pi /24\simeq 0.13$ and $\Delta S/H=\pi /32\simeq 0.098$. The geometrical features of the two layers, allow to classify them as transitional canopies ($\lambda =dh/\Delta S^2\simeq 0.15$, where d is the filament diameter, i.e. dh is the filament frontal area) (Monti et al. 2020), which is defined as the separation between the sparse-dense asymptotic regimes, proposed by Nepf (2012). While the physical characterisation of the two asymptotic regimes is fairly understood, the transitional conditions remain an open question since the physical characteristics unique to the sparse and dense scenarios coexist in the transitional regime. By resolving every single filament with the aid of an immersed boundary technique in the framework of a Large Eddy formulation, we report the physical mechanisms that emerge at the onset of different regimes (chosen values of $\lambda$ fall on the verge between a dense and a sparse condition) and verify the criterion associated with the inception of the transition regime.

1 Introduction

Canopy flows are commonly found in our surroundings, from natural environments to man-made urban areas (e.g. urban canopies). From a natural perspective, canopies can be generally associated with large terrestrial forests, wheat crop vegetation, and plants submerged in waterways. These substrates play an important role in creating a sustainable environment for living organisms to fulfil a number of vital tasks. Because of their significant contribution to complex phenomenological processes such as nutrient and light uptake, turbulent mixing, and sediment transport (Wilcock et al. 1999), vegetative canopies in rivers present an interesting case. Submerged canopy flows are often characterised by flow-plant interactions, that are able to trigger the onset of large-scale coherent structures, which influence both the momentum and scalar transport about and within the localised vegetative zones. Unravelling these dynamic physical mechanisms has the potential to bring about different technological advancements, including the alleviation of severe events such as flooding and contamination.

Fig. 1

Geometrical parameters that characterises an idealised canopy composed of cylindrical filaments(Nepf 2012), with $\Delta S$ h d and H representing the mean filament spacing, height diameter and open channel height respectively

The pioneering study by Ree and Palmer in 1949 (Ree and Palmer 1949) on the determination of the discharge rate in open channel flows bounded by an aquatic vegetative canopy, has established the inception and set the framework for subsequent investigations into canopy flows. The characterisation of canopy flows seems to be an almost impossible task, due to the existence of a large number of free parameters (i.e., distribution, density, height, and stiffness), let alone the presence of foliage and its reconfiguration). However, the recent contribution by Nepf and collaborators (Nepf 2012), proposing a classification encompassing a few geometrical parameters of the canopy (see Fig. 1) has opened new perspectives in the field. The classification recognises that for fully or partially submerged canopies, the flow behaviour approaches two limiting regimes depending on the value of the canopy solidity ($\lambda$), which is defined as $\lambda =\int _{0}^{h}a(y)dy$ , where y is the coordinate along the wall-normal direction and $a(y)=d(y)/\Delta S^2$, (refer to Fig. 1). If the value of $\lambda$ is much lower than a threshold ($\lambda<\!<0.1$) (the sparse regime), the mean velocity profile is analogous to the one of a rough wall boundary layer, since the drag offered by the canopy filaments is insignificant when compared with the frictional drag offered by the canopy bed. Conversely, if $\lambda>\!>0.1$, (dense regime) the drag imposed by the filamentous layer dominates the one of the canopy bed. This condition is characterised by an inflected mean velocity distribution, inducing a Kelvin-Helmholtz (KH) type instability at the tip of the canopy that presents an abrupt discontinuity in the drag profile. The KH-like instability may lead, through further non-linear stages, to the generation of large-scale structures presenting a large degree of coherence in the spanwise direction (Finnigan 2000). In this regime, the mean velocity profile exhibits two inflectional points, one invariably located at the canopy tip, and the second one residing near the canopy bed. Their existence indicates the emergence of two separated shear layers (Belcher et al. 2003), one related to the solid bed and the other to the external flow interface. Poggi et al. (2004) experiments investigating the effect of the canopy filament density on the surrounding flow have confirmed the aforementioned limiting scenarios. In particular, for canopies with $\lambda <0.04$, the authors observed the absence of a weak inflection at the canopy edge, with the mean velocity profile resembling a rough wall boundary layer. Conversely, when $\lambda >0.1$, the mean velocity profile featured the presence of two inflection points, in agreement with the classification proposed by Nepf (2012). Based on the experimental observations, the authors proposed a phenomenological model for the dense regime. In particular, the flow structure is idealised as a superposition of three different flow regions whose character is determined by the actual eddy size that the canopy layer can host. The first layer, termed the inner region ($y/h<\!<1$), is characterised by a von Kármán vortex street, with size and intensity highly dependent on the filament diameter and local Reynolds number. The outer layer ($y/h>2$) mimics a typical boundary layer that develops over a rough wall. However, the latter may be constrained in the context of shallow submerged canopies. Finally, the space by the canopy edge sandwiched between the innermost and outermost layers is characterised by a turbulent mixing layer, that is induced by the inflection point. The latter leads to the insurgence of a KH instability, which generates a mixing layer that rolls up, forming large-scale spanwise vortices. For a fully developed mixing layer, Raupach et al. (1996) observed that the streamwise wavelength ($\Lambda _x$) of the initial KH wavelength is preserved and the ratio $\Lambda _x/\delta _{\omega }$ (where $\delta _{\omega }=\Delta U/(\partial U/\partial y))$, is the vorticity thickness) falls in the range $3.5<\Lambda _x/\delta _{\omega }<5$. Motivated by the direct comparisons with a plane mixing layer, Raupach et al. (1996) observed that the ratio $\Lambda _x$ and the shear length scale ($L_s=U(h)/(\partial U/\partial y)_h \approx \frac{1}{2}\delta _{\omega }$) falls in a specific range of $7<\Lambda _x/\delta _{\omega }<10$, the validity of which was confirmed by compiling several experimental investigations. In the same context of densely submerged canopies, several authors proposed similar classifications of the canopy layer (Nezu and Sanjou 2008; Monti et al. 2020). Aside from the inflectional point characterised at the filament tip, a recent numerical study by Monti et al. (2020) reported the occurrence of a further inflectional point that lies deep inside the canopy. The latter is probably generated by the merging of the outer velocity profile with the distribution by the canopy bed. In particular, the inflection point triggers a spanwise modulation of the streamwise velocity fluctuations. This modulation is fed by the large sweep and ejection events of the outer flow that diverge into the stream- and spanwise fluctuation as a consequence of the coupling between impermeable wall conditions and incompressibility.

So far, the majority of the work accumulated on canopy flow has been limited to experiments (Poggi et al. 2004; Ghisalberti and Nepf 2009) and a few simplified simulations based on a homogenised drag model (Cui and Neary 2008; Zampogna and Bottaro 2016). However, the recent increase in computational power and the availability of novel immersed boundary formulations, have provided the framework for the insurgence of high fidelity canopy flow simulations (Monti et al. 2019; Sharma and García-Mayoral 2020). In the used formulations, the authors by enforcing the boundary condition on every single filament, were able to capture the essential dynamics of the flow that develops within the canopy layer and shed some light on the physics mechanisms that emerge at the onset of the different flow regimes. Although some promising results were obtained, this still remains an open area of research, with the available literature covering a limited number of configurations. In particular, the so-called transitional regime that exists in between the two asymptotic regimes (i.e., sparse and dense) (Nepf 2012) remains an uncharted territory, as the flow field is characterised by a complex transition from a rough-wall like behaviour to canonical mixing layer flows. Furthermore, the interplay between the various localised layers that exist within the canopy and their thicknesses in the transitional regime still needs complete characterisations.

In the present study, we have conducted a series of highly resolved simulations of open-channel turbulent flows, where the bottom impermeable wall is covered by a canopy of cylindrical rigid filaments. The boundary condition (zero velocity) was enforced on every single filament with the aid of a state-of-the-art immersed boundary formulation. Different to the previous work by Monti et al. (2020), the selected configurations share the same level of submergence (i.e., $H/h=10$) and have been obtained by modulating the average distance between adjacent filaments ($\Delta S$) (i.e. the density of the filaments), such that the corresponding value of $\lambda$ nominally falls in the transitional regime.

2 Numerical Technique

The high fidelity numerical simulations of turbulent flows developing above rigid canopies was conducted using SUSA, an in-house developed, incompressible Navier-Stokes solver (Omidyeganeh and Piomelli 2013; Monti et al. 2019). In particular, the outer flow is dealt with a large eddy formulation, in which the governing Eqs. 1 and 2 are determined by filtering out the velocity and pressure fluctuations that take place below a spatial filter width falling in the inertial sub-range of turbulence.

$$\begin{aligned}&\displaystyle \frac{\partial \overline{u}_{i}}{\partial x_i}=0 \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \frac{\partial \overline{u}_i}{\partial t} + \frac{\partial \overline{u}_i \overline{u}_j}{\partial x_j} = -\frac{\partial \overline{P}}{\partial x_i} + \frac{1}{Re_b} \frac{\partial ^2 \overline{u}_i}{\partial x_j x_j} - \frac{\partial \tau _{i,j}}{\partial x_{j}} + f_i \end{aligned}$$

(2)

In particular, the sub-grid scale Reynolds stress tensor ($\tau _{i,j}=\overline{u_{i}u_{j}}-\bar{u_i}\bar{u_j}$), resulting from the filtering operation, was modelled using an eddy viscosity based, Integral Length Scale Approximation (ILSA) approach, which was originally proposed by Piomelli et al. (2015). The resulting unresolved stresses are modelled as,

$$\begin{aligned} \displaystyle \tau _{i,j}-\frac{\delta _{i,j}}{3}\tau _{k,k}=-2\nu _{sgs}\overline{S}_{i,j} \end{aligned}$$

(3)

where $\overline{S}_{i,j}$ is the resolved strain rate tensor and $\nu _{sgs}$ is the eddy viscosity. In the adopted ILSA model, the latter is determined by $\nu _{sgs}=(C_k L)^2 |\overline{S}_{i,j}|$, where $C_k$ is the model constant and L is the integral length scale. The corresponding length scale is determined by considering the turbulent kinetic energy of the resolved scale and the total dissipation rate. The length scale and the model constant required by the model closure is computed locally and instantaneously, thus eliminating any dependence on the Eulerian grid (Rouhi et al. 2016). The inner region of the canopy flow, automatically switches to a direct simulation because of the local grid size and the features of the adopted Large Eddy Simulation (LES) closure model’s sub-grid scale activity inside and outside the canopy layer, will be discussed later.

SUSA employs a spatial discretisation of the incompressible LES equations based on a second-order accurate, cell-centered co-located finite volume formulation on a structured grid. The computational grid nodes for the velocity components ($u_i$) and pressure (p) are co-located at the cell centre and the appearance of the well-known spurious oscillations is avoided by employing a deferred correction following the approach proposed by Rhie and Chow (1983). The governing equations are advanced in time, using a second order, semi-implicit fractional step procedure (Kim and Moin 1985). In particular, a second order accurate, explicit Adam Bashfort scheme is applied to the non-linear and wall parallel diffusive terms, while the wall-normal diffusive terms are treated with a second order accurate, implicit Crank Nicolson scheme. The Poisson pressure equation, which is solved at each time step to satisfy the continuity constraint, is transformed into a series of one-dimensional (1-D) equations in the wavenumber space via an efficient multi-dimensional Fast Fourier Transform (FFT) (Dalcin et al. 2019). Each transformed equation is solved directly using Cholesky’s factorisation technique. Adopting a domain decomposition technique, the code is parallelised using the Message Passing Interface (MPI) library. Further details on the code, its parallelisation and the extensive validation campaign, that has been carried out for other flow configurations can be found in previous publications: (Omidyeganeh and Piomelli 2011, 2013; Rosti et al. 2016).

Table 1 Simulation parameters considered in the current investigation

The mean filament spacing and the height can be set to match any wanted solidity value ($\lambda$), thus selecting different nominal regimes of the canopy flow. In the present study, we focus on the transitional regime and the values of $\lambda$ corresponding to the two canopies were obtained by maintaining a constant filament height (h) and diameter (d), whilst modulating the in-plane solidity ($\Delta S$) to match the transitional criterion $\lambda \approx 0.15$ and $\Delta S/h\simeq 1$ (Monti et al. 2020). The chosen $\Delta S$ values lead to two canopy configurations corresponding to $\lambda \in [0.14, 0.25]$ and $\Delta S/h \in [1.31, 0.98]$ (see Table 1). As mentioned, the zero velocity condition is enforced stem-by-stem using an Immersed Boundary formulation (IBM) described in Pinelli et al. (2010). Each filament has a finite, circular cross-sectional area and is discretised using a set of Lagrangian nodes distributed along the filament in the wall-normal direction. The nodes discretising the filament do not need to conform to the underlying Eulerian grid. More specifically, a compact support defining the cross-sectional size of each rod is centred around each Lagrangian node and the body force required to enforce the Dirichlet type boundary condition is computed and spread on each support as a part of the time-advancing scheme (Pinelli et al. 2010). The dimension of this compact support depends on the local grid size and defines the hydrodynamic thickness (i.e., the diameter) of the filament. In the current numerical set-up, using a uniform grid in the wall parallel directions, the thickness of each filament is estimated to be of about $d \approx 2.2 \Delta x_i$ ($\Delta x_i$ being the grid size in the streamwise and spanwise directions) (Monti et al. 2019). Further details on the adopted IBM, its properties and implementation are extensively described and discussed for various flow configurations in Pinelli et al. (2010) Favier et al. (2014), while the IBM assessment in the context of canopy flows, including its calibration of the support cage required to deliver the desired resolution and its extensive validation campaign, is described and discussed in (Monti et al. 2019). Concerning the distribution of the filaments in the canopy substrate, we have used a tiled approach, in which the bottom impermeable wall is meshed into square tiles of size $\Delta S/H$. Each tile holds a single filament, and its local position on each individual tile is assigned randomly according to a uniform probability distribution. This approach prevents the introduction of specific patterns that may promote flow channelling effects within the voids between neighbouring filaments.

Fig. 2

a Ratio of the sub-grid scale energy to the total fluctuating energy as a function of the wall normal direction b Ratio between eddy viscosity and the physical viscosity along the wall normal direction. The parameters have been averaged both in space (i.e., homogenous directions) and time

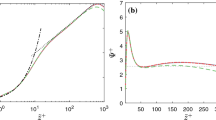
Concerning the overall LES filter operator, the adopted ILSA model enables the computation of a dynamic yet localised eddy viscosity. In this condition, the external flow in the region outside the canopy can be considered as a coarse Direct Numerical Simulation (DNS), that progressively becomes highly resolved when approaching the canopy layer. In particular, the primary role played by the sub-grid scale stresses in the outer region is limited to a very mild and stabilising numerical dissipation (Monti et al. 2020). Figure 2a illustrates the ratio between the sub-grid scale and total energies averaged in time and in the wall-parallel directions, as a function of the wall-normal direction. It is clearly evident that this ratio is always below $10^{-5}$ for all the canopy configurations considered in the current investigation. Further insight into the LES filter activity can be obtained by inspecting Fig. 2b, which presents the ratio between the eddy viscosity and the physical one, as a function of the wall-normal distance. The parameter averaged both in space and time, is always less than one ($<1$) for the whole domain, illustrating clearly that the LES filter operates at the end of the turbulence cascade. This posterior analysis suggests that any adjustments associated with the coupling between the LES and the IBM can be negated.

The two canopy simulations share the same computational box, with the streamwise length, open channel depth H and spanwise width corresponding to $L_x/H=2\pi$, $L_y/H=1$ and $L_z/H=1.5\pi$, respectively. To mimic an open channel, we have enforced no slip (i.e., zero velocity) and a freeslip (i.e., $\partial _yu=\partial _yw=0, v=0$) conditions on the bottom wall and on the top surface, respectively. The homogeneous directions (i.e., streamwise and spanwise), are treated with periodic boundary conditions. Concerning the features of the numerical grid, we have employed a stretched distribution based on a tangent hyperbolic function in the wall-normal direction. At every time step, a uniform pressure gradient is modulated, such that a constant, time-independent volumetric flow rate is attained, which corresponds to the bulk Reynolds number of $Re_b=U_bH/\nu =6000$. This choice aligns with other numerical (Monti et al. 2020) and experimental (Ghisalberti and Nepf 2004) investigations. The numerical grid resolution of all the cases, based on the outer friction scales (i.e. friction velocity computed at the virtual origin of the outer flow) satisfies the standard DNS thresholds (i.e., $\Delta x^+=\Delta z^+\le 9, \Delta y^+\le 0.4$). Moreover, the adequacy of the grid has been assessed using a preliminary grid convergence study discussed in Monti et al. (2020).

3 Results and Discussion

In this section, we present the results obtained from statistically converged simulations of the two considered TS and TD canopy configurations. All the figures incorporate results from both canopy configurations: TS results were represented using red lines and the TD case represented blue lines, respectively. For comparison, we have also incorporated the results of the canonical smooth wall turbulent channel flow at $Re_\tau =950$ (Hoyas and Jiménez 2008), which are represented by black lines.

We start to review the results by considering the mean velocity distribution scaled with the open channel height (H) and the bulk velocity ($U_b=\frac{1}{H}\int _0^H\langle U \rangle dy$, where the $\langle . \rangle$, is an operator indicating averaging in both time and homogenous directions). The distributions in Fig. 3, clearly exhibit the existence of two inflectional points, located at the canopy edge (outer) and within the canopy layer (inner), with the location of the latter highly dependent on the actual canopy flow regime (Monti et al. 2020). The outermost inflectional point is induced by the abrupt discontinuity of the drag force at the canopy tip, whilst the internal one is a result of the merging of the mean flow developing by the wall with the velocity distribution underneath the canopy tip (Monti et al. 2019). The mean locations of the two inflectional points can be estimated by considering the mean momentum balance in the streamwise direction.

$$\begin{aligned} \frac{1}{Re_b}\frac{\partial ^2 \langle U \rangle }{\partial y^2}=\frac{\partial P}{\partial x}+\frac{\partial \langle u'v'\rangle }{\partial y}+ \langle F_D\rangle \end{aligned}$$

(4)

The first three terms in Eq. 4, represent the mean viscous force, mean streamwise pressure gradient and the mean Reynolds shear stress, respectively. The last term represents the contribution of the overall mean drag imposed by the individual filaments of the canopy. In particular, the mean wall-normal location of the inflection points is determined when $\partial ^2 \langle U \rangle /\partial y^2=0$ is satisfied. Their positions within the canopy are represented by the circles in Fig. 3a.

Fig. 3

Mean velocity profiles a in terms of the outer flow units (i.e., H and $U_b$). The circle symbols presents the mean locations of the internal inflection point and dashed lines represents the virtual origin. The black horizontal line represents the canopy height (h), while the dashed lines represents the position of the virtual origin (see text for definition) b in terms of the wall units. The $\tilde{y}^+$ represents the wall normal coordinates made non-dimensional with the inner and outer wall units, based on their origin. See text for colour-band and description on the virtual origin

The internal and external boundary layers are illustrated in Fig. 3b. To characterise the inner flow, we use the friction velocity $u_{\tau ,in}=\sqrt{\tau _{w}/\rho }$, based on the wall shear stress at the canopy bed. The profiles exhibit behaviour that matches the typical velocity profile of a canonical turbulent channel flow (Hoyas and Jiménez 2008). However, this is only limited to the viscous sub-layer, where the skin frictional drag dominates the drag imposed by the filaments (Monti et al. 2020). Moving away from the wall, we observe the modification of the buffer layer generated by the presence of the stems. In particular, this region is dominated by the filament-induced, meandering motion and the alternating upwash and downwash movements driven by the outer flow. In the tip region, we define an external friction velocity based on the total stress evaluated at the virtual origin ($y_{vo}$). This can be interpreted as the virtual location of an abstract wall seen by the outer turbulent boundary layer that develops above the canopy, which is assumed to obey the “displaced” logarithmic law (Jiménez 2004). We compute the wall-normal position of $y_{vo}$ implicitly, by enforcing the canonical velocity log law on the outer layer mean velocity profile,

$$\begin{aligned} \frac{\langle U \rangle }{u_{\tau ,o}}=\frac{1}{\kappa }log\left( \frac{(y-y_{vo})u_{\tau ,o}}{\nu } \right) +B -\Delta U^+ \end{aligned}$$

(5)

where $y-y_{vo}$ is the shifted wall normal coordinates for the outer flow. $u_{\tau ,o}^2=\partial _y U_{vo} - u'v'_{vo}$ is the outer (global) friction velocity computed at the virtual origin, $\kappa$ is the von Kármán constant here set at 0.41 and B is the intercept in a smooth wall configuration. Figure 3b reveals a standard turbulent boundary layer logarithmic profile, with a downward shift ($\Delta U^+$), suggesting that the canopy exhibits a rough-wall-like behaviour for the outer flow. In the context of rough wall boundary layers, the term $\Delta U^+$ is often, termed as the roughness function (Hama 1954). The universality of the logarithmic layer has been previously reported by other authors (Mizuno and Jiménez 2013; Kwon and Jiménez 2021). In particular, (Kwon and Jiménez 2021), conducted a novel experiment by isolating the multi-scale dynamics of the logarithmic region, which showed a robust and uniform behaviour of the flow structure regardless of the imposed manipulations.

The features of the mean velocity profile and their locations within the canopy, allow us to identify three localised layers: an inner layer, developing between the canopy bed and the inner inflection point; an outer layer spanning the region from the canopy tip down to the position of the virtual origin and lastly, an overlap region sandwiched in-between them. The latter is home to complex interactions between the internal and external boundary layers. The existence of the overlap region depends on the actual canopy regime. In the TS configuration, the virtual origin has penetrated the inner layer (i.e., below the internal inflection point), resulting in the absence of an overlap layer, indicating a strong interaction between the inner and outer layers. However, the virtual origin of the TD configuration has moved away from the canopy bed and is located just above the inner inflectional point. The location of the latter, in turn, has moved towards the wall, when compared with the TS case, thereby inducing an overlap layer of marginal thickness. Moreover, decreasing the mean filament spacing ($\Delta S$) below the value used for the TD configuration may result in an increase in the thickness of the overlap layer. However, this would represent the inception of a dense canopy flow regime, which is beyond the scope of the current study. From Figs. 3a and 4, it is evident that the mutual signed distance between the two points has a zero in between the TS and TD configurations (i.e., $0.14< \lambda < 0.25$). By performing a simple linear interpolation, we find that zero corresponds to $\lambda =0.21$, which is close to the value identified as a possible criterion to establish the inception of the dense regime (Monti et al. 2020). It should be noted that the proposed classification is associated with pressure-driven flows and may not be applicable to canopy flows that concerns with zero-pressure gradient boundary layers, which is outside the scope of the current work (Zhang et al. 2022).

Fig. 4

Mean locations of the mean velocity features, revealing the extent of the localised layers embedded within the canopy. The dashed and solid horizontal lines represents the locations of the internal inflection and virtual origin, respectively

Fig. 5

Velocity fluctuations distributions made non-dimensional with the outer friction velocity ($u_{\tau ,o}$). The solid, dashed and dotted lines represents the streamwise, wall normal and spanwise components. See text for colour-band

Figure 5, presents the diagonal Reynolds stress distributions, made non-dimensional with the outer friction velocity ($u_{\tau ,o}$), as a function of the wall-normal distance scaled with the open channel height (H). Away from the canopy, the stress profiles resemble the canonical smooth wall turbulent channel, confirming the outer layer similarity (Townsend 1976). Overall a good collapse can be observed, apart from the region close to the upper boundary $y/H=1$, where the differences between an open vs full channel persist. This behaviour was similarly reported by Scotti (2006) where the authors analysed turbulent open channel flows developing over transitionally rough surfaces. However, deep inside the canopy, we observe a behaviour highly dependent on the selected canopy configuration. In particular, the streamwise and spanwise components have been dampened by the increased filament number density, while the wall-normal components remain unaffected. Nevertheless, both configurations share the same outer peak intensity for all three components. This indicates there is a need for better scaling in the inner region of the canopy, which would enable us to make a direct comparison of the velocity r.m.s fluctuations. To this end, we consider the integral form of the mean momentum balance (see Eq. 4) from an arbitrary y location up to the free shear surface of the open channel (i.e., $y=H$).

$$\begin{aligned} \left( 1-\frac{y}{H}\right) \left| \frac{\partial P}{\partial x}\right| H =\mu \frac{\partial \langle U \rangle }{\partial y}-{ \langle u'v'\rangle }-\int _y^H\langle F_D\rangle \end{aligned}$$

(6)

where $\left| \frac{\partial P}{\partial x}\right|$ represents the absolute value of the mean pressure gradient used to drive flow at a constant flow rate. If the lower limit of the integral is replaced by the location of the canopy bed (i.e., $y=0$), the balance equation reads as,

$$\begin{aligned} \left| \frac{\partial P}{\partial x}\right| H =\tau _{w}+\int _0^H\langle F_D\rangle \end{aligned}$$

(7)

Fig. 6

a Mean momentum balance, with solid, dashed, and dotted lines representing the viscous, Reynolds stress, and the cumulative drag contributions. The solid black line represents the norm of the average pressure gradient. b Viscous and Reynolds stresses re-scaled with the local friction velocity $u_{\tau ,l}$

where $\tau _w$ is the wall shear stress and $\int _0^H\langle F_D\rangle$ is the cumulative drag contribution and the left-hand-side term represents the norm of the mean pressure gradient. The respective contributions of all the terms appearing in the balance Eq. 6 are reported in Fig. 6a. Outside the canopy, the cumulative drag term is zero and the distributions of the viscous and Reynolds stress contributions are similar to those of a smooth wall. Recently, Monti et al. (2019) and Sharma and García-Mayoral (2020) studied mildly dense and sparse canopies, respectively observing that the scale of the turbulent fluctuations well with the local total stress, defined as the sum of the viscous and Reynolds stresses. In the current framework, we aim to extend this scaling argument to canopies that fall in the transitional regime, by defining a local friction velocity scale based on the total stresses as,

$$\begin{aligned} u_{\tau ,l} = \sqrt{\frac{H}{H-y}\tau (y)} = \sqrt{\frac{\mu {\partial _y \langle U \rangle } - \langle u'v'\rangle }{1- y/H}} \end{aligned}$$

(8)

This local scaling yields a non-dimensional linear variation of the total stress when scaled with the local friction velocity. The local friction velocity formulation has also been quite successful in the context of artificially manipulated shear flows, although the total stress did not exhibit a linear variation with the wall normal direction (Jiménez 2013; Tuerke and Jiménez 2013).

Fig. 7

a Velocity and b vorticity fluctuations distributions rescaled with the local friction velocity scale ($u_{\tau ,l}$) and the open channel height (H). The solid, dashed and dotted lines represents the streamwise, wall normal and spanwise components. See text for colour-band

Figure 7a, displays the diagonal terms of the Reynolds stress tensor rescaled with the local friction velocity defined in Eq. 8. In particular, we observe two peaks located in the inner and outer regions of the canopy. The distribution of the stresses outside the canopy once again confirms the negligible role played by the imposed wall conditions on the external flow structures (Scotti 2006). The behaviour of the wall parallel components in the inner layer indicates the impact of the canopy on the velocity fluctuations, which takes the form of an intensification of the spanwise component and a weakening of its streamwise counterpart. This behaviour appears quite clearly when considering the TD configuration, suggesting the existence of a redistribution mechanism for the velocity fluctuations induced by the presence of the filaments. These act as obstacles and disrupt the streamwise coherence of the inner flow. The role played by the stems is further confirmed by the distribution of the wall-normal component of the velocity fluctuations. The mild deficiency of the proposed scaling in the vicinity of the canopy edge can be attributed to the imbalance between production and dissipation induced by the abrupt change in the drag profile (Monti et al. 2019). In Fig. 7b, we present the vorticity fluctuations that have been normalised by the local friction velocity (see Eq. 8) and open channel height (H). The intensity of all three components has substantially increased, across the canopy layer. An interesting behaviour can be observed for the wall-normal component ($\omega _{y,rms}^+$). In particular, the peak for the TS configuration presents an outward shift, when compared with the smooth wall profiles, similar to a rough wall boundary layer (Abderrahaman-Elena et al. 2019). However, the corresponding peak of the TD configuration presents an inward shift relative to the TS configuration, indicating a departure from the rough-wall-like behaviour. It is noted that the peak locations are highly influenced by the alternating spanwise velocity fluctuations along the streamwise direction, induced by the presence of the filaments.

Fig. 8

Distributions of the velocity fluctuations a,c and the stresses as a function of the non-stretched (top row) and stretched (bottom row) viscous units. The solid, dashed and dotted lines in the first columb represents the streamwise, wall normal and spanwise components. The solid and dashed lines in the second column represents the viscous and Reynolds stresses. See text for colour-band

Before moving into the analysis of the higher dimensional statistics, we discuss the appropriateness of the chosen viscous length scale. Based on the local friction velocity formulation presented in Eq. 8, we define a local viscous unit as, $\delta _{\nu ,l} = \nu /u_{\tau ,l}$. In Fig. 8a and b, we present the profiles of the velocity fluctuations and the stresses versus the local viscous units (i.e., $y_{l}^{+}=y/\delta _{\nu ,l}$). While there is a good collapse of the profiles away from the wall, the same cannot be said for the inner region of the canopy. This can be attributed to the several geometrical length scales introduced by the canopy, e.g. average filament spacing ($\Delta S$), height (h), filament diameter (d), mean positions of the virtual origin and the internal inflection point and their signed distances. In the spirit of adopting the proposed scaling to the conditions of the canopy, we employ a non-dimensional stretching factor ($\alpha$) suggested by Monti et al. (2020). Different from their choice, we select the aspect ratio ($\Delta S/h$), which is the most relevant length scale of the canopy regime under scrutiny (Monti et al. 2020; Sharma and García-Mayoral 2020). The resulting, stretched viscous unit takes on the definition:

$$\begin{aligned} y_{\alpha }^{+} = \frac{1}{\alpha }\frac{u_{\tau ,l}y}{\nu }=\frac{h}{\Delta S}\frac{u_{\tau ,l}y}{\nu } \end{aligned}$$

(9)

The robustness of the proposed scaling can be easily seen in Fig. 8c and d, where the profiles exhibit a good collapse for the two configurations. From a physical perspective, in the sparser regime, the turbulent eddies of the external boundary layer can easily penetrate the full extent of the canopy since the penetration of the external vortices is only constrained by the distance to the wall (i.e., h). However, as the canopy becomes denser, the interaction with the outer flow weakens and only characteristic vortices with size $\Delta S$ are able to penetrate the canopy. Therefore, it is reasonable to incorporate the proposed aspect ratio into the definition 9.

To obtain further insight into the emergence and organisation of the large coherent structure prevalent in both the internal and external boundary layers, we turn our attention to the fluctuating velocity field. Following (Nikora et al. 2007) and (Mignot et al. 2009), we introduce a double averaging technique to decompose an instantaneous flow quantity ($\phi$),

$$\begin{aligned} \phi (x,y,z,t) = \langle \bar{\phi } \rangle (y) + \tilde{\phi }(x,y,z) + \phi ^{\prime }(x,y,z,t) \end{aligned}$$

(10)

into a space-time mean quantity ($\langle \bar{\phi } \rangle$), spatial fluctuation of the temporal average ($\tilde{\phi }$) and the full turbulent fluctuation ($\phi ^{\prime }$). The term $\tilde{\phi }$, which is computed from the time-averaged flow field (i.e., $\tilde{\phi }=\bar{\phi }(x,y,z)-\langle \bar{\phi } \rangle (y)$), is also known as the dispersive component. The usefulness of this triple decomposition mainly concerns the filamentous layer, since the canonical Reynolds decomposition is recovered (because the dispersive terms tend to zero), in the region outside the canopy. This is clearly seen in Fig. 9, where the form-induced (dispersive) stresses are presented as a function of the wall-normal distance scaled with the filament height. The figure illustrates the streamwise ($u_{d}^{\prime }$ ), wall-normal ($v_{d}^{\prime }$ ) and spanwise ($w_{d}^{\prime }$) and the anisotropic ($u_{d}^{\prime } v_{d}^{\prime }$) components of the dispersive stresses. These stresses are often neglected in the context of canopy flows, however, they play an important role in the momentum transfer within the canopy, especially in the sparse and transitional regimes (Poggi et al. 2004). Consistent with previous rough-wall studies (Mignot et al. 2009; Yuan and Piomelli 2014), the wall-normal and spanwise components in Fig. 9 have a lower intensity relative to the corresponding streamwise component. Apart from the latter, which is comparable to the Reynolds stresses, the form-induced stress profiles for both canopy configurations agree well with each other. In particular, the magnitude of the $u_{d}^{\prime }$ peak for the TD case has decreased, in agreement with the behaviour observed by Poggi et al. (2004).

Fig. 9

Form induced dispersive stresses as a function of wall normal distance normalised with the canopy height. The solid, dashed and dotted lines represents the streamwise, wall normal and spanwise components, while the symbols represents the anisotropic term ($u_d^{\prime }v_{d}^{\prime }$). See text for colour-band

Fig. 10

Wall parallel instantaneous snapshots located at $y/H=0.02$ a, b, e, f and at $y/H=0.15$ c, d, g, h. The columns from left to right represents the streamwise and spanwise fluctuations, respectively ($u^{\prime +}, w^{\prime +} \in [-4,4]$). The rows from top to bottom represents the TS (first and second) and TD (third and fourth) configurations, respectively

The presence of the filamentous layer induces a meandering motion, amplifying the signature of the spanwise velocity fluctuation within the canopy. The instantaneous velocity fluctuations ($u^{\prime }$ and $w^{\prime }$) presented in Fig. 10, have been sampled at two wall parallel planes locations, one deep inside the canopy and the other in the vicinity of the canopy tip. In particular, Figs. 10a, b, e and f clearly illustrate the sinuous deviation of the flow in the intra-canopy region, due to the presence of the filaments and its eventual contribution towards the spanwise velocity fluctuations. Furthermore, the intra-canopy flow also inherits a footprint of the quasi-streamwise vortices that populate the external flow, which can be attributed to the negligible or very mild decouple between the inner and outer flow in the transitional regime. A close examination of the streamwise component of the TD configuration reveals an interesting feature. In particular, Fig. 10e, contains the weak traces of a spanwise coherent motion, resembling the Kelvin Helmholtz instability that is typically found in dense canopies. The spanwise modulation of the streamwise velocity fluctuation deep inside the canopy was originally reported by Monti et al. (2020), in the context of the fully dense regime.

Fig. 11

Pre-multiplied spectra of the velocity fluctuations, as a function of the wall normal distance and the streamwise (top row) and spanwise wavelength (bottom row) scaled with the outer units. The first, second and third columns represents the streamwise, wall normal and spanwise components, respectively. The short vertical lines presents the wavelength of the mean filament spacing corresponding to the two canopy configurations, while the black line represents the wavelength equivalent of filament diameter

The organisation of the coherent structures observed in the instantaneous snapshots can be further analysed by, considering the spectral energy content. To this end, the pre-multiplied spectra of the fluctuating velocity components are presented in Fig. 11, as a function of the wall-normal distance (y/H) and wavelengths along both homogeneous directions (i.e. streamwise $\lambda _x/H$ and spanwise $\lambda _z/H$). The panels in Fig. 11, reveal the presence of two primary fluctuating peaks located in the inner and outer regions of the canopy for both configurations. Concerning the internal maxima in the canopy layer (i.e., $y/H\le 0.1$), we observe its occurrence at three wavelengths. In particular, the left-most peaks, occurring at short wavelengths, are comparable to the geometrical length scales of the canopy, including the filament diameter and spacing (i.e., $\lambda _x, \lambda _z= [d, \Delta S]H$). This can be associated with an obstacle-induced, flow deviation and the formation of a wake behind each filament. In Fig. 12, we present pre-multiplied spectra as function of the $\lambda _x$ and $\lambda _z$ wavelengths, at three wall-normal locations that corresponds to the inner region ($y=0.02H$), the canopy edge ($y/H=h$) and the outer region ($y/H=0.15$). The right-most peak of $u^{\prime }$ and $w^{\prime }$ in Fig. 11, which is comparable with Fig. 12, corresponds to the large wavelength, typically of the order $\lambda _x, \lambda _z \sim \mathcal {O}(H)$. This extremum can be associated with the large-scale structures of the outer flow that preferentially penetrate the canopy through the wall-normal component, similarly observed in the instantaneous planar snapshots offered in Fig. 10. A closer examination of panel a in Fig. 12 reveals an interesting behaviour of the pre-multiplied spectra of the streamwise component. First, the extent of the maxima corresponding to large wavelengths has decreased relative to the TS configuration, indicating a weaker footprint of the outer logarithmic structures deep inside the canopy. This can also be clearly seen in the pre-multiplied spectrum of the $v'$ (see panel b of Fig. 12). Second, the spectra of $u'$ of the TD case, highlight the presence of a peak at wavelength $\lambda _x=0.5H$ and $\lambda _z=H$, with the streamwise wavelength similar to the distance from the canopy bed to the inner inflection point. The association of the respective maxima with the large-scale wavelengths, suggests the emergence of a different physical mechanism that would be responsible for its inception. When focusing on the instantaneous snapshots (panels e and f in Fig. 10) and the spectral decomposition (panels a and c in Fig. 12), we indeed observe the signature of a new coherent motion embedded in the background of large scale structures. In particular, the $u^{\prime }$ is organised with a spanwise coherency, while the $w^{\prime }$ is more organised along the diagonal direction. The panels extracted at the canopy edge and the outer flow clearly illustrate that the observed flow structure progressively vanishes when moving away from the wall, indicating a partial decoupling of the inner and outer flows.

Fig. 12

Pre-multiplied spectra of the velocity fluctuations, as a function of the streamwise and spanwise wavelength scaled with the outer units. The three rows (top to bottom) corresponds to three wall normal locations $y=0.02H, h, 0.15H$. Panels a, d and f, b, e and h and c, f and i, represents the streamwise, wall normal and spanwise components, respectively. See Fig. 11 for the definitions of the colour lines

Next, we discuss the insurgence of the peak observed in the outer region. To deepen the discussion, we also consider the co-spectra shown in Fig. 13. All the panels of Fig. 11 and the bottom row of Fig. 12, reveal the existence of a maximum associated with a large spatial scale. In particular, the external maxima of $u^{\prime }$ corresponds to a very long streamwise wavelength with a modulation in the spanwise direction (see panels a and d of Fig. 11). These outer large-scale structures are characterised by velocity streaks that are typically found in the logarithmic region in wall-bounded flows (Jiménez 2013). Moreover, the peaks of $v^{\prime }$ and $w^{\prime }$ detected just above the canopy in panels e and f of Fig. 11, confirm the presence of quasi-streamwise vortices that flank large scale streaky structures. The occurrence of these vorticity structures is clearly evident in the instantaneous iso-surfaces of the streamwise velocity fluctuations, presented in Fig. 14. Apart from the typical logarithmic structures, the occurrence of a set of spanwise rollers in the context of canopies that fall into the transitional regime still remains an open question. When dealing with dense canopies, the inflection point of the mean velocity is known to trigger a KH-like instability that leads to the formation of large-scale spanwise coherent rollers. It should be noted that these rollers are not well-defined vorticity structures, which can be easily detected (Finnigan et al. 2009) through snapshots. However, the wall-normal velocity fluctuation is a good indicator of the presence of these vorticity rollers (Sharma and García-Mayoral 2020). This is the case for the two-dimensional pre-multiplied spectra of the $v'$ extracted at the canopy edge (see panel e of Fig. 12) from where we observe a spanwise coherent spectral peak occurring within a narrow streamwise wavelength band, for both canopy configurations. Alternatively, the emergence of the set of spanwise rollers centred around the edge of the canopy can be detected by the outer peaks of the one-dimensional pre-multiplied co-spectra of the Reynolds stress, as shown in Fig. 13. Another indication of the presence of the rollers can be evinced by the streamlines drawn on the lateral plane of Fig. 14, which have been obtained by averaging the velocity fluctuations along the spanwise direction. The occurrence of such spanwise oriented vorticity structures has been previously reported by other authors in the context of porous substrates (Jimenez et al. 2001; Rosti et al. 2018).

Fig. 13

Magnitude of the pre-multiplied co-spectra of the $u'v'$ as a function of the wall normal direction scaled in outer units. The left and right panels represents the dependence on the streamwise ($\lambda _{x}/H$) and spanwise ($\lambda _{z}/H$) wavelength, respectively. See Fig. 11 for the definitions of the colour lines

4 Conclusions

In the present work, we have investigated the turbulent flow that develops above a rigid filamentous surface in the framework of the so-called transitional regime. Two canopy configurations that nominally fall into this regime were selected. Differently from previous investigations that were focusing on the frontal area (i.e. the canopy height), the solidity $\lambda$ has been modified solely by decreasing the average distance between the adjacent filaments (or increasing the stem number density), yielding configurations residing above and below the sharp transitional threshold (i.e., $\lambda \simeq 0.15$) (Monti et al. 2020). The main conclusions of our work can be summarised as follows.

Firstly, we have confirmed the occurrence of a regime transition occurring within the range bounded by the two considered configurations. The signature of such transition is identified as in Monti et al. (2020) by the signed distance between the internal inflectional point and the virtual origin occurring when the canopy aspect ratio is unity (i.e., $\Delta S \approx h$). In this condition, we have shown the mean position of the internal inflection point and the virtual collapse onto a single location ($y_{vo},y_{inf} \simeq 0.5h$), dividing the canopy into two layers. This induces a decouple between the innermost and outermost boundary layers, whose interactions are limited to the sweep and ejections generated by the outer flow via the wall-normal component. This outer/inner communication weakens as the average filament spacing is further decreased (or equivalently increasing solidity), enhancing a stronger decoupling in the limiting condition $\Delta S \rightarrow 0$. The exploration of this limiting condition is still underway. Secondly, we have identified and characterised the flow topology across the whole canopy flow in the transitional regime. This area is dominated by large-scale structures, and to the author’s knowledge, this is the first time, that the presence and the character of these structures in a transitional regime have been put forward with conclusive and quantitative evidence across the canopy layers. The analysis has been mainly conducted by looking at the spectral energy content of the velocity fluctuations, allowing us to identify the different structures of the velocity fields, particularly in the region bounded by the canopy. In particular, we have reported the existence of a spanwise modulation of the streamwise velocity fluctuations hidden in the background of larger energetic structures, triggered by the innermost inflection point. Previously, this phenomenon unique to the fully dense scenario was only reported for a single canopy configuration ($\lambda =0.56$) (Monti et al. 2020). Its weak inception at a relatively low value of $\lambda$, establishes the importance of $\Delta S$ as the primary length scale that governs the interaction between the inner and outer boundary layers and eventually the transition between two asymptotic regimes.

Concerning the structure of the external boundary layer developing over a transitional canopy, this is characterised by highly elongated velocity streaks bound by intense quasi-streamwise vortices. The outer layer is also home to a system of spanwise oriented vorticity structures in the form of a Kelvin Helmholtz type instability that emerges as a result of the inflected mean velocity profile. These large structures have been previously reported by several other authors, in the context of obstructed flows (i.e., dense canopy flows, flows over porous media, and roughness elements, e.g. riblets in a non-linear regime).

Fig. 14

Instantaneous iso-surfaces of the streamwise velocity fluctuations for the TS a and TD b configurations. The longitudinal plane presents contours of positive (solid) and negative (dashed) ($w^{\prime }$) that have been averaged along the streamwise direction. The streamlines drawn at the end lateral plane have been obtained by averaging the $u^{\prime }$ and $v^{\prime }$ along the spanwise direction

Finally, we have also extended the scaling arguments presented in the context of sparse and dense canopies to the transitional regime, where the mean drag offered by the filaments is comparable to the skin frictional drag of the canopy bed (Nepf 2012). In particular, the velocity fluctuations scaled with the local friction velocity computed as a sum of the viscous and Reynolds stresses present a good collapse of the velocity profiles. In the outer region, these profiles agree well with the results obtained for turbulent channel flow at a moderately high Reynolds number.