A Dual-Grid Hybrid RANS/LES Model for Under-Resolved Near-Wall Regions and its Application to Heated and Separating Flows

Abstract

A hybrid RANS/LES model for high Reynolds number wall-bounded flows is presented, in which individual Reynolds-Averaged Navier-Stokes (RANS) and Large Eddy Simulations (LES) are computed in parallel on two fully overlapping grids. The instantaneous, fluctuating subgrid-scale stresses are blended with a statistical eddy viscosity model in regions where the LES grid is too coarse. In the present case, the hybrid model acts as a near-wall correction to the LES, while it retains the fluctuating nature of the flow field. The dual computation enables the LES to be run on isotropic grids with very low wall-normal and wall-parallel resolution, while the auxiliary RANS simulation is conducted on a wall-refined high-aspect ratio grid. Running distinct, progressively corrected simulations allows a clearer separation of the mean and instantaneous flow fields, compliant with the fundamentally dissimilar nature of RANS and LES. Even with the wall-nearest grid point lying far in the logarithmic layer, velocity and temperature predictions of a heated plane channel flow are corrected. For a periodic hill flow, the dual-grid system improves the boundary layer separation and velocity field prediction both for a constant-spaced and a wall-refined LES grid.

1 Introduction

With the available computational resources of today, turbulence-resolving LES is becoming more attractive for application in industrial purposes. In contrast to statistical RANS schemes, LES enables the prediction of the instantaneous flow field, including pressure and temperature fluctuations, which are determinants of fatigue of critical components in thermal-hydraulics systems. The conduct of LES is however constrained by its high computational cost, which is related to the grid point number N_xyz needed to sufficiently resolve the turbulence scale range. For a wall-bounded flow, it is estimated to be exponentially correlated to the flow Reynolds number as N_xyz ∝ Re^13/7 [1], with the majority of the grid points located in the near-wall region in order to resolve anisotropic turbulence therein. In specific, it is the wall-nearest 10% of the boundary layer, where the required grid point number scales with the Reynolds number with high exponent. Piomelli [2] estimates that at moderate Reynolds numbers (Re ≈ 10⁴), around half of the total grid points have to lie in the inner part of the boundary layer.

To overcome the grid point problem for high Reynolds number flows, the effects of near-wall turbulence can be modelled, what is known as “wall-modelled LES” (WMLES). This set of models includes numerous wall function formulations, which set the wall shear stress in relation to the velocity in the near-wall region. However, justification of wall functions is low for non-equilibrium boundary layers, where the flow does not adhere to the law of the wall. WMLES based on velocity-profile-to-shear-stress correlations cannot be used to predict the wall heat transfer where the Reynolds friction-factor/Nusselt analogy breaks down, e.g. under a wall-impinging jet or at the reattachment point of a flow separation bubble.

Hybrid RANS/LES schemes [3] have been introduced as an alternative to wall functions, where the simulation locally switches from a turbulence-resolving mode to a statistical mode, taking advantage of the weak Reynolds number correlation of the RANS grid resolution requirements. In the context of hybrid RANS/LES, the term “RANS” generally refers to an “unsteady RANS” (URANS) scheme. One of the major hybrid schemes is the Detached Eddy Simulation (DES) family [4]. With multiple development stages, the more recent Improved Delayed DES (IDDES) model [5] is capable of predicting semi-confined flows with high accuracy on grids with low wall-parallel grid resolution, as demonstrated for example for periodic hill and backward-facing step flows [6, 7].

A number of hybrid models are based on turbulence resolution as in LES with additional near-wall RANS correction, e.g. [8, 9], and follow a blending approach to enable a gradual transition between RANS and LES mode. A subgrid-scale (SGS) turbulence variable of the LES scheme Φ^LES is blended with a RANS turbulence model quantity Φ^RANS to form the hybrid SGS model Φ^SGS, which is controlled with a transition function $\mathcal {F}$ as

$$ {\varPhi}^{\text{SGS}}=\mathcal{F}{\varPhi}^{\text{LES}}+\left( 1-\mathcal{F}\right){\varPhi}^{\text{RANS}}. $$

(1)

The function $\mathcal {F}$ is contained between zero and unity. In practice, Φ is a turbulence variable, e.g. the Reynolds stress tensor, turbulent kinetic energy, or eddy viscosity. The prediction quality of the hybrid model is highly dependent on the local transition from RANS to LES mode, and vice versa. Early methods without blending functions, but sharp transitions [10], exhibit a “log-layer mismatch” phenomenon, where a sudden increase of the mean velocity gradient occurs, before returning to the classic “dU⁺/dy⁺ = 1/κy⁺” log-law further above (with κ being the von Kármán constant). This is caused by a “resolved shear-stress depletion” near the sharp interface, quite understandably as resolved eddies, straddling or moving up and down across it, are weakened by the sudden increase in turbulent viscosity in the RANS layer. Visible effects are an under-predicted skin friction coefficient and a layer of non-physical, elongated eddy structures situated above the RANS layer, so-called “super-streaks” [11, 12]. Corrective approaches include for example a gradual transitional layer between RANS and LES sub-domains [13], forcing [14] or stochastic backscatter [15] to break up the super-streaks.

In fact, a cause for these lies in the non-compatibility of averaged and instantaneous variables, which may lead to an excessive damping of turbulent motions in vicinity of the RANS/LES interface. Uribe et al. [16] proposed a hybrid scheme, in which the mean SGS stresses are blended with Reynolds stresses predicted with a RANS model. With the term “Two Velocity Fields” model, they emphasise the different characteristics of instantaneous, fluctuating flow field, and its time-average. Coupling of the LES and RANS model is only undertaken on the mean field level, and the model clearly distinguishes between both flow fields. Results show that turbulence is maintained throughout the near-wall region and is able to transition across the seamless interface.

The differentiating perspective on the fluctuating and averaged flow fields is also found in non-blending approaches: Benarafa et al. [17] use an explicit forcing term in the momentum equation based on the deviation of the statistical RANS velocity from a moving averaged LES velocity field, while Xiao and Jenny [18] extend this concept also to transport equations for the turbulent kinetic energy and eddy dissipation rate. The RANS simulation is considered as the “driving” simulation near walls, while the opposite is true in the main flow region. Similarly, near-wall correction models for the LES Reynolds stresses with modelled RANS Reynolds stresses have been proposed, for example based on forcing terms [19] or changing the constant C_S of the dynamic Smagorinsky model [20]. The success of these models, without the use of artificial turbulence at the interface, but by simply treating mean and fluctuating velocity fields separately, strongly stands out.

Passive scalar transport has previously been demonstrated for various hybrid models in different applications, including pin matrix [21], ribbed channel [22] and impinging jet flows [23]. Rolfo, Uribe and Billard [24] presented an extension of the blending concept to the SGS turbulent heat flux as an alternative to the Simple Gradient Diffusion Hypothesis and demonstrated superior prediction of the Two Velocity Fields model to conventional LES for passive scalar transport on coarse grids.

Encouraged by the success of the Two Velocity Fields model, featuring the simple decomposition of SGS stresses, the seamless blending with the RANS eddy viscosity, and the hybrid scalar flux model for heat transfer, we here continue the development of this model. Apart from “Two Layer Models” (TLM) [25], where a supplemental, underlying RANS grid is used to bridge the gap between first LES grid point and the wall, wall-normal grid point reduction in combination with hybrid models is rarely found. A recent and substantially different approach to coarse-grid LES is the “Dual Mesh” model [18, 26], in which LES and RANS simulations are carried out in parallel on two independent grids, each optimised for their respective simulation scheme. A major difference between Xiao and Jenny’s work and TLM is the fully overlapping LES and RANS grid, which makes an a priori sub-domain specification obsolete, and avoids mismatched secondary log-layers at the interface. The present model follows their Dual Mesh approach, but combines it with the Reynolds stress blending method, where the degree of turbulence resolution by the computational grid governs the RANS contribution to the LES. On the other hand, a velocity blending approach feeds back from the LES to the RANS simulation wherever the grid is sufficiently refined. This stands in contrast to Xiao and Jenny’s model, where the LES is by default affected by the RANS at the wall-nearest 20% of the domain.

The remainder of this paper is organised as follows: The present hybrid model is described in Section 2, with the numerical setup given in Section 3. Results for a heated channel flow and periodic hill flow are compared with coarse LES and reference data in Section 4. Conclusions are drawn in Section 5.

2 Model Description

In LES, the governing equations of an incompressible flow with temperature as a passive scalar, including continuity, momentum transport and energy transport equations, are solved for filtered variables $\overline {\varPhi }$, i.e. HCode $\varPhi =\overline {\varPhi }+\phi ^{\prime \prime }$, with $\overline {(\cdot )}$ and $(\cdot )^{\prime \prime }$ denoting filtered and residual variables, respectively. The equations are written as

$$ \frac{\partial \overline{U}_{i}}{\partial x_{i}}=0, $$

(2)

$$ \frac{\partial \overline{U}_{i}}{\partial t}+\overline{U}_{j}\frac{\partial \overline{U}_{i}}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}+\frac{\partial}{\partial x_{j}}\left[\nu\left( \frac{\partial \overline{U}_{i}}{\partial x_{j}}+\frac{\partial \overline{U}_{j}}{\partial x_{i}}\right)-\tau_{ij} \right], $$

(3)

and

$$ \frac{\partial \overline{\varTheta}}{\partial t}+\overline{U}_{j}\frac{\partial \overline{\varTheta}}{\partial x_{j}}=\frac{\partial}{\partial x_{j}}\left( {\varGamma}\frac{\partial \overline{\varTheta}}{\partial x_{j}}-h_{j^{\prime\prime}}\right), $$

(4)

respectively. $\overline {U}_{i}$, $\overline {P}$, and $\overline {\varTheta }$ are the filtered velocity, pressure and passive scalar, and ρ, ν, Γ are the density, kinematic viscosity and molecular diffusivity, respectively. τ_ij is the residual stress tensor

$$ \begin{array}{@{}rcl@{}} \tau_{ij}=\overline{U_{i}U_{j}}-\overline{U}_{i} \overline{U}_{j} \end{array} $$

(5)

and $h_j^{\prime \prime }$ is the residual turbulent heat flux

$$ h_{j}^{\prime\prime}=\overline{U_{j}\varTheta}-\overline{U}_{j} \overline{\varTheta}, $$

(6)

which are modelled with the hybrid SGS formulation. The resolved Reynolds stress tensor and resolved turbulent heat flux are

$$ \begin{array}{@{}rcl@{}} R_{ij}^{\text{res}}=\langle\left( \overline{U}_{i}-\langle\overline{U}_{i}\rangle\right)\left( \overline{U}_{j}-\langle\overline{U}_{j}\rangle\right)\rangle \end{array} $$

(7)

and

$$ \begin{array}{@{}rcl@{}} H_{j}^{\text{res}}=\langle\left( \overline{U}_{j}-\langle\overline{U}_{j}\rangle\right)\left( \overline{\varTheta}-\langle\overline{\varTheta}\rangle\right)\rangle, \end{array} $$

(8)

respectively. $\langle {\Phi }\rangle ={\Phi }-\phi ^{\prime }$ denotes averaged variables, with $\phi ^{\prime }$ being the fluctuating part.

2.1 Blended SGS stress model

The blended SGS stress model stems from a formulation by Schumann [27], in which the deviatoric part of the model for τ_ij is decomposed into two contributing terms as

$$ \tau_{ij}-\frac{1}{3}\tau_{kk}\delta_{ij}=-2 {\nu_{t}^{r}}\left( \overline{S}_{ij}-\langle\overline{S}_{ij}\rangle\right)- 2{\nu_{t}^{a}}\langle \overline{S}_{ij}\rangle, $$

(9)

where

$$ \overline{S}_{ij}=\frac{1}{2}\left( \frac{\partial\overline{U}_{i}}{\partial x_{j}}+\frac{\partial\overline{U}_{j}}{\partial x_{i}}\right) $$

(10)

is the filtered strain-rate tensor, δ_ij is the Kronecker Delta, and ${\nu _{t}^{r}}$ and ${\nu _{t}^{a}}$ are modelled eddy viscosities. This decomposition assumes two contributions, which separately account for the isotropic fluctuating, and the inhomogeneous SGS stresses. Multiplying Eq. 9 with the instantaneous strain-rate tensor shows that the energy dissipation rate to the subgrid scale and contribution to the mean SGS stresses 〈τ_ij〉 are independently affected by ${\nu _{t}^{r}}$ and ${\nu _{t}^{a}}$, respectively. From this perspective, Schumann’s approach may be considered as the precursor to various present hybrid models. In the hybrid model framework of Uribe et al. [16], the blending concept (1) is introduced in Eq. 9 and the eddy viscosities are renamed to more explicitly identify the LES SGS eddy viscosity, and the RANS eddy viscosity, i.e.

$$ \tau_{ij}-\frac{1}{3}\tau_{kk}\delta_{ij}=-2f_{b}\nu_{t}^{\text{LES}}\left( \overline{S}_{ij}-\langle\overline{S}_{ij}\rangle\right)-2\left( 1-f_{b}\right) \nu_{t}^{\text{RANS}}\langle \overline{S}_{ij}\rangle. $$

(11)

f_b is a blending function described in Section 2.3, and $\nu _{t}^{\text {LES}}$ and $\nu _{t}^{\text {RANS}}$ are the eddy viscosities computed with the LES and RANS models described in Sections 2.4 and 2.5, respectively.

Methodical differences exist between the forcing approach by Xiao and Jenny [18, 19] and the present SGS stress blending method. In the original work [18], the instantaneous and mean velocity field are treated with dedicated corrective terms in the transport equations $Q_{i}^{\text {LES}}=f(U_{i}-\langle \overline {U}_{i}\rangle ,\langle R_{ij}\rangle ^{\text {LES}}-R_{ij}^{\text {RANS}})$. The mean velocity fields of LES and RANS simulations are forced to converge, while the fluctuations are scaled with the difference of the LES and RANS Reynolds stresses $\langle R_{ij}\rangle ^{\text {LES}}-R_{ij}^{\text {RANS}}$. In an alternative approach [19], the latter is taken as an explicit corrective term to match RANS and averaged LES velocity fields. Main advantage of the forcing approach is the preservation of fluctuation down to the wall.

In the present model, the LES is locally corrected by a RANS eddy viscosity model via the hybrid SGS stress formulation. The total LES stresses gradually transition from $R_{ij}^{\text {LES}}=R_{ij}^{\text {res}}-2\nu _{t}^{\text {LES}}(\overline {S}_{ij}-\langle \overline {S}_{ij}\rangle )$ for f_b = 1 to $R_{ij}^{\text {LES}}=-2\nu _{t}^{\text {RANS}}\langle \overline {S}_{ij}\rangle$ where f_b = 0, in other words where the grid is found to be too coarse to resolve any fluctuation. In practice, the latter case may occur very close to the wall or when the grid is massively coarsened.

2.2 Heat transfer

Rolfo, Uribe and Billard [24] transferred the blending method to a hybrid SGS turbulent heat flux with a two-part expression for a Simple Gradient Diffusion Hypothesis (SGDH) model as

$$ h_{j^{\prime\prime}}=-f_{b}{\varGamma}^{\text{LES}}\frac{\partial}{\partial x_{j}}\left( \overline{\varTheta}-\langle \overline{\varTheta}\rangle\right)-\left( 1-f_{b}\right){\varGamma}^{\text{RANS}}\frac{\partial}{\partial x_{j}}\langle\overline{\varTheta}\rangle, $$

(12)

with

$$ \begin{array}{@{}rcl@{}} {\varGamma}^{\text{LES}}=\frac{\nu_{t}^{\text{LES}}}{Pr_{t}^{\text{LES}}} \end{array} $$

(13)

and

$$ \begin{array}{@{}rcl@{}} {\varGamma}^{\text{RANS}}=\frac{\nu_{t}^{\text{RANS}}}{Pr_{t}^{\text{RANS}}} \end{array} $$

(14)

being scalar diffusivities of the LES and RANS contributions, respectively. $Pr_{t}^{\text {LES}}=0.75$ and $Pr_{t}^{\text {RANS}}=0.75$ are turbulent Prandtl numbers, which have been identified as optimal values on the one-grid framework.

2.3 Blending function

The blending function is a revised expression by Rolfo, Uribe and Billard [24], which includes the Smagorinsky constant C_S in the denominator to make the isotropic part of the modelled τ_ij less sensitive to the chosen value of C_S,

$$ f_{b}=\tanh\left[C_{l}\left( \frac{L_{t}}{C_{S}\varDelta}\right)^{n}\right]. $$

(15)

Here, f_b relates the characteristic length scale Δ = 2Ω^1/3, with Ω being the cell volume, to the turbulence length scale L_t = φk^3/2/ε. k, φ and ε are obtained from the BL-〈v²〉/k RANS eddy viscosity model [28], see Section 2.5. The inclusion of φ = 〈v²〉/k, being the ratio of wall-normal Reynolds stress component to the turbulent kinetic energy, dampens L_t as the wall is approached. C_l = 0.16 and n = 1 are model parameters, which return optimal values for the plane channel flow validation case. As outlined in Section 2.1, for f_b = 0, the modelled τ_ij is equivalent to the RANS Reynolds stresses. In contrast, with f_b = 1, only the fluctuating term on the r.h.s. of Eq. 11 remains. In addition to the near-wall transition, the blending function also enables a return to the RANS mode away from walls with f_b ≪ 1, if the LES grid is deliberately coarsened. The blending function acts analogously in the turbulent SGS heat flux h_j (12).

2.4 LES Eddy viscosity model

In contrast to the Smagorinsky SGS eddy viscosity model [29], which is based on the full instantaneous strain-rate tensor $\overline {S}_{ij}$, only the fluctuating part of the strain-rate tensor is considered here, as applied by Moin and Kim [30], with

$$ \nu_{t}^{\text{LES}}=\left( C_{S}{\varDelta}\right)^{2}\sqrt{2\left( \overline{S}_{ij}-\langle\overline{S}_{ij}\rangle\right)\left( \overline{S}_{ij}-\langle\overline{S}_{ij}\rangle\right)}. $$

(16)

For the Smagorinsky constant, the common value for channel flows of C_S = 0.065 is used. A van Driest damping term [31] is not employed in the hybrid model, since the blending function is found to be sufficient.

2.5 RANS Eddy viscosity model

The original Two Velocity Fields model uses an elliptic relaxation k-ε-φ-f model [32] to model the RANS eddy viscosity $\nu _{t}^{\text {RANS}}$, which is a robust version of the original 〈v²〉-f model by Durbin [33]. Consideration of the wall-normal Reynolds stress component 〈v²〉 more accurately accounts for the wall blocking effect without using damping functions. f is related to the redistribution of turbulent kinetic energy from the wall-normal to the wall-parallel components and is a solution of an elliptic equation. In the present work, $\nu _{t}^{\text {RANS}}$ is taken from the BL-〈v²〉/k model by Billard and Laurence [28], which employs the elliptic blending method [34] to further improve the model quality in respect to the Reynolds number and robustness by blending near-wall and homogeneous models of turbulent quantities. This turbulence model is a low-Reynolds model and thus does not require a wall function, but the first grid point layer off the wall to be at y⁺ ≈ 1. The following summarises the model used in the present study. All turbulence quantities of the BL-〈v²〉/k model, in particular the transport equations for k, ε and φ, are computed with the blended RANS velocity field 〈U_i〉, which is introduced in Section 2.7.

The turbulent kinetic energy is determined by the modified transport equation

$$ \begin{array}{@{}rcl@{}} \frac{\mathrm{D}k}{\mathrm{D}t}&= & \mathcal{P}_{k}-\varepsilon+\frac{\partial}{\partial x_{j}}\left[\left( \frac{\nu}{2}+\frac{\nu_{t}}{\sigma_{k}}\right)\frac{\partial k}{\partial x_{j}}\right]\\ &&-C_{\varepsilon3}\left( 1-\alpha\right)^{3}\frac{k}{\varepsilon}2\nu\nu_{t}\left( \frac{\partial}{\partial x_{k}}\frac{\partial}{\partial x_{j}}\langle U_{i}\rangle\right)\left( \frac{\partial}{\partial x_{k}}\frac{\partial}{\partial x_{j}}\langle U_{i}\rangle\right), \end{array} $$

(17)

where $\mathcal {P}_{k}$ is the production of turbulent kinetic energy. The appearance of the halved molecular viscosity and the third r.h.s. term originates from introducing the E-term

$$ E=2\nu\nu_{t}\left( \frac{\partial}{\partial x_{k}}\frac{\partial}{\partial x_{j}}\langle U_{i}\rangle\right)\left( \frac{\partial}{\partial x_{k}}\frac{\partial}{\partial x_{j}}\langle U_{i}\rangle\right) $$

(18)

as proposed by Jones and Launder [35]. It is implicitly inserted via the change of variable

$$ \varepsilon\rightarrow\varepsilon+\frac{k}{\varepsilon}E+\frac{1}{2}\nu\frac{\partial}{\partial x_{j}}\frac{\partial}{\partial x_{j}}k. $$

(19)

The transport equation for the dissipation rate ε reads as

$$ \frac{\mathrm{D}\varepsilon}{\mathrm{D}t}=\frac{C_{\varepsilon1}\mathcal{P}_{k}-C_{\varepsilon2}^{*}\varepsilon}{T}+\frac{\partial}{\partial x_{j}}\left[\left( \frac{\nu}{2}+\frac{\nu_{t}}{\sigma_{\varepsilon}}\right)\frac{\partial\varepsilon}{\partial x_{j}}\right], $$

(20)

where $C_{\varepsilon 2}^{*}$ is functional of the turbulent diffusion of k, $\partial /\partial x_{j}\left (\nu _{t}/\sigma _{k}\partial k/\partial x_{j}\right )$. $C_{\varepsilon 2}^{*}$ transitions from the conventional value of C_ε2 = 1.83 in the log-layer to a smaller value in the defect layer for an improved prediction of the velocity therein:

$$ C_{\varepsilon2}^{*}=C_{\varepsilon2}+\alpha^{3}\left( C_{\varepsilon4}-C_{\varepsilon2}\right)\tanh\left( \left|\frac{\frac{\partial}{\partial x_{j}}\left( \nu_{t}/\sigma_{k}\frac{\partial k}{\partial x_{j}}\right)}{\varepsilon}\right|^{3/2}\right). $$

(21)

φ is determined by the transport equation

$$ \frac{\mathrm{D}\varphi}{\mathrm{D}t}=\underset{f}{\underbrace{\left( 1-\alpha^{3}\right)f_{w}+\alpha^{3}f_{h}}}-\mathcal{P}_{k}\frac{\varphi}{k}+\frac{2}{k}\frac{\nu_{t}}{\sigma_{k}}\frac{\partial\varphi}{\partial x_{j}}\frac{\partial k}{\partial x_{j}}+\frac{\partial}{\partial x_{j}}\left[\left( \frac{\nu}{2}+\frac{\nu_{t}}{\sigma_{\varphi}}\right)\frac{\partial\varphi}{\partial x_{j}}\right]. $$

(22)

The scalar parameter f is constructed as a blend of the near-wall form

$$ f_{w}=-\frac{\varepsilon}{2}\frac{\varphi}{k} $$

(23)

and the homogeneous form

$$ f_{h}=-\frac{1}{T}\left( C_{1}-1+C_{2}\frac{\mathcal{P}_{k}}{\varepsilon}\right)\left( \varphi-\frac{2}{3}\right). $$

(24)

The blending itself is governed by the non-dimensional wall-proximity parameter α, for which an elliptic differential equation is solved,

$$ \alpha-L^{2}\frac{\partial}{\partial x_{j}}\left( \frac{\partial\alpha}{\partial x_{j}}\right)=1, $$

(25)

with the turbulence model’s own length scale

$$ L=\sqrt{{C_{L}^{2}}\left( \frac{k^{3}}{\varepsilon^{2}}+C_{\eta}^{2}\frac{\nu^{3/2}}{\varepsilon^{1/2}}\right)}, $$

(26)

featuring the integral and the Kolmogorov length scale. The boundary condition is α|_w = 0 and α approaches unity with increasing wall distance. α is a feasible wall proximity parameter also for complex geometries, where the definition of the wall-distance may be non-trivial. Note that the third power exponent for α is introduced differently in Eqs. 17 and 22 by Billard and Laurence [28]. The resulting eddy viscosity is

$$ \nu_{t}^{\text{RANS}}=C_{\mu}\varphi k \min\left( T,T_{\lim}\right), $$

(27)

with the turbulence time scale

$$ T=\sqrt{\frac{k^{2}}{\varepsilon^{2}}+{C_{T}^{2}}\frac{\nu}{\varepsilon}} $$

(28)

and limiter

$$ T_{\lim}=\frac{0.6}{\sqrt{6}C_{\mu}\varphi\sqrt{\langle S_{ij}\rangle\langle S_{ij}\rangle}} $$

(29)

to correct for an excessive production rate. See Table 1 for values of all model constants and [28] for a complete model description.

Table 1 Model constants of the elliptic blending BL-〈v²〉/k model

2.6 Time-averaging

The averaging operation for the filtered variable $\overline {\varPhi }$ is performed with very little computational effort as a running time-average at each numerical time step n,

$$ \langle \overline{\varPhi}\rangle^{\mathrm{n+1}} =\gamma\overline{\varPhi}^{\mathrm{n}+1}+\left( 1-\gamma\right) \langle\overline{\varPhi}\rangle^{\mathrm{n}}, $$

(30)

with γ as an averaging parameter γ is generally chosen as such that the averaging period is substantially longer than the eddy turnover time scale. However, while a too large averaging period increases convergence time, a too short period leads to excessive fluctuations. As in the baseline Two Velocity Fields model, γ = 10Δt ⋅ u_τ/δ is used for the plane channel flow, with Δt being the physical time step, $u_{\tau }=\sqrt {\tau _{w}/\rho }$ being the friction velocity, τ_w being the wall shear stress and δ being the channel half width [24]. As referencing to the nominal u_τ is only found feasible for the plane channel flow case with a prescribed friction Reynolds number Re_τ = u_τδ/ν, γ = 0.05Δt ⋅ U_b/h with U_b being the bulk velocity at the hill crest and h as the hill height is used for the periodic hill test case.

2.7 Dual-grid simulation

In the present work, the Two Velocity Fields model is extended for the use on grids with low wall-normal resolution. Without relying on a wall function for the RANS turbulence model, the grid has to be sufficiently resolved in wall-normal direction, i.e. to meet the criterion of the wall-normal distance of the wall-nearest cell centre being $y^{+}_{1}=y_{1}u_{\tau }/\nu \leq 1$ in order to capture a correct velocity-wall shear stress relationship.

The concept of Xiao and Jenny [18] of computing RANS and LES on separate, but fully overlapping RANS and LES grid, is here adopted to approach this constraint. This allows a use of optimised topologies for each modelling strategy, i.e. a quasi-isotropic LES grid, and a high-aspect-ratio wall-refined RANS grid. In contrast to their model, where explicit source terms in the momentum and turbulence transport equations are employed to couple the LES and RANS simulation, the present approach is based on a two-way coupling between both simulations: First, the RANS simulation introduces the RANS eddy viscosity $\nu _{t}^{\text {RANS}}$ to the LES where the grid is too coarse (11). Second, the LES returns its time-averaged velocity field $\langle \overline {U}_{i}\rangle$ to the RANS simulation. This is realised with a continuous blending of both velocity fields in the auxiliary RANS simulation, which can be written as

$$ \langle U_{i}\rangle^{\mathrm{n+1}}=f_{\alpha}\langle\overline{U}_{i}\rangle^{\mathrm{n}}+\left( 1-f_{\alpha}\right)\langle U_{i}\rangle^{\mathrm{n}}. $$

(31)

f_α = α² is a blending function based on the wall proximity parameter α and is obtained from the elliptic equation (25). The velocity blending in Eq. 31 can be interpreted as follows: Prior to the resolution of the RANS turbulence variables for the time step n + 1 in the auxiliary RANS simulation, the time-averaged velocity field $\langle \overline {U}_{i}\rangle$ received from the primary LES simulation is updated with a blend of the RANS velocity 〈U_i〉 and $\langle \overline {U}_{i}\rangle$ from time step n, according to the local value of the blending function f_α. As such, the velocity field is equivalent to the RANS velocity 〈U_i〉 for f_α = 0 at walls, while away from walls with f_α = 1, the velocity shall converge to the LES time-averaged velocity. In turn, this expression enables the RANS turbulence model equations to be solved on the RANS velocity field near walls, rather than on the LES time-averaged field, where a grid-to-grid interpolation from the coarse LES field to the wall-refined RANS grid method is not suitable for an accurate gradient reconstruction. Since this issue is only considered in the near-wall region, α as a wall-distance parameter is chosen, rather than the flow-dependent length scale comparison L_t/(C_SΔ) as in f_b (15). It is emphasised that the velocity blending method only implicitly affects the primary LES via the resulting $\nu _{t}^{\text {RANS}}$ in Eq. 11, with the blended velocity field having no explicit influence on the LES.

3 Numerical Setup

The open-source finite volume solver Code_Saturne [37] is used to implement the proposed hybrid model. This solver is extensively used on high performance computing systems with highly parallelised processes. The code is chosen as it offers a variety of state-of-the-art turbulence models, and as it can handle meshes with any type of cell and topology. To account for the computation of RANS and LES on two grids, simulations are run in parallel and are coupled via Message Passing Interface (MPI) available in the software, which allows the solver to couple with one or more fluid or solid solvers, including other instances of Code_Saturne. L_t and $\nu _{t}^{\text {RANS}}$ are transferred to the LES, while the averaged LES velocity field $\langle \overline {U}_{i}\rangle$ is returned to the RANS simulation at each numerical time step. The data is interpolated onto the respective grids before the discretised equations are solved. The velocity-pressure algorithm is solved with a segregated prediction/correction scheme, similar to the SIMPLEC scheme [38]. The Rhie and Chow interpolation is used to avoid oscillations. For the solution of the velocity, turbulence transport and passive scalar, a Jacobi system is solved, while a multigrid algorithm is applied for the pressure Poisson equation. The time step Δt is constant and identical for RANS and LES, and is chosen as such that the maximum Courant number is below unity for all simulations. The transport equations of turbulence variables are discretised in time with a second order Crank-Nicolson scheme for the LES, and first order for the RANS simulation. The physical properties are extrapolated with the second-order Adams-Bashforth scheme.

4 Results

4.1 Heated plane channel flow

The fully developed turbulent plane channel flow is computed at friction Reynolds numbers Re_τ = u_τδ/ν ∈{395;1,020;2,022;4,079;10,000}. The domain has a size of L_x × L_y × L_z = 6.4δ × 2δ × 3.2δ and is periodic in streamwise (x) and spanwise (z) directions, with walls in the remaining (y) direction. The flow is maintained with a constant pressure gradient in x-direction to obtain the prescribed friction Reynolds number.

The fluid (Pr = 0.71) is heated with a volume source term to balance the desired uniform scalar flux q_w across the walls. The numerical boundary condition for the temperature field is Θ|_w = 0. Velocity and temperature fields for flows up to Re_τ = 4,079 are compared with DNS data [39,40,41], while the mean velocity and temperature profiles at Re_τ = 10,000 are benchmarked against the logarithmic parts of the law of the wall, i.e.

$$ \begin{array}{@{}rcl@{}} U^{+}=\frac{1}{\kappa}\ln y^{+}+5.2, \end{array} $$

(32)

with κ = 0.41 and

$$ \begin{array}{@{}rcl@{}} {\varTheta}^{+}=\frac{1}{\kappa_{\varTheta}}\ln y^{+}+3.0 \end{array} $$

(33)

for the temperature field, with κ_Θ = 0.43. The hybrid model is demonstrated on two grid types: First, on wall-refined grids with $y^{+}_{1}=1$ for all Re_τ numbers and large grid spacings in wall-parallel directions, as they are usually employed for hybrid RANS/LES models. The grids have N_x × N_y × N_z = 40 × 40 × 32 grid points, and 80 × 80 × 64 grid points for the simulations at Re_τ = 10,000. Second, on an isotropic grid with 128 × 41 × 64 grid points, which is identical for all Reynolds numbers, and high values $y^{+}_{1}$ for the wall-nearest grid point. The LES grid characteristics are given in Table 2, including the constant grid spacing Δx⁺ and Δz⁺ in wall-parallel directions, ${\varDelta } y^{+}_{\delta }$ as the wall-normal grid spacing closest to the channel centre line y = δ, and the non-dimensional numerical time step Δt ⋅ u_τ/δ. The auxiliary RANS simulations are all carried out on wall-refined high-aspect ratio grids (N_y = 128, $y^{+}_{1}\leq 1$ for all Reynolds numbers) for the same domain. It is stressed here that the grid spacing at the higher Reynolds numbers is too coarse to be considered as an adequate LES by itself, as it does not meet the conventions on LES grid resolution for wall-bounded flows, i.e. Δx⁺ ≈ 100, Δz⁺ ≈ 20, and $y^{+}_{1}\leq 1$ [42]. It is therefore referred to as “coarse LES”, to which additional comparisons are made to emphasise the impact of the hybrid model in respect to the prediction quality and the computational overhead due to coupling with the RANS simulation. An instantaneous wall function with the relation $\overline {U}_{i}/u_{\tau }=y^{+}$ for y⁺ < 10.88 and $\overline {U}_{i}/u_{\tau }=1/\kappa \ln y^{+}+5.2$ for y⁺ ≥ 10.88 is used for the standalone LES.

Table 2 Simulation and LES grid characteristics for the plane channel flow at all Re_τ numbers

4.1.1 Wall-refined grid

The hybrid model is first demonstrated on the wall-refined grid at Re_τ = 395 (Fig. 1). The mean streamwise velocity component $U^{+}=\langle \overline {U} \rangle /u_{\tau }$ (Fig. 1a) follows the reference from the viscous sublayer to the outer region well and much better than the coarse LES. A comparable improvement is obtained for the prediction of the temperature ${\varTheta }^{+}=\left (\langle \overline {\varTheta }\rangle -\varTheta |_{w}\right )/\theta _{\tau }$, with $\theta _{\tau }=q_{w}/\left (\rho c_{p} u_{\tau } \right )$ being the friction temperature (Fig. 1b). However, the buffer layer is flatter and the slope of the predicted log-layer is higher than of the reference. This is in contrast to well-agreeing profiles at Pr = 1 reported by Rolfo, Uribe and Billard [24]. Extensive testing on the blending function f_b for the passive scalar transport has shown that the present model is more sensitive to the choice of $Pr_{t}^{\text {RANS}}$ and the related mean contribution to h_j than the one-simulation model. The mean Reynolds shear stress component $R_{12}^{+}=\langle R_{12}\rangle /u_{\tau }^{2}$, decomposed into the resolved, SGS, and total (R₁₂) values, is given in Fig. 1c. The hybrid model corrects the SGS contribution in the viscous sublayer, resulting in a fully overlapping total Reynolds shear stress with the DNS. In case of the coarse LES, the SGS model is unable to return the correct magnitude, which is related to the over-predicted velocity profile. The mean turbulence intensities, given as root mean squares (rms) $\left (u^{\prime }_{i}\right )^{+}_{\text {rms}}=\sqrt {\langle u_{i}^{\prime 2}\rangle }/u_{\tau }$ (Fig. 1d), are overall closer to the benchmark than the standalone coarse LES. In particular, the near-wall peak of $u^{\prime }_{\text {rms}}$ is corrected by the hybrid SGS model. The decomposed turbulent heat flux component $H_{2}^{+}=H_{2}/(u_{\tau }\theta _{\tau })$ (Fig. 1e) shows an equivalent correction up to y⁺ ≈ 40 as the Reynolds shear stress, where the modelled $h_{2}^{\prime \prime }$ delivers an increased contribution to the total H₂. The temperature variance $\theta ^{\prime +}_{\text {rms}}=\sqrt {\langle \theta ^{\prime 2}\rangle }/\theta _{\tau }$ (Fig. 1f) is reduced near the wall and is now closer to the reference than the coarse LES. Overall, the dual-grid system is showing a comparable improvement as the original one-simulation model [16] on the identical grid (results not included here).

Fig. 1

Mean profiles for the plane channel flow at Re_τ = 395 on the wall-refined grid: a streamwise velocity U⁺; b temperature Θ⁺; c Reynolds shear stress $R_{12}^{+}$; d turbulence intensities $\left (u^{\prime }_{i}\right )^{+}_{\text {rms}}$; e turbulent heat flux $H_{2}^{+}$; f temperature variance ${\theta ^{\prime }}^{+}_{\text {rms}}$

4.1.2 Isotropic grid

The model testing is then extended to the isotropic grid topology, for which the present hybrid model is designed. The profile of the mean streamwise velocity U⁺ at Re_τ = 395 (Fig. 2a) shows a very good agreement with the reference, where the profiles follow the log-law with a correct slope. Also included here is the mean velocity of the underlying RANS simulation on the wall-refined auxiliary grid, which predicts the flow field well in the inner and buffer layers. The coarse LES (with a wall function) returns a steeper slope in the buffer layer and an overall over-prediction of U⁺.

Fig. 2

Mean profiles for the plane channel flow at Re_τ = 395 on the isotropic grid: a streamwise velocity U⁺; b temperature Θ⁺; c Reynolds shear stress $R_{12}^{+}$; d turbulence intensities $\left (u^{\prime }_{i}\right )^{+}_{\text {rms}}$; e turbulent heat flux $H_{2}^{+}$; f temperature variance ${\theta ^{\prime }}^{+}_{\text {rms}}$

The prediction for the mean temperature profile Θ⁺ (Fig. 2b) by the hybrid model is qualitatively lower than for the velocity, with a log-layer slope parallel to the coarse LES and a little dip above the buffer layer. The auxiliary RANS temperature field is not overlapping with the (hybrid) LES simulation, indicating that the velocity coupling is not analogously transferred to the passive scalar field. The mean decomposed Reynolds shear stress component $R_{12}^{+}$ is shown in Fig. 2c. In case of the hybrid model, the total stresses R₁₂ overlap with the reference above y⁺ ≈ 40. On this grid topology, a sharp peak is observed for both hybrid RANS/LES and the coarse LES, where the low wall-normal grid resolution adversely affects the velocity gradient reconstruction. The hybrid SGS model however redistributes the near-wall peak of the SGS shear stress τ₁₂, correcting the observed shear stress at the first grid point in comparison to the coarse LES. This has been analogously observed for the flows at higher Reynolds numbers. The turbulence intensities $\left (u^{\prime }_{i}\right )^{+}_{\text {rms}}$ (Fig. 2d) are generally well-predicted for all components on the isotropic grid. While both simulations mostly overlap, the intensities are slightly lower near the wall for the hybrid model. This is an indication of minimal turbulence damping effects due to the RANS contribution.

The turbulent heat flux component $H_{2}^{+}$ (Fig. 2e) overall agrees with the reference. The near-wall peak seen for the Reynolds shear stress is less excessive. In comparison with the coarse LES, the SGS model contribution near the wall is increased. The temperature variance $\theta ^{\prime +}_{\text {rms}}$ (Fig. 2f) is only slightly lower than the reference away from the wall, yet, the wall-normal resolution is too coarse to return the near-wall peak . Similar to $\left (u^{\prime }_{i}\right )^{+}_{\text {rms}}$, the comparison to the coarse LES shows small damping effect of the fluctuation due to the RANS contribution.

4.1.3 Higher Reynolds numbers

The mean velocity and temperature profiles for all considered Reynolds numbers and grid types are summarised in Figs. 3 and 4. For the higher Reynolds number cases, the model leads to a similar improvement of the velocity log-layer prediction. However, larger systematic discrepancies between the hybrid model and the reference are seen for the mean temperature profiles in the channel core, while the near-wall RANS sub-domain remains correct.

Fig. 3

Mean velocity profiles U⁺ for the plane channel flow for all Reynolds numbers: a wall-refined grid; b isotropic grid. Vertical offset of five units between different Reynolds numbers for clarity

Fig. 4

Mean temperature profiles Θ⁺ for the plane channel flow for all Reynolds numbers: a wall-refined grid; b isotropic grid. Vertical offset of five units between different Reynolds numbers for clarity

The mean profiles of the blending function f_b for both grid topologies (Fig. 5) and the wall proximity function f_α (Fig. 6) over the relative wall distance y/δ give an impression of the local blend of the RANS contribution into the hybrid SGS model and the mean velocity fields, respectively. Note that f_α is only computed and needed in the auxiliary RANS simulation. The fine resolution on the wall-refined grids (Figs. 5a) enables f_b to converge to zero at the first grid points. The transition of f_b is flow- and grid-dependent and remains fairly unchanged in wall distance, partially because the wall-normal grid refinement has been optimised for each flow Reynolds number (to obtain $y^{+}_{1}=1$). On the isotropic grid, however, the near-wall gradients of f_b are not resolved, as the grid resolution is too low (Fig. 5b). An increasingly earlier transition $f_{b}\rightarrow 1$ for increasing Re_τ is visible as the grid remains unchanged for the higher Reynolds number cases. In contrast to f_b, the profile of f_α and hence the mean velocity field blending depends solely on the flow condition.

Fig. 5

Mean profiles of the blending function f_b for the plane channel flow for all Reynolds numbers: a wall-refined grid; b isotropic grid

Fig. 6

Mean profiles of the wall proximity function f_α for the plane channel flow for all Reynolds numbers on the auxiliary grid (see Fig.5 for legend)

Figure 7 compares the skin friction coefficient $C_{f}=\tau _{w} /\left (0.5\rho {U_{b}^{2}}\right )$, with U_b being the bulk velocity, to the DNS and the estimation $C_{f}=0.073Re_{b}^{-0.25}$ by Dean [43]. On the wall-refined grid, the coarse LES is inconsistently over- or under-predicting, while on the isotropic grid it is continuously under-predicting the skin friction in conjunction with an excessive bulk Reynolds number. The hybrid model is closer to the references than the coarse LES, both with the skin friction and the predicted bulk Reynolds number Re_b = 2U_bδ/ν. It is observed that, with an increasing friction Reynolds number, the LES deviates in predicted bulk Reynolds number and C_f value from both DNS and estimated values, while the hybrid model is closer to DNS reference results in both Re_b and C_f. Relative errors in C_f to the DNS (and the formula by Dean for Re_τ = 10,000) are summarised in Table 3, which are found to be in reasonable limits for both types of grids with the highest deviation of 13.4% at Re_τ = 2,022. The latter is possibly related to the RANS/LES switch in the buffer layer on the chosen grid. An additional “mid-buffer layer switch prevention” criterion in the expression for f_b might therefore be useful.

Fig. 7

Skin friction coefficient C_f over predicted bulk Reynolds number Re_b for the hybrid model and coarse LES on isotropic and wall-refined grids

Table 3 Relative skin friction coefficient error for the different cases

4.1.4 Instantaneous flow field

An analysis of the instantaneous flow field gives an insight into the reproduction of turbulent motions on the coarse LES grid, in particular in the vicinity of the RANS-driven layers. Coherent structures are visualised with iso-surfaces of the Q-criterion, which is the second invariant of the velocity gradient tensor (Fig. 8). The iso-surfaces are coloured with the instantaneous streamwise velocity. The formation of large turbulent structures near the walls is recognisable, although the grid resolution is much lower than of a wall-resolving LES. Yet, visualisation of small structures such as hairpin vortices is not possible on these grids.

Fig. 8

Iso-surface of Q for the hybrid model at Re_τ = 395, coloured with instantaneous streamwise velocity U⁺ on the isotropic grid

Additional plotting of the instantaneous velocity vectors at Re_τ = 395, projected in (y, z)-plane (Fig. 9), displays continuous sweeps and ejections in the RANS-driven near-wall regions, marked by iso-lines of the mean blending function f_b. This feature is directly related to the avoidance excessive damping at the RANS/LES interface, which otherwise would lead to a log-layer mismatch as discussed in the introduction.

Fig. 9

Instantaneous velocity vectors and iso-lines of f_b in (y, z)-plane at Re_τ = 395: a wall-refined grid; b isotropic grid

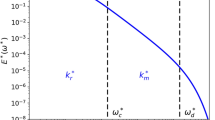
The effect of the hybrid SGS model is furthermore investigated by means of one-dimensional energy spectra $E_{uu}^{+}\left (\kappa _{x}\right )$ of the streamwise velocity fluctuation at Re_τ = 10,000 on the isotropic grid (Fig. 10). κ_x is the wavenumber in streamwise direction. The energy spectra are shown at two locations, y⁺ = 244, which corresponds to the first grid point off the wall, and y/δ = 1 at the centre line. The switch to a full LES mode occurs approximately at the fourth grid point (y⁺ ≈ 1,000, see Fig. 5b). Near the wall, the hybrid model exhibits slightly higher values at a larger wavenumber range than the baseline coarse LES. Yet, at y/δ = 1, where the RANS model is not used, nearly the identical distributions are seen.

Fig. 10

Energy spectra of the streamwise velocity fluctuation for the plane channel flow at Re_τ = 10,000 on the isotropic grid: a near the wall (y⁺ = 244); b at the centre line (y/δ = 1)

4.2 Periodic hill flow

The hybrid model is assessed on a channel flow constricted by periodic hills (geometry defined by Almeida et al. [44]) along the bottom wall at a bulk Reynolds number of Re_b = 10,595, based on the hill height h and bulk velocity U_b at the hill crest. The dimensions of the domain are L_x = 9h, L_y = 3.036h and L_z = 4.5h in streamwise, wall-normal and spanwise direction, respectively. The flow is driven by a mass source term to maintain the desired bulk Reynolds number. The periodic hill flow has been well investigated by others at various Reynolds numbers by means of experiments, DNS and LES. Primary challenge of this flow regime for numerical simulations is the correct prediction of the pressure-induced flow separation on the downstream side of the hill and the resulting shape and length of the recirculation bubble.

Two computational grids are employed for the LES part of the dual-grid simulations, which enable a comparison with results of the Dual Mesh approach by Xiao and Jenny [18] and of the IDDES by Mockett et al. [7]. First, standalone LES and hybrid simulations are run on a wall-refined grid with N_x × N_y × N_z = 100 × 80 × 80 and maximum wall distance of the first grid points of $y^{+}_{1}\leq 1$ on all walls (Fig. 11a). In a second case, a fully constant-spaced grid with only N_x × N_y × N_z = 100 × 50 × 40 and $y^{+}_{1}\leq 27$ (Fig. 11b) is used. The cell distribution is similar to the grid employed by Xiao and Jenny [18] (N_xyz ≈ 0.1 ⋅ 10⁶) and the constant-spaced grid by Mockett et al. [7] (N_xyz ≈ 1.5 ⋅ 10⁶).

Fig. 11

Computational grids for the periodic hill flow (every second grid point shown): a wall-refined grid; b constant-spaced grid

The auxiliary RANS simulation in the dual-grid system is carried out on a wall-refined grid with the same topology in (x, y)-plane as the wall-refined LES grid, while the periodicity in spanwise direction is exploited to reduce the number of grid points. Grid and simulation characteristics are summarised in Table 4, including the normalised boundary layer separation and reattachment locations x/h and non-dimensional numerical time step Δt ⋅ U_b/h.

Table 4 Simulation characteristics for the periodic hill flow

The mean streamlines and contours of the normalised streamwise velocity component 〈U〉/U_b, as depicted in Fig. 12, give an impression of the overall flow condition. The hybrid model returns a similar recirculation bubble in terms of shape and length as of the benchmark for both grid qualities. On the constant-spaced grid, little differences are observed downstream of the boundary layer separation point. Results for the conventional LES (with wall function) on the constant-spaced grid are included to show the corrective effect of the hybrid SGS model. It is again emphasised that this grid is too coarse near the walls to conduct an ordinary LES, especially in x direction to expect high accuracy in capturing the recirculation. As a result, the velocity near the hill crest is over-predicted and the recirculation bubble is overly short and flat.

Fig. 12

Mean streamlines of the periodic hill flow: a reference (from [45]); b hybrid (wall-refined grid); c hybrid (constant-spaced grid); d coarse LES (constant-spaced grid)

Profiles of 〈U〉/U_b, cross-stream velocity 〈V 〉/U_b, as well as the total shear stress component R₁₂ at ten equidistant stations in streamwise direction x/h are shown in Fig. 13. The mean velocity for the hybrid model on both grids is closer to the reference, especially 〈U〉 at the critical region around the hill crest (x/h = 0) is corrected on the constant-spaced grid. The SGS shear stress component shows largest improvements in the recirculation area at x/h = 1 and x/h = 2.

Fig. 13

Mean profiles of the periodic hill flow: a streamwise velocity 〈U〉/U_b; b cross-stream velocity 〈V 〉/U_b; c total shear stress component $\langle R_{12}\rangle /{U_{b}^{2}}$

The profile of the mean skin friction coefficient C_f predicted by the hybrid model is compared to the benchmark and two reported IDDES results on a similar wall-refined and a y-constant-spaced grid [7] see Fig. 14. The hybrid simulation on the wall-refined grid agrees very well with the benchmark and performs similarly to the wall-refined IDDES. In contrast, the dual-grid model returns a very different profile on the constant-spaced grid, where the near-hill peaks are under-predicted upwind and over-predicted downwind of the hill. In comparison to the IDDES on the constant-spaced grid, the results are slightly better, however, both schemes exhibit the similar qualitative deficiencies. A possible explanation is the very high $y^{+}_{1}$ value and a therefore deteriorated reconstruction of the velocity gradient dU/dy for the wall shear stress. An advantage of the dual-grid system is hence the availability of an additional wall-refined grid, which yields improved wall-related coefficients. As such, Xiao and Jenny [18] reported a C_f profile taken from the auxiliary RANS simulation on the wall-refined grid, rather than from the constant-spaced LES grid. The same procedure may therefore also be viable for the present hybrid model.

Fig. 14

Skin friction coefficient C_f along the bottom wall of the periodic hill

The distribution of the mean pressure coefficient $C_{p}=\left (\langle P\rangle -P_{\text {ref}}\right )/\left (0.5\rho {U_{b}^{2}}\right )$ along the bottom and top wall, with P_ref being the mean pressure at the hill crest, is shown in Fig. 15. The hybrid simulations on both grid types are close to the reference, while the LES on the constant-spaced grid is over-predicting the pressure coefficient.

Fig. 15

Pressure coefficient C_p along the walls of the periodic hill: a bottom wall; b top wall

On the periodic hill flow, the different natures of the blending functions f_b and f_α become evident (Fig. 16). f_b is able to account for local turbulence resolution and is limited to the downstream side of the hill for the constant-spaced grid. In contrast, f_α is given for the auxiliary RANS simulation and ensures that the RANS velocity field 〈U_i〉 is used to compute $\nu _{t}^{\text {RANS}}$ (instead of the LES velocity field $\langle \overline {U}_{i}\rangle$, which is interpolated from a coarse grid) along all walls.

Fig. 16

Contours of the blending functions for the periodic hill flow near the bottom wall: af_b on the constant-spaced LES grid, bf_α on the auxiliary RANS grid

4.3 Computational cost

To estimate the additional computational time of the dual-grid hybrid RANS/LES simulations over the coarse LES on one grid, the relative overhead of the average computational time per time step was compared. Both simulation types have been run under identical conditions with maximum 24 cores (two processors with 12 cores each). For the plane channel flow, the hybrid simulations on the isotropic grid and auxiliary RANS grid have been undertaken on 23 + 1 cores, while the coarse LES have been run on 24 cores. The simulations on the wall-refined grids have been run on 7 + 1 cores (hybrid) and 8 cores (coarse LES). In average, a surplus of computational time of around 55% has been observed. The periodic hill flow has been run on 18 + 6 cores for the hybrid RANS/LES and 24 cores for the coarse LES, for which an additional time of 75% has been measured. It was found that the primary factor impacting computational time is the transfer of variables between both simulations, including the grid-to-grid interpolation. Hence, a reduction of the RANS/LES coupling to every tenth numerical time step has been tested, while the auxiliary RANS continues to run in the background. This resulted in a mere overhead of 15% against the baseline LES on the channel flow, with similar results. Further testing of this more economic modification will be part of future work.

5 Conclusion

A hybrid flow simulation method based on synchronised LES and RANS simulations, running on two distinct grids with a seamless Reynolds stress model blending model, is proposed to extend the possibility of partially resolving turbulent-structures with coarse-grid LES to high Reynolds number industrial cases. The dual-grid system, a prolongation of the underlying hybrid Two Velocity Fields model, is shown coherent with the systematic separation of the instantaneous/fluctuating flow field from the time-averaged flow field, as was practised in early 1970’s coarse LES using separate viscosities for mean flow and SGS dissipation [27]. The straddling and roaming of turbulent motions into and out of the RANS-affected near-wall layer is enabled with marginal detrimental impact on RANS and LES flow fields, as displayed by the mean, rms and spectral results, even at the first cell off the wall. The use of the additional RANS turbulence model in the hybrid SGS model is governed by a blending function, which is self-adjusting to the local resolution of turbulence by the grid resolution without reference to the wall distance. The dynamic coupling cycle including a feedback from partial-averaged LES flow field to the auxiliary RANS made both predicted fields statistically consistent. Channel flow and periodic hill test cases showed the versatility of the model for coarse LES with low resolution in wall-parallel, and also in wall-normal directions for a range of Reynolds numbers. The periodic hill flow run on deliberately very coarse grids of 0.2 and 0.8 million cells compared to the literature, produced separation and friction coefficient predictions with reasonable accuracy for industrial purposes.

Without optimisation, the computational cost to run the full hybrid model on the presented test cases is a factor 2-3 times the standalone coarse LES that yields much poorer predictions while halving its mesh step would cost 8-16 times more. Optimising load balancing across parallel computing of the RANS and LES, the extra wall-clock time is reduced to 1.75 when updating coupling terms every time step. A mere 15% extra time-delay was observed when updating these coupling terms only every ten time steps, as these partially time-averaged variables change more slowly than the resolved LES structures and make too frequent data transfer across all cores wasteful. In terms of total CPU, costs are still roughly doubled, but could be reduced if the RANS used a much larger time step than the LES, e.g. in complex geometry design applications with embedded LES.

While the presented framework is at an early stage of development, we identify additional options for further improvement, including the extension to other turbulence models such as second moment closure models. The hybrid model should be further extended to overcome the RANS/LES temperature field discrepancies, possibly by adopting an analogous temperature field blending, using more elaborate scalar flux and temperature variance models and by a Prandtl number dependency of the blending function. Ultimately, the dual-grid scheme may be developed towards an application in an “Embedded LES” context, where the LES grid is refined in flow regions of high interest, with the auxiliary RANS simulation serving for the larger domain.