Competing control scenarios in probabilistic SIR epidemics on social-contact networks

Abstract

A probabilistic approach to the epidemic evolution on realistic social-contact networks allows for characteristic differences among subjects, including the individual number and structure of social contacts, and the heterogeneity of the infection and recovery rates according to age or medical preconditions. Within our probabilistic Susceptible-Infectious-Removed (SIR) model on social-contact networks, we evaluate the infection load or activation margin of various control scenarios; by confinement, by vaccination, and by their combination. We compare the epidemic burden for subpopulations that apply competing or cooperative control strategies. The simulation experiments are conducted on randomized social-contact graphs that are designed to exhibit realistic person–person contact characteristics and which follow near homogeneous or block-localized subpopulation spreading. The scalarization method is used for the multi-objective optimization problem in which both the infection load is minimized and the extent to which each subpopulation’s control strategy preference ranking is adhered to is maximized. We obtain the compounded payoff matrices for two subpopulations that impose contrasting control strategies, each according to their proper ranked control strategy preferences. The Nash equilibria, according to each subpopulation’s compounded objective, and according to their proper ranking intensity, are discussed. Finally, the interaction effects of the control strategies are discussed and related to the type of spreading of the two subpopulations.

1 Introduction and literature review

The COVID-19 pandemic has stimulated a novel interest in models of epidemics (Bertozzi et al., 2020). Epidemiological models have guided governments and policymakers to develop policies that include measures of social distancing, lockdowns, and vaccination campaigns, all in order to control the risk of an expanding infection. Policies to minimize epidemic burden have in practice required a modulated deployment because of regional differences, behavioral obstacles, or social concerns (MacIntyre et al., 2021; Reicher & Stott, 2020). Guided by socio-political principles, specific preferences for control policies may differ in subpopulations, and optimizing the epidemic outcome under variable objectives may result in diverse—or competing—strategies in comparison to co-operative strategies. In order to assess the epidemic burden when different control strategies are deployed in subpopulations, and when each individual again could exhibit some deviating protective behavior and could express proper disease-related characteristics, a detailed population structure must be implemented in the epidemic diffusion model. Our present study, therefore, extends the classical compartmental epidemic model with a social-contact network structure at the scale of the individual, in order to encompass such individual diversities.

Starting with Kermack and McKendrick (1927), several models have been elaborated which subdivide a population into designated compartments into which individuals are allocated according to their disease status (Hethcote, 2000; Choisy et al., 2007). The classical Susceptible-Infected-Removed (SIR) approach is a basic compartmental epidemic model. In this model individuals are allocated either to the susceptible (S), the infected (I), or the removed (R) meta-population. The extensions of simple epidemic models with structured networks of individual agents (or meta-populations) (Barabási, 2013; Newman, 2018) have successfully been employed in many fields which study phenomena where interrelationships matter (Perc, 2021) and, include, biological demographic dynamics (Montagnon, 2019), international trade (Banerjee et al., 2013), technology diffusion (Eaton & Kortum, 1999), information spreading (Liu & Zhang, 2014; Li et al., 2017), corruption spreading (Kolokoltsov & Malafeyev, 2017) and contagion in financial markets (Demiris et al., 2012). In all these cases the adoption of network models has led to new perspectives and novel insights. In our present study, we develop an extension of the SIR model on social-contact networks with subpopulations adhering to competing epidemic control strategies. In previous work on infectious disease propagation, a probabilistic approach to SIS dynamics on coupled social-contact and economic production networks was explored (Broekaert & La Torre, 2021). In particular we applied the vector logistic equation on a graph for the infection-recovery dynamics to preserve the probabilistic interpretation of the S- and I-propensity of each individual node (see also Lajmanovich and Yorke 1976; Gerbeau and Lombardi 2014; Prasse et al. 2021). The adoption of a network-based approach to modeling an epidemic allows the description of patterns of interaction among individuals - the heterogeneity of the social-contact network—or to designate subpopulations with specific group properties. In a social-contact network, the links describe all person–person interactions by which the contagious disease can potentially spread. This physical contact network—based on momentarily shared locations (Barrett et al., 2009)—should be distinguished from the ‘social network’, which typically includes online besides offline relationships. Hence in general, a social-contact network spans a very different graph over a population of nodes, both by linkage structures and degrees.

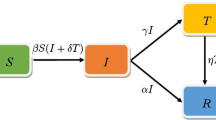
The standard SIR-approach models the evolution of an epidemic based on splitting a population into three different compartments $\{S,I,R\}$. Denoted by S are those individuals who are still untouched by the disease, and who are ‘susceptible’ to infection by contact with infected individuals. Compartment I is composed of the ‘infective’ individuals, who can transmit the disease and who can naturally or therapeutically recover from the disease. A simple assumption about infectious contacts sets it proportional to the product of the sizes of the compartments S and I (Kermack & McKendrick, 1927). Finally, in the ‘removed’ category both those individuals are allocated who have recovered and who originate from compartment I, and those who have been vaccinated and acquired immunity to the disease. The classical SIR model for the respective population fractions, $\{s,i,r\}$, reads as

$$\begin{aligned} \frac{d s}{dt} \ = \ - \beta i s, \ \ \ \ \ \ \frac{d i}{dt}= & {} \beta i s - \delta i, \ \ \ \ \ \ \frac{d r}{dt} \ = \ \delta i, \end{aligned}$$

(1)

with $\beta$ being the infection rate and $\delta$ the recovery (removal) rate of the disease for the given population. Remark that following the dynamical equation for the s fraction, the latter must be a monotonously decreasing function, and asymptotically in time the i fraction will exponentially reduce to zero. The SIR model hence always entails a recovered asymptotic outcome to an epidemic outbreak of an infectious disease.

In our present development of a SIR epidemic on a graph, we explore control scenarios that influence the progression of the epidemic at the individual level, rather than e.g. age-related meta-groups of the population as in recent work by Nakamura et al. (2021). This more detailed dynamic approach can take into account the socio-spatial distribution of individuals and the natural differences of infection and recovery capacities of each individual, and also allows the implementation of associated protective strategies for each subpopulation—or the lack thereof. Such approaches with a socio-spatial structure of the population by using complex graph topologies have been successfully developed in various domains (Keeling & Eames, 2005; Tao et al., 2006; Newman, 2002; Ganesh et al., 2005; Lu et al., 2017). In particular, our approach aims to describe the epidemic dynamics immediately at the level of the individual’s intrinsic susceptibility, infection and recovery probabilities, similar to probabilistic Markov or quantum-like system descriptions, e.g. (Busemeyer & Bruza, 2012; Wang et al., 2013; Broekaert et al., 2020; Wang et al., 2003). The probabilistic interpretation of the graph state vectors of the nodes allows the expression of any SIR-related expectation quantity on any targeted subset of nodes. The probabilistic approach then prescribes for some function f over the graph; $\langle {\textbf{f}} \rangle _{S,t}$ = $\sum _{k \in D} p_{S_k}(t) f_k$, $\langle {\textbf{f}} \rangle _{I,t}$ = $\sum _{k \in D} p_{I_k}(t) f_k$ and $\langle {\textbf{f}} \rangle _{R,t}$ = $\sum _{k \in D} p_{R_k}(t) f_k$ for the respective SIR-averages at a given time t and targeted node set D of some subpopulation.

Recent work has explored the impact of subpopulation differences, e.g. with competing features, on the epidemic evolution. The work of Guo et al. (2020) points out that subpopulations in networks, which follow different rules and have specific interactions between them, will follow asymmetric approaches—e.g. in the prisoner’s dilemma game, and this will lead to the emergence of a pattern of cyclic dominance. A Monte Carlo approach to SIR-epidemics on individual-based random hyperbolic graphs and real telephone-communication-derived graphs was tested by Gosak et al. (2021) for the effects of partial lockdowns when deployed inter, vs intra, detected communities. The study of Fan et al. (2022) implements a multiplex graph approach including a random Erdös-Rényi social-contact network for SIS epidemics and an information layer built from random simplicial complexes for disease awareness diffusion. A multi-layer approach by Peng et al. (2021) allows the inclusion of a layer of competing opinions over the network, which then influences the contagion linkages in the layer of the physical epidemic. In the work of Massaro et al. (2018) a mobility network approach is implemented with structured populations and with a specifically defined measure of system-wide critical functionality, which includes the individual infection risk and the disruption to the system’s functionality in terms of the human mobility deterioration. Our present approach of a probabilistic SIR model on a network differs in the implementation of the subpopulations which deploy competing or co-operative control strategies, and by assessing their respective outcomes through the specifically defined measure of the infection load—or the related activation margin—and the adherence to the preferences for specific control policies in each subpopulation. We first develop the probabilistic approach to SIR-dynamics on a network in the next Sect. 2, subsequently, we extend this formalism to model the epidemic burden when subpopulations deploy deviating control strategies, Sect. 3, and quantitatively assess co-operative versus competing scenarios when subpopulations express different preferences for specific control strategies, Sect. 4.

2 Probabilistic SIR-dynamics on a social-contact graph

In the probabilistic SIR model on a graph, the individuals in a population are all attributed with susceptible (S), infectious (I), and removed (R) scalable characteristics. The individuals are hence not attributed to one of the three categories by a binary exclusive membership but reveal a graded association to each characteristic. To this end, to each node state three probabilities, $p_{S_k}, p_{I_k}, p_{R_k}$, are associated which express the degree to which the given individual node, $k\in \{1,\cdots , N\}$, pertains to the respective SIR characteristic. The dynamics of the infected-component, $p_{I_k}$, is determined by the node’s individual recovery rate $\delta _k$, and by the product of its individual susceptibility, $p_{S_k}$, and all the infectivity propensities $p_{I_l}$ and infection rates $\beta _l$ of its neighbouring nodes, i.e. for which $A_{kl} = 1$, Eq. (3). The adjacency matrix A, with $A \in {\mathbb {R}}^{N,N}, A = A^T$, expresses whether two nodes, k and l, have a person–person contact $A_{kl} = 1$, or not $A_{kl} = 0$, and summarizes the basic network architecture of the social-contact graph, see e.g. Fig. 1.

With different subpopulations spread over the network, various masking operations of the adjacency matrix are required to identify intra- and inter-subpopulation linkages, and to specifically impose associated control strategies per subpopulation (see Sect. 4 and App.).

Fig. 1

Examples of two-group (red vs cyan) artificial social-contact graphs (left), $N\!\_{connect}\_A = 50$, following partially randomised homogeneous spreading (top), $skew = .5$, and block-localised spreading (bottom), $skew = .1$, and their confinement rendition (right) under co-operating confinement scenario $N\!\_{\text { confinement}}\_A = 20$ (top) and $N\!\_{\text { confinement}} = 10$ (bottom). In the unconstrained graphs the mean degree is 57.76, respectively 96.2. In the confined graphs the mean degree has respectively decreased to an average of 14.65 and 9.45 remaining contacts. The node-coloring scheme allows to control the extent of inter-group boundary contacts (bottom) and the homogeneity of the spreading (top) (Color figure online)

The individual infection and recovery rate vectors, ${\varvec{\beta }}$ and ${\varvec{\delta }}$, can either be realistically allocated (when such information is available) or randomly attributed following a lognormal distribution. In the latter case a parametrization is required according to a mean infection rate $\beta _{\text { avg}}$, a mean recovery rate $\delta _{\text { avg}}$ and their respective standard deviations.¹ The probabilistic SIR model in terms of individual nodes has the susceptible-component, $p_{S_k}$, of node k evolve decreasingly according to a $\beta$-weighted product with its neighboring nodes’ infective components, Eq. (2) (normalized with its degree $d_k$). Additionally, this component can evolve by a vaccination intervention, $V_k$. In our model, the vaccination of the randomly chosen node k at some instant of time, resets the susceptible component to a small value related to the vaccine’s efficiency, Eq. (7). The removed component, $p_{R_k}$, evolves increasingly according to node k’s natural or therapeutic recovery rate $\delta _k$ from its infectious component, Eq. (4), and when occurring, by vaccination intervention, $V_k$. The vaccination of a node resets its removed component mainly to the value of the vaccine’s efficiency, Eq. (7). The infected-component, $p_{I_k}$, of node k evolves according the balance of recovery and infection, Eq. (3), and is reset to zero when vaccination occurs, Eq. (7). The diffusion of the epidemic over the graph ${\mathscr {G}}_A(V,E_A)$ with SIR dynamics and stochastic vaccination is thus given by²

$$\begin{aligned} {{\dot{\textbf{p}}}_S}= & {} \left\{ - {\textbf{p}_S} \circ {\textbf{d}}^{-1} \circ A_t\, \beta \, {\textbf{p}_I}, {\textbf{V}}_{rand.} \right\} , \end{aligned}$$

(2)

$$\begin{aligned} {{\dot{\textbf{p}}}_I}= & {} \left\{ - \varvec{\delta } \circ {\textbf{p}_I} + {\textbf{p}_S} \circ {\textbf{d}}^{-1} \circ A_t\, \beta \, {\textbf{p}_I}, {\textbf{V}}_{rand.} \right\} , \end{aligned}$$

(3)

$$\begin{aligned} {{\dot{\textbf{p}}}_R}= & {} \left\{ \varvec{\delta } \circ {\textbf{p}_I}, {\textbf{V}}_{rand.} \right\} , \end{aligned}$$

(4)

where $A_t$ indicates the time-epoch dependent adjacency matrix which can result from the temporary confinement strategies in the network. Note that $\dot{p}_{S_j}+\dot{p}_{I_j}+\dot{p}_{R_j}= 0$ for all j, over the continuous time evolution and the stochastic vaccination operation, Eq. (7). This ascertains the conservation of the value of the summed components. With initial conditions $p_{S_j}(0)+ p_{I_j}(0)+ p_{R_j}(0)= p_{S_{j,0}}+ p_{I_{j,0}}+ p_{R_{j,0}}= 1$, the sum of SIR-components in each node remains equal to 1. One further notices if $p_{I_k} = 1$, then $p_{S_k} = 0$ and $\dot{p}_{I_k} = - \delta _k$ shows a decreasing I component. While, if $p_{I_k} = 0$ and if $p_{S_k} \geqslant 0$, then $\dot{p}_{I_k} = p_{S_k} {d_k}^{-1} A_{kj} \beta _j p_{I_j}$ which shows an increasing I component. This ascertains $p_{I_j} (t) \in [0,1]$ at all times. With non-negative SIR-components, the $p_{S_k}$ are monotonically decreasing and $p_{R_k}$ monotonically increasing—except instantaneously at the moment of the vaccination re-set, see Eq. (7). If $p_{R_k} = 1$ then $p_{S_k} = 0$, $p_{I_k} = 0$ and $\dot{p}_{R_k} = 0$, hence the $p_{R_k}$ component has reached its maximum value. Similarly, if $p_{S_k} = 0$ then $\dot{p}_{S_k} = 0$ and its lowest value is reached. In sum, the components of each node state $(p_{S_k}, p_{I_k}, p_{R_k})$ on the social graph satisfy the property of probabilities, which allows a consistent probabilistic interpretation of the graph-based SIR dynamics with vaccination and confinement, Eqs. (2, 3, 4, 7), (Lajmanovich & Yorke, 1976; Gerbeau & Lombardi, 2014; Prasse et al., 2021; Broekaert & La Torre, 2021).

The rendition of each individual node’s SIR-state over time allows comparing in detail the epidemic burden resulting from various control scenarios. In particular the effectiveness of the control scenarios will be quantified by their resulting infection load ($I\!L$) or activation margin (AM), defined as

(5)

(6)

Notice that both measures require solving the temporal evolution of SIR-state for each individual node in the graph, Eqs. (2, 3, 4). Both measures provide an assessment of the disease’s impact on each individual over the full time-range of the epidemic. This is in contrast with an impact measure of an epidemic outbreak which would report the maximum value of the average infection probability over time, . The infection load reports a cumulative effect of the epidemic by compounding the possible worst infection impact on each individual. The infection load, Eq. (6), hence provides an upper bound to the maximal population infection and gives a measure of the longitudinal impact of the epidemic.³ Similarly, the activation margin—as defined in Eq. (6)—compounds the lowest ‘fitness level’ of each individual during the epidemic, and hence it reduces to the complement of the infection load.

3 Competing and co-operative control scenarios in subpopulations

The epidemic burden of an infectious disease can be partially controlled by deploying policies of social distancing, lockdowns, curfews, and targeted or generalized vaccination campaigns. In order to capture the effect of such policies, epidemic models have included formalisms, for e.g. vaccination, shield immunity or quarantine control in a compartmental SEIR-model (Xu et al., 2021), or hierarchical quarantine control (Yang, 2021). In our present model, we implement both confinement and vaccination control strategies and their combination. Furthermore, we allow distinct control strategies for each subpopulation and will consider two variants of the topological spreading of the subpopulations over the social-contact graph. Under competing strategies, the optimal control scenario is derived form the Nash-Equilibrium in the pay-off matrix, e.g. Table 6, of the objective metric, Eq. (16). These basic game-theoretic notions are concisely reviewed at the end of this section.

Confinement. In our model we will define the confinement approach as any set of measures that results in less contagious transmission of the disease, including e.g.; restricted public hours or perimeters, social distancing, sanitary mask-wearing, or restricted contact bubbles. The goal of this control measure is to reduce the number of infections and the number of infected individuals through natural and therapeutic recovery, at the end of the confinement time window. The control strategy by confinement is implemented in the graph model by replacing—during a pre-defined window of time—the adjacency matrix, A, parametrized with the threshold connection parameter (N_connect_A), by the culled adjacency matrix, A_confinement, in which the connection parameter has been lowered (N_confinement_A), see Fig. 2. In the case of a competing confinement control scenario, the adjacency matrix receives an adjusted threshold mask for the confined subpopulation only, and only so for the duration of the confinement period (see App.).

Fig. 2

The heavy-tailed degree distribution of the random artificial social-contact graph ${\mathscr {G}}_A(V,E_A)$ of Fig. 1, in unrestricted setting (left), and during confinement ${\mathscr {G}}_{A_{conf}}(V,E_{A_{conf}})$ (right), exhibiting differences in ego-networks and variable compliance with confinement regulation by the individual nodes

Vaccination. The control strategy by vaccination is implemented in the dynamics, Eqs. (2, 3, 4), according to a stochastic operation, Eq. (7), starting at a defined initial time point and running till the full supply of the vaccines is administered. We make a simplifying assumption, that by its vaccination any node with SIR probability state $(p_S,p_I,p_R)$ will reduce to a weighted linear combination with the optimally vaccinated SIR-state $\left( 1-e,0,e\right)$ at the instance of administration,

$$\begin{aligned} {\textbf{V}}_{\mathrm{rand.}}: \qquad \begin{pmatrix} p_S\\ p_I\\ p_R\end{pmatrix}_{\!\!\! t+dt} = e\begin{pmatrix} 1\!-\!e\\ 0\\ e\end{pmatrix} + (1-e)\begin{pmatrix} p_S\\ p_I\\ p_R\end{pmatrix}_{\!\!\! t}, \end{aligned}$$

(7)

where e is the efficiency of the vaccination treatment, $e \in [0,1]$. This operation conserves the unit value of the total probability mass in each node. A high vaccination efficiency will set the SIR-state pre-dominantly in the recovered mode, while a small remaining susceptible component allows for possible breakthrough infections to occur. When the vaccination is largely ineffective, $e\approx 0$, the SIR-state remains essentially unchanged. This operation implies that all types of nodes are vaccinated, even if the probability for R or I is higher than the probability for S. The model further assumes a node is vaccinated only once at most. In practice, after a pre-defined number (lag) of time steps a fixed number (vacc_batch) of randomly chosen nodes is vaccinated, and the other non-vaccinated nodes and earlier vaccinated nodes continue to evolve according to the continuous-time SIR dynamics without any vaccination operation. The time lag of administration, the phased batch size, and the total amount of vaccines allow modeling the vaccination strategy with a realistic slower deployment in comparison to confinement strategies of shorter duration. In the case of competing vaccination control scenarios, the population is masked to only target the concerned subpopulation. When only one of the subpopulations deploys a vaccination control strategy, the full administration capacity is applied to this subpopulation. When more subpopulations choose the vaccination strategy, the administration capacity remains fixed for the whole population. A joint vaccination strategy with full availability of vaccines for the whole population hence spreads the fixed administration capacity over all the subpopulations, and thus leads to a smaller number of individuals in each group receiving the vaccination at each lagged time instance, and requires a longer time period to vaccinate the whole population.

Subpopulations topology. The structuring of subpopulations in a random contact-graph can be implemented according to a number of guiding principles. In our present study, we include both structuring based on homogeneous spreading—e.g. differences due to political inclination, and block localization of subpopulations—e.g. differences due to geographical concentration. To validly compare the epidemic burden of various control scenarios we maintained an equal size for the subpopulations. The configuration with the homogeneous subpopulation spreading was derived by labeling the nodes along the adjacency diagonal with consecutive group indices repeatedly.⁴ A more realistic graph adjacency is subsequently obtained by the random partial shuffling of the node group labels.⁵

Subpopulation control policy preferences. Socio-political differences in populations (see e.g. Gros et al. 2021), or subpopulations, lead to the implementation of different control policies. In our present study, we compound the main objective of a decrease of the infection load, due to the implemented control strategy, with its proxy cost related to its preference ranking and the intensity of this ranking. In the present context, we fix the control strategies in an ad hoc order

$$\begin{aligned} C\!S = [ \, \text {none},\ \text {confinement},\ \text {vaccination},\ \text {confinement and vaccination} \, ] \end{aligned}$$

(8)

relative to which, for each subpopulation, the preferred rank of control strategies is denoted. In particular, we define two artificial contrasting subpopulations according to their difference in policy preference ranking, e.g. Allcott et al. (2020):

$$\begin{aligned} O_0 \ = \ \left[ 1, 2, 3, 4 \right] ,&\ \ \ \&O_1 \ = \ \left[ 4, 2, 1, 3 \right] . \end{aligned}$$

(9)

Out of a continuum of possible policy rankings, we selected these two hypothetical profiles which evoke a clear degree of partisanship or polarisation, and of which variations do occur in real-world socio-political situations (Deane et al., 2021; Schaeffer, 2021). The policy ranking profile, $O_1$, of the ‘1-group’, vacc. $\succ$ conf. $\succ$ conf.$\_$vacc. $\succ$ none, expresses a preference for medical intervention prior to a social effort to diminish transmission and which favors the deployment of a control policy. In contrast, the profile $O_0$ of the ‘0-group’, none $\succ$ conf. $\succ$ vacc. $\succ$ conf.$\_$vacc., expresses a preference for a ‘hands-off’ approach, with the deployment of a medical intervention strategy only in last resort. A measure of nuance to the policy preferences is provided by retaining an ‘intensity’, I, for the provided ranking. We note that in reality individuals in each group will show heterogeneity in their preference ranking. In our approach, we have reduced this underlying variety to a typical and hypothetical ranking that characterizes each of these two respective groups, Eq. (9). One can however also interpret the policy ranking for each of these subpopulations as a top-down decision by their respective policymakers. This approach reduces the joint or competing strategy scenarios to a 2-player game –instead of a 1000-player game– which is sensible in the deployment of control strategies like confinement regulation and grand-scale vaccination programs. Notice, that agents do still express their individualism through e.g. personal connectivity to others, Fig. 2. A quantification method for the utility of ranked criteria has been developed in the context of ‘multi-decision maker’ theory, e.g. by Zhang et al. (2004) and Herrera et al. (2001), and extends the models of Luce and Suppes (1965). These models allow the transformation of a preference ranking into multiplicative weights that can be compounded with—in our present case—the infection load, given the intensities, $I_0$ or $I_1$, of these rankings. Using Saaty’s 1-to-9 magnitude scale, with ‘9’ indicating an absolute preference for one over another alternative, and ‘1’ indicating the indifference of preference between the two alternatives, the deployment of the competitive control scenarios in the two subpopulations can be assessed at different levels of socio-political primacy (Saaty, 1978). The multiplicative weighting scheme for the four ($n=4$) alternative policies, with intensity I, follows

$$\begin{aligned} w(i)= & {} \frac{\Pi _{j=1}^n \tau _{ij}^{1/(n-1)}}{\sum _{i=1}^n \Pi _{j=1}^n \tau _{ij}^{1/(n-1)}}, \end{aligned}$$

(10)

with $\tau _{ij} = I^{\Delta _{ij}}$ and $\Delta _{ij} = (O_1(i) - O_0(j))/(n-1)$, (Zhang et al., 2004). The weight vectors, $w_0(i)$ and $w_1(i)$, of the policy rankings, Eq. 9, make up the elements of the policy-based component of the compounded payoff matrix, Sect. 4.3, Appendix B and Appendix C.

3.1 A game-theoretic perspective on joint epidemic control strategies

The outcomes of the epidemic mitigation efforts by various policymakers are interdependent. The goal-effectiveness of each group’s chosen control strategy depends on the other group’s strategy due to the epidemic diffusion between the groups. From a game-theoretic perspective, these strategic interactions among two rational agents are represented in a game matrix (Nash, 1950; Myerson, 1991; Rajiv & Jörgen, 2016). For two players, the pure strategy profiles $\{s_0,s_1\}$, composed of the two players’ respective competing strategies $s_0,s_1 \in C\!S$, Eq. (8), condition the entries of the full game matrix $C\!S\!\times \!C\!S$ comprising all strategy profiles. The dual entries of the game matrix are given by the compounded goal function value ${P_C}_i (\{s_0,s_1\})$, Eq. (16), for each player $i \in \{0,1\}$.⁶ In this particular setting, each player aims to minimize their proper compounded cost. In order to describe a state that is preferred by all players, we first define the strategy profile , in which player i’s strategy is replaced by $t_i$ and the other’s strategy is maintained (Rajiv & Jörgen, 2016). Then, an equilibrium strategy profile $\{s_0^\star ,s_1^\star \} \in C\!S\!\times \! C\!S$ exists, when for $\forall i \in \{0,1\}$, and all strategies $t_i \in C\!S$,

(11)

This Nash Equilibrium, $\{s_0^\star ,s_1^\star \}$, is hence a strategy profile at an equilibrium point from which neither player can improve their outcome by unilaterally switching to a different strategy. A Nash equilibrium need not always exist in a pure strategy game. In a mixed strategy game, where probabilities are allocated over pure strategies, it can be proven there always exists a mixed Nash equilibrium (Nash, 1951). Moreover, the game-theoretic approach assumes both policymakers use shared predictive epidemic models, communicate their intentions and will deploy their respective strategies consistently.

A practical method to identify the Nash equilibrium in the pay-off matrix is to verify if the first value in the dual entry is the minimum in its column (i.e. over the possible strategies of group-0), and if the second value is the minimum of its row (i.e. over the possible strategies of group-1). In the pay-off matrix for the compounded objective, Table 6, this method easily identifies two Nash equilibria.

With differing epidemic progression in the subpopulations under their respective control strategies, we can now gain insight into how these deviating control scenarios impact the proper group and how these strategies cross-interact. We first implement co-operative control scenarios—i.e. in which all nodes are subject to the same sanitary control strategy—and assess the epidemic burden according to the infection load. Subsequently, we will assess the epidemic infection load for subpopulations deploying deviating control scenarios, Sect. 4.2. With a complete infection-load-based pay-off matrix in place, thereafter the effect of compounding the objective with differing policy preferences can be assessed, Sect. 4.3. To efficiently compare the effect of control scenarios we will implement a competitive model with two subpopulations of equal size.

4 Implementation and simulation results

The network architecture plays a major role in the diffusion and amplitude of an epidemic (Ganesh et al., 2005). The social-contact network in our present study was built as a partially sorted random-based social-contact graph (Broekaert & La Torre, 2021). The implementation with partial sorting of the initial random probability of a connection between two nodes allows more realistic aspects of true person–person networks, similar to those that have been reconstructed by e.g. Barrett et al. (2009). The resulting adjacency matrix, A, of the graph enhances the number of cliques and clustering in the graph and produces a heavy-tailed degree distribution, Fig. 2. The graph is parametrized by the connection number ($N\!\_connect\_A$) to tweak the number of contacts, and the ‘order variable’ (skew) which weights the degree of randomness of adjacencies in the graph. An effective connection between two nodes is established if the connection probability is equal to or larger than a given threshold, which depends on the confinement parameters imposed by each subpopulation (details appear in the Appendix). Finally, a weighting procedure on sorted and unsorted connection probabilities with a skew-parameter allows to adjust for clustering degree in the graph, App. Eq. (A.1).

In our simulations experiments we fixed the population size ($N=1000$), and the unconstrained connectivity ($N\!\_connect\_A = 50$). When subpopulations follow competing control strategies partial maskings of the adjacency matrix for intra and inter subpopulation linkages are used to reconfigure the temporary adjacencies in the dynamics, Eqs. (2–4). Individuals belonging to the same subpopulation connect according to their associated confinement strategy. For the inter subpopulation linkages, a negotiated connection parameter is used, which equals the average of both subpopulation’s connection parameters, App. Eq. (A.2). For each random social graph in the simulations Experiment 1 and Experiment 2—e.g. Fig. 1 and its degree distribution, Fig. 2—fixed epidemic parameters have been used. In particular, we implemented an epidemic with random lognormal distributed individual infection rates $\beta _{\text { avg}} = .08$ ($\beta _{\textrm{SD}}$ = .05) and recovery rates $\delta _{\text { avg}} = .2$ ($\delta _{\textrm{SD}}$ = .05), and with 50 infected nodes ($init\_\text { infected}$) at start.⁷ Hence, the subpopulations have not been differentiated with respect to the epidemic parameters but solely according to their deployed control strategy.

We can then assess the effect of the confinement strategy, vaccination strategy, and combined vaccination-confinement strategy, by comparing their resulting infection load, Eq. (6), with its base-value in the no-control strategy.

The vaccination strategy will take a random selection of nodes from the vaccination start time and will reset this fixed number of nodes (vacc_batch) to the vaccinated state, Eq. (7), and repeat each fixed number of time steps (lag) till the vaccine supply ($vacc\_tot$) is finished.

For nodes on which no vaccination operation is completed at a given time instance, the SIR dynamics, Eqs. (2, 3, 4), reduces to a system of first-order vector differential equations which allow an iterative numerical solution. Following an initialisation of the SIR-states $\mathbf {p_S} (0) = \mathbf {p_S}_0$, $\mathbf {p_I} (0) = \mathbf {p_I}_0$ and $\mathbf {p_R} (0) = \mathbf {p_R}_0$ an incrementally updated solution is obtained through the operation of an iteratively updated propagator;⁸

$$\begin{aligned} \mathbf {p_S} (t+dt)= & {} \mathbf {p_S} (t) - dt \, \mathbf {p_S}(t) \circ {\textbf{d}}^{-1} \circ A(t) \beta \, \mathbf {p_I}(t) \end{aligned}$$

(12)

$$\begin{aligned} \mathbf {p_I} (t+dt)= & {} ({\textbf{1}}-dt \,{\varvec{\delta }}) \circ \mathbf {p_I}(t) + dt \, \mathbf {p_S}(t) \circ {\textbf{d}}^{-1} \circ A(t) \beta \, \mathbf {p_I}(t) \end{aligned}$$

(13)

$$\begin{aligned} \mathbf {p_R} (t+dt)= & {} \mathbf {p_R}(t) + dt \,{\varvec{\delta }} \circ \mathbf {p_I}(t) \end{aligned}$$

(14)

In order to compare the effectiveness of the vaccination control and the confinement control and their combination, we assess the epidemic burden for co-operative scenarios in simulation Experiment 1, (Sect. 4.1). The configurations with subpopulations that deploy competing scenarios are assessed in Experiment 2, (Sect. 4.2). All scenarios are finally assessed according to the compounded objective of the infection load reduction and a measure of adherence to the preference ranking of the control strategy, (Sect. 4.3)

4.1 Co-operative control scenarios for the single objective of infection load reduction

For Experiment 1, we note that with the fixed configuration of the social graph type and epidemic, Fig. 1, a maximal graph-averaged infection is reached for $t \approx 200$ when ‘no control’ is deployed, Fig. 3. With respect to this observation, our study proposes three confinement strategies that imply the same proxy cost as implied by the duration (steps_conf_duration), and the severity of the confinement, (N_confinement_A) but only differ by their starting point in time; ‘Early’, ‘Mid’ and ‘Late’ (steps_conf_start = 100, 200, 300 respectively).

For the vaccination strategies we have explored three deployments that again imply the same proxy cost as implied by the total number of 1000 vaccines, (vacc_tot), and a number of 10 administered vaccines (vacc_batch) at the start of each next lag of 6 time steps (steps_vacc_lag). Also, the effectiveness of the vaccine, $e = .9$, is kept fixed, and again the only difference is the starting point of the vaccination campaign in time, ‘Early’, ‘Mid’, or ‘Late’. With the given parameters, the vaccination campaign can cover the full population and requires 600 time steps (steps_vacc_duration) to complete. A configuration with limited availability of doses can be derived from the competing control scenarios in Experiment 2.

For the combined vaccination-confinement strategies we have—to simplify comparison—superposed the corresponding separate vaccination and confinement strategies. The simulation experiment ($n_{\textrm{iter}} = 50$) reveals that the basic control strategies show a strong dependence of the epidemic burden on the starting time point of intervention with respect to a presupposed peak of the epidemic, see Table 1. The implemented confinement strategy and vaccination strategy show a clear gain in the infection load for the former strategy, $-.159$ versus $-.037$. If no interaction of the strategies occurs the combined strategy is expected to deliver a gain equal to the sum of gains of the two separate strategies. The observed gain from the combined confinement-vaccination strategy at $-.238$ shows a significant non-additive interaction of the two control components to the size of $-.042$. Given that the control strategies would come at the same proxy cost and the observation of an increasing infection load with starting time, Table 1, the guideline is to intervene as early as possible with the epidemic control policy and to prefer the synergy of a combined confinement-vaccination strategy above a plain confinement strategy which proves more effective than the plain vaccination strategy in this implemented type of SIR-epidemic.

Fig. 3

Uncontrolled SIR epidemic. An illustrative SIR-epidemic evolution on a random social-contact graph ${\mathcal {G}}(V,E_A)$ with 1000 nodes (N), 50 initially infected nodes (init$\_$infected), and an average social connectivity parameter set at 50 (N$\_connect$_A) causing a .601 infection load. The individual connectivity degree, infection and recovery rates allow a fine-grained analysis of SIR-state progression (top panels) in comparison to its mean-field and variance rendition (bottom panels). In particular the individual SIR-course over time of the initially infected and the initially susceptible nodes can be distinguished, and inform the variance in the epidemic SIR-metrics

Table 1 The averaged infection load and standard deviation, Eq. (6), in nine basic control strategies uniformly applied on random social-contact graphs ${\mathcal {G}}_A(V,E_A)$, of type Fig. 1, with SIR-epidemic, of type Fig. 3 (minimum I-load in boldface)

Fig. 4

Co-operative controlled SIR epidemic. The relative optimal control strategy of ‘early’ combination of vaccination and confinement on the SIR-epidemic, Fig. 3, for the random social-contact graph ${\mathcal {G}}_A(V,E_A)$, Fig. 1, results in an infection load of .36, reduced from .601 without control strategy, Table 1. SIR-state progression (top panels) in comparison to its mean-field and variance rendition (bottom panels). Vaccination and confinement start at time step 100. The confinement reduces the contact parameter from 50 to 20 for a duration of 200 steps. The vaccination randomly selects 10 nodes every 6 time steps and ends after 600 steps with the depletion of the 1000 available doses. The node-based controlled epidemic evolution (top panels) reveals the longitudinal occurrence of the maximal individual Infectious components which contribute to the $I\!L$-metric of the epidemic

4.2 Competing control scenarios for the single objective of infection load reduction

The epidemic burden is highly dependent on the parameters of a control strategy, it is, therefore, crucial to insert the specific constraints of the strategies that are in place in the different subpopulations of the network. The effect and cross-interaction of deviating scenarios will moreover depend on the topological spreading of the subpopulations over the random contact-graph. In our present study, we include both; configurations based on a homogeneous spreading and configurations based on a block localization of the subpopulations. These two subpopulation configurations are adapted to respectively model individual differences that can often be considered independent of geographical location within a community—like political inclination or age group, versus individual differences that do depend on location like regional constituency or national identities. The effect of deviating control scenarios is now assessed by applying subpopulation masks to the population in order to obtain group-specific infection loads.

In simulation Experiment 2 all the possible competitive and co-operative strategies of confinement, vaccination, confinement-vaccination, or no-control are assessed for two subpopulations. Given the effectiveness of the tested control strategies in Experiment 1, Table 1, the ‘Early’ time setting is retained. Further, we let the vaccine be available for the full population ($vacc\_tot$ = 1000), since a no-vaccination strategy can be adhered to by a subpopulation.

Table 2 The pay-off matrix, $P_{\textit{IL}}$, of the averaged infection load change—with respect to the infection load .602 of the No$_0$-No$_1$ co-operative scenario—for competing two-group control scenarios with partially shuffled-homogeneous group spreading in random social-contact graphs ${\mathcal {G}}_A(V,E_A)$, ($n_{\textrm{iter}} = 50$, SD $\approx$ .003–.007) (largest I-load decrease in boldface)

The major observations for the control scenarios with the homogeneous spreading of the two subpopulations are given by the pay-off matrix of the group-specific infection load change, with respect to the no-control configuration, Table 2. We note that even though the social-contact networks are generated in a partially random process (see Appendix), the pay-off matrices Table 2 are symmetric for both subpopulations. Possible asymmetric infection loads on subpopulations, due to differences in their respective network structure, have been averaged out by aggregation over, $n_{iter}=50$ random social-contact networks.

First; the optimal control solution and the Nash equilibrium in the minimization of the epidemic burden by the two subpopulations are to deploy a co-operative Confinement-Vaccination strategy, Conf-Vacc$_0$-Conf-Vacc$_1$, resulting in a $-.238$ decrease of the infection load for both subpopulations. Neither subpopulation can improve its proper infection load without increasing the other subpopulation’s infection load. Other co-operative strategies are less opportune, conforming to the observations in Experiment 1. Second; a strong between-group interaction is apparent in the epidemic load. When one subpopulation changes strategy this affects the epidemic burden not only for the in-group but also for the out-group. Because of the abundant between-group adjacencies, the deviating control scenarios frequently inject relatively exogenous SIR-levels in each subpopulation. This is most visible in the competing scenario when one subpopulation holds on to the no-control strategy and it still benefits from an epidemic burden improvement of $-.063$ in No$_0$_Conf$_1$, $-.020$ in No$_0$_Vacc$_1$ and $-0.078$ in No$_0$_Conf-Vacc$_1$, which is due to the control efforts of the other group. For the controlling subpopulation, the effectiveness of their control effort has concomitantly weakened by $+.025$, $+.017$, and $+.047$ on the group’s infection load (w.r.t co-operation). Third; we note that the interaction of the control strategies has essentially weakened in the competitive scenarios.⁹ We point out that the competitive configurations with No$_0$ in which the counter strategies result in $-.135$ for Conf$_1$, $-.054$ for Vacc$_{1}$ separately, and $-.191$ for Conf-Vacc$_1$ combined, which shows an insignificant interaction gain of $-.002$ on the infection load.

Finally, we point out the competitive scenario with joint confinement strategy, Conf$_0$-Conf-Vacc$_1$ which shows the second-best decrease of infection load outcome at $-.220$ for the confining group and $-.254$ for the confining-vaccinating group, and which represents the best in-group improvement of the infection load overall strategies. The improved infection load for the out-group w.r.t to the Nash joint confinement-vaccination strategy is related to the limited capacity of the vaccine administration fixed in the model. In the competing scenario, the fixed vaccine administration capacity (10 subjects per lag of 6 time steps) is allocated to a single subpopulation which leads to the full number of individuals vaccinated per instance and a shorter time to cover the whole subpopulation. When both subpopulations share the limited capacity of vaccination administration, its implementation becomes less effective.

A part of the control interaction effect and also the in-group effectiveness of control strategies should be related to the particular adjacencies of the near homogeneous mixing of the subpopulations. In the second installment of Experiment 2, a block-localized spreading of the two subpopulations is used which can clarify the impact of subpopulation topology on the effectiveness of control scenarios.

Table 3 The pay-off matrix, $P_{\textit{IL}}$, of the averaged infection load change—with respect to the infection load .602 of the No$_0$-No$_1$ co-operative scenario, in competing two-group control scenarios with partially shuffled block-localised group spreading in random social-contact graphs ${\mathcal {G}}_A(V,E_A)$, $n_{\textrm{iter}} = 50$, SD $\approx$ 0.005–0.02)

The observations in the competing control scenarios with the block-localized spreading of the two subpopulations are again derived from the pay-off matrix of the group-specific infection load changes, Table 3. First, we observe the optimal control solution and the Nash equilibrium in the minimization of the epidemic burden by the two subpopulations, which is again to deploy a co-operating Conf-Vacc$_0$-Conf-Vacc$_1$ strategy by both subpopulations, leading to a gain of $-.238$ on the infection load. Further, we observe that due to the partial geographical separation, much less effect from the outside group’s strategy is sustained, while the cross-interaction of the within-group strategy is more prominent again. A gain of $-.160$ on the infection load is reached by confinement, and $-.068$ is reached by vaccination, which shows an interaction gain of $-.022$ in the infection load of $-.250$ when the strategies are combined. For the in-group, without any control strategy, all these out-group strategies have marginally no impact anymore on the in-group infection load. The latter is an immediate consequence of the partial geographic isolation of the two subpopulations.

4.3 Control scenarios compounding the infection load reduction and the policy preference ranking

The deployment of epidemic control strategies is dependent on population socio-political factors in policy-making (MacIntyre et al., 2021; Reicher & Stott, 2020). In our approach, the compounding method inserts a socio-political penalty to implementing a policy that is not preferred by the subpopulation, which alternatively can also be defined as a proxy cost in each subpopulation for deploying their respective control policies. From the policy rankings of the respective subpopulations, $O_{0}$ and $O_{1}$, the ranking weights $w_{i[j]}$ can be obtained following the multiplicative weights method, Eq. (9). More details about the multiplicative weighting scheme and the pseudo-code are given in Appendix B and Appendix C. These weights are used to express the perceived utility of each control measure (in the order of (8)) and constitute the entries of the policy ranking pay-off matrix $P_{\textit{PR}_{ij}} = [w_0(I_0)_i\,, w_1(I_1)_j]$, or explicitly¹⁰

(15)

The policymaker needs to balance the socio-political preference ranking with the concomitant epidemic outcomes. The two-pronged answerability is aggregated by considering a ranking of both objectives. Two perspectives are assessed, one in which the minimization of the infection load ($I\!L$) is ranked higher than the adherence to the control policy preference ranking (PR), with $O_{\textit{IL},\textit{PR}} = [1, 2]$ and the second perspective in which the minimization of the infection load and the adherence to the control policy preference ranking are equally valued $O_{\textit{IL},\textit{PR}} = [1,1]$. This ranking is again translated into weighting $[\theta _1, \theta _2]$, using the multiplicative weights method, Eq. (10).¹¹ The compounded pay-off matrix, $P_C$, for the weighted objectives can then be obtained as

$$\begin{aligned} P_C&= \theta _1 P_{\textit{IL}} - \theta _2 P_{\textit{PR}}, \end{aligned}$$

(16)

where the infection load payoff matrix, $P_{\textit{IL}}$, is derived from Table 2 (or Table 3 for block-localisation). Notice that the component of policy preference weight $P_{\textit{PR}}$ diminishes the compounded impact measure in an overall minimization goal.

With different control policy preferences in both subpopulations, the Nash equilibrium can shift away from the co-operative Conf-Vacc$_0$-Conf-Vacc$_1$ strategy, Tables 2, 3. Depending on the policy ranking preferences ($O_0$ and $O_1$) and their intensities ($I_0$ and $I_1$) in each subpopulation, the priority of the objectives of infection load reduction and policy preference or proxy cost ($O_{\textit{IL},\textit{PR}}$), and the type of population spread (homogeneous vs block-localised); the Nash Equilibrium will move across the respective payoff matrices, $P_C$. Because of these multiple contingent parameters impacting the optimal response to the epidemic, Tables 4 and 5 now report the Nash Equilibria strategies over ranges of ranking intensities. From the Nash Equilibria, Tables 4 and 5, one observes more scenario variability in the case of a homogeneous spreading of subpopulations. This observation confirms the increased mutual effect of the competing control policies due to the higher number of between-group contacts in this type of spreading. In the homogeneous spreading configuration, the effect of an increased policy ranking intensity moves the Nash Equilibrium towards a competitive strategy in which the proper chosen strategy has a higher preference. The latter effect is more outspoken when the objective of the infection load is weighted on a par with the policy preference ranking, $O_{\textit{IL},\textit{PR}} = [1, 1]$. In the socially more acceptable prioritisation of minimizing the infection load above adhering to policy ranking preference, $O_{\textit{IL},\textit{PR}} = [1, 2]$, the effect of partisanship is less diverse, but still results in a competitive Nash equilibrium of Conf$_0$-Conf-Vacc$_1$ strategies (top versus lower panels of Tables  4 and 5).

Table 4 The Nash equilibria dependency on the intensity of the control policy ranking in two subpopulations, with homogeneous subpopulation spreading, equal weighting $O_{\textit{IL},\textit{PR}} = [1, 1]$ (bottom panel) or epidemic priority weighting $O_{\textit{IL},\textit{PR}} = [1, 2]$ (top panel), of the infection load objective over the policy preference ranking

Table 5 The Nash equilibria dependency on the intensity of the control policy ranking in two subpopulations, with block-localised subpopulation spreading, equal weighting $O_{\textit{IL},\textit{PR}} = [1, 1]$ (bottom panel) or epidemic priority weighting $O_{\textit{IL},\textit{PR}} = [1, 2]$ (top panel), of the infection load objective over the policy preference ranking

Finally, we note the special case with an equal policy ranking intensity ‘3’ in both subpopulations, with homogeneous spreading, with equal weighting of the infection load objective and policy preference ranking, which leads to a payoff matrix, Table 6, with two Nash equilibria. In this particular configuration, the two subpopulations can take recourse to either of the two competitive control scenarios Conf-Vacc$_0$-Conf$_1$ or Conf$_0$-Conf-Vacc$_1$.

Table 6 The compounded payoff matrix $P_{\textit{C}}$ (for configuration ‘3$\_$3$\_$5$\_$hom$\_$11’) for an equal policy ranking intensity, $I_0 = I_1 =3$, in both groups, with homogeneous spreading of the two subpopulations and with equal weighting of the infection load objective and policy preference ranking, $O_{\textit{IL},\textit{PR}} = [1, 1]$, at ranking intensity $I\! =\! 5$, exhibits two Nash equilibria (in boldface)

5 Discussion and conclusion

Stemming from possible cooperative or non-cooperative control strategies, a game strategic perspective underlies our epidemic model. Our study explored epidemic outcomes when two subpopulations can separately decide to deploy temporary confinement, a vaccination program, or a combination of both. Technically, the subpopulations were spread over a realistically designed social-contact graph which allows a heterogeneous individual-based description of the epidemic impact. The probabilistic state description of the individual nodes—which extends the stochastic SIR epidemic approach to diffusion on graphs—allows deriving SIR-values continuously over time. The individual-based longitudinal infection probability was used to define the Infection Load metric that enables monitoring the average of the worst impact on each individual over the full duration of the epidemic. In particular, in our model, each subpopulation aims to optimize a compound metric consisting of their Infection Load and adherence to their control policy-related socio-political objectives. A basic comparison of co-operative vaccination and confinement scenarios was carried out to explore the effects of these control strategies in relation to their economic proxy cost from the total amount of administered vaccine doses, the reduction of the number of social contacts, and the onset time of the confinement. A multiple testing approach on designed random graphs indicates, first, the earliest onset time of interventions results in the lowest infection load on the social-contact graph, and second, the combination of the strategies of vaccination and confinement of the population in the social-contact graph results in the lowest infection load. A clear interaction effect of control strategies is observed. The combined effect of vaccination and confinement surpasses the sum of both strategies separately. Under competing strategies between subpopulations this interaction effect is mostly lost in the homogeneous mixing of the competing populations. When the groups are nearly block-separated, the interaction effect re-emerges. The control scenarios for competing subpopulations show a Nash equilibrium in the infection load pay-off matrix when they are cooperating in a combined vaccination-confinement strategy. The obtained infection-load pay-off matrices for two competing subpopulations do show effects that are specific to the type of implemented vaccination and confinement here. In particular, competition for the limited vaccination capacity shows a diminished overall improvement in a block-separated subpopulation in comparison to a configuration with a homogeneously spread subpopulation.

A scalarization method for multi-objective optimization was used to integrate the objective of the minimization of the infection load with a penalty—or proxy cost—for deploying a control policy with a lower preference ranking in a subpopulation. The shifting of the Nash equilibrium over the compounded payoff matrix was observed for differing control policy preferences, and their intensities, in the two subpopulations. In particular, the intensity of the control policy rankings and the prioritization—or not—of the infection load reduction over policy ranking adherence, influence the proneness of the Nash equilibrium to shift. The variability of the Nash equilibrium was also shown to be higher in the homogeneous spreading of the subpopulations in comparison to the block spreading. With homogeneous spreading, an increased policy ranking intensity will move the Nash Equilibrium towards a competitive scenario that includes a more preferred strategy. This effect is more prominent when the policy preference ranking objective is on par with the objective of infection load reduction.

In our future work, a systematic exploration of cost factors (economic attrition and healthcare expenditure) due to confinement variations and vaccination methods is envisaged (multiple types, repeated administration). Furthermore, the extension of the epidemic SEIRSD model into a probabilistic epidemic diffusion model on social-contact networks will allow covering periodically resurgent diseases. Finally, instead of randomly generated configurations, more realistic distributions of contact ego-networks, and an improved allocation of individual infection and recovery rates can be implemented (according to age or medical preconditions, or GDP, prevailing in subpopulations). Moreover, the effects can be studied when the control scenarios and e.g. the intensities of the infectious exposures between nodes are modulated continuously over time.

Appendices

Appendix A. Formal implementation method for graph adjacency

The infection load of a SIR-epidemic on a graph depends on the structure of the social contact graph, epidemic infection and recovery rates of the population and spreading of the subpopulations, and specific implementation and parametrization of the control scenarios. The specific implementations of the social-contact graph features for the reported simulations are provided in this appendix. A sorted adjacency matrix is obtained from a random sampling of row-sorted and column-sorted random matrices. The randomized adjacency matrix is obtained by correlated row-column shuffling. The final probabilistic adjacency matrix is obtained by weighting the sorted and shuffled matrices with the skew parameter. Clustering and cliques formation occurs in the dense ordered diagonal zone, hence skew decreases clustering.

Appendix B. Preference payoff matrix design

The policy preference payoff matrix, $P_{\textit{PR}_{ij}}$, consists of the ranking weights $w_{i[j]}$ derived from the policy rankings of the subpopulations, $O_{0}$ and $O_{1}$, Sect. 4.3, according the multiplicative weighting scheme (Saaty, 1978; Zhang et al., 2004). The present algorithm transforms the rankings to weights in relation to the intensity, ${\mathscr {I}}$, of the ranking, and orders them with respect to the fixed order of controls, Eq. 8, in the policy ranking payoff matrix according $P_{\textit{PR}_{ij}} = [w_0(I_0)_i\,, w_1(I_1)_j]$, Eq. (15).

Appendix C. Multiplicative Weighting & Illustrative Example

Consider the objective rankings for control strategies of the j-th sub-population are given by:

$$\begin{aligned} O_j = \begin{bmatrix} O_{j,1},&O_{j,2},&O_{j,3},&O_{j,4} \end{bmatrix} = \begin{bmatrix} 1,&2,&3,&4\end{bmatrix} \end{aligned}$$

(A.1)

and the corresponding preference intensity is set to ‘5’, i.e., ${\mathcal {I}}_j=5$. For these preference specifications, the corresponding multiplicative preference weights can be determined by differencing and exponentialization according to Line 4–7, Algorithm 2:

$$\begin{aligned} \begin{bmatrix} \tau _{1,1} &{}\quad \tau _{1,2} &{}\quad \tau _{1,3} &{}\quad \tau _{1,4}\\ \tau _{2,1} &{}\quad \tau _{2,2} &{}\quad \tau _{2,3} &{}\quad \tau _{2,4}\\ \tau _{3,1} &{}\quad \tau _{3,2} &{}\quad \tau _{3,3} &{}\quad \tau _{3,4}\\ \tau _{4,1} &{}\quad \tau _{4,2} &{}\quad \tau _{4,3} &{}\quad \tau _{4,4}\\ \end{bmatrix} = \begin{bmatrix} 1 &{}\quad 5^\frac{1}{3} &{}\quad 5^\frac{2}{3} &{}\quad 5\\ 5^{-\frac{1}{3}} &{}\quad 1 &{}\quad 5^\frac{1}{3} &{}\quad 5^\frac{2}{3}\\ 5^{-\frac{2}{3}} &{}\quad 5^{-\frac{1}{3}} &{}\quad 1 &{}\quad 5^\frac{1}{3}\\ 5^{-1} &{}\quad 5^{-\frac{2}{3}} &{}\quad 5^{-\frac{1}{3}} &{}\quad 1 \end{bmatrix} \end{aligned}$$

Subsequently, the preference weights are determined by multiplication and power elevation according to Line 8, Algorithm 2:

$$\begin{aligned} \begin{bmatrix} w_1&w_2&w_3&w_4\end{bmatrix}&=\begin{bmatrix} 2.2361&1.3077&0.7647&0.4472 \end{bmatrix}\\ \text {which gives, }\ \ \ \ \ W&= \frac{\begin{bmatrix} w_1,&\dots ,&w_4\end{bmatrix}^T}{\sum w} = \begin{bmatrix} 0.4702&0.2750&0.1608&0.0940\end{bmatrix}. \end{aligned}$$

These weight vectors, $W_{group}$, are finally constituting the entries of the policy ranking payoff matrix, respectively for each subpopulation.