Abstract
Okasha, in Evolution and the Levels of Selection, convincingly argues that two rival statistical decompositions of covariance, namely contextual analysis and the neighbour approach, are better causal decompositions than the hierarchical Price approach. However, he claims that this result cannot be generalized in the special case of soft selection and argues that the Price approach represents in this case a better option. He provides several arguments to substantiate this claim. In this paper, I demonstrate that these arguments are flawed and argue that neither the Price equation nor the contextual and neighbour partitionings sensu Okasha are adequate causal decompositions in cases of soft selection. The Price partitioning is generally unable to detect cross-level by-products and this naturally also applies to soft selection. Both contextual and neighbour partitionings violate the fundamental principle of determinism that the same cause always produces the same effect. I argue that a fourth partitioning widely used in the contemporary social sciences, under the generic term of ‘hierarchical linear model’ and related to contextual analysis understood broadly, addresses the shortcomings of the three other partitionings and thus represents a better causal decomposition. I then defend this model against the argument that because it predicts that there is some organismal selection in some specific cases of segregation distortion then it should be rejected. I show that cases of segregation distortion that intuitively seem to contradict the conclusion drawn from the hierarchical linear model are in fact cases of multilevel selection 2 while the assessment of the different partitionings are restricted to multilevel selection 1.


Similar content being viewed by others
Notes
The two levels scenario will be the one I will use throughout the paper.
For simplicity discrete generations are assumed.
It is in fact the particle’s contextual character, but since a perfect mapping between the contextual and collective character exists, for simplicity, I will use “collective character” in the reminder of the paper in places where it should be “contextual character”.
Note that the term ‘effect’ is understood here in a metaphysical sense, not a causal one. It thus includes supervenience relations.
Note that Okasha (2006, 201) points out that in some case of emergent collective character it might be worth including these effects in the collective level character. For the purpose of this paper I will not consider those cases.
See Appendix for a formal definition of neighbourhood character.
Each of these two approaches has different advantages and disadvantages, but they are unimportant for the main purpose of this paper.
Mutatis mutandis, the same can be argued for neighbour partitioning, for there is a straightforward relation between contextual and neighbour partitionings (see Appendix).
Note that Laplacian determinism can be supposed in all the equations of this paper and it is also what has been supposed by Okasha throughout his book. I will follow suit.
Note that I am talking here about the same type of collective character which might be realized by different tokens as is the case in Fig. 1 with the collective characters of collectives 2 and 3 which are the same but realized in two different ways.
Note that these do not represent mutually exclusive situations: the overall difference could be attributed a combination of these three causes.
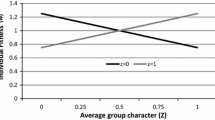
Note that other complex scenario of multilevel selection, some involving soft selection while others not, are expected to violate the fundamental principle of determinism in deterministic settings when modelised by contextual analysis. Therefore my demonstration is not intended to apply solely to soft selection cases, but these are the ones I take issue with in this paper.
As previously, everything said about contextual analysis can be transposed to neighbour partitioning (see Appendix). To classical contextual analysis, corresponds a classical form of neighbour partitioning.
Note that Gardner (2015a) develops a similar analysis in the context of the hierarchical form of the Price equation.
See also another case of segregation distortion at the same page, which can be treated in a similar way.
Effectively, as I pointed earlier, this is equivalent to a case of classical contextual analysis (Eq. 4).
Other cases would involve more complex models.
References
Bourrat P (2015a) Levels, time and fitness in evolutionary transitions in individuality. Philosophy & Theory in Biology 7. doi:10.3998/ptb.6959004.0007.001
Bourrat P (2015b) Levels of selection are artefacts of different fitness temporal measures. Ratio 28 (1):40–50. doi:10.1111/rati.12053
Boyd LH, Iversen GR (1979) Contextual analysis: concepts and statistical techniques. Wadsworth Publishing Company, Belmont
Damuth J, Heisler IL (1988) Alternative formulations of multilevel selection. Biol Philos 3(4):407–430
De Leeuw J, Meijer E (2008) Introduction to multilevel analysis. In: De Leeuw J, Meijer E (eds) Handbook of multilevel analysis. Springer, New York, pp 1–75
Falk R, Sarkar S (1992) Harmony from discord. Biol Philos 7(4):463–472
Frank SA (1998) Foundations of social evolution. Princeton University Press, Princeton
Frank SA (2012) Natural selection. IV. The Price equation. J Evol Biol 25(6):1002–1019
Gardner A (2015a) The genetical theory of multilevel selection. J Evol Biol 28(2):305–319
Gardner A (2015b) More on the genetical theory of multilevel selection. J Evol Biol 28(9):1747–1751
Goldstein H (2011) Multilevel statistical models, 4th edn. Wiley, Chichester
Goodnight CJ (2015) Multilevel selection theory and evidence: a critique of Gardner, 2015. J Evol Biol 28(9):1734–1746
Goodnight CJ, Schwartz JM, Stevens L (1992) Contextual analysis of models of group selection, soft selection, hard selection and the evolution of altruism. Am Nat 140(5):743–761
Heisler L, Damuth J (1987) A method for analyzing selection in hierarchically structured populations. Am Nat 130(4):582–602
Hox JJ (2010) Multilevel analysis: techniques and applications. Routledge, New York
Lande R, Arnold SJ (1983) The measurement of selection on correlated characters. Evolution 37(6):1210–1226
Lewontin RC (1970) The units of selection. Annu Rev Ecol Syst 1(1):1–18
Mitchell-Olds T, Shaw RG (1987) Regression analysis of natural selection: statistical inference and biological interpretation. Evolution 41(6):1149–1161
Nunney L (1985) Group selection, altruism, and structured-deme models. Am Nat 126(2):212–230
Okasha S (2004) Multilevel selection and the partitioning of covariance: a comparison of three approaches. Evolution 58(3):486–494
Okasha S (2005) Altruism, group selection and correlated interaction. Br J Philos Sci 56(4):703–725
Okasha S (2006) Evolution and the levels of selection. Oxford University Press, New York
Price GR (1970) Selection and covariance. Nature 227:520–521
Price GR (1972) Extension of covariance selection mathematics. Ann Hum Genet 35(4):485–490
Robertson A (1966) A mathematical model of the culling process in dairy cattle. Anim Prod 8(95):108
Sarkar S (1994) The selection of alleles and the additivity of variance. In: PSA: proceedings of the biennial meeting of the Philosophy of Science Association, pp 3–12
Sarkar S (1998) Genetics and reductionism. Cambridge University Press, Cambridge
Snijders TAB, Bosker RJ (1999) Multilevel analysis: an introduction to basic and advanced multilevel modeling. Sage, London
Sober E, Wilson DS (2011) Adaptation and natural selection revisited. J Evol Biol 24(2):462–468
Stevens L, Goodnight CJ, Kalisz S (1995) Multilevel selection in natural populations of impatiens capensis. Am Nat 145(4):513–526
Wade MJ (1985) Soft selection, hard selection, kin selection, and group selection. Am Nat 125(1):61–73
Wallace B (1975) Hard and soft selection revisited. Evolution 29(3):465–473
Williams GC (1966) Adaptation and natural selection: a critique of some current evolutionary thought. Princeton University Press, Princeton
Acknowledgments
I am thankful to Andy Gardner, Charles Goodnight, Samir Okasha and three anonymous reviewer for comments on earlier versions of the manuscript and Peter Godfrey-Smith for his advice on this topic. I am also grateful to Paul Griffiths for his support over the years. This research was supported under Australian Research Council’s Discovery Projects funding scheme (Projects DP150102875).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Okasha (2005, 718–719) provides a definition of \(\beta_{4}\) in terms of collective characters and particle characters by demonstrating that there is the simple relation following relation between \(\beta_{2}\) and \(\beta_{4}\). Given that neighbourhood character is defined as \(X_{jk} = \frac{{nZ_{k} - z_{jk} }}{n - 1}\), we can deduct that
where \(n\) is the number of particles in a collective.
Although Okasha does not provide a demonstration of it, it is also useful to express \(\beta_{3}\) in terms of collective and particle characters. In fact, this will allows us to highlight the difference between the direct effect of particle character on particle fitness, controlling for collective character and the direct effect of particle character on particle fitness, controlling for neighbourhood character. This also highlights the straightforward mathematical link between contextual and neighbour partitionings. This can be done as follows. Assuming \(e_{jk}\) is nil we have:
This expression can be rearranged as follows:
Because both the contextual and Okasha’s version of the neighbourhood regression models are models for particle fitness, we know that:
And thus it follows that:
This implies that:
and therefore that:
Recall that Okasha defines \(\beta_{3}\) as the partial regression coefficient of fitness on particle character, controlling for neighbourhood character. We can now express it verbally in terms of particle and collective characters. Following the definitions of \(\beta_{1}\), \(\beta_{2}\) and \(n\) provided in the main text, \(\beta_{3}\) is the sum of the partial regression coefficient of particle fitness on particle character, controlling for collective character and the partial regression coefficient of fitness on collective character, controlling for particle character, divided by the number of particles in the collective.
Rights and permissions
About this article
Cite this article
Bourrat, P. Generalizing Contextual Analysis. Acta Biotheor 64, 197–217 (2016). https://doi.org/10.1007/s10441-016-9280-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10441-016-9280-5