Global Stability of Reversible Enzymatic Metabolic Chains

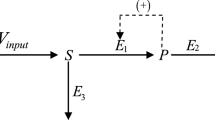
Abstract

We consider metabolic networks with reversible enzymatic reactions. The model is written as a system of ordinary differential equations, possibly with inputs and outputs. We prove the global stability of the equilibrium (if it exists), using techniques of monotone systems and compartmental matrices. We show that the equilibrium does not always exist. Finally, we consider a metabolic system coupled with a genetic network, and we study the dependence of the metabolic equilibrium (if it exists) with respect to concentrations of enzymes. We give some conclusions concerning the dynamical behavior of coupled genetic/metabolic systems.

Appendices

APPENDIX

1.1 Monotone Systems

Monotone systems form an important class of dynamical systems, and are particularly well adapted to mathematical models in biology (Sontag 2004), because they are defined by conditions related to the signs of Jacobian matrix. Such a sign for one element traduces the fact that some variable will contribute positively to the variation of some other variables, and this kind of qualitative dependence is very frequent in biological models. The reader may consult the reference (Smith 1995) for a review or an exhaustive presentation of the theory of monotone systems.

First we give some definitions. We are working with system

$$ \dot{x}=f(x) $$

(15)

in a domain X of n-dimensional space ${{\mathbb{R}}^n}$. In this paper ${X={\mathbb{R}}_{+}^{n}}.$

Partial order Let the positive cone K that satisfies the properties:

• $\alpha K\subset K$ for all ${\alpha \in{\mathbb{R}}_{+}}$

• $K + K \subset K$

• K ∩ (− K) = {0}

A partial order $\succeq$ in K is defined in the following way between two points of $X:\, x_1 \succeq x_2 \Leftrightarrow x_1 - x_2 \in K$ (in the following, we choose ${K={\mathbb{R}}^n_{+}}$, which is the classical usual positive cone).

Definition 1

Kamke Condition

f is of type K for all i, if $f_i(a)\succeq f_i(b)$ for all points a and b in X such that $a \succeq b$ and a _i  = b _i .

The following theorem is instrumental: it says that, if two initial conditions are ordered, then the solutions of (15) from these two initial conditions will remain ordered for all time t.

Theorem 1

Let f of type K and $x_0, x_1 \in X$. If $x_0 \succeq x_1$ and $\Upphi(t,x_i) \,\, (i=0,1)$ are defined, then $\Upphi(t,x_0) \succeq \Upphi(t,x_1)$ for all t.

See (Smith 1995, p. 32) for the proof. The Kamke condition is easier to check by looking at the signs of the elements of the Jacobian matrix of system (1).

Proposition 11

If f is differentiable, then Kamke condition implies

$$ \frac{\partial f_i}{\partial x_j}(x) \geq 0 \quad \forall i\neq j $$

(16)

Conversely, if $\frac{\partial f_i}{\partial x_j} (x)$ is continuous and satisfies (16) in X, and if the domain X is p-convex (i.e. for all x and y in X satisfying $x \succeq y$, the segment joining the two points is in X), then the Kamke condition is satisfied.

See (Smith 1995, p. 33) for a proof. System (1) is called a cooperative system. In summary, if the system is cooperative, then the flow is monotone, and preserves the partial order in ${{\mathbb{R}}^n}$. These systems have a strong tendency to converge to the set of their equilibria (Smith 1995, p. 57). It can be shown that almost any solution converges to the set of equilibria except a set of zero measure. In particular, there are no stable periodic solutions. For more precise theorems, see (Smith 1995).

1.2 Compartmental Systems

Let us now give a few reminders about compartmental systems (see Jacquez and Simon 1993). This kind of models describes the dynamics of n-compartments interconnected by links with fluxes of matter. The overall equation is written by making a global mass balance between inputs and outputs of each compartment. The definition of a compartmental matrix is the following:

Definition 2

Compartmental Matrix

The n × n matrix C is a compartmental matrix if it satisfies the following three properties (Jacquez and Simon 1993):

$$ C_{ii} \leq 0 \,\, i=1,\dots,n, $$

(17)

$$ C_{ij} \geq 0 \quad for \quad i\, \ne j,\,\, i, j=1,\dots,n, $$

(18)

$$ -C_{jj} \geq \sum_{i\ne j} C_{ij} \quad j=1,\dots,n, $$

(19)

Note that C _ij can in general depend on $x_k, \, k = 1\ldots n$ which are the concentrations in each compartment. A common case is when C _ij , flow from compartment j in the compartment i, depends only on x _j (thus on the concentration of the initial compartment). This is not the case in our systems. There are also some theorems on the stability of linear and nonlinear compartmental systems (see Jacquez and Simon 1993).

The following theorem (theorem 8 p. 56 in Jacquez and Simon 1993) gives global stability results.

Theorem 2

Let

$$ \dot{x}= f(x) $$

(20)

and the three conditions

• (S1)

  $$ \frac{\partial f_i}{\partial x_j}\geq 0 \quad for \,\, i \ne j,\quad\, i,j=1,\ldots.,n, $$

• (S2)

  $$ \sigma(x)=\sum_{i=1,\dots,n} \dot{x}_i $$

  is such that

  $$ \frac{\partial \sigma}{\partial x_i} < 0 \quad i=1,\ldots.,n $$

• (S3) It exists k > 0 such that σ(x) ≤ 0 when $\sum\nolimits_{i=1,\ldots,n} x_i=k$

If conditions (S1), (S2), (S3) are satisfied, then system (20) has a unique globally stable equilibrium.

The following property (Jacquez and Simon 1993, p. 54) is linked to monotonicity of the flow.

Proposition 12

If J(x) is a compartmental matrix ${\forall x\in {\mathbb{R}}^n_{+}}$, then all bounded trajectories converge toward an equilibrium in ${{\mathbb{R}}^n_{+}}$.

We recall (Jacquez and Simon 1993, p. 47) that a graph is said strongly connected if there is a directed path from any compartment to any other compartment; equivalently, the corresponding matrix is irreducible. Now the following theorem is for closed systems, meaning, in this case, that total concentration ∑x _i is conserved (∑ ⁿ _i=1 f _i (x) = 0).

Theorem 3

Property 5 in (Bastin and Guffens 2006)

Suppose system (20) is closed, and let M(x) = ∑ ⁿ _i=1 x _i the fixed total concentration.

If the Jacobian matrix of the system is irreducible (the system is strongly connected) and compartmental, then for any M ₀ > 0, hyperplane ${H=\{x \in {\mathbb{R}}^n_{+}: M(x)=M_0>0\}}$ is invariant and contains a unique globally stable equilibrium in H.

We recall some definitions and properties concerning output, see (Jacquez and Simon 1993, p. 47) and (Bastin and Guffens 2006).

Definition 3

Fully outflow connected network

A compartment x _i is outflow (output) connected if there is a path $x_i \rightarrow x_j \rightarrow\ldots\rightarrow x_l$ from x _i until a compartment x _l with an outflow. The network is fully outflow connected if all compartments are outflow connected.

The following proposition is in (Jacquez and Simon 1993, p. 52).

Proposition 13

Invertibility of a compartmental matrix

A compartmental matrix is regular if and only if the associated network is fully outflow connected.

Intuitively, it means that the system has no traps where the flows accumulate (see Jacquez and Simon 1993). We recall that in this case the matrix has eigenvalues with negative real parts (Jacquez and Simon 1993, p. 51), and the associated linear system is asymptotically stable.

Tikhonov Theorem

Consider the system

$$ \Upsigma^{\varepsilon} \left\{ \begin{array}{l} \frac{d x}{d t}=\varepsilon f(x,z,\varepsilon)\\ \frac{d z}{d t}= g(x,z,\varepsilon)\\ \end{array} \right. $$

(21)

If the following conditions are fulfilled

Assumption 1

z = ρ(x) is the solution of g(x, z, 0) = 0, function ρ is regular, and matrix $\frac{\partial g}{\partial z} (x,\rho(x),0)$ has eigenvalues with negative real part.

Assumption 2

Reduced system

$$ \Upsigma^{0} \left\{ \begin{array}{ll} \frac{d x}{d \tau}=f(x,\rho(x),0)\\ x_{(\tau=0)}=x_0 \\ \end{array} \right. $$

(22)

with $\tau = \varepsilon t$ has a unique solution x ₀(τ) for $\tau \in [0, T],\, 0<T<+\infty$

Then, for $\varepsilon$ small enough, the full system $(\Upsigma^{\varepsilon})$ has a unique solution $(x_{\varepsilon}(\tau),z_{\varepsilon}(\tau))$ for $\tau \in [0, T]$, if z ⁰ is in the basin of attraction of equilibrium ρ(x ⁰) of the rapid system

$$ \frac{d \xi}{d t}= g(x^0,\xi,0) $$

(23)

and for $\tau \in [a, T]$ (a > 0),

$$ lim_{\varepsilon \rightarrow 0^+} x_\varepsilon (\tau)=x_0 (\tau), lim_{\varepsilon \rightarrow 0^+} z_\varepsilon (\tau)=\rho(x_0 (\tau)) $$

The limits are uniform with respect to time. The theorem (and more details) is in (Khalil 2002, p. 434). Without further assumptions, the result is only valid for finite time T. Extensions are possible for infinite time, giving therefore asymptotic properties. For example, if the reduced system has an hyperbolic asymptotically stable equilibrium point $\bar{x}$, then, for $\varepsilon$ small enough, the full system also admits an hyperbolic stable equilibrium, closed to $\bar{x}$. The approximation is therefore valid for infinite time (see Khalil 2002, p. 439).