Prediction on nonlinear mechanical performance of random particulate composites by a statistical second-order reduced multiscale approach

Abstract

A novel statistical second-order reduced multiscale (SSRM) approach is established for nonlinear composite materials with random distribution of grains. For these composites considered in this work, the complex microstructure of grains, including their shape, orientation, size, spatial distribution, volume fraction and so on, results in changing of the macroscopic mechanical properties. The first- and second-order unit cell functions based on two-scale asymptotic expressions are constructed at first. Then, the expected homogenized parameters are defined, and the nonlinear homogenization equation on global structure is established, successively. Further, an effective reduced model format for analyzing second-order nonlinear unit cell problem with less computation cost is introduced in detail. Finally, some numerical examples for the materials with varying distribution models are evaluated and compared with the data by theoretical models and experimental results. These examples illustrate that the proposed SSRM approaches are effective for predicting the macroscopic properties of the random composite materials and supply a potential application in actual engineering computation.

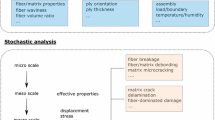
Graphic Abstract

Appendices

Appendix A

Inserting Eqs. (3)–(5) into Eq. (1), and considering the coefficients of the same power for $\xi$ yields

$$\begin{gathered} - \frac{\partial }{{\partial x_{j} }}\left\{ {L_{ijkl} (\frac{{\mathbf{x}}}{\xi },\omega )\varepsilon_{kl}^{\xi } \left[ {{\mathbf{u}}^{\xi } ({\mathbf{x}},\omega )} \right]} \right\}{ + }\frac{\partial }{{\partial x_{j} }}\left[ {L_{ijkl} (\frac{{\mathbf{x}}}{\xi },\omega )\mu_{kl}^{\xi } ({\mathbf{x}},\omega )} \right] \hfill \\ = - \xi^{ - 1} \frac{{\partial L_{ijkl} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{j} }}\frac{1}{2}(\frac{{\partial u_{k}^{0} }}{{\partial x_{l} }} + \frac{{\partial u_{l}^{0} }}{{\partial x_{k} }}) - \xi^{ - 1} \frac{\partial }{{\partial y_{j} }}\left\{ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\frac{1}{2}\left[ {\frac{{\partial H_{k}^{{\alpha_{1} m}} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{l} }}} \right.} \right. \hfill \\ + \left. {\left. {\frac{{\partial H_{l}^{{\alpha_{1} m}} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{k} }}} \right]} \right\}\frac{{\partial u_{m}^{0} }}{{\partial x_{{\alpha_{1} }} }} - \xi^{ - 1} \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {h_{{k,y_{l} }}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{mn}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} ){\text{d}} \tilde{\Theta }} \right] \hfill \\ + \xi^{ - 1} \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijmn} ({\mathbf{y}},\omega^{s} )\mu_{mn}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} )} \right] - \xi^{0} \left\{ {\frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\frac{1}{2}(\frac{{\partial \Phi_{km}^{{\alpha_{1} \alpha_{2} }} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{l} }}} \right.} \right. \hfill \\ + \left. {\frac{{\partial \Phi_{lm}^{{\alpha_{1} \alpha_{2} }} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{k} }}} \right] + \frac{\partial }{{\partial y_{j} }}\left[ {L_{{ijk\alpha_{2} }} ({\mathbf{y}},\omega^{s} )H_{k}^{{\alpha_{1} m}} ({\mathbf{y}},\omega^{s} )} \right] + L_{{i\alpha_{1} m\alpha_{2} }} ({\mathbf{y}},\omega^{s} ) \hfill \\ + \left. {L_{{i\alpha_{1} kj}} ({\mathbf{y}},\omega^{s} )\frac{{\partial H_{k}^{{\alpha_{2} m}} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{j} }}} \right\}\frac{{\partial^{2} u_{m}^{0} }}{{\partial x_{{\alpha_{1} }} \partial x_{{\alpha_{2} }} }} \hfill \\ - \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {h_{k}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{{mn,x_{l} }}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} ){\text{d}} \tilde{\Theta }} \right] \hfill \\ - L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {h_{{k,y_{l} }}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{{mn,x_{j} }}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} ){\text{d}} \tilde{\Theta } + L_{ijkl} ({\mathbf{y}},\omega^{s} )\mu_{{kl,x_{j} }}^{f} ({\mathbf{x}},{\mathbf{y}},\omega^{s} ) \hfill \\ - \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {\phi_{{kp,y_{l} }}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{{mn,x_{p} }}^{f} {\text{d}} \tilde{\Theta }} \right] + O(\xi ) = f_{i} ({\mathbf{x}}). \hfill \\ \end{gathered}$$

(A.1)

Next, comparing the coefficient of $\xi^{0}$ on both sides of (A.1) and using the homogenization Eq. (13) yield to

$$\begin{gathered} - \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\frac{{\partial \Phi_{kp}^{mn} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{l} }}} \right]\frac{{\partial \varepsilon_{mn}^{c} ({\mathbf{x}})}}{{\partial x_{p} }} \hfill \\ = - \frac{\partial }{{\partial x_{j} }}\left[ {\overline{L}_{ijkl} \frac{{\partial u_{k}^{0} ({\mathbf{x}})}}{{\partial x_{l} }}} \right] + \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )H_{k}^{mn} ({\mathbf{y}},\omega^{s} )\frac{{\partial \varepsilon_{mn}^{c} ({\mathbf{x}})}}{{\partial x_{l} }}} \right] \hfill \\ + \frac{\partial }{{\partial x_{j} }}\left\{ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\left[ {\frac{{\partial u_{k}^{0} ({\mathbf{x}})}}{{\partial x_{l} }} + \frac{{\partial H_{k}^{mn} ({\mathbf{y}},\omega^{s} )}}{{\partial y_{l} }}\varepsilon_{mn}^{c} ({\mathbf{x}})} \right]} \right\} \hfill \\ - \frac{{\partial \overline{A}_{ij} ({\mathbf{x}})}}{{\partial x_{j} }} + \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {h_{k}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{{mn,x_{l} }}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} ){\text{d}} \tilde{\Theta }} \right] \hfill \\ + L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {h_{{k,y_{l} }}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{{mn,x_{j} }}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} ){\text{d}} \tilde{\Theta } \hfill \\ + \frac{\partial }{{\partial y_{j} }}\left[ {L_{ijkl} ({\mathbf{y}},\omega^{s} )\int_{\Theta } {\phi_{{kp,y_{l} }}^{mn} ({\mathbf{y}},{\tilde{\mathbf{y}}},\omega^{s} )} \mu_{{mn,x_{p} }}^{f} ({\mathbf{x}},{\tilde{\mathbf{y}}},\omega^{s} ){\text{d}} \tilde{\Theta }} \right] \\ - L_{ijkl} ({\mathbf{y}},\omega^{s} )\mu_{{kl,x_{j} }}^{f} ({\mathbf{x}},{\mathbf{y}},\omega^{s} ) \hfill \\ \end{gathered}$$

(A.2)

Appendix B

In this work, continuum damage mechanic with isotropic damage law is applied to model constitutive behaviors of microconstituents. By this method, the constitutive relations are described by

$$\sigma_{ij} = (1 - \omega_{{\text{ph}}} )L_{ijkl} \varepsilon_{kl} ,$$

(B.1)

where $\omega_{ph} \in [0,1]$ is a damage state variable. Therefore, the partitioned eigenstrains are introduced by

$$\mu_{ij}^{(\alpha )} = \omega_{{\text{ph}}}^{(\alpha )} \varepsilon_{ij}^{(\alpha )} .$$

(B.2)

The damage state variables $\omega_{{\text{ph}}}^{(\alpha )}$ are the piecewise-continuous functions of damage equivalent strains $\kappa_{{\text{ph}}}^{(\alpha )}$. The evolutions of phase damage are introduced by

$$\omega_{{\text{ph}}}^{(\alpha )} = \left\{ \begin{gathered} 0,\;\;\;\;\;\;\;\;\;\kappa_{{\text{ph}}}^{(\alpha )} \le {}^{1}\kappa_{{\text{ph}}}^{(\alpha )} , \hfill \\ \Phi (\kappa_{{\text{ph}}}^{(\alpha )} ),\;\;\;\;{}^{1}\kappa_{{\text{ph}}}^{(\alpha )} < \kappa_{{\text{ph}}}^{(\alpha )} \le {}^{2}\kappa_{{\text{ph}}}^{(\alpha )} , \hfill \\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\kappa_{{\text{ph}}}^{(\alpha )} > {}^{2}\kappa_{{\text{ph}}}^{(\alpha )} ,\; \hfill \\ \end{gathered} \right.$$

(B.3)

where ${}^{1}\kappa_{{\text{ph}}}^{(\alpha )}$ and ${}^{2}\kappa_{{\text{ph}}}^{(\alpha )}$ are the parameters about the initial and fully damaged state, respectively. Also, we can refer to Ref. [63] for various $\Phi (\kappa_{{\text{ph}}}^{(\alpha )} )$. The damage equivalent strain $\kappa_{{\text{ph}}}^{(\alpha )}$ are supposed to be a function of the principal strain

$$\kappa_{{\text{ph}}}^{(\alpha )} (t) = \max \left[ {\sqrt {\sum\limits_{I = 1}^{3} {\langle \varepsilon_{I}^{(\alpha )} (\tau )\rangle^{2} } } ,\;\tau < t} \right],$$

(B.4)

where

$$\langle x\rangle = \left\{ \begin{gathered} x,\;\;\;\;\;x \ge 0, \hfill \\ Cx,\;\;\;x < 0, \hfill \\ \end{gathered} \right.$$

(B.5)

and C is the compression factor. ${}^{1}\kappa_{{\text{ph}}}^{(\alpha )}$ is determined by material strength S and stiffness E by

$${}^{1}\kappa_{{\text{ph}}}^{(\alpha )} = \frac{S}{E}.$$

(B.6)

According to the selection of damage evolution functions, ${}^{2}\kappa_{{\text{ph}}}^{(\alpha )}$ can be expressed in accordance with physical-based material parameters (E, S and G-the strain energies).