1 Introduction

Dispersion in microchannels is now an important consideration in the design of microelectromechanical systems, such as for drug delivery, component sensing, and microscale mixing. For their many applications in biomedical diagnosis and analysis, such as clinical detection, DNA hybridizations, and electrophoretic separations, lab-on-a-chip is an emerging technology drawing much attention nowadays. As it is important to effectively achieve mixing or separation in these microscale devices, dispersion mechanisms have been increasingly investigated under flow conditions that are specific to microfluidics. Compared to mechanical methods, the electrokinetic method viz. electroosmosis (EO), utilizing the electric double layer (EDL) effect to mobilize fluid, is now more acceptable for microfluidic devices as it offers the ability to control and drive the fluid by external means with no moving parts. The presence of an applied electric field, together with the EDL formed at the contact interface of an electrolyte and a solid surface, gives rise to electrokinetic phenomena, which in recent years have been extensively studied in the context of microfluidics and nanofluidics.

EDLs are formed as a result of interaction of an ionized solution with solid surfaces which possess electrostatic charges. The counter-ions in the liquid are attracted and the co-ions are repelled by the solid surfaces. The counter-ions thus cluster near the interface, forming the Stern layer. The characteristic electric potential of the Stern layer is known as the zeta potential denoted by ζ. Beyond the Stern layer, counter-ions are relatively free to move forming a diffuse layer. The EDL is the union of the Stern and diffuse layers, which shield the bulk of the electrolyte from the surface charge. The thickness of the EDL is represented by the Debye length, which is a scale of the distance from the charged solid interface to a point where the electrokinetic potential energy is equal to the thermal energy. When an external electric field is applied parallel to the solid surface, the co-ions and counter-ions will be attracted toward the anode and cathode, respectively, and by virtue of the viscous momentum transfer, adjacent fluids will be dragged and accelerated by the migrating ions. This phenomenon is called EO, and the resulting flow is called electroosmotic flow (EOF).

Dispersion in pressure-driven steady and oscillatory flows has been studied extensively, since the study of Aris (1956, 1960) who obtained the dispersion coefficient of a passive solute using the method of moments. The study was pioneered by Taylor (1953) who studied the “enhanced diffusion” of a solute in laminar flow through a circular tube, relative to a plane moving with the mean speed of the flow. The basic mechanism that contributes to the enhanced diffusion, now known as Taylor dispersion, is molecular diffusion occurring across lateral concentration gradients created by a nonuniform velocity field. Therefore, a sharper velocity gradient across the channel section can result in a greater dispersion effect. Recent interest in micro- and nano-fluidic applications has seen a dramatic increase of studies directed at the analysis of EOF and associated dispersion phenomena, applied as a means to control fluid transport, mixing, or separation.

Compared with transport in pressure-driven (Poiseuille) flow, EOF under the condition of a thin EDL may generate much weaker hydrodynamic dispersion. This is due to the fact that when the EDL is thin, the EOF is nearly a plug flow, which, in the absence of any shear, produces negligible dispersion.

However, under other conditions, dispersion in EOF may not be small. At sufficiently low electrolyte concentrations (lower than 10−3 M) such that the EDL is not thin, and under a strong applied electric field (on the order 100 V/mm), electroosmotic dispersion can become significant compared with molecular diffusion. In analytical studies involving separations, or simply detection of solutes, hydrodynamic dispersion may negatively influence the performance of the microfluidic device, thus reducing the quality of the measurement or the separation efficiency. In other cases involving chemical reactions, dispersion is, on the contrary, desirable as it can enhance mixing. Dispersion is indeed a function of many parameters; it can be small under certain conditions, but can be large under some other conditions. It is the aim of this study to look into ways to adjust dispersion in EOF. We specifically examine how dispersion can be affected by parameters in an EOF generated by oscillatory wall potentials interacting with an oscillatory electric field.

A number of studies on dispersion in micro- and nano-scale have been carried out recently. Some of them addressed pressure-driven flow, whereas in some studies electrically driven flow and combined pressure-electrically-driven flow were considered. Assuming low electric potentials at the wall/solution interface, Datta (1990), McEldoon and Datta (1992), and Griffiths and Nilson (1999) evaluated the electroosmotic dispersion coefficient for the circular and plane parallel channels. For higher wall potentials, the electroosmotic dispersion was addressed by Andreev and Lisin (1992, 1993), Gas et al. (1995), Griffiths and Nilson (2000), and Zholkovskij et al. (2003). Zholkovskij et al. (2003) analyzed the dispersion of a nonelectrolyte solute due to the EOF in a long straight microchannel using a thin double-layer approximation. Hydrodynamic dispersion due to combined pressure-driven and EOF through microchannels was addressed by Zholkovskij and Masliyah (2004). Dutta (2007) analyzed the electroosmotic transport of neutral samples through rectangular channels having a small zeta potential at the walls. A perturbative approach was used by Datta and Ghosal (2008) to analyze Taylor dispersion under non-ideal electroosmotic conditions in microfluidic systems. The flow-induced streaming potential was found by Xuan (2008) to significantly affect the solute transport and separation in nanochannel chromatography. Electrokinetic transport of charged samples through rectangular channels bearing small zeta potentials was analyzed by Dutta (2008). The broadening of a neutral solute band in electrically driven flow with longitudinally varying zeta potential was explored by Zholkovskij et al. (2010). Recently, Ng (2011) investigated the effect of wall slippage on hydrodynamic dispersion for some pressure-driven flows.

Dispersion in alternating current (AC) electrokinetic systems has also received attention for its relevance in the separation of species of colloids, or the trapping of particles in designated regions in microdevices. Time periodic EOF is also known as AC EO, and is driven by an alternating electric field which has potential applications in biotechnology and separation science. Huang and Lai (2006) have presented an analytical study of the enhanced mass transfer in an oscillatory EOF, within a parallel-plate microchannel configuration. Mass transfer in time periodic EOF through charged micro/nanochannel was discussed by Bhattacharyya and Nayak (2008). Ramon et al. (2011) studied solute dispersion subjected to boundary mass exchange in oscillatory EOF.

Kuo et al. (2008) proposed a mechanism by which a steady directional EOF can be produced by the nonlinear interaction between oscillatory wall potentials and oscillatory axial electric fields. For a two-dimensional plane channel, where time-periodic surface charge potentials are induced on the two walls, these authors showed that the flow velocity depends not on the external driving frequency, but on the phase difference between the electric field and the wall potentials. They further explained the driving mechanism of a steady mean flow due to this kind of nonlinear interaction, and pointed out the interrelationship between the AC EO and the static EO configurations. It is remarkable that the direction of the flow can be reversed by adjusting the phase of the wall potentials.

The mechanism of producing directional EOF as proposed by Kuo et al. (2008) can find potential applications in chromatography, particle sorting, separation, and so on. However, the mass transport in such a directional EOF is yet to be understood as a function of the driving forces. In view of this, this study aims to develop theoretical relations for solute transport in an oscillatory EO flow field generated by the nonlinear interaction between an oscillatory electric field and oscillatory wall potentials. The electric field and the two wall potentials are assumed to have the same frequency, but each wall potential can have a distinct phase lag with the electric field. The study of Kuo et al. (2008) is generalized and extended to this study of mass dispersion. The results of Kuo et al. (2008) may be recovered as a particular case of our flow in case of synchronized wall potentials (i.e., equal phases of the two wall potentials). The main objective here is to examine the effect of the EDL thickness (Debye length), oscillation parameters, and phases of the wall potentials on the EO velocity and hence the dispersion coefficient. The mathematical technique of homogenization is applied for the deduction of the effective mass transport equations. The dispersion coefficients are obtained as explicit functions of the above-mentioned controlling parameters.

The article is organized as follows. In the following section, the mathematical formulation of the problem is presented. Velocity distributions for electroosmotically driven flows are derived in Sect. 3. Concentration distribution of the solute is then discussed in Sect. 4, which is followed by an asymptotic analysis in Sect. 5. Finally, discussions and results are presented in Sect. 6.

2 Problem formulation

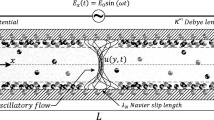
As shown in Fig. 1, we consider a two-dimensional parallel-plate microchannel of height 2h, which is filled with a liquid (the solvent) of aqueous nature. A Cartesian coordinate system is used here with the x-axis along the flow and the y-axis perpendicular to the flow. The boundaries are situated at y = ±h. EDLs are thus established at the two boundaries when the carrier liquid is brought into contact with the channel walls. A neutral species of concentration C(x, y, t), where t is time, is assumed to be carried with the fluid. An oscillatory axial electric field E is then imposed on the system; simultaneously AC voltages, having the same frequency but unequal phase lags with the oscillatory channel electric field, are applied on the two walls. As a result, a periodically oscillatory flow is generated due to the nonlinear interaction of the three oscillatory fields (Kuo et al. 2008). This study aims at investigating the effect on the mass dispersion due to convection of such an oscillatory EOF.

Fig. 1
figure 1

Schematic diagram of the system considered

Full size image

The fluid is assumed to be an isothermal, Newtonian, and incompressible continuum. For the present planar unsteady flow caused solely by electroosmotic mechanism, the fluid velocity is governed by the momentum equation

$$ \rho \frac{\partial u}{\partial t} = \mu \frac{\partial^2 u}{\partial {y}^2}+\rho_{\rm e} E, $$
(1)

where u is the fluid velocity along the x-direction, ρ and μ are the fluid density and viscosity, respectively, E is the applied electric field, and ρe is the electric charge density.

Equation 1 is subjected to no-slip boundary conditions at the walls. Here, the fluid viscosity is assumed to be independent of the local electric field strength. The first term on the R.H.S. of Eq. 1 is the viscous forcing term, while the last term, i.e., ρe E, represents the electrokinetic body force (Lorenz force) under the shielding effect of the EDL formed next to the surface (Levich 1962). This is the main driving force to generate the EOF.

In general, the electroosmotic body force term can exhibit various forms depending on the externally applied electric field. In this article, we consider sinusoidally driven, time-periodic pure EOFs in the absence of pressure gradients. The externally applied oscillatory electric field E directed along the x-axis is of the form

$$ E=E_0 \,\hbox{Re}(e^{i\omega t}) $$
(2)

with a constant amplitude E 0 and an excitation angular frequency ω. This external electric field interacts with the EDL and creates the electrokinetic body force on the bulk fluid.

When the solvent is a 1:1 symmetric electrolyte, the Boltzmann distribution of the charge density gives

$$ \rho_{\rm e}=-2 e z c_0 \, \sinh\left(\frac{ze\psi}{RT}\right), $$
(3)

where ψ is the electrokinetic potential, c 0 is the ion concentration far from the charged walls, z is the valence of the co- and counter-ions in the carrier liquid, e is the electron charge, R is the Boltzmann constant, and T is the absolute temperature. To apply the static Boltzmann distribution, we assume that the transience of the development of the EDLs is of a much shorter time scale than the time variations of the applied electric fields. Therefore, this theory is subjected to an upper frequency limit, which will be discussed in Sect. 4.

The charge potential ψ can be described by the following Poisson equation, giving the net excess charge density at a specific distance from the surface:

$$ \frac{{\text {d}}^2 \psi}{{\text {d}} y^2}=-\frac{\rho_{\rm e}}{\varepsilon}, $$
(4)

where ɛ is the permittivity of the liquid medium.

Combination of Eqs. 3 and 4 gives rise to the Poisson–Boltzmann equation, which describes how the electrostatic potential varies in space due to a distribution of charges:

$$ \frac{{\text {d}}^2 \psi}{{\text {d}} y^2}=\frac{2 e z c_0}{\varepsilon} \sinh \left(\frac{ze\psi}{RT}\right). $$
(5)

If the electric potential is sufficiently small, typically when ψ ≤ ψ0 ≈ 25mV, the Debye–Hückel approximation can be applied to Eq. 5 resulting in the following linear equation:

$$ \frac{{\text {d}}^2 \psi}{{\text {d}} y^2}=\frac{2e^2z^2c_0}{\varepsilon R T}\psi=\frac{\psi}{\Uplambda^2}, $$
(6)

where \(\Uplambda=(\varepsilon R T/2e^2z^2c_0)^{1/2}\) is the characteristic EDL thickness or the Debye length.

Thus, we have

$$ \frac{{\text {d}}^2 \psi}{{\text {d}} y^2}=k^2\psi, $$
(7)

where \(k=\Uplambda^{-1}\) is the reciprocal of the Debye length, also called the Debye–Hückel parameter. A larger value of k thus corresponds to a thinner double layer, whereas for a thicker double layer k is smaller.

The solution to Eq. 7 near a charged plate of potential ζ may be written as ψ = ζexp(−ky), where y is distance normal to the plate. Thus, the potential due to the charged plate is shielded by the free charges in solution and the effect of the charge penetrates a distance of the order of the Debye length \(\Uplambda,\) which gives a physical meaning to this very important quantity. The Debye length gives an estimate of the length scale over which an electrostatic perturbation (such as a charged surface) is shielded by rearrangement of ions.

The boundary conditions for Eq. 7 are prescribed by the wall potentials ψwall. In this study, AC voltages having unequal phase lags with the oscillatory axial electric field are applied on the two boundaries. The wall potential ψwall is of the form:

$$ \psi_{\rm wall}=\left\{ \begin{array}{ll} \psi_{\rm AC} \,\hbox{Re}[e^{i(\omega t +\beta)}]+\psi_{\rm DC}\quad\hbox{on}\quad y=h\\ \psi_{\rm AC} \,\hbox{Re}[e^{i(\omega t +\gamma)}]+\psi_{\rm DC}\quad\hbox{on}\quad y=-h \end{array}\right. $$
(8)

Here, ψAC is the amplitude of the applied AC potentials on the two walls, and β and \(\gamma\) are the phases of these potentials on the upper and the lower walls, respectively. The phase difference between the two wall potentials is thus \(\beta-\gamma.\) The potentials also contain a static base component ψDC. There are no specific assumptions on the orders of magnitude of ψAC and ψDC relative to each other, but to satisfy the linearization assumption, their maximum total values need to be small. Our flow model is based on the same theoretical arguments as those in Kuo et al. (2008).

Equation 7 along with the boundary conditions given by Eq. 8 yields the following solution

$$ \begin{aligned} \psi \;=\; &\psi_0\frac{\cosh(k y)}{2\cosh(k h )}\left\{\hat{\psi}_{\rm AC} \,\hbox{Re}\,\left[e^{i(\omega t+\beta)}\right]+\hat{\psi}_{\rm AC} \, \hbox{Re}\,\left[e^{i(\omega t+\gamma)}\right]+2\hat{\psi}_{\rm DC} \right\}\\ &+\psi_0\frac{\sinh(k y)}{2\sinh(k h )}\left\{ \hat{\psi}_{\rm AC} \, \hbox{Re}\,\left[e^{i(\omega t+\beta)}\right]-\hat{\psi}_{\rm AC} \, \hbox{Re}\,\left[e^{i(\omega t+\gamma)}\right]\right\} \end{aligned}, $$
(9)

where the dimensionless quantities (distinguished by a caret) used are

$$ (\hat{\psi}_{\rm AC}, \hat{\psi}_{\rm DC})=(\psi_{\rm AC}, \psi_{\rm DC})/\psi_0, $$

and ψ0 is a characteristic wall potential.

Using Eqs. 2, 4, and 7, Eq. 1 can be written as follows:

$$ \frac{1}{\nu}\frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial y^2}+k^2 U_{\rm HS} \frac{\psi}{\psi_0} \frac{E}{E_0}, $$
(10)

where U HS = −ε E 0 ψ0/μ is the Helmholtz–Smoluchowski velocity.

Now from Eqs. 2 and 9, we have the electrokinetic force be given by

$$ \begin{aligned} \frac{\psi}{\psi_0} \frac{E}{E_0} = &\frac{\hat{\psi}_{\rm AC}}{4}\left\{[\cos(\beta)+\cos(\gamma)] \frac{\cosh(ky)}{\cosh(kh)}+[\cos(\beta)-\cos(\gamma)]\frac{\sinh(ky)} {\sinh(kh)} \right\} \\ &+\hat{\psi}_{\rm DC}\frac{\cosh(ky)}{\cosh(kh)}\hbox{Re}(e^{i\omega t})+\left[\frac{\hat{\psi}_{\rm AC}}{4}\left(\frac{\cosh(ky)}{\cosh(kh)} +\frac{\sinh(ky)}{\sinh(kh)}\right)\right]\hbox{Re}[e^{i(2\omega t+\beta)}]\\ &+\left[\frac{\hat{\psi}_{\rm AC}}{4} \left(\frac{\cosh(ky)}{\cosh(kh)}-\frac{\sinh(ky)} {\sinh(kh)}\right)\right]\hbox{Re}[e^{i(2\omega t+\gamma)}], \end{aligned} $$
(11)

which comprises one steady component and three time-harmonic components. The steady component results from the non-linear interaction of the channel electric field with the oscillatory components of the wall potentials. This forcing drives a steady directional flow in the channel. The first-harmonic component containing e iωt is the result of interaction of the channel electric field with the steady components of the two wall potentials, while the higher-harmonic components containing e i(2ω t+β) and \(e^{i(2\omega t+\gamma)}\) are the other results of the channel electric field interacting with the oscillatory components of the upper and lower wall potentials, respectively. These three unsteady forcings generate oscillatory flows of the same frequency, all with a zero time-mean. Let us derive the velocity components in the following section.

3 Flow field

Equations 10 and 11 suggest a velocity profile of the form:

$$ u(y, t)=u_0(y)+\hbox{Re}[u_1(y)e^{i\omega t}]+\hbox{Re}[u_2(y)e^{i(2\omega t+\beta)}]+\hbox{Re}[u_3(y)e^{i(2\omega t+\gamma)}]. $$
(12)

The no-slip conditions at the channel walls u(±h, t) = 0 ensure that u j (±h, t) = 0, (j = 0, 1, 2, 3).

When Eqs. 11 and 12 are used in Eq. 10, the resultant solutions are found as follows:

$$ \begin{aligned} u_0(y) = &U_{\rm HS}\frac{\hat{\psi}_{\rm AC}}{4}\left\{[\cos(\beta)+\cos(\gamma)] \left[1-\frac{\cosh(ky)}{\cosh(kh)}\right]\right.\\ &+\left.[\cos(\beta)-\cos(\gamma)]\left[\frac{y}{h}- \frac{\sinh(ky)}{\sinh(k h)}\right]\right\}, \end{aligned} $$
(13)
$$ u_1(y)=U_{\rm HS}\hat{\psi}_{\rm DC}\frac{k^2}{k^2-\lambda^2} \left[\frac{\cosh(\lambda y)}{\cosh(\lambda h)}-\frac{\cosh(ky)}{\cosh(kh)}\right], $$
(14)
$$ \begin{aligned} u_2(y)&=U_{\rm HS}\frac{\hat{\psi}_{\rm AC}}{4}\frac{k^2} {k^2-2\lambda^2}\left[\left(\frac{\cosh(\sqrt{2}\lambda y)}{\cosh(\sqrt{2}\lambda h)}-\frac{\cosh(ky)}{\cosh(kh)}\right)\right.\\ &+\left.\left(\frac{\sinh(\sqrt{2}\lambda y)}{\sinh(\sqrt{2}\lambda h)}-\frac{\sinh(ky)}{\sinh(kh)}\right)\right],\\ \end{aligned} $$
(15)
$$ \begin{aligned} u_3(y)&=U_{\rm HS}\frac{\hat{\psi}_{\rm AC}}{4}\frac{k^2}{k^2-2\lambda^2} \left[\left(\frac{\cosh(\sqrt{2}\lambda y)}{\cosh(\sqrt{2}\lambda h)}-\frac{\cosh(ky)}{\cosh(kh)}\right)\right.\\ &-\left.\left(\frac{\sinh(\sqrt{2}\lambda y)}{\sinh(\sqrt{2}\lambda h)}-\frac{\sinh(ky)}{\sinh(kh)}\right)\right]. \end{aligned} $$
(16)

Here, λ = (iω/ν)1/2 = (1 + i)/δ, where δ = (2ν/ω)1/2 is the thickness of the Stokes boundary layer resulting from the oscillation of the flow. Note that the Stokes boundary layer is thinner for faster oscillation, and vice versa. The ratio δ/h is identified as an oscillation parameter.

In Eqs. 13–16, the terms containing ky as the argument of the hyperbolic functions are the particular solutions, while other terms are the added homogeneous solutions to satisfy the no-slip boundary conditions. Here, u 0 is the steady component which depends on the AC component \(\hat{\psi}_{\rm AC},\) the phase lags β and \(\gamma\) and the Debye–Hückel parameter k. The other three components (u 1, u 2, and u 3) are the complex amplitudes of the time-oscillatory components, which have strong dependence on the frequency parameter λ. The only velocity component that depends on the static base part \(\hat{\psi}_{\rm DC}\) of the wall potentials is u 1, which is a first-harmonic component. This component is derived from the nonlinear interaction of the oscillatory channel electric field with the steady component of the wall potentials. Driving forces of the velocity components u 2 and u 3, which are second harmonics, result from the interaction between the channel electric field and the oscillatory components of the upper and lower wall potentials, respectively.

The following properties regarding the velocity components are noteworthy. First, the steady component u 0 becomes an even or odd function of y when \(\cos(\beta)-\cos(\gamma)=0\) or \(\cos(\beta)+\cos(\gamma)=0,\) respectively. Second, in the particular case when \(\cos(\beta)=\cos(\gamma)=0\) or \(\beta=\gamma=\pi/2, u_0\) is identically zero. This is the case when the time oscillation of the electric field is orthogonal to that of the wall potentials, resulting in a zero net interaction between the two forcings. Third, when u 0 is an even function of y (i.e., \(\cos(\beta)-\cos(\gamma)=0\)), the steady flow is the maximum positive when \(\beta=\gamma=0\) (i.e., wall potentials synchronized with the electric field), and is the maximum negative when \(\beta=\gamma=\pi.\) The velocity gradient is always zero at the center of the channel. This is the case corresponding to strong convection but possibly weak dispersion. Fourth, when u 0 is an odd function of y (i.e., \(\cos(\beta)+\cos(\gamma)=0\)), the net steady flow is always zero as the forward and backward parts of the flow exactly balance each other. The velocity gradient at the center of the channel is the steepest when the peak u 0 (of either the forward or the backward flows) attains the largest magnitude, which happens when one phase is zero and the other phase is π. This is the case corresponding to zero convection but possibly the strongest dispersion. Fifth, the first-harmonic component u 1 is always an even function of y. Sixth, the second-harmonic components u 2 and u 3 are not independent but are related to each other by u 2(y) = u 3(− y). For in-phase wall potentials, \(\beta=\gamma,\) these two components can be merged, and the sum of the two amplitudes, u 2 + u 3, is an even function of y.

The model of Kuo et al. (2008) can be recovered by letting equal phases for the wall potentials, \(\beta=\gamma.\) Under this condition, the steady velocity component u 0 reduces to

$$ u_0(y)=U_{\rm HS}\frac{\hat{\psi}_{\rm AC}}{2}\cos(\beta) \left(1-\frac{\cosh(ky)}{\cosh(k h)}\right). $$

The component u 1 as given by Eq. 14 remains unchanged as it corresponds to the steady parts of the wall potentials, but u 2 and u 3 will then be merged into a single velocity component to produce

$$ u_2(y)+u_3(y)=U_{\rm HS}\frac{\hat{\psi}_{\rm AC}}{2} \frac{k^2}{k^2-2\lambda^2}\left(\frac{\cosh(\sqrt{2}\lambda y)}{\cosh(\sqrt{2}\lambda h)}-\frac{\cosh(ky)}{\cosh(kh)}\right). $$
(17)

Above all, if the wall potentials are completely steady (ψAC = 0, ψDC ≠ 0) and electric potential is also time independent (i.e., λ → 0), then the only non-vanishing velocity component u 1 becomes

$$ \lim_{\lambda \to 0} u_1(y)=U_{\rm HS}\hat{\psi}_{\rm DC}\left(1-\frac{\cosh(ky)}{\cosh(kh)}\right), $$

which is the well-known velocity profile for steady EOF in a two-dimensional channel. This shows the interrelationship between AC EOF and static EOF (Kuo et al. 2008).

The section-time-mean velocity, solely due to the steady component u 0(y), is

$$ \langle\bar u\rangle=(2h)^{-1}\int\limits_{-h}^{h} u_0(y){\text d}y= U_{\rm HS}\frac{\hat{\psi}_{\rm AC}}{4}[\cos(\beta)+\cos(\gamma)] \left(1-\frac{\tanh(kh)}{kh}\right). $$
(18)

Note that under the conditions \(\beta=\gamma=0\) (full synchronization) and \(k\rightarrow\infty\) (very thin EDL), \(\langle\bar u\rangle\) is the maximum given by

$$ \max\langle\bar u\rangle=U_{\rm HS}\hat{\psi}_{\rm AC}/2. $$
(19)

The mean velocity vanishes under two conditions: \(\cos(\beta)+\cos(\gamma)=0\) or kh → 0. The first condition corresponds to \(|\beta\pm\gamma|=\pi,\) where the flow is split into forward and backward streams of equal flux, as has been explained above, while the second condition means that the EDL is infinitely thick, which is a limit we should in principle avoid since this will lead to overlapped EDLs and the Boltzmann distribution will no longer be valid as the datum for the potential is no longer in the channel (Qu and Li 2000; Shu et al. 2010). Although beyond the bound of our theory, the limit kh → 0 is considered here only to demonstrate the trend of the physical phenomena. The case of overlapped EDLs is beyond the scope of this study, and its effect on the axial mass dispersion needs to be determined in the future study.

4 Mass transport

The species to be transported through the carrier liquid is assumed neutral so that the transport phenomenon will not be affected by any of the electric potentials. The convection–diffusion equation governing the concentration C(x, y, t) of the diffusing substances can be written as

$$ \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} = D \left(\frac{\partial^2 C}{\partial {x}^2} + \frac{\partial^2 C}{\partial {y }^2} \right), $$
(20)

where D is the molecular diffusion coefficient. The non-penetrating boundary condition at the channel walls is given by

$$ \frac{\partial C}{\partial y}=0\quad\hbox{at}\quad y=\pm h. $$
(21)

In this study, we shall follow the homogenization technique (Mei et al. 1996), which is a multiple-scale method of averaging that can be used to derive directly the effective transport equations. In order to prepare grounds for perturbation analysis, the following assumptions are made regarding the scalings of the various physical quantities (Ng 2006):

  1. 1.

    Sufficiently long time has passed since the discharge of the solute into the flow so that the length scale for the longitudinal spreading of the solute is much greater than the width of the channel. It is meant that x = O(L) and y = O(h), where L is a characteristic longitudinal distance for the solute transport. The ratio

    $$ \epsilon=h/L\ll 1 $$

    is small enough to be used as an ordering parameter.

  2. 2.

    The oscillation period of the flow is so short that within this period there are no appreciable transport effects along the channel, though the effect of transverse diffusion is not negligible. The width of the channel is, however, so fine that diffusion across the entire cross section may be accomplished within this short time scale.

  3. 3.

    The Peclet number is equal to or greater than order of unity:

    $$ Pe\equiv h U_{\rm HS}/D \geq O(1). $$

These assumptions are quite relevant in the context of microfluidics. Normally, the microchannels have a large length-to-width aspect ratio (typically 1500:1) and cross-sectional dimensions of microfluidic channels can be as small as 100 μm (Ren et al. 2003). The oscillation period of the electric field is normally several milliseconds in AC EOF (Song et al. 2010). Also, microfluidic flows have typically a high Peclet number (Chang and Yang 2008). The Peclet number for liquid-based microchannel systems involving small species molecules can vary over a wide range from order one to several hundreds (Griffiths and Nilson 2000).

Under these assumptions, three distinct time scales may be defined as

$$ T_0=2\pi/\omega=O(h^2/D), $$
$$ T_1=L/U_{\rm HS}=T_0/\epsilon, $$
$$ T_2=L^2/D=T_0/\epsilon^2. $$

Based on these time scales, we may introduce accordingly

$$ t_{0}=t, \quad t_{1}=\epsilon t, \quad t_{2}=\epsilon^2 t $$

which are, respectively, the fast, medium, and slow time variables.

Note that our unsteady EOF is subjected to the constraint of an upper frequency limit for the validity of the static Poisson–Boltzmann equation. The theoretical bound of this model is the same as that of, among others, Huang and Lai (2006), Kuo et al. (2008), and Ramon et al. (2011). These authors have already looked into the time scale for the development of the Debye layer when the flow and/or electric fields are time oscillating. Huang and Lai (2006) and Ramon et al. (2011) have remarked that, although EOF is achievable for a wide range of frequencies, it is desirable if the frequency, ω/2π, is kept below 1 MHz to avoid EDL relaxation effects. Kuo et al. (2008) used the effective capacitance–resistance model to estimate the upper frequency to be of the range 0.3–0.8 MHz, depending on the electrolyte concentration and the dimension of the channel. A higher frequency is possible for an electrolyte of higher conductivity which enables a faster redistribution of the charges into equilibrium. The EDL can then be treated as in a thermal equilibrium state, when the driving frequency is substantially lower than the above-mentioned frequency limit. In order to safely ignore the transience associated with the development of the EDL, this study follows the previous studies as far as the upper limit of the driving frequency is concerned. It is assumed that the frequencies do not exceed 1 MHz. Like Ramon et al. (2011), a channel height in the order of 1–100 μm is considered. For the Stokes layer thickness to be comparable with the channel height, the corresponding range of the frequency is 0.3 MHz–30 Hz, which falls below the upper frequency limit. We further assume that the unsteady flow and electric fields considered here are not strong enough to significantly disturb the EDLs from equilibrium, or this model is to work in the low Dukhin limit (1993). An electric field less than 100 V/mm has been considered here, which was suggested in literature as an acceptable limit to avoid Joule heating and possible electrokinetic instability (Oddy et al. 2001; Morgan and Green 2003). An electric field of smaller magnitude, 10 V/mm, which is much weaker than the normal field induced by the EDL, was proposed by Kuo et al. (2008).

5 Asymptotic analysis and dispersion coefficients

The relative significance of the terms in the transport equation (20) with the boundary conditions are indicated below with the power of \(\epsilon{:}\,\)

$$ \frac{\partial C}{\partial t} +\epsilon u \frac{\partial C}{\partial x} = \epsilon^2 D \frac{\partial^2 C}{\partial {x}^2} + D\frac{\partial^2 C}{\partial {y }^2}, $$
(22)
$$ \frac{\partial C}{\partial y}=0\quad\hbox{at}\quad y=\pm h. $$
(23)

Following the asymptotic expansion introduced by Fife and Nicholes (1975), the concentration C is expressed as

$$ C(x,y,t)=C^{(0)}(x,y,t_{1},t_{2})+\epsilon C^{(1)}(x,y,t_{0},t_{1},t_{2})+\epsilon^2 C^{(2)}(x,y,t_{0},t_{1},t_{2})+O(\epsilon^3). $$
(24)

In this expansion, C (n)’s (n ≥ 1) are purely oscillatory functions of the short time variable t 0. It is anticipated that the oscillatory effect does not show up on the zeroth order, and therefore the leading order term is taken to be independent of this time variable. For the multiple-scale asymptotic analysis, the time derivative has been expanded as

$$ \frac{\partial}{\partial t}=\frac{\partial}{\partial t_{0}}+\epsilon \frac{\partial}{\partial t_{1}}+\epsilon^2 \frac{\partial}{\partial t_{2}}. $$
(25)

Using the expansions 24 and 25 in Eqs. 22 and 23 and equating the coefficients of like powers of ε from both sides, a system of differential equations is obtained.

5.1 Zeroth order

For the zeroth order O(1), Eqs. 22 and 23 give

$$ 0=D\frac{\partial^2 C^{(0)}}{\partial y^2}, \quad -h < y < h, $$
(26)
$$ \frac{\partial C^{(0)}}{\partial y}=0, \quad y=\pm h. $$
(27)

Equations 26 and 27 obviously imply that the leading order concentration is independent of y, i.e.,

$$ C^{(0)}=C^{(0)}(x, t_{1}, t_{2}). $$
(28)

5.2 First order

For the first order O(ε), Eqs. 22 and 23 give

$$ \frac{\partial C^{(0)}}{\partial t_{1}}+\frac{\partial C^{(1)}}{\partial t_{0}}+u\frac{\partial C^{(0)}}{\partial x}=D\frac{\partial^2 C^{(1)}}{\partial y^2}, \quad -h < y < h, $$
(29)
$$\frac{\partial C^{(1)}}{\partial y}=0, \quad y=\pm h. $$
(30)

Averaging the Eqs. 29 and 30 with respect to the fast-time variable t 0, we get

$$ \frac{\partial C^{(0)}}{\partial t_{1}}+u_0\frac{\partial C^{(0)}}{\partial x}=D\frac{\partial^2 \overline{C}^{(1)}}{\partial y^2}, \quad -h < y < h, $$
(31)
$$ \frac{\partial \overline{C}^{(1)}}{\partial y}=0, \quad y=\pm h, $$
(32)

where the overbar denotes time averaging (with respect to the fast-time variable t 0) over one period of oscillation and u 0 is the steady velocity component.

We further take cross-sectional average of Eq. 31 subjected to the condition 32 to produce

$$ \frac{\partial C^{(0)}}{\partial t_{1}}+\langle{u_0}\rangle\frac{\partial C^{(0)}}{\partial x}=0, $$
(33)

where the angle brackets denote spatial averaging across the channel section. Eliminating ∂C (0)/∂t 1 from Eqs. 29 and 33, we have

$$\frac{\partial C^{(1)}}{\partial t_{0}}+(u-\langle{u_0}\rangle)\frac{\partial C^{(0)}}{\partial x}=D\frac{\partial^2 C^{(1)}}{\partial y^2}, \quad -h < y < h. $$
(34)

Equation 34 suggests that C (1) is linearly proportional to ∂C (0)/∂x. Accordingly, the first-order concentration C (1) can be expressed as:

$$ C^{(1)}=\left(N(y)+\hbox{Re}[P(y)e^{i\omega t_0}]+\hbox{Re}[Q(y)e^{i(2\omega t_0+\beta)}]+\hbox{Re}[R(y)e^{i(2\omega t_0+\gamma)}]\right)\frac{\partial C^{(0)}}{\partial x}, $$
(35)

where the coefficients N(y), P(y), Q(y), and R(y) satisfy the boundary value problems given below.

Substituting Eq. 35 into Eqs. 34 and 30, and matching with the steady terms of the coefficient of ∂C (0)/∂x, we find the function N(y) to be governed by:

$$ D\frac{\text {d}^2 N}{\text {d} y^2}=u_0-\langle{u_0}\rangle, \quad -h < y < h, $$
(36)

with the boundary conditions

$$ \frac{\text {d}N}{\text {d}y}=0, \quad y=\pm h. $$
(37)

Again equating the terms associated with the harmonic components, we have the following equations and corresponding boundary conditions for the complex functions P(y), Q(y), and R(y).

Equation for P:

$$ D\frac{\text {d}^2 P}{\text {d} y^2}=i\omega P +u_1, \quad -h < y < h. $$
(38)

Boundary conditions:

$$ \frac{\text {d} P}{\text {d} y}=0, \quad y=\pm h. $$
(39)

Equation for Q:

$$ D\frac{\text {d}^2 Q}{\text {d} y^2}=2i\omega Q +u_2, \quad -h < y < h. $$
(40)

Boundary conditions:

$$ \frac{\text {d} Q}{\text {d} y}=0, \quad y=\pm h. $$
(41)

Equation for R:

$$ D\frac{\text {d}^2 R}{\text {d} y^2}=2i\omega R +u_3, \quad -h < y < h. $$
(42)

Boundary conditions:

$$ \frac{\text {d} R}{\text {d} y}=0, \quad y=\pm h. $$
(43)

5.3 Second order

For the second order O(ε2), Eqs. 22 and 23 give

$$ \frac{\partial C^{(0)}}{\partial t_{2}}+\frac{\partial C^{(1)}}{\partial t_{1}}+\frac{\partial C^{(2)}}{\partial t_{0}}+u\frac{\partial C^{(1)}}{\partial x}=D\frac{\partial^2 C^{(0)}}{\partial x^2}+D\frac{\partial^2 C^{(2)}}{\partial y^2}, \quad -h < y < h, $$
(44)
$$ \frac{\partial C^{(2)}}{\partial y}=0, \quad y=\pm h. $$
(45)

Averaging Eqs. 44 and 45 with respect to the fast-time variable t 0

$$ \frac{\partial C^{(0)}}{\partial t_{2}}+\frac{\partial \overline{C}^{(1)}}{\partial t_{1}}+\overline{u\frac{\partial C^{(1)}}{\partial x}}=D\frac{\partial^2 C^{(0)}}{\partial x^2}+D\frac{\partial^2 \overline{C}^{(2)}}{\partial y^2}, \quad -h < y < h, $$
(46)
$$ \frac{\partial\overline{C}^{(2)}}{\partial y}=0, \quad y=\pm h. $$
(47)

Now spatial averaging of Eq. 46 subjected to the condition 47 gives

$$ \frac{\partial C^{(0)}}{\partial t_{2}}+\frac{\partial \langle{\overline{C}^{(1)}}\rangle}{\partial t_{1}}+\left\langle{\overline{u\frac{\partial C^{(1)}}{\partial x}}}\right\rangle=D\frac{\partial^2 C^{(0)}}{\partial x^2}, \quad -h < y < h. $$
(48)

Using Eqs. 12 and 35, we have

$$ \begin{aligned} \overline{u\frac{\partial C^{(1)}}{\partial x}}=&\left[u_0 N+\frac{1}{2}\hbox{Re}(u_1 P^\ast)+\frac{1}{2}\hbox{Re}(u_2 Q^\ast)+{\frac{1}{2}}\hbox{Re}(u_3 R^\ast)\right.\\ &\left.+\frac{1}{2}\hbox{Re}(u_2 R^\ast)\cos(\beta-\gamma)-\frac{1}{2}\hbox{Im}(u_2 R^\ast)\sin(\beta-\gamma)\right.\\ &\left.+\frac{1}{2}\hbox{Re}(u_3 Q^\ast)\cos(\beta-\gamma)+\frac{1}{2}\hbox{Im}(u_3 Q^\ast)\sin(\beta-\gamma)\right]\frac{\partial^2 C^{(0)}}{\partial x^2}, \end{aligned} $$
(49)

where the asterisk denotes complex conjugates.

In deriving the expression 49, we have made use of the mathematical identity that the product of two harmonic functions of the same frequency will give rise to a steady component and a second-harmonic component. The time mean of the product gives, for any amplitudes a and b, the steady component:

$$ \overline{\hbox{Re}[a e^{i(\omega t+\beta)}] \hbox{Re}[b e^{i(\omega t+\gamma)}]}=\frac{1}{2}\hbox{Re}(a b^\ast) \cos(\beta-\gamma)-\frac{1}{2}\hbox{Im}(a b^\ast)\sin(\beta-\gamma). $$
(50)

Note that each of the three oscillatory flow components, which has a zero time mean itself, will give rise to a non-zero time-mean dispersion coefficient.

In order to find \(\overline{u\partial C^{(1)}/\partial x}\) using the expression 49, we need to solve Eqs. 38–43 for P, Q, and R. The normalized expressions of P, Q, and R, defined below, are given in the “Appendix”. It is interesting to find that

$$ u_{2} Q^\ast=u_{3} R^\ast\quad \hbox{ and }\quad u_{2} R^\ast=u_{3} Q^\ast. $$

Therefore the expression for \(\langle\overline{u \partial C^{(1)}/\partial x}\rangle\) reduces to

$$ \left\langle\overline{u\frac{\partial C^{(1)}}{\partial x}}\right\rangle =\left[\langle u_{0} N\rangle+\frac{1}{2}\hbox{Re}\langle u_{1} P^\ast\rangle +\hbox{Re}\langle u_{2}Q^\ast\rangle+\hbox{Re}\langle u_{3} Q^\ast\rangle \cos(\beta-\gamma)\right]\frac{\partial^2 C^{(0)}}{\partial x^2}. $$
(51)

Using Eqs. 12, 33, and 51 in Eq. 48, we get

$$ \begin{aligned} \frac{\partial C^{(0)}}{\partial t_{2}} =& \left[D + \langle{u_{0}}\rangle\langle{N}\rangle -\left\{\langle{u_{0} N}\rangle+\textstyle\frac{1}{2}\hbox{Re}\langle{u_{1} P^\ast}\rangle+\hbox{Re}\langle{u_{2} Q^\ast}\rangle\right.\right.\\ &\left.\left.+{\text{Re}}\langle{u_{3}Q^\ast}\rangle\cos(\beta-\gamma)\right\}\right] \frac{\partial^{2} C^{(0)}}{\partial x^{2}}. \end{aligned} $$
(52)

Combining Eqs. 33 and 52, the overall effective transport equation is obtained as follows (without the need to separate the time variables any more):

$$ \frac{\partial C^{(0)}}{\partial t}+\langle{u_{0}}\rangle \frac{\partial C^{(0)}}{\partial x}= [D + D_{\rm Ts}+D_{\rm Tw}]\frac{\partial^2 C^{(0)}}{\partial x^{2}}, $$
(53)

where

$$ D_{\rm Ts}=\langle{u_{0}}\rangle\langle{N}\rangle -\langle{u_{0} N}\rangle $$
(54)

is a dispersion coefficient due to steady part of the fluid motion, and

$$ \begin{aligned} D_{\rm Tw}=&-\frac{1}{2}\left[\hbox{Re}\langle{u_{1} P^\ast}\rangle+2 \hbox{Re}\langle{u_2 Q^\ast}\rangle+2 \hbox{Re}\langle{u_{3} Q^\ast}\rangle\cos(\beta-\gamma) \right] \end{aligned} $$
(55)

is a dispersion coefficient due to oscillatory part of the fluid motion.

The coefficient \(\langle{u_{0}}\rangle(=\langle{\overline{u}}\rangle)\) of ∂C (0)/∂x in Eq. 53 gives the speed of the convective motion of the solutes in the microchannel. It is therefore termed as the convection coefficient, which is already given in Eq. 18.

To derive explicit expressions for the dispersion coefficients, we first introduce the following normalized variables (distinguished by a caret):

$$ (\hat{N}, \hat{P}, \hat{Q}, \hat{R})=(N, P, Q, R)/ (U_{\rm HS}h^2/D), \quad \hat{u}=u/U_{\rm HS},\quad\hat{y}=y/h,\quad\hat{k}=k h, $$
$$ \hat{\lambda}=\lambda h=(1+i)/\hat\delta,\quad Sc=\nu/D,\quad\hat{\eta}=\eta h,\quad\hbox{ where } \quad \eta=\sqrt{{Sc}}\lambda,\quad\hat{\delta}=\delta/h, $$
$$ (\hat{D}_{\rm Ts},\hat{D}_{\rm Tw})=(D_{\rm Ts},\ D_{\rm Tw})/(U^2_{\rm HS}h^2/D). $$

Here, Sc is the Schmidt number, representing the ratio of molecular viscosity to molecular diffusivity. The parameters \(\hat k\) and \(\hat\delta\) are respectively the normalized Debye–Hückel parameter and the oscillation parameter.

The solution (in dimensionless form) of Eq. 36 subjected to the boundary conditions 37 is given by

$$ \begin{aligned} \hat{N}(\hat{y}) = &\hat{N}(-1)+\frac{\hat{\psi}_{\rm AC}}{4} [\cos(\beta)+\cos(\gamma)]\left[\frac{\tanh(\hat{k})}{2\hat{k}}\hat{y}^{2}-\frac{1}{\hat{k}^{2}} \frac{\cosh(\hat{k}\hat{y})}{\cosh(\hat{k})}-\frac{\tanh(\hat{k})}{2\hat{k}}+\frac{1}{\hat{k}^{2}}\right]\\ &+\frac{\hat{\psi}_{AC}}{4}[\cos(\beta)-\cos(\gamma)] \left[\frac{\hat{y}^{3}}{6}-\frac{\hat{y}}{2}+\frac{\coth(\hat{k})}{\hat{k}}\hat{y}\right.\\ &-\left.\frac{1}{\hat{k}^{2}}\frac{\sinh(\hat{k}\hat{y})}{ \sinh(\hat{k})}+\frac{\coth(\hat{k})}{\hat{k}}-\frac{1}{\hat{k}^{2}}-\frac{1}{3} \right], \end{aligned} $$
(56)

where \(\hat{N}(-1)\) is undetermined unless a uniqueness condition is specified. However, this uniqueness condition is not necessary as far as the dispersion coefficient \(\hat{D}_{\rm Ts}\) is concerned as the terms with \(\hat{N}(-1)\) cancel out to zero if Eq. 56 is substituted into Eq. 54.

Using Eqs. 13 and 56 in 54, we have the dimensionless form of the steady-flow-induced dispersion coefficient as

$$ \hat{D}_{\rm Ts}=\hat D_{\rm Ts1}+\hat D_{\rm Ts2}, $$
(57)

where

$$ \hat D_{\rm Ts1}= \left(\frac{\hat{\psi}_{\rm AC}}{4}\right)^{2} [\cos(\beta)+\cos(\gamma)]^{2}\left[2\frac{\tanh^{2}(\hat{k})}{\hat{k^{4}}}+\frac{5\tanh^{2}(\hat{k})} {6\hat{k}^{2}}-\frac{3\tanh(\hat{k})}{2\hat{k}^{3}}-\frac{1}{2\hat{k}^{2}}\right], $$
(58)

and

$$ \begin{aligned} \hat D_{\rm Ts2}=& \left(\frac{\hat{\psi}_{\rm AC}}{4}\right)^{2} [\cos(\beta)-\cos(\gamma)]^{2}\left[\frac{\coth(\hat{k})}{2\hat{k}^{3}} +\frac{3\coth^{2}(\hat{k})}{2\hat{k}^{2}}\right.\\ &-\left.\frac{2\coth(\hat{k})}{3\hat{k}}-\frac{2}{\hat{k}^{4}} -\frac{1}{2\hat k^{2}}+\frac{2}{15}\right]. \end{aligned} $$
(59)

This dispersion coefficient is a function of the Debye–Hückel parameter \(\hat{k},\) phases β and \(\gamma,\) and amplitude of oscillatory wall potentials \(\hat{\psi}_{\rm AC}.\) Note that this dispersion coefficient is a symmetrical function of the phase lags β and \(\gamma,\) although the steady component of velocity u 0 that gives rise to this dispersion coefficient is not symmetric with respect to β and \(\gamma.\)

In Eq. 57, we have decomposed \(\hat D_{\rm Ts}\) into two parts: the part that contains \([\cos(\beta)+\cos(\gamma)]^2\) is called \(\hat D_{\rm Ts1},\) and the part that contains \([\cos(\beta)-\cos(\gamma)]^{2}\) is called \(\hat D_{\rm Ts2}.\) It is easy to see that D Ts1 and D Ts2 are induced by the corresponding parts of \(\hat u_{0},\) which are respectively even and odd functions of \(\hat y.\) Let us recall our earlier remarks that convection is strong but dispersion is weak for a symmetrical velocity profile. On the contrary, convection is zero but dispersion is strong for an antisymmetrical velocity profile.

Some analytical properties of the coefficient \(\hat D_{\rm Ts}\) can be deduced as follows. First, for very small \(\hat k\to 0\) or a very thick EDL (let us consider this limit for demonstration of the trend even though this is beyond the regime of validity of the Boltzmann distribution), both parts of the dispersion coefficient vanish, \(\hat D_{\rm Ts}\rightarrow 0.\) Second, for very large \(\hat k\gg 1,\) the first part of the coefficient, \(\hat D_{\rm Ts1},\) vanishes, but the second part tends to a finite limit:

$$ \lim_{\hat k \to \infty} \hat{D}_{\rm Ts2}=\left(\frac{\hat{\psi}_{\rm AC}}{4}\right)^{2} \left[\cos(\beta)-\cos(\gamma)\right]^{2}\frac{2}{15}. $$
(60)

Thus for a very thin EDL, the steady-flow-induced dispersion coefficient is controlled by the factor \([\cos(\beta)-\cos(\gamma)]^2.\) It is important to note that this dispersion coefficient has the largest possible value

$$ \max\lim_{\hat k\to\infty}\hat{D}_{\rm Ts2} =\max\lim_{\hat k\to\infty}\hat{D}_{\rm Ts} =\hat{\psi}_{\rm AC}^{2}/30 $$
(61)

when \(\beta=0, \gamma=\pi\) or vice versa, i.e., one of the wall potentials being synchronized with the applied electric field and the other being π out of phase. This echoes with our earlier assertion that the dispersion arising from u 0 can be the largest when u 0 is an odd function of y, which has the steepest velocity gradient at the center of the channel. Third, by looking into the first derivative, we can find that the second part of the coefficient \(\hat D_{\rm Ts2}\) increases monotonically with \(\hat k,\) and hence the large-\(\hat k\)-limit given in Eq. 60 is indeed the absolute maximum of \(\hat D_{\rm Ts2}\) for given β and \(\gamma.\) The first part of the coefficient \(\hat D_{\rm Ts1}\) is a non-monotonic function of \(\hat k.\) It is zero at the two extremes of small and large \(\hat k,\) and has the maximum value given by

$$ \max \hat D_{\rm Ts1}=\left(\frac{\hat\psi_{\rm AC}}{4}\right)^{2}[\cos(\beta)+ \cos(\gamma)]^{2}(5.34\times 10^{-3})\quad \hbox{ at } \hat k=3.2963.$$
(62)

By virtue of these analytical properties, and also by comparing Eqs. 60 and 62, one can perceive that, with different choices of the phases β and \(\gamma, \hat D_{\rm Ts}\) can be set equal to either \(\hat D_{\rm Ts1}\) or \(\hat D_{\rm Ts2},\) where the former is in general much smaller than the latter. This provides one with the possibility to choose conditions that are either favorable or unfavorable to dispersion. We shall further look into the dependence of \(\hat D_{\rm Ts}\) on \(\beta, \gamma\) and \(\hat k\) in Sect. 6.

We next give the explicit expression for the oscillatory-flow-induced dispersion coefficient as given in Eq. 55. In this regard, we use the expressions for P, Q, and R that are given in the “Appendix”, and the velocity components u 1, u 2, and u 3 given by Eqs. 14–16, respectively. With some algebra, the dimensionless form of the oscillatory-flow-induced dispersion coefficient can be written as

$$ \hat{D}_{\rm Tw} =\hat{D}_{\rm Tw1}+\hat{D}_{\rm Tw2}, $$
(63)

where

$$ \hat{D}_{\rm Tw1} =-\hat{\psi}_{\rm DC}\frac{\hat{k}^{2}}{4}\hbox{Re}\left(\frac{A}{\hat{k}^{2}-\hat{\lambda}^{2}}\right), $$
(64)

and

$$ \hat{D}_{\rm Tw2}= -\hat{\psi}_{\rm AC}\frac{\hat{k}^{2}}{8} \left[\hbox{Re}\left(\frac{B}{\hat{k}^{2}-2\hat{\lambda}^{2}}\right) +\hbox{Re}\left(\frac{C}{\hat{k}^{2}-2\hat{\lambda}^{2}}\right)\cos(\beta-\gamma)\right], $$
(65)

in which the expressions for A, B, and C are too lengthy to be presented here, and are provided in the “Appendix”. The first component \(\hat{D}_{\rm Tw1}\) is due to the interaction of the oscillatory electric field with the steady component of the wall potentials, while the second component \(\hat{D}_{\rm Tw2}\) is the result of nonlinear interaction between the oscillatory components of the electric field and wall potentials. Like \(\hat D_{\rm Ts}, \hat D_{\rm Tw}\) is symmetric with respect to the phases β and \(\gamma.\) Also note that all the dispersion coefficient components are proportional to the square of the corresponding potential amplitude: \(\hat{D}_{\rm Ts}\sim \hat{\psi}_{\rm AC}^{2}, \hat{D}_{\rm Tw1}\sim \hat{\psi}_{\rm DC}^{2}, \hat{D}_{\rm Tw2} \sim \hat{\psi}_{\rm AC}^{2}.\)

6 Discussion of results

We have solved the problem for EOF and transport in a two-dimensional channel arising from an electric field interacting with two wall potentials, all oscillating at the same frequency, but with different phases. This non-linear interaction gives rise to a velocity distribution consisting of four components. One velocity component is steady contributing to the steady-flow-induced dispersion coefficient, and others are unsteady and they take part in the oscillatory-flow-induced dispersion. In the following, we shall look into various effects on the velocity components \(\hat{u}_{0}, \hat{u}_{1}, \hat{u}_{2},\) and \(\hat{u}_{3}\) (given by Eqs. 13–16, respectively, in dimensional form), and also their effects on the dispersion coefficient components \(\hat{D}_{\rm Ts}\) and \(\hat{D}_{\rm Tw}\) (given by Eqs. 57 and 63, respectively).

We summarize in Fig. 2 the relationships between the forcings and the velocity and dispersion coefficient components as a result of the interaction between the electric field and the wall potentials. These velocity and dispersion coefficients are functions of various controlling parameters, as noted in this figure.

Fig. 2
figure 2

The interaction between the oscillatory channel electric field E and the static and oscillatory wall potentials is to generate four velocity components, which give rise to three components of the dispersion coefficient. The parameters that control these velocity and dispersion coefficient components are noted in the figure

Full size image

In order to compute the steady component of velocity \(\hat{u}_{0}\) and the corresponding dispersion coefficient \(\hat{D}_{\rm Ts},\) we need to specify the phases \(\beta,\gamma\) and the Debye–Hückel parameter \(\hat{k}.\) Further, the oscillation parameter \(\hat{\delta}\) and the Schmidt number Sc need to be specified to compute the harmonic components \(\hat{u_{1}}, \hat{u}_{2}$\,{\text {and}}\, $\hat{u}_{3}\) of velocity and the associated dispersion coefficient \(\hat{D}_{\rm Tw}.\) The amplitude of oscillatory wall potentials \(\hat{\psi}_{\rm AC}\) and the static base component of the wall potentials \(\hat{\psi}_{\rm DC},\) which are linear or quadratic proportionality factors for the velocity and dispersion coefficient components, are also required for the computation.

It suffices for us to consider the phases to be in the range \(0\leq (\beta,\gamma)\leq \pi\) in our calculations. By periodicity of the sinusoidal functions, results for phases outside this range can be readily inferred from those within the range. The oscillation parameter \(\hat{\delta},\) which is the ratio of the Stokes boundary layer thickness to the half height of the channel, quantifies the frequency of flow oscillation. It is inversely proportional to the Womersley number. The number \(\hat{\delta}\) increases with the oscillation period. Therefore, higher the frequency, the smaller the value of \(\hat{\delta}.\) An order unity of the oscillation parameter \(\hat\delta=O(1)\) is assumed here. This is consistent with the frequency values used or reported by Huang and Lai (2006), Kuo et al. (2008), and Ramon et al. (2011). The inverse Debye length or the Debye–Hückel parameter \(\hat{k}\) characterizes the thickness of the EDL. Larger \(\hat k\) simply means a thinner EDL. For our calculations here, the range of Debye–Hückel parameter is taken as \(5\leq\hat{k}\leq 100.\) These values are frequently reported in the literature (Kuo et al. 2008; Ramon et al. 2011; Sadeghi and Saidi 2011). The Schmidt number appearing in the expression for \(\hat{D}_{\rm Tw},\) is the ratio of kinematic viscosity to molecular diffusivity. For aqueous solvents, the Schmidt number is of the order 103 (McEldoon and Datta 1992; Huang and Lai 2006), which is the value chosen here for the numerical calculations.

EOF and hence the associated transport phenomena depends on a large extent on the fabrication of electrodes used to generate the electric fields. Schasfoort et al. (1999) and van der Wouden et al. (2006) described the practical details of fabricating embedded gate electrodes on the microchannel walls for field effect flow control (FEFC). The gate electrodes, when covered with an insulator, can act as a wall. Applying a gate potential, the zeta potential in the gate region can be modified. The insulator, the Stern layer, and the double layer can be described by capacitors. Based on a three-capacitor-in-series model (Schasfoort et al. 1999), the influence of the gate potential on the local zeta potential can be calculated. van der Wouden et al. (2006) performed an analysis of the time scales involved in the dynamic behavior of an FEFC structure, and found that the rate of charging of the EDL can limit the upper operating frequency of the AC-switching of the potentials. The charging of the EDL is controlled by the series impedance of the channel resistance and the gate capacitance. The study of Kuo et al. (2008) can be referred to in this regard. For an aqueous NaCl electrolyte solution at 1 mM in a channel of height 1 μm, the characteristic resistance–capacitance (RC) charging time for the EDL was estimated by these authors to correspond to a maximum operating frequency of 0.3 MHz. This value can be increased by increasing the conductivity of the electrolyte or decreasing the size of the channel.

Figure 3a shows some profiles of the steady velocity component \(\hat{u}_{0}(\hat y)\) when the two wall potentials are in phase with each other (i.e., \(\beta=\gamma\)). The velocity features a symmetric distribution about the centerline of the channel \(\hat y=0.\) Maximum positive velocity attains when there is no phase difference between the channel electric field and the wall potentials, i.e., when all the oscillations are synchronized \((\beta=\gamma=0).\) With the increase of the phase lag, the velocity decreases in magnitude and finally vanishes everywhere when the lag equals π/2. Further increase of the phase lag produces back flow across the entire channel. The flow is the maximum negative when \(\beta=\gamma=\pi.\) The change of flow direction depending on the phase difference has been noted in the previous study by Kuo et al. (2008). The figure shows also the near-uniform behavior of the flow for a considerable portion of the channel section except near the channel walls where a no-slip condition is imposed. This symptom becomes more evident at larger values of \(\hat{k},\) i.e., for a thinner EDL, as can be seen from Fig. 3b. This is in sharp contrast to the pressure-driven flow where flow nonuniformity prevails across the entire channel section. As dispersion counts on the existence of a nonuniform flow profile, the dispersion for an EOF without sufficient velocity nonuniformity can be much weaker than that due to the pressure-driven flow of the same mean velocity.

Fig. 3
figure 3

Profiles of the steady velocity component \(\hat{u}_{0}(\hat y){:}\,\) a for equal phases of the wall potentials, \(\beta=\gamma,\) b for three different values of the Debye–Hückel parameter \(\hat{k},\) c for various values of \(\gamma\) when β = 0, and d Time-section-mean velocity, or the convection coefficient, as a function of \(\gamma\) for two different values of β

Full size image

Velocity profiles of \(\hat u_{0}(\hat y)\) are shown in Fig. 3b for three different values of the dimensionless Debye–Hückel parameter \(\hat{k},\) the number representing the inverse of the EDL thickness. For sufficiently small values of \(\hat{k},\) say \(\hat{k} < 1,\) the velocity distribution is approximately parabolic, close to that of Poiseuille flow. As the Debye–Hückel parameter \(\hat{k}\) increases, the velocity profile becomes more uniform in the core region, approaching the limit of a plug flow profile at very large \(\hat{k}.\) This is due to the fact that at higher values of \(\hat{k},\) the body force is more concentrated in the near-wall regions. These features of steady velocity component with varying \(\hat{k}\) are well known in the literature. The plug flow profile was experimentally verified by Taylor and Yeung (1993), Tallarek et al. (2000), and Herr et al. (2000), among others. On losing velocity differentials in the core region, the dispersion becomes weaker as \(\hat{k}\) increases. In the complete absence of shear, dispersion is identically zero in a plug flow as \(\hat{k}\rightarrow\infty.\)

Figure 3c shows profiles of \(\hat{u}_{0}(\hat y)\) for different values of \(\gamma,\) the phase difference between the channel electric field and the lower wall potential. The other phase β (phase difference between the channel electric field and the upper wall potential) is kept constant to be zero. The velocity shows an analogous behavior for varying values of β when \(\gamma\) is invariant. Clearly seen in the figure is asymmetry of the velocity profile about the centerline of the channel \(\hat y=0,\) which is expected as a result of unequal phases of the wall potentials. The zone of maximum velocity magnitude is shifted toward the upper wall when \(\gamma>\beta\) and to the lower wall region when \(\beta>\gamma\) (not shown in the figure). Thus, a greater phase lag repels the velocity distribution to the opposite wall. By theory, a phase difference of zero or π between the axial electric field and either or both of the wall potentials will drive the maximum interactive effect. It is of interest to note that, within the range of phase considered, a larger difference in the two phases will lead to larger nonuniformity of the velocity profile and hence may result in stronger dispersion. This is exemplified by the extremum case \(\beta=0, \gamma=\pi,\) in which the velocity \(\hat u_{0}\) is antisymmetric about \(\hat y=0;\) the forward flow over the upper half of the channel is exactly balanced by the backward flow over the lower half of the channel. In this case, \(\hat u_{0}\) produces zero net flow, and hence zero convection. The dispersion can be large, however, owing to a sharp velocity gradient as the velocity turns from positive to negative across the center of the channel. Therefore, the usual shortcoming of EOF in not producing sufficient dispersion may overcome by introducing wall potentials having disparate phases. The velocity nonuniformity is essentially determined by the phase difference \(|\beta-\gamma|.\) Within the range considered, the maximum possible phase difference occurs when one phase is zero, and the other phase is π. At such a maximum phase difference, the effect is more pronounced for larger \(\hat k.\) Therefore, contrary to the cases shown in Fig. 3b where \(\beta=\gamma=0,\) increasing \(\hat k\) can enhance dispersion when β = 0 and \(\gamma=\pi,\) or vice versa.

The asymmetry of the velocity as seen in Fig. 3c will induce net convective transport in the microchannel, which can be estimated by the convection coefficient given by \(\langle{u_0}\rangle=\langle{\overline{u}}\rangle\) in Eq. 18. Variations of this quantity are shown in Fig. 3d as a function of \(\gamma\) for two fixed values of β. As the convection coefficient is a symmetric function with respect to β and \(\gamma,\) Fig. 3d also holds good for fixed \(\gamma\) with varying β. For any value of dimensionless Debye–Hückel parameter \(\hat{k},\) the figure shows the monotonic change of the convection coefficient with the increase of \(\gamma.\) The conditions for the absolute minimum and the absolute maximum of the coefficient are \((\beta, \gamma)=(0, \pi)\) or (π, 0), and \((\beta, \gamma)=(0, 0)\) or (π, π), respectively. We shall immediately see that these conditions correspond to maximum and minimum values of the steady dispersion coefficient, respectively. In other words, minimum/maximum convection leads to maximum/minimum dispersion.

The first-harmonic velocity component \(\hat{u}_{1}(\hat y)\exp(i\omega t)\) results from the oscillatory axial electric field interacting with the steady component of the wall potentials. This is the only component which depends on the static base component \(\hat{\psi}_{\rm DC}\) of the wall potentials. Figure 4a shows profiles of the real part of the amplitude Re(\(\hat{u}_{1}\)) for different values of the oscillation parameter \(\hat{\delta}.\) At sufficiently small values of \(\hat{\delta}\) (≤0.1), corresponding to a thin Stokes layer or fast oscillation, the fluid is static in the core region, and only in the near-wall regions some flow develops in the Stokes layer. For larger \(\hat{\delta}\) or slower oscillation, the flow profile broadens somewhat into the center of the channel owing to a higher extent of viscous diffusion into the channel core. For very slow oscillation (\(\hat\delta\geq 1.5\)), the velocity amplitude profile becomes fully developed and resembles the velocity profile of steady flow: a nearly uniform profile in the core region. Symptoms are more evident for larger \(\hat{k}\) (not shown in this figure). Kuo et al. (2008) reported similar observations for small Strouhal number corresponding to large \(\hat{\delta}.\) For moderate \(\hat{\delta}\) (say ≈0.5), the velocity profile is an intermediate one between the two extremes; most of the flow is confined to the Stokes layer region and the fluid at the center of the channel falls behind. This agrees well with the observations made by Ramon et al. (2011) for increasing Womersley number which is inversely proportional to the oscillation parameter \(\hat{\delta}.\) The distribution of Re(\(\hat{u}_{1}\)) for different values of dimensionless Debye–Hückel parameter \(\hat{k}\) is shown in Fig. 4b. The velocity gradient near the wall becomes sharper as \(\hat{k}\) increases. As remarked by Huang and Lai (2006), the peak of the velocity distribution in the boundary region becomes smaller for smaller \(\hat{k}.\) This is because smaller \(\hat{k}\) (i.e., a larger Debye length) means that the counter-ions spread over a greater portion of the bulk liquid, and hence more fluid particles are to be dragged by the counter-ions. Figures 4c , d show similar dependence of the imaginary part Im(\(\hat{u}_{1}\)) on \(\hat\delta\) and \(\hat k.\)

Fig. 4
figure 4

Profiles of the oscillatory velocity component \(\hat{u}_{1}(\hat y)\): a the real part for four different values of the oscillation parameter \(\hat{\delta},\) b the real part for three different values of the Debye–Hückel parameter \(\hat{k},\) c the imaginary part for four different values of \(\hat{\delta},\) and d the imaginary part for three different values of \(\hat{k}\)

Full size image

The second-harmonic velocity components \(\hat{u}_{2}(\hat y)\exp[i(2\omega t+\beta)]\) and \(\hat{u}_{3}(\hat y)\exp[i(2\omega t+\gamma)]\) are due to the oscillatory axial electric field interacting with the oscillatory components of the upper and lower wall potentials, respectively. Figure 5a shows profiles of the real part of the velocity amplitude Re(\(\hat{u}_{2}\)) as a function of the oscillation parameter \(\hat{\delta}.\) The influence of the oscillatory electric potential of the lower wall is missing here. Velocity is appreciable only within the Stokes layer of the upper wall. In this region, the velocity increases with increasing oscillation parameter as the Stokes layer is thicker for slower oscillation. The velocity amplitude \(\hat{u}_{3}(\hat y)\) varies with \(\hat{\delta}\) in exactly the same manner as that of \(\hat{u}_{2}(\hat y)\) with the role of upper and lower walls interchanged. Figure 5b shows profiles of the real part of the velocity amplitude Re(\(\hat{u}_{3}\)) for different values of the dimensionless Debye–Hückel parameter \(\hat{k}.\) A thinner EDL results in a sharper decrease of the velocity near the wall. When the EDL is thicker, a greater part of the channel is influenced by the channel electric field and the velocity declines to zero more gradually. Here, the effect of the upper wall potential is absent, and the flow is confined to the Stokes layer adjacent to the lower wall. Again, the dependence of \(\hat{u}_{2}\) on \(\hat{k}\) is analogous to that of \(\hat{u}_{3}\) with the role of the walls interchanged. Figure 5c, d show similar dependence of the imaginary parts Im(\(\hat{u}_{2}\)) and Im(\(\hat{u}_{3}\)) on \(\hat\delta\) and \(\hat k.\)

Fig. 5
figure 5

Profiles of the oscillatory velocity components \(\hat{u}_{2}(\hat y)\) and \(\hat u_{3}(\hat y)(=\hat u_{2}(-\hat y))\): a the real part of \(\hat u_{2}\) for three different values of the oscillation parameter \(\hat{\delta},\) b the real part of \(\hat{u}_{3}\) for three different values of the Debye–Hückel parameter \(\hat{k},\) c the imaginary part of \(\hat u_{2}\) for three different values of \(\hat{\delta},\) d the imaginary part of \(\hat{u}_{3}\) for three different values of \(\hat{k}\)

Full size image

The two second-harmonic velocity components can be merged into one component when the two phases are the same: \(\beta=\gamma.\) In this case, the combined velocity amplitude, \(\hat u_{2}+\hat u_{3}, \) is given in Eq. 17. By superimposing the profiles shown in Fig. 5a–d onto their image counterparts (by flipping about the centerline y = 0), one can find that the combined velocity amplitude \(\hat u_{2}+\hat u_{3}\) has similar dependence on \(\hat\delta\) and \(\hat k\) as \(\hat u_{1}\) does. The relationship between \(\hat u_1\) and \(\hat u_{2}+\hat u_{3}\) can be readily checked by comparing Eq. 14 with Eq. 17. The main difference lies in a numerical factor of \(\sqrt{2}\) for the parameter λ. Compared with the first harmonics, the Stokes layer thickness for the second harmonics is reduced by a factor of \(\sqrt{2}\) because of the doubled frequency.

To see the aggregate effects of the velocity components, we show in Fig. 6a, b snap-shots of the total velocity profile \(\hat u(\hat y),\) given by Eq. 12, at several time instants within a half period for an equal amplitude of the DC and AC wall potentials. When \(\beta=\gamma=0,\) the velocity profile is symmetrical about the centerline, and the time-mean flux is non-zero. There are instants at which the profile has twin peaks, when dominated by that of the oscillatory flow components for which the velocity peak is in the Stokes layers. At other instants, the profile has the peak at the center, when dominated by that of the steady flow component. When β = 0 and \(\gamma=\pi,\) the mean flux is zero over one period of time. It is interesting to find that at some time instants, the flow is dominantly in the forward direction in the upper half of the channel, while at other times, the flow is dominated by backward flow in the lower half of the channel. On comparing the two cases shown in Fig. 6a, b, one can see that the flow is subjected to greater shear on the average across the channel in the second case \((\beta=0, \gamma=\pi)\) than in the first case \((\beta=\gamma=0)\). This is confirmed with the dispersion coefficient shown in the following figures.

Fig. 6
figure 6

Snap-shots of the combined velocity profile \(\hat u(\hat y)\) at various instants of time: a for zero phases of the wall potentials, \(\beta=\gamma=0,\) b for the maximum possible phase difference between the wall potentials, \(\beta=0, \gamma=\pi\)

Full size image

Having realized the influence of the controlling parameters on the velocity components, we now move to study the same on the dispersion coefficients. The dispersion coefficient \(\hat{D}_{\rm Ts},\) which is induced by the steady flow \(\hat u_{0},\) is shown in Fig. 7a as a function of the dimensionless Debye–Hückel parameter \(\hat{k}\) for some equal values of the phases: \(\beta=\gamma.\) Therefore, \(\hat D_{\rm Ts}=\hat D_{\rm Ts1}\) in this case. The corresponding profiles of \(\hat u_{0}\) are already shown in Fig. 3a. As remarked earlier, the coefficient \(\hat{D}_{\rm Ts1}\) is zero when \(\hat k=0,\) since the mean velocity \(\langle\hat u_{0}\rangle\) vanishes at this theoretical limit of infinitely large Debye length. As \(\hat k\) increases, \(\langle\hat u_{0}\rangle\) increases, and therefore \(\hat{D}_{\rm Ts1}\) increases as well. As already shown earlier, the coefficient \(\hat{D}_{\rm Ts1}\) reaches a maximum at \(\hat k=3.2963,\) as given in Eq. 62. Further increasing \(\hat k\) will, however, lead to a more uniform velocity profile in the core region of the channel, and thereby decrease the dispersion coefficient. The coefficient \(\hat{D}_{\rm Ts1}\) will ultimately tend to zero when \(\hat k\gg 1,\) as the flow becomes a plug flow at the limit of an infinitely thin EDL.

Fig. 7
figure 7

The steady-flow-induced component of the dispersion coefficient \(\hat D_{\rm Ts}\): a as a function of \(\hat{k}\) for some equal values of the phases of the wall potentials, \(\beta=\gamma,\) b as a function of \(\hat{k}\) for different values of \(\gamma\) when β = 0, c continuous variations of \(\hat D_{\rm Ts}\) with \(\gamma\) for two fixed values of β

Full size image

We further show in Fig. 7b \(\hat{D}_{\rm Ts}\) as a function of \(\hat{k}\) for some unequal values of the phases: β = 0 and \(0\leq \gamma\leq \pi.\) Note that \(\hat D_{\rm Ts}\) is contributed by the two parts, \(\hat D_{\rm Ts1}\) and \(\hat D_{\rm Ts2},\) according to the proportionality factors of \([\cos(\beta)+\cos(\gamma)]^{2}\) and \([\cos(\beta)-\cos(\gamma)]^{2}, \) respectively. Hence, for the two limiting phases, \(\hat{D}_{\rm Ts}=\hat D_{\rm Ts1}\) when \(\gamma=0,\) and \(\hat{D}_{\rm Ts}=\hat D_{\rm Ts2}\) when \(\gamma=\pi.\) The former varies non-monotonically with \(\hat k,\) while the latter increases monotonically with \(\hat k.\) As evidently seen in Fig. 7b, \(\hat D_{\rm Ts2}\gg \hat D_{\rm Ts1},\) especially for \(\hat k\gg 1.\) The absolute maximum \(\hat D_{\rm Ts},\) which occurs when \(\gamma=\pi\) and \(\hat k\to\infty,\) is already given in Eq. 61: \(\max\hat D_{\rm Ts}=\hat{\psi}_{\rm AC}^2/30.\)

Figure 7c shows the continuous variations of \(\hat D_{\rm Ts}\) with the phase \(0\leq \gamma\leq \pi,\) for the two limiting values of β = 0, π. This figure reveals that the dispersion coefficient is negligibly small when the phase difference \(|\beta-\gamma|\) is smaller than π/6, for which the first part \(\hat D_{\rm Ts1}\) is dominant. The dispersion coefficient increases dramatically when the phase difference \(|\beta-\gamma|\) increases beyond π/6, for which the second part \(\hat D_{\rm Ts2}\) becomes increasingly dominant.

We finally show in Fig. 8a, b the oscillatory-flow-induced dispersion coefficient \(\hat D_{\rm Tw}\) as a function of the oscillation parameter \(\hat\delta\) and the Debye–Hückel parameter \(\hat{k}\) for \(\beta=\gamma=0.\) The solid lines are for cases solely due to the DC wall potential and hence are for the coefficient \(\hat D_{\rm Tw1}.\) The dashed lines are for cases solely due to the AC wall potential and hence are for the coefficient \(\hat D_{\rm Tw2}.\) The following observations can be made based on these figures. First, \(\hat D_{\rm Tw}\) increases monotonically with \(\hat\delta.\) In other words, the dispersion coefficient is larger for slower oscillation, which is consistent with the understanding well known in the literature (e.g., Ng 2006). Second, \(\hat D_{\rm Tw}\) varies non-monotonically with \(\hat k.\) It is zero for both small and large \(\hat k,\) and attains a maximum at a finite value of \(\hat k\approx 30{-}50\) depending on \(\hat\delta.\) This behavior resembles that exhibited by \(\hat D_{\rm Ts1},\) and therefore can be explained likewise. Third, for equal amplitudes \(\hat\psi_{\rm DC}=\hat\psi_{\rm AC},\) the \(\hat\psi_{\rm DC}\)-induced component \(\hat D_{\rm Tw1}\) is in general much larger than, by two orders of magnitude, the \(\hat\psi_{\rm AC}\)-induced component \(\hat D_{\rm Tw2}.\) Therefore, as long as \(\hat\psi_{\rm AC}\sim\hat\psi_{\rm DC},\) \(\hat D_{\rm Tw2}\) can be ignored when compared with \(\hat D_{\rm Tw1}.\) Fourth, by comparing with the values shown in Fig. 7b, it is also evident that for equal amplitudes \(\hat\psi_{\rm DC}=\hat\psi_{\rm AC},\) the oscillatory-flow-induced dispersion coefficient \(\hat D_{\rm Tw}\) is much smaller than the steady-flow-induced dispersion coefficient \(\hat D_{\rm Ts}.\) Therefore, as long as \(\hat\psi_{\rm AC}\sim\hat\psi_{\rm DC},\) neither \(\hat D_{\rm Tw1}\) nor \(\hat D_{\rm Tw2}\) is significant when compared with \(\hat D_{\rm Ts},\) and one can safely ignore these oscillatory-flow-induced components when evaluating the dispersion coefficient.

Fig. 8
figure 8

The oscillatory-flow-induced component of the dispersion coefficient \(\hat D_{\rm Tw}{:}\,\) a as a function of the oscillation parameter \(\hat{\delta}\) for three different values of the Debye–Hückel parameter \(\hat{k},\) b as a function of \(\hat{k}\) for different values of \(\hat{\delta}\)

Full size image

7 Concluding remarks

Steady EOF driven by static electric forcings is known to be associated with small dispersion owing to its nearly plug flow profile. This is desirable for processes like separation of species in which dispersion is unwanted. In other processes like chemical reactions in which mixing of reactants is needed, dispersion is desired. Therefore, it is of practical value if an EOF mechanism can be devised such that the flow can produce either negligible or appreciable dispersion depending on values of the controlling parameters.

In this article, we have looked into one kind of such a mechanism. This mechanism, studied previously by Kuo et al. (2008), is to generate steady directional EOF by the nonlinear interaction between oscillatory axial electric field and oscillatory wall potentials. The phases, relative to that of the channel electric field, of the wall potentials are of significance here. Allowing disparate phases of the two wall potentials, we have examined in detail the effect of the two phases on the velocity as well as the dispersion coefficient components. In the usual case when both phases are zero (i.e., full synchronization of the wall potentials with the channel electric field), the dispersion coefficient is indeed very small, vanishing identically for infinitely thin EDLs. It is remarkable that when one phase is zero and the other is π (i.e., the maximum possible phase difference), the dispersion coefficient becomes appreciable as it reaches the largest possible value, attaining the absolute maximum at the limit of infinitely thin EDLs. This absolute maximum, given in Eq. 61, is a significant result derived in this article.