Multiscale bio-chemo-mechanical model of intimal hyperplasia

Abstract

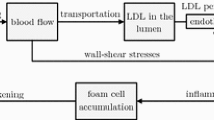
We consider a computational multiscale framework of a bio-chemo-mechanical model for intimal hyperplasia. With respect to existing models, we investigate the interactions between hemodynamics, cellular dynamics and biochemistry on the development of the pathology. Within the arterial wall, we propose a mathematical model consisting of kinetic differential equations for key vascular cell types, collagen and growth factors. The luminal hemodynamics is modeled with the Navier–Stokes equations. Coupling hypothesis among time and space scales are proposed to build a tractable modeling of such a complex multifactorial and multiscale pathology. A one-dimensional numerical test-case is presented for validation by comparing the results of the framework with experiments at short and long timescales. Our model permits to capture many cellular phenomena which have a central role in the physiopathology of intimal hyperplasia. Results are quantitatively and qualitatively consistent with experimental findings at both short and long timescales.

Appendices

Appendix A: Analytical development about diffusion–reaction equation

1.1 Appendix A.1: Dimensional analysis

We use cylindrical coordinates $(r,\theta ,z)$, with r the radius, $\theta$ the polar angle, and z the axial coordinate. The unsteady diffusion–reaction equation that describes the evolution of the concentration C of a growth factor (GF) x within an idealized arterial wall, which assumes the only radial dependence of C, is

$$\begin{aligned} \frac{\partial C}{\partial t} = \frac{D}{r} \frac{\partial }{\partial r} \left( r \frac{\partial C}{\partial r} \right) - k C \quad \mathrm {in} \; \varOmega _{w}. \end{aligned}$$

(34)

D is the x diffusion coefficient within the arterial wall, and k is the consumption rate of the medium. The idealized arterial wall and domain $\varOmega _w$ are described in Fig. 1.

The dimensionless unsteady diffusion–reaction equation reads

$$\begin{aligned} \frac{L^2}{T_{\mathrm {gr}}D}\frac{\partial C^\dagger }{\partial t^\dagger } = \frac{1}{r^\dagger }\frac{\partial }{\partial r^\dagger } \left( r^\dagger \frac{\partial C^\dagger }{\partial r^\dagger } \right) - k^\dagger C^\dagger \quad \mathrm {in} \; \varOmega _{w}, \end{aligned}$$

(35)

with the dimensionless variables

$$\begin{aligned} C^\dagger = \frac{C}{\widetilde{C}},\quad r^\dagger =\frac{r}{L} , \quad t^\dagger =\frac{t}{T_{\mathrm {gr}}}. \end{aligned}$$

(36)

$\widetilde{C}$, L and $T_{\mathrm {gr}}$ are a characteristic concentration, a characteristic diffusion length and a characteristic growth timescale. The dimensionless consumption is $k^\dagger =k L^2/D$, and the dimensionless ratio $L^2/(T_{\mathrm {gr}}D)$ expresses diffusion timescale versus growth timescale.

Upon assuming short growth timescale $T_{\mathrm {gr}} \sim {1}$ day, thickness of arterial wall $L={500}$ $\upmu$m and NO diffusion coefficient $D= {8.48 \times 10^{-10}}$ m$^{2}$ s$^{-1}$ , the dimensionless number $L^2/(T_{\mathrm {gr}}D)= {3 \times 10^{-3}}$ remains much lower than one. According to this, we can remove the time-dependent term in Eq. (34)—this was also done in Goodman et al. (2016)—and we get the following steady diffusion reaction

$$\begin{aligned} \frac{D}{r} \frac{\mathrm {d}}{\mathrm {d} r} \left( r \frac{\mathrm {d} C}{\mathrm {d} r} \right) - k C = 0 \quad \mathrm {in} \; \varOmega _{w}. \end{aligned}$$

(37)

Note that even accounting for a transitional timescale of endothelial cells (ECs) adaptation to hemodynamics, which would be much smaller than $T_{\mathrm {gr}}$ as $T_{\mathrm {tr}}\sim 1 \,\mathrm {h}$ (Hahn and Schwartz 2009), the time derivative term in (34) remains negligible ($L^2/(T_{\mathrm {tr}}D)={8 \times 10^{-2}}$).

1.2 Appendix A.2: Development of source term expression

The complete problem to be solved is Eq. (37) plus the following Neumann boundary conditions

$$\begin{aligned} -D\left. \frac{\mathrm {d} C}{\mathrm {d} r} \right| _{r=R_{\mathrm {l}}}&=B \quad \mathrm {at} \quad r=R_{\mathrm {l}}, \end{aligned}$$

(38a)

$$\begin{aligned} \left. \frac{\mathrm {d} C}{\mathrm {d} r} \right| _{r=R_{\mathrm {ext}}}&=0 \quad \mathrm {at} \quad r=R_{\mathrm {ext}}, \end{aligned}$$

(38b)

to model ECs influence on the x GF bioavailability within arterial layers. Equations (38a) and (38b) are, respectively, a flux conservation condition (see Eq. (23)) and a no flux condition at external arterial radius.

Equation (37) is a Bessel equation, whose solution with boundary conditions (38) is

$$\begin{aligned} C(r) = \frac{B}{\kappa D} \frac{I_1(\kappa R_{\mathrm {ext}}) K_0(\kappa r) + K_1(\kappa R_{\mathrm {ext}}) I_0(\kappa r) }{K_1(\kappa R_{\mathrm {l}}) I_1(\kappa R_{\mathrm {ext}}) - I_1(\kappa R_{\mathrm {l}}) K_1(\kappa R_{\mathrm {ext}})} \end{aligned}$$

(39)

with $\kappa ^2=k/D$, $I_{0,1}, \; K_{0,1}$ modified Bessel functions of first and second kind. The vector mass flux comes from Fick’s law $\varvec{J} = -D \varvec{\nabla } C$, and its amplitude in the radial direction $\varvec{n}$ comes from (39) as

$$\begin{aligned} J&= (-D \varvec{\nabla } C) \cdot \varvec{n}\\&= B \frac{I_1(\kappa r) K_1(\kappa R_{\mathrm {ext}}) - K_1(\kappa r)I_1 (\kappa R_{\mathrm {ext}}) }{I_1(\kappa R_{\mathrm {l}}) K_1(\kappa R_{\mathrm {ext}}) - K_1(\kappa R_{\mathrm {l}}) I_1(\kappa R_{\mathrm {ext}})}. \end{aligned}$$

(40)

To define the source term of the generic Eq. (14), we integrate J over the surface of length $\varDelta z$ at radius r, which amounts to multiplying by $2 \pi r \varDelta z$ as

$$\begin{aligned} m(r) = 2 \pi r \varDelta z \; B \frac{I_1(\kappa r) K_1(\kappa R_{\mathrm {ext}}) - K_1(\kappa r) I_1(\kappa R_{\mathrm {ext}}) }{I_1(\kappa R_{\mathrm {l}}) K_1(\kappa R_{\mathrm {ext}}) - K_1(\kappa R_{\mathrm {l}}) I_1(\kappa R_{\mathrm {ext}})}. \end{aligned}$$

(41)

m is the production rate of GF as a function of the radial coordinate. To get average production rates of GF x over the layers considered , namely the intima and the media, Eq. (41) is integrated over the layers thicknesses, as in (15). This averaging procedure and the radial variation of $m^{x}$ are shown in Fig. 11.

Fig. 11

$m^{x}$ from Eq. (41) for $r\in [R_{\mathrm {l}},R_{\mathrm {EEL}}]$. The averaged values of $m^{x}$ (from Eq. (15)) within intima and media layers, $\bar{M}^{x}_{\mathrm {i,m}}$, are represented with dashed lines

Appendix B: Dynamics of growth factors

For reference, we show in Fig. 12 the evolution of all the GFs in both media and intima layers for the test-case presented in Sect. 3, between 0 and 30 days. The initial damage of ECs layer causes a subexpression of NO amount (Lemson et al. 2000) and overexpression of other GFs at short timescale (Ducasse et al. 2003). There are two main types of time evolution for GFs, that of NO and that of other GFs (PDGF, FGF, Ag, TGF, TNF, MMP). From an analysis of biochemical equations, the NO is not involved in inter-GFs coupling mechanisms, so its dynamics is mainly driven by hemodynamics stimuli. This is seen between 6 and 30 days, where there is a net increase in NO amount within intima layer corresponding to the luminal narrowing phase (as WSS increases, so does the production rate). In the second group, a different type of temporal evolution is seen because this group is strongly coupled (seen Table 2). They evolve globally in the same way with an increase in the short time induced by the denudation of the endothelium and a decrease below the equilibrium value $\delta ^{\mathrm {GFs}}=1.0$ around day 21 which corresponds to the turning point ($r_{\mathrm {i}} < 0$) discussed in Sect. 3.2.

Fig. 12

Time evolution of dimensionless GFs amounts $\delta ^x=\eta ^x/\widetilde{\eta }$ in (–) within intima (solid lines) and media (solid lines with symbols) layers between 0 and 30 days

Appendix C: Final equilibrium state of the test-case

The final equilibrium state of the denudation test-case developed in Sect. 3 is presented in Table 5. We provide the vector of variables $\varvec{y}$ of (18) as $\varvec{y}^\dagger = \varvec{y} / \varvec{y}^{\mathrm {ref}}$ where $\varvec{y}^\dagger$ is the vector of rescaled or dimensionless variables by its initial–physiological values $\varvec{y}^{\mathrm {ref}}$.

Table 5 New state of equilibrium reached after $t_f\simeq$ 1107, days ($\simeq 37$ months) presented in terms of rescaled and dimensionless variables $y^\dagger = y/y^{\mathrm {ref}}$, with $y^{\mathrm {ref}}$ the initial-physiological value