Mimetization of the elastic properties of cancellous bone via a parameterized cellular material

Abstract

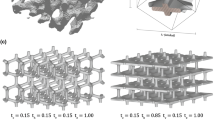
Bone tissue mechanical properties and trabecular microarchitecture are the main factors that determine the biomechanical properties of cancellous bone. Artificial cancellous microstructures, typically described by a reduced number of geometrical parameters, can be designed to obtain a mechanical behavior mimicking that of natural bone. In this work, we assess the ability of the parameterized microstructure introduced by Kowalczyk (Comput Methods Biomech Biomed Eng 9:135–147, 2006. doi:10.1080/10255840600751473) to mimic the elastic response of cancellous bone. Artificial microstructures are compared with actual bone samples in terms of elasticity matrices and their symmetry classes. The capability of the parameterized microstructure to combine the dominant isotropic, hexagonal, tetragonal and orthorhombic symmetry classes in the proportions present in the cancellous bone is shown. Based on this finding, two optimization approaches are devised to find the geometrical parameters of the artificial microstructure that better mimics the elastic response of a target natural bone specimen: a Sequential Quadratic Programming algorithm that minimizes the norm of the difference between the elasticity matrices, and a Pattern Search algorithm that minimizes the difference between the symmetry class decompositions. The pattern search approach is found to produce the best results. The performance of the method is demonstrated via analyses for 146 bone samples.

Appendices

Appendix

1.1 Human samples

Figure 11 depicts the residual $\mathcal {R}_{1}$ and the symmetry class errors (18) of the SQP optimizations as functions of BV/TV. Figure 11a shows that $\mathcal {R}_{1}$ and its dispersion diminish sharply with BV/TV, from $0.5\lesssim \mathcal {R}_{1}\lesssim 3$ for $\hbox {BV}/\hbox {TV}<7.5\%$ to $0.1\lesssim \mathcal {R}_{1}\lesssim 0.6$ for $\hbox {BV}/\hbox {TV}>32\%$. The relaxation of the $\hbox {BV}/\hbox {TV}_\mathrm{tol}$ constrain does not result in significant improvements in $\mathcal {R}_{1}$ (results not reported here for analyses performed for $\hbox {BV}/\hbox {TV}_\mathrm{tol}=10\%$ exhibit the same behavior). Results in Fig. 11b allow to observe that $c_\mathrm{iso}$ and $c_\mathrm{hex}$ are systematically over and underestimated, respectively; their mean errors are $\overline{e_{c_\mathrm{iso}}}=0.20$ and $\overline{e_{c_\mathrm{hex}}}=-0.74$. Errors tend to decrease with BV/TV, the only exception is that of the tetragonal symmetry, which can attain values over the range $-5<e_{c_\mathrm{tet}}<12$. Mean relative errors for the tetragonal and the orthorhombic symmetry classes are $\overline{e_{c_\mathrm{tet}}}=1.74$ and $\overline{e_{c_\mathrm{ort}}}=0.18$, respectively.

Fig. 11

SQP optimization of human samples: a residuals and b symmetry class errors as functions of BV/TV

The PS optimization resulted in a mean value for the residual $\overline{\mathcal {R}_{2}}=0.06$ with standard deviation $\hbox {SD}_{\mathcal {R}_{2}}=0.09$. Like for the SQP approach, the relaxation of the $\hbox {BV}/\hbox {TV}_\mathrm{tol}$ constrain did not result in significant improvements for $\mathcal {R}_{2}$. In addition to the error for the elasticity matrices shown in Figs. 9. Figure 12 presents the errors (18) for the symmetry classes. Figure 12 allows to observe that mean errors for the symmetry classes are much lower than those of the SQP approach in Fig. 11b: $\overline{e_{c_\mathrm{iso}}}=0.06$, $\overline{e_{c_\mathrm{hex}}}=-0.13$, $\overline{e_{c_\mathrm{tet}}}=-0.06$ and $\overline{e_{c_\mathrm{ort}}}=-0.02$; standard deviations are $(\hbox {SD}_{e_\mathrm{iso}}=0.11)$, $(\hbox {SD}_{e_\mathrm{hex}}=0.27)$, $(\hbox {SD}_{e_\mathrm{tet}}=1.67)$ and $(\hbox {SD}_{e_\mathrm {ort}}=0.18)$. Like for the SQP optimization, $e_{c_\mathrm{tet}}$ presents the largest dispersion and there are tendencies to overestimate $c_\mathrm{iso}$ and to underestimate $c_\mathrm{hex}$. The high dispersion of $e_{c_\mathrm{tet}}$ is consequence of the small relative contribution of the tetragonal symmetry to the elasticity matrix, which is always $c_\mathrm{tet}<0.05$, see Table 3 and Fig. 1.

Fig. 12

PS optimization of human samples: symmetry class error as function of BV/TV

Bovine Samples

Target elastic matrices of the bovine femoral samples

$$\begin{aligned} \mathbb {C}_{b_{1} }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.268} &{} {0.087} &{} {0.152} &{} {-0.015} &{} {-0.011} &{} {-0.003} \\ {0.087} &{} {0.486} &{} {0.195} &{} {0.001} &{} {-0.066} &{} {0.023} \\ {0.152} &{} {0.195} &{} {0.677} &{} {0.010} &{} {0.044} &{} {0.011} \\ {-0.015} &{} {0.001} &{} {0.010} &{} {0.175} &{} {-0.042} &{} {-0.005} \\ {-0.011} &{} {-0.066} &{} {0.044} &{} {-0.042} &{} {0.198} &{} {0.001} \\ {-0.003} &{} {0.023} &{} {0.011} &{} {-0.005} &{} {0.001} &{} {0.112} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(24)

$$\begin{aligned} \mathbb {C}_{b_{2} }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.306} &{} {0.152} &{} {0.199} &{} {0.060} &{} {-0.010} &{} {-0.010} \\ {0.152} &{} {1.202} &{} {0.421} &{} {-0.025} &{} {0.039} &{} {0.052} \\ {0.199} &{} {0.421} &{} {1.885} &{} {-0.040} &{} {0.067} &{} {0.007} \\ {0.060} &{} {-0.025} &{} {-0.040} &{} {0.461} &{} {-0.089} &{} {-0.149} \\ {-0.010} &{} {0.039} &{} {0.067} &{} {-0.089} &{} {0.268} &{} {0.064} \\ {-0.010} &{} {0.052} &{} {0.007} &{} {-0.149} &{} {0.064} &{} {0.256} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(25)

$$\begin{aligned} \mathbb {C}_{b_{3} }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.573} &{} {0.234} &{} {0.219} &{} {-0.006} &{} {-0.015} &{} {0.004} \\ {0.234} &{} {0.640} &{} {0.253} &{} {-0.005} &{} {-0.016} &{} {0.006} \\ {0.219} &{} {0.253} &{} {1.260} &{} {-0.017} &{} {0.023} &{} {-0.003} \\ {-0.006} &{} {-0.005} &{} {-0.017} &{} {0.317} &{} {-0.017} &{} {-0.002} \\ {-0.015} &{} {-0.016} &{} {0.023} &{} {-0.017} &{} {0.246} &{} {0.052} \\ {0.004} &{} {0.006} &{} {-0.003} &{} {-0.002} &{} {0.052} &{} {0.224} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(26)

$$\begin{aligned} \mathbb {C}_{b_{4} }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.163} &{} {0.075} &{} {0.068} &{} {-0.008} &{} {-0.016} &{} {0.010} \\ {0.075} &{} {0.350} &{} {0.126} &{} {-0.018} &{} {-0.005} &{} {0.018} \\ {0.068} &{} {0.126} &{} {0.606} &{} {0.029} &{} {-0.004} &{} {-0.032} \\ {-0.008} &{} {-0.018} &{} {0.029} &{} {0.148} &{} {-0.023} &{} {0.043} \\ {-0.016} &{} {-0.005} &{} {-0.004} &{} {-0.023} &{} {0.093} &{} {-0.014} \\ {0.010} &{} {0.018} &{} {-0.032} &{} {0.043} &{} {-0.014} &{} {0.110} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(27)

$$\begin{aligned} \mathbb {C}_{b_{5} }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.318} &{} {0.075} &{} {0.107} &{} {-0.008} &{} {0.001} &{} {0.021} \\ {0.075} &{} {0.426} &{} {0.182} &{} {0.024} &{} {0.002} &{} {-0.017} \\ {0.107} &{} {0.182} &{} {0.464} &{} {-0.027} &{} {-0.003} &{} {-0.001} \\ {-0.008} &{} {0.024} &{} {-0.027} &{} {0.144} &{} {-0.007} &{} {0.002} \\ {0.001} &{} {0.002} &{} {-0.003} &{} {-0.007} &{} {0.116} &{} {0.008} \\ {0.021} &{} {-0.017} &{} {-0.001} &{} {0.002} &{} {0.008} &{} {0.114} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \nonumber \\ \end{aligned}$$

(28)

The PS optimization of each sample was run ten times using different seeds. For each case, the best two outcomes (these are, the solutions that achieve the lowest values of the objective function) were compared to assess the repeatability of the solutions. It was found that for Samples #2 and #4, the residuals of the best two solutions are almost coincident (they differ less than 1%), while the resultant values for the geometrical parameters coincide within 2%. For samples #1 and #3, the lowest two residuals differ in around 12% and the geometrical parameters have discrepancies of up to 80%. It is interesting to note that the parameter $t_{e}$, the one which governs microstructure orthotropy, showed a remarkable repeatability, it presented discrepancies within 0.2% for the analyses of Samples #1, #2, #3 and #4. In contrast, for Sample #5, residuals of the best two solutions differ in nearly 90% and the geometrical parameters up to 70%; the best performance is for $t_{e}$, which presents a discrepancy discrepancy of 13%. The behavior for $t_{e}$ could be explored as a mean for the refinement of the optimization procedure.

Finally, the resultant elastic matrices for the mimetic parameterized microstructures are:

$$\begin{aligned} \mathbb {C}_{b_{1} }^{\prime }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.302} &{} {0.204} &{} {0.105} &{} 0 &{} 0 &{} 0 \\ {0.204} &{} {0.502} &{} {0.156} &{} 0 &{} 0 &{} 0 \\ {0.105} &{} {0.156} &{} {0.669} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {0.147} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {0.116} &{} 0 \\ 0 &{} {0} &{} 0 &{} 0 &{} 0 &{} {0.081} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(29)

$$\begin{aligned} \mathbb {C}_{b_{2} }^{\prime }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.268} &{} {0.087} &{} {0.152} &{} 0 &{} 0 &{} 0 \\ {0.087} &{} {0.486} &{} {0.195} &{} 0 &{} 0 &{} 0 \\ {0.152} &{} {0.195} &{} {0.677} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {0.175} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {0.198} &{} 0 \\ 0 &{} {0} &{} 0 &{} 0 &{} 0 &{} {0.112} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(30)

$$\begin{aligned} \mathbb {C}_{b_{3} }^{\prime }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.566} &{} {0.316} &{} {0.224} &{} 0 &{} 0 &{} 0 \\ {0.316} &{} {0.709} &{} {0.261} &{} 0 &{} 0 &{} 0 \\ {0.224} &{} {0.261} &{} {1.201} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {0.290} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {0.261} &{} 0 \\ 0 &{} {0} &{} 0 &{} 0 &{} 0 &{} {0.132} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(31)

$$\begin{aligned} \mathbb {C}_{b_{4} }^{\prime }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.179} &{} {0.163} &{} {0.079} &{} 0 &{} 0 &{} 0 \\ {0.143} &{} {0.377} &{} {0.133} &{} 0 &{} 0 &{} 0 \\ {0.079} &{} {0.133} &{} {0.569} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {0.125} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {0.092} &{} 0 \\ 0 &{} {0} &{} 0 &{} 0 &{} 0 &{} {0.038} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \end{aligned}$$

(32)

$$\begin{aligned} \mathbb {C}_{b_{5} }^{\prime }= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {0.452} &{} {0.190} &{} {0.145} &{} 0 &{} 0 &{} 0 \\ {0.190} &{} {0.291} &{} {0.101} &{} 0 &{} 0 &{} 0 \\ {0.145} &{} {0.101} &{} {0.433} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {0.094} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {0.118} &{} 0 \\ 0 &{} {0} &{} 0 &{} 0 &{} 0 &{} {0.106} \\ \end{array} }} \right] \left[ {\text{ GPa }} \right] \nonumber \\ \end{aligned}$$

(33)