Net sediment transport in tidal basins: quantifying the tidal barotropic mechanisms in a unified framework

Abstract

Net sediment transport in tidal basins is a subtle imbalance between large fluxes produced by the flood/ebb alternation. The imbalance arises from several mechanisms of suspended transport. Lag effects and tidal asymmetries are regarded as dominant, but defined in different frames of reference (Lagrangian and Eulerian, respectively). A quantitative ranking of their effectiveness is therefore missing. Furthermore, although wind waves are recognized as crucial for tidal flats’ morphodynamics, a systematic analysis of the interaction with tidal mechanisms has not been carried out so far. We review the tide-induced barotropic mechanisms and discuss the shortcomings of their current classification for numerical process-based models. Hence, we conceive a unified Eulerian framework accounting for wave-induced resuspension. A new methodology is proposed to decompose the sediment fluxes accordingly, which is applicable without needing (semi-) analytical approximations. The approach is tested with a one-dimensional model of the Vlie basin, Wadden Sea (The Netherlands). Results show that lag-driven transport is dominant for the finer fractions (silt and mud). In absence of waves, net sediment fluxes are landward and spatial (advective) lag effects are dominant. In presence of waves, sediment can be exported from the tidal flats and temporal (local) lag effects are dominant. Conversely, sand transport is dominated by the asymmetry of peak ebb/flood velocities. We show that the direction of lag-driven transport can be estimated by the gradient of hydrodynamic energy. In agreement with previous studies, our results support the conceptualization of tidal flats’ equilibrium as a simplified balance between tidal mechanisms and wave resuspension.

1 Introduction

Tidal basins are threatened worldwide by accelerated sea-level rise and anthropogenic interferences (e.g., damming and dredging). A major concern is the progressive erosion and drowning of intertidal flats, which provide fundamental ecosystem services (Costanza et al. 1997). It is still questionable whether sediment import is sufficient for the tidal flats to keep pace with accelerated sea level rise (Siefert 1990). In order to examine whether the sediment import suffices, we need to identify and quantify the mechanisms leading to import and export of sediment.

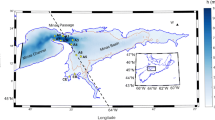
In this paper, we consider the Dutch part of the Wadden Sea (Fig. 1), UNESCO World Heritage since 2009. This area has been heavily impacted over the last century. A closure dam (Afsluitdijk) was built in the 1930s, impounding a wide embayment formerly known as the Zuiderzee. The Afsluitdijk induced major changes in the tidal propagation (Elias et al. 2003). In order to restore its dynamic equilibrium, the westernmost part of the system is still responding by importing suspended matter through the inlets (Elias et al. 2012). Since 1990, the sandy foreshores of the barrier islands are maintained with regular nourishments (Wang et al. 2012). Approach channels are deepened or re-oriented to maintain the access to harbors in the mainland. The import and export mechanisms determine how these human interferences affect the morphological system.

Fig. 1

Western Dutch Wadden Sea. The color bar represents the bathymetry for the year 2011. The bed-level reference is the Normal Amsterdam Peil (NAP). The sub-basins are identified by the watersheds (black contours): (1) Marsdiep; (2) Eierlandse Gat; (3) Vlie (modeled in this study). The Afsluitdijk can be identified by looking at the rectilinear part of the external black contour

Despite a pronounced concentration gradient between the turbid waters of the Wadden Sea and the relatively clear waters of the outer North Sea, sediment is imported from the inlet to the channels and from the channels to the tidal flats (Postma 1954). The hyper-turbid Ems estuary in the Eastern Dutch Wadden Sea is an extreme example of this phenomenon (Talke et al. 2009). Suppression of seaward dispersion is explained by several mechanisms of suspended sediment transport induced by the hydrodynamics.

Tidal flow results in large gross fluxes of sediment entering and leaving the basin. The net fluxes are generally at least an order of magnitude smaller. Given the intrinsic uncertainties in estimating sediment transport rates (whether by modeling or by measurements), the error committed on the gross fluxes can be as large as the total net flux. Improving our understanding of the mechanisms underlying the residual sediment transport is therefore needed, specifically for the Wadden Sea (Wang et al. 2012).

Two categories of sediment transport mechanisms can be defined: baroclinic and barotropic. Regarding the Wadden Sea, there are indications that density-driven currents may play a role (Burchard et al. 2008), but the influence seems to be limited (Becherer et al. 2016). Barotropic mechanisms, arising from asymmetries of the tidal flow in space and time, wind and wave forcing, are considered to be dominant (e.g., Nauw et al. 2014). This is especially the case for basins with marginal freshwater discharges. We therefore focus on the barotropic mechanisms.

Previous studies on identifying the barotropic mechanisms focused on tidal forcing and used either the Eulerian or the Lagrangian frame of reference (FOR henceforward). Van Straaten and Kuenen (1957) and Postma (1961) were the first to show the import of sediment brought about by lag effects in a Lagrangian FOR. Further enhancements of this approach were made by, e.g., Pritchard and Hogg (2003), Pritchard (2005), and Bartholdy (2000). On the other hand, the Eulerian FOR has been used to quantify net sediment transport by tidal asymmetries (e.g., Dronkers 1986; Van de Kreeke and Robaczewska 1993; Wang et al. 1999; Chu et al. 2015). Different frames of reference make it difficult to quantitatively compare the various mechanisms. This can lead to confusion within the literature about the relative importance of the mechanisms.

Sediment transport processes are not determined by only tidal flow. Wind and wave forcing influence the sediment transport patterns in the basin (Le Hir et al. 2000; Lettmann et al. 2009; Sassi et al. 2015). In this paper, we direct our attention to the erosion of sediment by small-amplitiude waves, which has been recognized as a process of major importance for morphodynamics of tidal flats (Green and Coco 2007; Green 2011; Green and Coco (2014; Talke and Stacey 2008; Friedrichs 2012). The wave-orbital velocities influence the distribution of the bed-shear stresses and hence the sediment fluxes caused by the tidal flow. The influence of wave resuspension on direction and magnitude of the tide-induced mechanisms has not been systematically analyzed in previous studies.

In this paper, we aim to (i) build up a conceptual framework that overcomes the current dichotomies regarding definition, classification, and description of the tidal mechanisms; (ii) propose a methodology to quantify these mechanisms, which can be applied to numerical process-based models; (iii) assess the spatial variations of the mechanisms; and (iv) investigate the influence of wave-induced bed shear stresses on the balance of these mechanisms. In order to comply with numerical packages like Delft3D, GETM, ROMS, we adopt the Eulerian FOR. A methodology to identify all mechanisms is therefore needed. This includes a reformulation of the Lagrangian mechanisms in an Eulerian FOR.

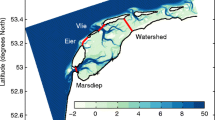
The paper is structured as follows. In Section 2, we first introduce the Lagrangian and Eulerian FOR and formulate the equations for depth-averaged suspended sediment transport in the Eulerian FOR (2.1). Then, we review the mechanisms of net transport as classified in the literature (Sections 2.2 and 2.3). A discussion follows, highlighting the shortcomings in describing and quantifying the mechanisms in a unified Eulerian FOR with the current classification (2.4). Hence, a different classification is proposed along with a methodology to decompose the fluxes accordingly (Section 2.5). This methodology is tested in Section 3 with a model application. The Western Wadden Sea can be divided into various sub-basins (Wang et al. 2011), according to their morphological or hydraulic watersheds (Fig. 1). We consider the Vlie sub-basin, which has a minor fresh water inflow. A 1DH model for tidal flow, wind waves, and sediment transport is introduced and applied for scenarios that are either purely tidal or include wave-induced bed-shear stresses. In Section 4, we discuss the consistency between our conceptual framework and methodology (Sections 4.1 and 4.2), the agreement with previous studies (Section 4.3), and the possible implications of our results for the morphodynamics of tidal basins (Section 4.4). The conclusions are drawn in Section 5.

2 Barotropic mechanisms of residual transport

Tidal mechanisms of residual sediment transport have been described in either the Lagrangian or the Eulerian FOR. Such dualism can lead to confusion in naming and defining the different mechanisms. Mixing the frames of references also complicates a quantitative comparison of the effectiveness of the various mechanisms in driving residual sediment transport. We aim to define a unifying Eulerian FOR that is easy to understand and a methodology to decompose the mechanisms which can be used with the models commonly adopted for coastal studies. These models are process based, fully numerical (i.e., without approximations needed to derive (semi) analytical solutions), Eulerian and most often used in depth-averaged mode.

We limit the definition of the Lagrangian FOR (Section 2.1) and the review of the Lagrangian mechanisms (Section 2.2) to a conceptual level. The mathematical description of the Lagrangian approach is not elaborated. In line with previous reviews (e.g., Friedrichs 2012), the purpose is to qualitatively elucidate the Langrangian mechanisms, in order to identify them in an Eulerian approach. Assumptions and methodologies needed to quantify the mechanisms in the Lagrangian FOR, and why those are not suited for the models mentioned above, are discussed in Section 2.4. Conversely, the definition of the Eulerian FOR (Section 2.1) and the review of the “Eulerian” mechanisms (Section 2.3) are supported by the equations that will be later used in our model application.

However, we confine our attention to the mechanisms that can be captured with a depth-averaged approach. Possible effects arising from the vertical profiles of the variables of interest are not discussed. The limitations of the depth-averaged approach for suspended transport are discussed by, e.g., Toffolon and Vignoli (2007). Additional transport mechanisms can also arise from sub-grid scale processes (e.g., transport around ripples, effects due to coherent turbulent structures; see, e.g., Best 2005).

2.1 Frames of reference and equations for suspended sediment transport

In the real world, sediment particles can be entrained from the seabed, move in three-dimensional water mass and then be deposited onto the bed again. The trajectory of each particle depends on its weight, its shape, and the drag and lift forces applied at each instant by the water motion. Those forces depend on the properties of small-scale turbulence, so that the particle trajectories are chaotic (Fig. 2a). In a model, a frame of reference has to be chosen in order to represent a schematized reality. For the sake of simplicity, our review will always discuss sediment transport along an ideal streamline, so that only 2 directions are possible, i.e., landward or seaward.

Fig. 2

Schematic representations of suspended sediment transport. a Chaotic trajectories of the particles in the real world. b Trajectory of a representative particle in the Lagrangian framework. The frame of reference moves with the particle. c Sediment flux in the Eulerian framework. The frame of reference is fixed in time

In the Lagrangian FOR, we assume that the trajectories of a finite number of particles, often just one, can represent a mean direction of the sediment transport. The frame of reference moves with the particle (Fig. 2b). The trajectory is defined according to threshold velocities (bed-shear stresses) for erosion (U _e or τ _e ) and deposition (U _d or τ _d ). The particle starts on the bed at the beginning of the flood tide (U < U _e ); it is then picked up from the bed (U ≥ U _e ) and horizontally transported landward by the current; it starts settling (U ≤ U _d  ≤ U _e ) while still traveling with the water motion, until it reaches the bed again. The same sequence of entrainment, transport, and deposition happens in seaward direction during ebb tide. At the end of the tidal cycle, the direction of residual transport is defined according to whether the particle is displaced landward or seaward with respect to its initial position.

In the Eulerian FOR, we focus on a specific location in space. The reference is fixed in time. Instead of looking at single particles, a concentration field is considered, whose properties are observed for a control volume as a function of time. The instantaneous suspended transport rate through a cross section is expressed as a mass flux (Fig. 2c), given by the sum of advective and dispersive components, i.e.,

$$ S(t)= QC-\varepsilon bh\frac{\partial C}{\partial x} $$

(1)

where Q = water discharge [m³/s], C = depth-averaged concentration [kg/m³], ε = dispersion coefficient [m²/s], b = channel width [m], h = water depth [m], and x = streamwise coordinate [m]. The direction of residual transport is defined according to the direction taken by the average of S(t) over the tidal period,

$$ {S}_{res}=\frac{1}{T}{\int}_TS(t) dt $$

(2)

with T = tidal period [s] and t = time. The instantaneous depth-averaged concentration is computed via the advection-diffusion equation, which in 1D conservative form reads

$$ b\frac{\partial (hC)}{\partial t}+\frac{\partial (QC)}{\partial x}-\frac{\partial }{\partial x}\left(\varepsilon bh\frac{\partial C}{\partial x}\right)= bh\frac{C_{eq}-C}{T_a} $$

(3)

The right-hand side of Eq. 3 expresses the exchange of sediment between the bed and the water column. This term is typically modeled as a relaxation process, in which the concentration adapts towards its equilibrium value (C _eq ) over a timescale T _a . In our model, this timescale is based on the work of Galappatti and Vreugdenhil (1985) and it is the Eulerian proxy for part of the lag effects (discussed in Section 2.4), reading

$$ {T}_a=\frac{h}{w_s}T=\frac{h}{w_s}\exp \left[\begin{array}{l}\left(1.547\hbox{-} 20.12{u}_r\right){\mathrm{w}}_{\ast}^3+\left(326.832{u}_r^{2.2047}-0.2\right){\mathrm{w}}_{\ast}^2\hfill \\ {}+\left(0.1385\ln \left({u}_r\right)-6.4061\right){w}_{\ast }+\left(0.5467{u}_r+2.1963\right)\hfill \end{array}\right] $$

(4)

with w _s  = settling velocity, u _r  = u _∗/U, w _∗ = w _s /u _∗, u _*  = shear velocity.

The equilibrium concentration C _eq is defined as the depth-averaged concentration resulting from the balance between erosion and deposition fluxes. C _eq is usually calculated by depth-averaging the Rouse profile. The Rouse profile needs a near-bed reference concentration (C _a ) as a boundary condition. Deterministic formulas for C _a need to define a reference height a (e.g., Van Rijn 1993). However, according to Van Rijn (1993), a = 1–10∙D ₅₀ (D ₅₀  = median grain diameter) and small errors in evaluating a can lead to large errors in the profile. Therefore, we can less restrictively define C _eq by modeling the water-bed exchange as

$$ h\frac{C_{eq}-C}{T_a}=E-D=\max \left\{\mathrm{M}{\left(\frac{\tau_{tot}-{\tau}_e}{\tau_e}\right)}^n,0\right\}-\alpha {\mathrm{w}}_s\kern0em C $$

(5)

where E and D are erosion and deposition fluxes, τ _tot τ _tot  = total bed-shear stress (flow and/or waves), τ _cr = critical bed-shear stress for erosion, M = erosion constant, n = 1 erosion exponent, α = C _a /C = 1/T. The relaxation process is now expressed by αα, which is essentially a shape parameter of the concentration profile. The equilibrium concentration stems from

$$ E-D=0\to {C}_{eq}=\frac{E}{\alpha {w}_s} $$

(6)

It is questionable whether the assumptions required to establish a Rouse profile (steady state, parabolic or parabolic-linear eddy diffusivity) hold in case of tidal flow and wave forcing. In particular, horizontal fluxes are not small compared to vertical ones. Our definition of equilibrium concentration is not susceptible to those assumptions, as it only requires the net water-bed exchange to be zero. In fact, the Rouse profile is only a particular solution of the family of solutions satisfying Eq. 6, as α = 1/T can take any value according to Eq. 4.

Note that the right-hand side of Eq. 5 corresponds to the Krone-Partheniades (1962) formulation for cohesive sediment. We however assume continuous deposition throughout the tidal cycle, i.e., the deposition threshold τ _d is removed. Motivations and consequences of removing τ _d are discussed in Section 2.4.1 .

Equation 5 can be readily extended to sand fractions by increasing the erosion exponent to n = 1.5. A number of sand-pickup functions (e.g., Fernandez 1974) can be rewritten in the general form of E. Another advantage of our formulation is that the suspended transport rate linearly scales with M. Therefore, when the focus is on the relative magnitude of the different mechanisms and not on the absolute mass of sediment moving in the real basin, no calibration is needed for the advection-diffusion equation. The erosion constant can be set to a value resulting in reasonable concentrations (e.g., M = 10 ⁻⁵ kg/(m ² s) adopted in our model for all fractions, Section 3).

The choice of the diffusion coefficient (Eq. 3) depends on the considered timescale. Horizontal diffusion is often neglected in studies considering the semidiurnal timescale (e.g., Pritchard 2005; Roberts et al. 2000; Cheng and Wilson 2008), but we retain it in order to aggregate all dispersive processes in a one-dimensional schematization. However, model results (Section 3) confirm that horizontal diffusion is negligible. In our model, a value ε = 100 m ² /s is adopted following Schuttelaars and de Swart (1996).

2.2 Description of the Lagrangian mechanisms: the lag effects

From the pioneering studies of the 1950s onwards (Postma 1954; Van Straaten and Kuenen 1957), a number of mechanisms have been identified in the Lagrangian FOR (see summary in Table 1). Lag effects cause asymmetries of the sediment particle’s trajectory under a periodically reversing flow. Such asymmetries classically result in landward displacement of sediment over the tidal cycle.

Table 1 Overview of the barotropic mechanisms of residual sediment transport under consideration, according to the former classification (Eulerian/Lagrangian) and to the new, fully Eulerian one (Local/Spatial)

Similarly to Van Straaten and Kuenen (1957), we assume a standing tidal wave, so that the water elevation curve is the same for all cross-sections. The flow velocity is uniform over the vertical, so that the sediment particle does not experience variations in horizontal velocity while sinking through the water column. Furthermore, we start by imposing coincident thresholds (U _d  = U _e ) and no time lag between the moment the sediment is picked up and the moment it is lifted up in the water column (see entrainment lag, later in this section). The lag effects are identified and discussed below in more detail.

2.2.1 Settling lag

This mechanism is based on the coupling of non-vertical settling trajectories with the time lag between the instant a particle starts sinking and the instant it touches the bed. The conceptual treatment of Pritchard and Hogg (2003) is reanalysed and extended with the help of Fig. 3. Consider a spatially uniform, sinusoidal velocity in a channel with uniform bed level: a sediment particle is on the bottom at location A (Fig. 3a). During flood, this grain is entrained by a water parcel whose velocity exceeds U _e at that location. The particle follows the trajectory of the water parcel, until the velocity of the water parcel drops below U _d  = U _e . The grain starts settling, but it is horizontally transported farther before hitting the bed. When the flow reverses, the water parcel that formerly carried the sediment is not moving fast enough to re-entrain the particle. Thus, the sediment particle is picked up by a water parcel originating from further landward. Since hydrodynamic conditions are uniform, the particle’s ebb trajectory mirrors the flood trajectory and no displacement occurs over the tidal period. However, tidal basins typically feature a reduction in magnitude of flow velocities with landward distance from the inlet. If we still consider a sinusoidal velocity for each cross-section, but also a landward damping of amplitudes (Fig. 3b), the re-entrainment at ebb tide is caused by a water parcel whose velocity drops below U _d earlier in time with respect to the previous situation. The ebb trajectory is shorter than the flood trajectory and the particle undergoes a net landward shift.

Fig. 3

Settling lag (panels a to d) and scour lag (e) mechanisms. Redrawn and extended after Pritchard and Hogg (2003). The x-axis represents the streamwise distance from the inlet, the y-axis represents the velocity of the sediment (water) particle. The dotted lines are the threshold velocities for erosion and deposition. A different sub-mechanism is illustrated in each panel

According to Van Straaten and Kuenen (1957), the same result is produced by a landward shoaling bed (also a common feature among tidal basins). A drawback of this conceptual model is that the height at which the particle rises in the water column cannot be defined. If we assume such height to be a constant proportion of the water column (e.g., 50%), the lag results in seaward displacement if the particle has to travel over a smaller vertical distance during ebb than during flood. Conversely, a sufficiently steep slope causes the sediment not to settle at all before the next flood, promoting landward residual transport instead (Fig. 3c). In addition to previous studies, we highlight that also in presence of a flat bed, the water-depth variation should play a role. In reality, the tidal wave is never a purely standing wave. The deposition threshold U _d is then attained at a lower water depth during ebb than during flood. In order to touch the bed, the particle has to cover less vertical distance during ebb than during flood (Fig. 3d). On the other hand, real local flow conditions will change the height of the particle in the water column.

Concluding, we have identified three generally coexisting sub-mechanisms contributing to settling lag: velocity damping, bed-level variation and water-depth variation. Without further hypotheses and/or an analytical treatment, the direction of net transport is unequivocally determined only for the first sub-mechanism (the direction of reducing velocity magnitudes, which is typically landward).

2.2.2 Threshold lag

Note that the assumption of a critical velocity (bed-shear stress) for erosion is not a necessary condition for settling lag, but it is needed to pinpoint the start of the particle trajectory in time. The instant of pickup from the bed can alternatively be determined with a probabilistic approach (e.g., Van Prooijen and Winterwerp 2010). If the erosion threshold is adopted, settling lag is enhanced by a mechanism called threshold lag. After each tidal cycle, the sediment particle undergoes a progressive landward displacement. Because of the landward damping of flow velocities, the time of re-entrainment at ebb tide (i.e., when the velocity of the driving water parcel reaches the erosion threshold) will be progressively delayed. When the displacement due to settling lag reaches the innermost regions of the basin, the local flow velocity might be always too low to resuspend the particle again; this condition was originally identified by Van Straaten and Kuenen (1957) as final settling lag.

2.2.3 Scour lag

Similarly to the previous section, the deposition threshold is also needed to pinpoint the instant the particle starts settling. If we introduce the condition U _e  > U _d (previously ignored), settling lag is further enhanced by scour lag. This mechanism consists in a time delay in the re-entrainment of the sediment particle around the moment of flow reversal. In order to reach the erosion threshold during ebb, the mobilizing water parcel must now come from a location even more landward than in case of U _e  = U _d . The subsequent drop of the parcel’s velocity below the deposition threshold is further anticipated in time (Fig. 3e).

2.2.4 Entrainment lag

This mechanism consists of the time taken for the particle to cross the bed-load layer and be lifted up in the water column after it has been picked up from the bed (Nichols 1986). During this time, the movement will be dominated by the flows in the near-bed layer, rather than the depth mean or the flows higher up (Dyer 1997). The time to entrain sediment particles into the water column can be estimated by the mixing time scale: ${T}_{mix}=\frac{h^2}{\varepsilon }$, with an estimate of ε = 0.1hu _∗, we get ${T}_{mix}=\frac{10h}{u_{\ast }}$. For comparison, the settling time scale can be estimated by ${T}_{set}=\frac{h}{w_s}$. The entrainment lag is therefore of the same time scale as the settling lag when u _∗ = 10w _s . Based on this simple scaling analysis, entrainment lag can be as important as settling lag. Only for (very) small particles, the settling lag will dominate over entrainment lag.

2.3 Description of the “Eulerian” mechanisms

The distortion of the tidal signal from a symmetric sinusoid has been historically recognized as a major driver of residual transport in estuaries and tidal basins. Tidal asymmetries are especially due to shallow-water overtides (Dronkers 1986; Friedrichs and Aubrey 1988; Ridderinkhof 1988; Le Hir et al. 2000). The impact on sediment transport is stronger for shallow seas like the North Sea (semidiurnal regime), since a significant M4 component is already present at the inlet. Preliminary analyses conducted with the same model adopted in this paper (Gatto et al. 2015) show that the magnitude of residual transport consistently lowers if solely a M2 constituent is imposed at the open boundary. Tidal asymmetries can also be generated by astronomical interactions among the M2, K1 and O1 constituents (Hoitink 2003; Nidzieko 2010; however, those are relevant only for diurnal or mixed diurnal/semi-diurnal regimes) or by stratification (“internal tidal asymmetry”; Jay 1991). Tidal asymmetries can be divided into 3 sub-mechanisms:

2.3.1 Peak-velocity asymmetry

A difference between maximum ebb velocity and maximum flood velocity induces an asymmetry in sediment transport. The residual transport takes the direction of the highest peak velocity. This mechanism has been mainly investigated for bed-load transport (Van de Kreeke and Robaczewska 1993), which is proportional to a power law of flow velocity with exponent 3–5. However, also in case of suspended transport, the concentration is proportional to the erosion flux, which is proportional to the squared velocity via the bed shear stress. Therefore, according to Eqs. 1 and 5, S(t) ∝ U ³ for cohesive fractions and S(t) ∝ U ⁴ for non-cohesive fractions.

2.3.2 Acceleration/deceleration asymmetry

This mechanism has also been referred to as slack-water asymmetry. A longer slack after high water than after low water implies that sediment will have more time to settle at the end of flood than at the end of ebb. However, the removal of the deposition threshold implies that, although most deposition likely occurs during slack water, the asymmetry results from the full flow acceleration/deceleration phases of the tidal flow. The concentration needs to adapt continuously to the equilibrium value. The larger the acceleration/deceleration is, the larger the difference between the actual concentration and the equilibrium concentration. A difference in the acceleration period (maximum ebb velocity to maximum flood velocity) and the deceleration period (maximum flood velocity to maximum ebb velocity) will subsequently lead to a net sediment transport. This mechanism has been originally described by Groen (1967) in opposition to the arguments of Van Straaten and Kuenen (1957). The apparent disagreement between these two studies is examined and resolved in Section 2.4.

2.3.3 Residual seaward velocity

If the tide propagates into the basin as a partly progressive wave (i.e., water levels and flow velocities are not exactly 90° out of phase), mass is transported landward. The resulting pressure gradient produces a seaward, tidal-mean current that guarantees mass conservation. This process is analogous to the undertow arising from the Stokes’ drift of short waves. In narrow and long estuaries, the magnitude of the current induced by the compensation to the tidal Stokes’ drift can exceed that of river discharge by one order of magnitude (Pritchard 1958). In basins whose diameter is much shorter than the tidal wavelength, the tidal wave is rather close to a standing wave, but the mechanism can still play a role. Furthermore, the net seaward velocity can also arise from width convergence, e.g., when an extensive intertidal area is dewatered through a relatively narrow channel (as in our model, Section 3), or from a river discharge. The residual seaward velocity affects the peak-velocity asymmetry with a vertical shift of the tidal velocity curve.

2.3.4 Wave resuspension

The propagation of waves from the outer sea is restrained by the geometry and morphology of semi-enclosed basins. Talke and Stacey (2003) showed that ocean swells can be a significant source of energy even on the inner tidal flats of the San Francisco Bay. However, most waves in tidal basins are locally generated. Wave growth is limited by both shallow depths and the fetch length, which varies during the tidal cycle due to emerging shoals. Nevertheless, even during fair weather, the enhancement of bed-shear stresses by small-amplitude waves is crucial for the sediment dynamics of shallow channels and tidal flats (Green 2011). There, tidal velocities may be insufficient to exceed the threshold of motion (Talke and Stacey 2008). Conversely, small wave-orbital velocities are ineffective in relatively deep, subtidal areas, where they cannot reach out to the bed.

Conceptually, the dynamic (near-) equilibrium of tidal flats in mesotidal systems is often regarded as a balance between tidal currents causing accretion and wave forcing causing erosion. For example, this is the main theory explaining the lowering of the tidal flats in the Eastern Scheldt since the construction of a storm-surge barrier blocked the sediment supply from the North Sea and reduced tidal ranges and velocities (Eelkema 2013). An idealized study of Hunt et al. (2015) showed tidal flats cannot attain equilibrium without wave activity. In the model of Waeles et al. (2004), constant waves of only 5 cm are capable of causing an export of sediment that is balanced by an input at the seaward boundary. A similar balance is found by Ridderinkhof (1998), who assumes that waves are responsible only for sediment erosion and stirring, while tidal flow determines magnitude and direction of net transport.

However, wave forcing has never been systematically framed with respect to its feedback on the tidal mechanisms we have reviewed. Tidal asymmetries and lag effects are classically regarded as drivers of sediment import from the channels to the tidal flats, but it is unclear whether that still holds if the influence of wave forcing is considered. As an example, Green and Coco (2014) reported about studies in which waves are argued to enhance settling lag by lengthening the settling trajectories, or conversely to impair settling lag by agitating the water column and preventing settling. By means of defining a unifying framework (next Section 2.4), we will be able to assess how wave resuspension affects magnitude and direction of the tidal barotropic mechanisms. In doing so, we adopt the same assumption of Ridderinkhof (1998). Therefore, we neglect wave-driven flows and wave-current interactions, which can be of importance in determining net sediment transport (e.g., Lettmann et al. 2009). In this paper, the focus is set on how the patterns of tide-induced bed-shear stress are altered by the wave-induced component.

2.4 The need for a unifying Eulerian framework

In this section, we discuss shortcomings (Section 2.4.1) and limitations (Section 2.4.2) in pursuing a quantification of the mechanisms in the way they are defined in the review. These problems and limitations are a consequence of an incomplete representation of reality. Consequently, we highlight (Section 2.4.3) and resolve (Section 2.4.4) the disagreements found in the literature regarding definitions and descriptions of the mechanisms. This discussion introduces the baseline concepts which are needed and used to comprehensively redefine all the mechanisms in the Eulerian FOR in the next section (Section 2.5).

2.4.1 Shortcomings of assumptions in Lagrangian models

A major issue arises from the intrinsically stochastic character pertaining to the movement of sediment particles in a flow field. When we model sediment transport with a set of deterministic equations and formulas, we adopt (necessary) assumptions that can be debatable and/or not fully proven in the physical world. Therefore, the assumptions can actually determine the simulated physical response, rather than such response producing insights into the physics. A threshold for deposition is needed for a Lagrangian single-particle approach. Implementing such a threshold in an Eulerian FOR however leads to complications. Adopting a deposition threshold in an Eulerian FOR leads to three mutually-exclusive bed states: degradation (τ _tot  > τ _e ), stable (τ _d  < τ _tot  < τ _e ) and accretion (τ _tot  < τ _d ). An equilibrium concentration as defined in Eq. (6) cannot be defined anymore, since erosion and deposition do not occur at the same time. For a degrading bed, the concentration increases, while the concentration decreases for accreting beds. Such a representation is not physically sound, as indicated by Winterwerp et al. (2012). A continuous deposition flux is therefore proposed. Neglecting the deposition threshold however implies that the scour lag mechanism (Section 2.2.3) simply cannot exist in an Eulerian FOR. In Section 2.3.2, we already discussed the unsuitability of the name “slack-water asymmetry” when removing the assumption of the threshold bed-shear stress for deposition.

Threshold lag (Section 2.2.2) is similarly canceled out if the erosion threshold τ _e is omitted. It is not uncommon to assume that C _eq or the transport rates vary as a power of the flow velocity, without a critical value for the initiation of sediment motion (e.g., Engelund and Hansen 1967). Conversely, a new resuspension lag mechanism is created in the particle-tracking approach of Bartholdy (2000). That approach assumes a single, representative sediment particle which starts settling when the first half of the total material deposited during flood has reached the bed. The second half of material deposits on top of the representative particle. During ebb, this volume of sediment has to be fully eroded before the representative particle can be exposed to the flow and resuspended again. This “burial effect” is in practice similar to scour lag, i.e. it induces a time delay in the re-entrainment of the particle around the moment of flow reversal.

2.4.2 Limitations of applications in Lagrangian models

The application of single-particle (Lagrangian) models is limited. Dispersive processes cannot be included. More erosion during high flow velocities and more deposition during long slack waters cannot be dealt with, unless the mass per particle is not constant or a large number of particles is considered. However, the pickup of individual particles from the bed is a stochastic process and it should be modeled as such. Deposition depends on the processes in the near-bed layer, where the scales of turbulence are involved. Therefore, erosion and deposition thresholds are poor parameterizations for the particle trajectory. In the qualitative review of the Lagrangian mechanisms (Section 2.2), the height at which the particle rises in the water column is not defined, but that is needed for a model application. The particle lift is related to turbulence and vertical flow velocity (e.g., Bartholdy, 2000). Therefore, depth-averaged models cannot be used. A proper parameterization for the trajectories of sediment particles is far from straightforward and further complicated if we want to include the orbital motions of short waves. Moreover, a morphodynamic model needs also the Eulerian FOR in order to update the bed level. Eventually, a three-dimensional, process-based model with particle tracking at the basin scale is most likely unfeasible for its computational effort.

Therefore, the lag effects are typically investigated with idealized models, adopting geometries that are schematized and/or confined to, e.g., a channel-flat system. Those models generally adopt simplified hydrodynamics in order to construct (semi-) analytical solutions (e.g., Pritchard and Hogg 2003; Schuttelaars and de Swart 1996), especially the pumping flow (rigid lid) solution. If the basin length is much shorter than the tidal wavelength, water levels can be approximated as being spatially uniform at first order. Although this approximation is conceptually reasonable, shortcomings arise. Unrealistically high flow velocities are obtained if adopting a sloping bathymetry with tidal flats undergoing flooding and drying. Currents in intertidal areas become friction dominated. The pumping-flow solution does not include bed friction, so the M6 overtide cannot be generated. This overtide affects the acceleration/deceleration asymmetry (Van de Kreeke and Robaczewska 1993). Furthermore, a purely standing tidal wave cannot produce the tidal Stokes’ drift, unless higher-order corrections are applied to the solution.

2.4.3 Ambiguities with definitions of the mechanisms

Different authors do not always agree upon nomenclature and/or definition of the mechanisms under consideration. Dyer (1997) and Pritchard (2005) both used the term “scour lag” when referring to the mechanisms hereby named “entrainment lag” (Section 2.2.4) and “threshold lag” (2.2.2), respectively. Yu et al. (2011) drew an analogy between settling lag and a “vertical sorting” process causing the variability of phase lags between concentrations and flow velocities along the water column.

Groen (1967) described a mechanism which is different from settling lag, but his paper is written as an opposition to Van Straaten and Kuenen (1957). This might be the reason why authors like Van Leeuwen et al. (2003) and Elias et al. (2006) refer to Groen’s effect as “temporal settling lag.” The disagreement between Groen and Van Straaten & Kuenen arises from the adoption of different frames of reference. Groen adopted an Eulerian analytical model, reading

$$ \frac{\partial {C}_r}{\partial t}=\frac{C_{eq}-{C}_r}{T_a} $$

(7)

$$ {C}_{eq}=\lambda {U}^2 $$

(8)

in which T _a is a constant adaptation time, λ is a constant coefficient and U = depth-averaged flow velocity. Note that henceforth, we define C _r that solves Eq. 7 as time-relaxed equilibrium concentration and C _eq as instantaneous equilibrium concentration. The conservation of sediment mass as expressed by Eq. 7 neglects the advection and diffusion terms. However, according to the definition of settling lag, an Eulerian equivalent shall pertain to both the advection term and to a deposition term. The advection term shall account for the spatial component of settling lag (the particle is transported horizontally), while the deposition term shall account for the local component (the particle sinks through the water column). The distinction between spatial and/or local character of the lag effects is the first key concept necessary to redefine the lag effects into the Eulerian FOR.

2.4.4 Shortcomings with isolation of the mechanisms

The second key concept is that in the Eulerian FOR, we define the lag effects as mechanisms causing a deviation of the instantaneous concentration from C _eq in a control volume. This is the same underlying assumption of Groen (1967), although he did not consider that advection also contributes to such deviation. However, we also start by considering only local processes. If we adopt Groen’s model and neglect the lag effects, then C = C _eq  ∀ t (Eq. 8) and the acceleration/deceleration asymmetry (Section 2.3.2) does not produce net tidally averaged transport (Fig. 4a). Net transport is also zero if we allow the deviation from C _eq (Eq. 7), but the velocity is symmetrical around both axes (Fig. 4b). Therefore, acceleration/deceleration asymmetry and deviation from the instantaneous equilibrium concentration both need to be present in order to produce net suspended transport (Fig. 4c). Differently, the peak-velocity asymmetry (Section 2.3.1) results in net transport also if C = C _eq  ∀ t (Fig. 4d). However, shallow-water overtides do not generate one of those two tidal asymmetries without the other, so that the net transport resulting from Eq. 7 aggregates peak-velocity asymmetry, acceleration/deceleration asymmetry and the local deviation from the instantaneous equilibrium concentration (Fig. 4e).

Fig. 4

Groen’s (1967) model under different combinations of mechanisms. The x-axis represents time (ticks not shown), the left y-axis represents flow velocities (light-blue line) the right y-axis represents the concentration (red line). The areas filled in dark blue represent the integral of the transport rate in time, whose mean is indicated below the x-axes. a Acceleration/deceleration asymmetry (ADA) without lag effects (LE). b Symmetrical velocity with lag effects, no threshold lag. c Acceleration/deceleration asymmetry with lag effects, no threshold lag. d Peak-velocity asymmetry (PVA) without lag effects. e Peak-velocity asymmetry and acceleration/deceleration asymmetry with lag effects, no threshold lag. f All the mechanisms in (e) plus threshold lag (THL). All units are in the SI system

In the Eulerian FOR, it is hardly possible to quantify a single mechanism in isolation from the others. Groen’s model does not take into account a particular lag effect, but rather the local component of all lag effects having a proxy inside the water-bed exchange term of the advection-diffusion equation. In Eq. 7, only a general “bulk” effect is considered (T _a  = const.), which does not vary with the flow conditions and does not explicitly pertain to an erosion or deposition term. If we prescribe that C _eq  = 0 when U ≤ U _e in Eq. 8, we introduce a proxy for threshold lag. Threshold lag (Section 2.2.2) is an exception to our definition of the lag effects in the Eulerian FOR, as it does not cause C to deviate from C _eq . However, when combined to the situation in Fig. 4d (only peak-velocity asymmetry) and/or to the situation in Fig. 4c (acceleration/deceleration asymmetry plus other lag effects), threshold lag affects the magnitude of net transport (compare Fig. 4f to e).

As a further example of problems in isolating the mechanisms, suppose we want to model (either with a Lagrangian or an Eulerian approach) a scenario in which settling lag is the only acting mechanism. That would require two conditions: (i) other lag effects are not present or neglected; (ii) the amplitude of the tidal-velocity curve dampens landward while keeping symmetrical around both axes. As explained by Pritchard (2005), the second condition would require the external forcing to be non-harmonic. In fact, the interaction between tidal forcing and bathymetry always generates the acceleration/deceleration asymmetry inside the basin, even if the external tidal forcing is symmetrical and water levels are approximated with the pumping flow solution.

2.5 Aggregating the mechanisms in the Eulerian frame of reference

The discussion in the previous section highlights that it is not possible to pursue a quantification of the mechanisms in isolation, as those have been defined in our review. The requirements for such quantification are not applicable to the models most commonly adopted for coastal morphodynamics (process-based, numerical, Eulerian, depth-averaged). Somewhat crude assumptions are needed either for the sediment dynamics (e.g., the representative particle) or the hydrodynamics (e.g., the pumping flow solution).

Hence, we propose a reductionist approach based on the aggregation of the mechanisms into three categories. We assume that the total residual transport (Eq. 2) through a cross-section can be linearly decomposed as

$$ {S}_{res}={S}_{VA}+{S}_{TL}+{S}_{SL}+{S}_{dis} $$

(9)

in which the first three subscripts on the right-hand side stand for velocity asymmetry (VA), temporal lag (TL), and spatial lag (SL), respectively, and ${S}_{dis}=\frac{1}{T}{\int}_T-\varepsilon bh\frac{\partial C}{\partial x} dt$ is the net dispersive flux.

With velocity asymmetry, we aggregate the peak-velocity asymmetry and the residual seaward velocity (Sections 2.3.1 and 2.3.3). The residual flux due to the velocity asymmetry is the tidally-averaged transport that would be present if the concentration could instantaneously adapt to C _eq , viz.

$$ {S}_{VA}=\frac{1}{T}{\int}_TQ\cdot {C}_{eq} dt $$

(10)

We define temporal lag as the combination of the acceleration/deceleration asymmetry (Section 2.3.2) and the local components of the lag effects. In order to compute the flux of temporal lag, we adapt Groen’s model (Eq. 7) to our set of equations for suspended transport (Section 2.1)

$$ \frac{\partial \left({hC}_r\right)}{\partial t}=E-D=\max \left\{\mathrm{M}{\left(\frac{\tau_{tot}-{\tau}_e}{\tau_e}\right)}^n,0\right\}-\alpha {w}_s{C}_r $$

(11)

Differently from Groen’s model, our adaptation time T _a (contained in α = h/(w _s T _a )) is not constant nor uniform (Eq. 4) and it explicitly pertains to the deposition term. The entrainment lag (Section 2.2.4) can also be interpreted as a consequence of the adaptation to the new equilibrium concentration. The adaptation time T _a contains both timescales of settling and entrainment, hence it is a proxy for the local settling lag and entrainment lag. The proxy for threshold lag (τ _e ) is in the erosion term.

As discussed in Section 2.4.4 and showed in Fig. 4e, the residual flux computed by imposing C = C _r includes both velocity asymmetry and temporal lag. Therefore, the residual flux due to temporal lag is

$$ {S}_{TL}=\frac{1}{T}{\int}_tQ\cdot {C}_r dt-{S}_{VA} $$

(12)

In other words, we assume that C _r  = C _eq  + C′, C′ being the deviation from C _eq due to temporal lag. Additionally, for a given control volume, the deviation of C from C _eq also depends on the amount of sediment advected from the neighboring control volumes. In turn, this amount depends on the flow variability in space (e.g., landward damping of velocities) and on the lag effects. In comparison to a “no-lag” situation, settling lag increases advection by delaying deposition in the neighboring control volumes, while threshold lag decreases advection by limiting erosion in those volumes. We define spatial lag as the aggregation of flow gradients and spatial components of the lag effects. The net flux due to spatial lag is computed by subtracting the net flux obtained with the reduced sediment mass balance (Eq. 11) from the flux obtained with the complete equation (Eq. 3)

$$ {S}_{SL}={S}_{res}-{S}_{VA}-{S}_{TL}-{S}_{dif} $$

(13)

Building from Friedrichs (2012), spatial lag shall be interpreted as the transport asymmetry arising from the imbalanced, alternating advection between areas at different levels of hydrodynamic energy. In presence of a landward damping of velocities, flood flow transports more sediment landwards than ebb flow transports seawards. Hence, the tidally averaged advection can be interpreted as a dispersive process in which net transport goes from high to low energy areas. This process is an Eulerian analogue of settling lag, as it is based on the same condition (landward damping of flow velocities). Note that here we build upon studies that feature a channel discharging into a flat, so the transport is in longitudinal direction as the main flow component. For a channel with bordering flats, Mariotti and Fagherazzi (2012) depicted a lateral exchange process (the channel spillover mechanism): that configuration also shares the same basic principles of Friedrichs’ generalized concept.

A few notes on this methodology are worth mentioning. S _VA and S _TL are computed by neglecting the instantaneous contributions of spatial lag, which is conceptually different from imposing no net contribution of its tidal average. However, if the latter condition is imposed instead, the time integration of Eq. 3 with the condition ${\int}_T\frac{\partial (QC)}{\partial x} dt=0$ still yields C = C _eq as a trivial solution (assuming C periodic and small diffusion). Furthermore, dispersion can have the same effect of spatial lag if a concentration gradient exists within a uniform flow.

Finally, several authors (Galappatti and Vreugdenhil 1985; Armanini and Di Silvio 1988; Wang 1992) considered also a length scale of relaxation (adaptation length) for the sediment concentration. The adaptation length is a coefficient in front of the advection term of the sediment continuity equation, and it can be regarded as a proxy for the spatial component of the lag effects. Our sediment continuity equation (Eq. 3) is similar to the one adopted by the software package Delft3D. It uses a judicious simplification of the asymptotic solution of Galappatti and Vreugdenhil (1985), in which the adaptation length gets absorbed in the equation.

In conclusion, we have substituted a classification based on the kinematics of the single mechanism with a classification based on the character of the result (local/spatial) of all acting mechanisms (Table 1). De Swart and Zimmerman (2009) provided an analytical methodology in line with our conceptual framework, i.e., they distinguished a “local settling lag” from a “spatial settling lag.” However, our goal was to propose a methodology that can be applied when a model only allows for numerical solutions. That implies we cannot push the fluxes’ decomposition further without involving higher-order dynamics. Our decomposition neglects all non-linear interactions among the different mechanisms and prevents the possibility of discriminating a particular lag effect from the others. Nevertheless, as proven by our model application (next Section 3), the bulk effect of conceptually coherent mechanisms is retained.

3 Application to the VLIE basin

3.1 Model description

In order to test our methodology, we choose a one-dimensional model. Neglecting multidirectionality allows us to more easily highlight whether the mechanisms produce landward (sediment import) or seaward (export) fluxes. We adopt the hybrid approach of Van Prooijen and Wang (2013), i.e., a process-based model with an idealized geometry. The model is cross-section integrated.

3.1.1 Geometry

The hypsometric curve of the Vlie basin is obtained from the measured bathymetry. A submerged area A _n (z _n ) is determined for the area with a bed level z smaller than z _n , where the index n refers to the volume number. The hypsometric curve is discretized into N = 1000 cells which have a width B _n , length ∆x _n , and area A _n  = b _n ∙∆x _n . The mass balance for each cell reads

$$ An\frac{h_n^i-{h}_n^{i-1}}{\varDelta t}={(Ubh)}_{n-\frac{1}{2}}^i-{(Ubh)}_{n+\frac{1}{2}}^i $$

(14)

with h = water depth, U = depth-averaged flow velocity, ∆t = timestep, i = time index, n = cell index. A staggered grid is used, with the fluxes defined at the faces n ± 1/2. Water depths and flow velocities are obtained from a state-of-the-art hydrodynamic model of the Dutch Wadden Sea (Duran-Matute et al. 2014), which uses the software package GETM (Stips et al. 2004). The cells of the GETM model are ordered by the bed level and related to the volumes as used in the continuity equation. A number of 2D GETM cells are binned per 1D volume. For each timestep of a spring-neap cycle, the mean water depth and velocity per bin are used to solve the continuity equation for b. The width of each 1D volume is then defined by averaging all the “instantaneous” widths of that volume. The length of each volume stems from Δx _n  = A _n /b _n . The geometry is eventually interpolated to N′ = 221 grid cells of constant length ∆x’ = 100 m. The hypsometric curve and the geometry of the 1D basin are presented in Fig. 5. The reader is referred to Van Prooijen and Wang (2013) for an exhaustive explanation of this methodology (the only difference is that median widths are used there) and the discussion about its assumptions and implications. With respect to commonly-adopted schematizations (e.g., rectangular basin, flat or linearly-sloping bottom), our geometry has the advantage of being observations-based albeit schematized. That results in a correct reproduction of the lumped parameters of the basin which are crucial for a realistic hydrodynamics: total surface area and its intertidal/subtidal ratio; basin diameter, influencing the standing/progressive character of the tidal wave; tidal prism, determining the amount of water exchanged with the outer sea.

Fig. 5

a Bird’s-eye view of the schematized basin (note the distorted aspect ratio and compare to Van Straaten and Kuenen 1957)—b) Model’s geometry: hypsometric curve (dashed red line, left and upper axes) and width as a function of the streamwise coordinate (solid black line, right and bottom axes). Yellow dots mark the low-water line under the prescribed tidal forcing. The 1D basin can be considered as the alignment of all the branches belonging to a fractal tidal network. The network gets monotonically shallower by developing from the inlet to the watershed, homogeneously covering the basin area. All tidal flats are at the landward end. The self-similar structure is observed in the channels of the Wadden Sea at sufficiently small scales (Cleveringa and Oost 1999), and especially the Vlie basin resembles this schematization (Fig. 1)

3.1.2 Hydrodynamics

Tidal hydrodynamics are simulated with the package Delft3D (Lesser et al. 2004), using the depth-averaged shallow water equations. The investigated mechanisms act on the semidiurnal tidal timescale. Hence, the external forcing consists in the water elevation modulated by the main constituents for that cycle, i.e., M2 and M4. Seasonal and inter-annual variability of such constituents at the Vlie inlet is only a few percent (Gräwe et al. 2014), giving confidence about the representativeness of a single boundary condition that prescribes the yearly-mean values of amplitudes and phase shifts. Those parameters (Table 2—boundary tide) are obtained from tidal analysis of water elevations recorded every 10 min at the nearby Terschelling-North Sea station, during the years 2009–2010: the methodology proposed by Gräwe et al. (2014) is followed. Consequences of spring/neap variations and a different tidal asymmetry at the open boundary are considered in the discussion.

Table 2 Overview of the essential simulation parameters

Simulated flow velocities are realistically distributed with respect to bed levels. That is crucial in order to correctly reproduce bed-shear-stress gradients and hence sediment-transport patterns. However, as a trade-off, we have to accept an underestimation of the water level magnitude in the intertidal area: the (de)watering of tidal flats is slowed down by the absence of tidal creeks which are present in reality.

Flow velocities and water levels computed by Delft3D are then imported into a Matlab program. Simplified wave forcing is added via the dimensionless approach of Young and Verhagen (1996), as the 1D model has to neglect directionality. In order to highlight the effect of altering the patterns of total bed-shear stress, wave forcing is only taken into account as an enhancement of the flow-induced component of bed-shear stress. No feedback on the hydrodynamics is considered. The calibration of Van Prooijen and Wang (2013) is retained, with a fixed fetch length of 5 km. Extensive data analysis performed and reviewed by Van der Westhuysen and De Waal (2008) suggests a breaking criterion $\gamma =\frac{H_s}{h}\approx 0.35$ (H _s  = significant wave height and h = water depth) for the Wadden Sea. However, both the spectral model SWAN used by these authors and tests of the Young & Verhagen’s formulation conducted by Mariotti and Fagherazzi (2013) show both models tend to systematically underpredict the wave heights on the tidal flats. For our schematized geometry, underprediction of wave heights is also expected as a consequence of underpredicted water levels in the shallowest region. Aiming to compensate for these aspects, a “typical” γ = 0.73 is chosen. Wave heights per grid cell are computed by imposing a constant and uniform wind speed (U ₁₀ ) at + 10 m NAP (Dutch reference datum, ≈ MSL). A large set of simulations is produced by means of increasing U ₁₀ from 0 to 30 m/s by a step of 0.5 m/s (the yearly average is about 7 m/s). The wave-induced and flow-induced components of the total bed-shear stress are summed without accounting for the interactions parameterized by Grant and Madsen (1979).

3.1.3 Sediment transport

Sediment transport is computed with a Matlab program solving the equations presented in Section 2.1. Simulations are run for a variety of cohesive and non-cohesive fractions, among which three representative ones are shown (Table 2—sediments). No interactions among the different fractions are prescribed, neither in the bed nor in the water column. For each simulation, the bed is assumed to consist of 100% of the considered sediment type. For cohesive sediments, a constant settling velocity is imposed and the critical bed-shear stress is set to a common value for slightly consolidated deposits. Processes like flocculation and consolidation are left out. For non-cohesive sediments, grain diameters are set. The settling velocities are computed using the formula of Zhiyao et al. (2008) and the critical bed-shear stresses follow from the Shields’ parameter in the non-cohesive regime (Yalin and Karahan 1979). Mud content in the Vlie basin is hardly above 20% (Van Ledden 2003). This implies that the critical bed-shear stress does not depend on the mud content (Van Rijn 1993).

As the focus is set on the residual sediment transport for short timescales, no morphological module is implemented: bed levels are fixed in time. For the same reason, the time-relaxed equilibrium concentration, as following from Eq. 14, is imposed at the open boundary. We neglect ebb-tidal-delta dynamics in prescribing the external sediment supply to the system. Two main timescales can be identified for the sediment dynamics of tidal basins. This is a basic assumption of, e.g., the semi-empirical model ASMITA (Van Goor et al. 2003). At the relatively “short” timescale, the system internally redistributes its sediment between channels and tidal flats. At the “long” timescale, a sediment demand by tidal flats (channels) being below (above) their equilibrium volume (note this is defined as the volume of water for the channels and the volume of sediment for the flats) will be satisfied with sediment coming from the ebb-tidal delta (if available). The sediment demand can be due to sea-level rise or to a response to human interventions (as described in the introduction). Therefore, assuming an equilibrium concentration at the ebb-tidal delta is reasonable for the purpose of this study, but likely not for long-term morphodynamic simulations.

3.2 Model results

Figure 6 shows the contributions of the three different mechanisms (velocity asymmetry, temporal lag and spatial lag) and horizontal diffusion for the reference scenario (no wave forcing). In order to better display the variation in the results’ magnitude, the basin is split in three transects: deep (z = − 30 to − 5 m), shallow subtidal (z = − 5 to − 1 m) and intertidal (z = − 1 m and higher). Net diffusive fluxes are practically zero (in the order of F _dif  ≈ 10 ⁻¹⁶ kg/s). Temporal lag is also negligible for all positions and all fractions. A small contribution of temporal lag is found in the deepest part only for the mud fraction (Fig. 6, 1a). At that location, the timescale h/w _s is largest and the instantaneous concentration will be farthest from the equilibrium concentration.

Fig. 6

Residual sediment fluxes due to the transport mechanisms under investigation (see legend) in the schematized Vlie basin, as a function of bed levels (black x-axes) and distances from the mouth (blue x-axes). Positive (negative) signs mean sediment leaves the grid cell in landward (seaward) direction. The rows of the plot matrix indicate the sediment type, the columns indicate the transect

In the deep subtidal part, the total sediment flux is the consequence of velocity asymmetry and spatial lag. Velocity asymmetry promotes seaward transport, as flow velocities are ebb-dominant. In the first half of the transect, spatial lag results in seaward net fluxes as velocity magnitudes increase landward. This can be regarded as a model artifact. In reality, the highest velocity should be at the inlet gorge, where the tidal currents are constricted in a tidal jet (Armstrong 1963). The GETM simulation (Duran-Matute et al. 2014) also shows a clear decreasing trend of velocities with distance from the inlet (Fig. 7).

Fig. 7

Peak velocity magnitudes as a function of the normalized distance from the inlet, as modeled in this study (black and red lines) and by the 2D GETM simulation used to derive the model’s geometry (blue dots)

In the second half of the deep subtidal transect, velocity magnitudes start decreasing landward. Therefore, spatial lag results in landward fluxes that can overturn the seaward transport that velocity asymmetry would impose for mud (Fig. 6, panel 1a, z ~ − 13 m) and balance it out for silt (panel 2a), but it is ineffective for sand (panel 3a). The coarser the fraction, the more effective is the ebb-dominant velocity asymmetry.

In the “shallow subtidal” region, spatial lag becomes more effective in causing landward transport against ebb-dominant flow velocities (Fig. 6, panel 1b). However, its magnitude rapidly decays at decreasing water depths, as advection becomes much smaller than local terms in the advection-diffusion equation (Eq. 3). Peak velocities shift into flood-dominant at a bed level of ~ − 2.3 m and so does the velocity asymmetry. While the zero-crossing position of velocity asymmetry does not change per grain size (it is “fixed” by flow velocities), the zero-crossing of the total flux does. Coarsening the grain size reduces the contribution of spatial lag. The zero-crossing moves landward (Fig. 6, 2b) until it coincides with that of velocity asymmetry for fine sand of 150 μm (panel 3b), which is too coarse to experience any lag effect already at these depths.

In the intertidal region, total transport is landward. Spatial lag is dominant for the finest fraction (Fig. 6, panel 1c), while the total net transport of the other two fractions is fully determined by the velocity asymmetry (panels 2c, 3c). The magnitude of the fluxes becomes very small at about z = − 0.3 m. In absence of water-level setup of non-tidal origin, we can argue that transport at shallower water almost fully takes place as bed-load. Moreover, bores produced by wave breaking are not modeled. Finally, the largest overall magnitude of the fluxes is observed for the silt fraction. Mud is more easily transported than sand as its low settling velocity results in more mass kept in suspension throughout the tidal cycle, despite its critical bed-shear stress being 50% higher.

For wave-forcing scenarios, the fluxes are interpolated as surface color plots on a two-dimensional grid, whose axes contain bed level/distance from the inlet and the maximum wave height for the whole transect over the tidal cycle. The results for silt (w _s  = 2 mm/s) are presented in Fig. 8. Net diffusive fluxes are omitted as they do not increase with respect to the tide-only case. The deepest region is omitted, as waves are mostly ineffective there: however, relatively large waves are able to penetrate the bed and spatial lag becomes the dominant mechanism also for the sand fraction. A general trend can be observed with respect to the tide-only case. Increasing wave heights gradually reduce (increase) the magnitude of the total flux where net transport is landward (seaward). Nevertheless, relatively small waves can occasionally also enhance the sediment import (panel 2a, z = −1 m, H _s  < 30 cm). These waves can increase flood transport by prolonging the timespan in which the bed-shear stress is higher than the erosion threshold during flood.

Fig. 8

Residual fluxes of silt (w _s  = 2 mm/s) in presence of wave resuspension. Columns of the plot matrix indicate the mechanisms, rows indicate the transect. Fluxes are plotted as a function of bed levels (black x-axis), distance from the inlet (blue x-axis) and maximum wave height in the transect over the tidal cycle (y-axis). Note the two distinct color bars for the fluxes’ magnitude

Velocity asymmetry is not substantially affected by wave resuspension in the shallow subtidal region, since flow velocities are not changed (the contours are almost vertical in Fig. 8, panel 1b). Conversely, the mechanism is affected in the intertidal region, where wave resuspension increases the equilibrium concentration by significantly increasing the bed-shear stress (Eq. 6). When waves are relatively large, ebb transport can exceed flood transport (Fig. 8, panel 2b) despite the flood-dominant peak-velocity asymmetry (Fig. 7, x > 0.65).

The trends of concentration in time for an intertidal cross-section (z = −0.3 m NAP, Fig. 9) show no sediment in suspension during ebb flow in absence of waves. For larger waves, the concentrations are different for ebb flow versus flood flow. The concentrations during ebb are 2 (3) times larger than during flood for wave heights of ~ 30 cm (~ 45 cm). This enhances the effectiveness of temporal lag, which was negligible in the tide-only case. However, the mechanism promotes net seaward transport, despite the larger acceleration phase compared to the deceleration phase (compare to Fig. 4c of Groen’s model for the tide-only case). In the intertidal area, the tidal wave is almost a purely standing wave. Concentrations are highest during high-water slack, when the flow velocity is zero. That sediment will be afterwards available for the ebb flow to carry if the time-relaxation of concentrations is prescribed (Eqs. 11 and 12). If not (Eq. 10), the instantaneous equilibrium concentration drops at the start of ebb flow, as waves are impaired by decreasing water depths and velocities are low. Compare the reduction in net sediment import, and the quicker transition to export at increasing wind speeds, going from only velocity asymmetry (Fig. 8, panel 2b, z = −0.7 m) to the total flux (panel 2a).

Fig. 9

a Temporal trends of concentrations for wave scenarios generated by varying wind speed (U ₁₀ ), at an intertidal cross section (z = − 0.32 m NAP). b Flow velocity (dotted blue line, left y-axis) and significant wave heights (right y-axes) in time at the same cross section

Spatial lag exhibits an irregular trend in the shallow subtidal region (Fig. 8, panel 1d), where it can result in both landward or seaward fluxes depending on the wave heights and on the depth. In the intertidal region (panel 2d), spatial lag becomes slightly effective only for relatively large waves. In the following discussion (next section), the trends of spatial lag are explained in terms of Friedrichs’ (2012) energetics approach introduced in Section 2.5. Eventually, this thorough sensitivity analysis lets us sketch an impression of the mechanisms’ ranking for different grain sizes, bed levels, and wave heights (Fig. 10).

Fig. 10

Qualitative sketch of the dominant mechanisms of net sediment transport for varying bed-levels (z -shallow/deep), wave-height conditions (H _s - calm/wavy) and grain size (D - fine/coarse). For each scenario: the color of the outer circle represents the leading mechanism (see legend); the size of the outer circle represents the magnitude of total net transport with respect to the other scenarios; the color of the inner circle represents the secondary mechanism; the size of the inner circle represents the magnitude of the secondary mechanism with respect to the leading mechanism in the same scenario. The lines connect scenarios which share 2 out of the 3 determining parameters. When the transition causes (does not cause) the leading mechanism to change, the line is solid (dashed)

4 Discussion

4.1 The concept of “energy-driven” transport

Friedrichs (2012) generalized the concept of net transport due to spatial asymmetries as a “sort of tidal dispersion […] driven by spatial variations in total hydrodynamic energy working in concert with time lags in the relationship between instantaneous bed stress and depth-integrated suspended sediment concentration”. In Section 2.5, we have based our definition of spatial lag on this concept. Here, the concept is quantified.

We adopt the erosion potential (Stanev et al. 2007) as a proxy for the tidally-averaged hydrodynamic energy,

$$ {K}_{\$}=\frac{1}{T}{\int}_T\max \left\{\left(\frac{\tau_{\$}-{\tau}_e}{\tau_e}\right),0\right\} dt $$

(15)

with T = tidal period, τ _e  = critical bed-shear stress for erosion, τ _$  = bed-shear stress and the subscript $ indicating either the total (tot - flow plus waves), the flow-induced (f) or the wave-induced (w) component. The net flux by spatial lag can then be related to the negative gradient $\left(-\frac{dK_{tot}}{dx}\right)$ of the erosion potential. If $-\frac{dK_{tot}}{dx}>0$ energy decreases landward and spatial lag results in net landward transport: if $-\frac{dK_{tot}}{dx}<0$, energy increases landward and spatial lag results in net seaward transport. This is shown in Fig. 11, where the flux of spatial lag and the negative derivative of the erosion potential follow the same pattern.

Fig. 11

Comparison between spatial lag flux of silt (blue and black dashed lines, left y-axis) and erosion potential (right y-axis) in the shallow subtidal and intertidal regions, as a function of the distance from the inlet. Red line: flow plus waves; green line: waves only; magenta line: flow only. In the considered scenario, maximum significant wave heights decrease along the transect from Hs ≈ 90 cm to Hs ≈ 30 cm, with an almost linear trend

In the Lagrangian FOR, settling lag is conceptually regarded as a sediment-importing mechanism, based on the assumptions of no waves and landward decreasing velocities (and hence bed-shear stresses). Conversely, the generalized spatial lag mechanism can also promote export of sediments, since wave forcing alters the distribution of tidally-averaged bed-shear stresses. In Fig. 11, we can observe that also $-\frac{dK_f}{dx}<0$ along a small transect of the shallow subtidal region (12 < x < 14 km), in which flow velocities are increasing landward (see Fig. 7, x ≈ 0.6). However, K _f decreases monotonically landward of that location. Conversely, wave-induced resuspension finds its “optimum” depth in the competition among timespan of exposure (duration of the submerged stage), depth-attenuation of orbital velocities and dissipation/breaking (Green and Coco 2014). In other words, the water column has to be shallow enough for the waves to penetrate to the bed, but not too shallow to prevent high dissipation. The trend of K _w is therefore not monotonic, presenting a local maximum at some intermediate coordinate of the bed-level profile. In comparison to the no-waves case, wave resuspension enhances the net seaward flux of spatial lag for 12 < x < 14 km and reduces the net landward flux for x > 14 km. In the intertidal region (x > 18 km), K _f is practically zero and the landward-increasing energy is fully determined by waves. However, advection by tidal velocities is too small to cause a landward residual flux.

Since the direction of the residual flux by spatial lag follows the gradient of hydrodynamic energy acting on the bed, the bulk effect of a complex mechanism is well caught by a basic concept of physics, viz. dispersion. State-of-the-art, process-based models feature much higher complexity and computational effort than our idealized model. Our quantitative proof of Friedrichs’s (2012) concept implies that preliminary indications about the residual fluxes can be obtained by simply looking at maps of time-averaged bed-shear stresses.

4.2 Methodology vs. conceptual framework

Model results prove the consistency between the conceptual framework and the methodology elaborated in Sections 2.4 and 2.5. The magnitude of lag-driven transport decreases with increasing grain sizes and increasing bed levels. If only tidal flow is considered, the direction of the net flux due to the velocity asymmetry is determined by the direction of the higher peak velocity between flood and ebb, independently of the grain size. However, that is not always the case when wave resuspension is included (Fig. 8, panel 2b, y > 60). In the intertidal region, the peak velocity is strongly flood-dominant and it coincides in time with the peak bed-shear stress. Nevertheless, the ebb-dominant asymmetry of C _eq prevails over the flood-dominant asymmetry of U (Eq. 10), determining a net seaward flux.

As discussed in the previous Section 4.1, the direction of the flux due to spatial lag follows the energy gradient, which is determined by the landward damping of flow velocities in the no-waves case. Therefore, the direction of that flux should not change if changing the local tidal asymmetries. In Fig. 12, the relative phase shift of the M4 to the M2 constituent at the boundary is changed, so that flow velocities are flood-dominant everywhere. This indeed affects the direction of the flux due to velocity asymmetry, but not the direction of the flux due to spatial lag (compare to Fig. 6, panel 2b). Extending the simulations to a spring-neap cycle (i.e. by adding the S2 and MS4 tidal constituents) does not result in overall differences with respect to the semidiurnal case. It is confirmed that the reference tidal forcing represents well the short-timescale dynamics of the basin.

Fig. 12

Residual fluxes of silt in the shallow subtidal region for a no-waves case with flood-dominant boundary tide. In comparison to Fig. 6, panel 2b, the pattern of the net flux due to velocity asymmetry changes, but the pattern due to spatial lag does not

4.3 Comparison with previous studies

Pritchard (2005) considered a channel whose width decreases landwards. His semi-analytical Lagrangian model showed that sediment fluxes are one order of magnitude smaller when advection is neglected, except for relatively coarse fractions. Waves were however neglected in that study. This result well agrees with the difference in magnitudes between spatial lag and velocity asymmetry in our no-waves simulation, even if the geometries of the schematized basins are different.

Our model results show that spatial lag is a dominant mechanism for relatively fine sediments. The net sediment flux follows the decreasing level of hydrodynamic energy in landward direction. This explains why sediment can be imported despite ebb-dominant tidal asymmetries, a result found also by Cheng and Wilson (2008) with a simplified analytical model.

Conversely, the model of Van Leeuwen et al. (2003) showed no relevance of lag-driven transport, as the sediment fluxes computed with the Engelund-Hansen formulation were not different from those computed from the advection-diffusion equation. The equation contained a constant deposition coefficient as a proxy for settling lag. A rectangular basin with a grain size of 200 μm and a constant bed level of − 2 m were considered. Our model is in agreement, showing that a grain size of 150 μm is already too coarse to experience lag effects in the shallow subtidal region.

In order to observe a consistent effect on the sediment dynamics, our model needs somewhat larger waves (H _s  > 45 cm) than those observed by Green (2011, H _s  < 10 cm), modeled by Waeles et al. (2004, H _s  = 5 cm) or measured in the Wadden Sea for the yearly average wind speed (H _s  < 20–30 cm, data available at www.openearth.nl). This can be ascribed to an underestimation of total bed-shear stresses due to the lack of the Grant and Madsen’s (1979) formulation and to the underestimation of tidal velocities. Especially during ebb (Fig. 7, x > 0.7), the absence of tidal creeks in the model slows down the flow in the intertidal region. Our schematized forcing also does not consider water-level setup (which can be a consistent percentage of the total water depth in shallow areas), nor intra-tidal variations of wind speed, whose coupling with the tidal phase can have an effect on net transport (Talke and Stacey 2008).

Elias (2006) compared the fluxes obtained with Groen’s (1967) formulation and the Delft3D morphology module (which considers an advection-diffusion equation with our same expression of the adaptation time). The former method could not reproduce the observed import of sand (250 μm) through the Texel inlet (Wadden Sea), whereas the latter method could. The author attributed the failure of Groen’s formulation to the neglected gradients in velocities and concentrations, corresponding to the spatial lag mechanism in our conceptual framework. Our model results partially agree. The tidally averaged flux obtained with Groen’s (1967) formulation is the sum of velocity asymmetry and temporal lag, which results in net seaward fluxes. However, the net landward flux by spatial lag is insufficient to cause the import of a sand fraction (150 μm, Fig. 6 panel 3a) which is finer than the fraction considered by Elias (2006). Since we prescribe the time-relaxed equilibrium concentration at the open boundary, our model prevents the possibility of a large concentration gradient between the inlet channel and the ebb-tidal delta, which can be relatively much more turbid due to long-shore transport and wave resuspension.

These comparisons show that our approach is in agreement with previous studies.

4.4 Residual transport and balancing mechanisms

A progressive landward fining of the bed composition is observed in the Wadden Sea (Flemming and Ziegler 1995), according to the decreasing level of hydrodynamic energy (Bartholoma and Flemming 2007). Hence, the morphological change in the deep channels near the inlet is determined by sand transport. Sand transport is governed by velocity asymmetry in our model, and tidal asymmetries are generally ebb-dominant in those channels (Friedrichs et al. 1992). Small-amplitude waves are ineffective. In the deep channels, the processes we consider cannot explain equilibrium, which requires import of sediment to keep pace with sea-level rise, or zero net transport if sea-level rise is not considered.

Besides ebb-tidal delta dynamics (mentioned in the previous section), other neglected processes could change magnitude and direction of the net sediment fluxes. Recent studies are directing to the importance of wind-driven circulation (e.g., Duran-Matute et al. 2016). In the Wadden Sea, wind-driven flow is capable of pushing large amounts of water and steer the sediment pathways so they overshoot the channel network and cross the watersheds between the sub-basins (Sassi et al. 2015). Baroclinic processes (Burchard et al. 2008; Jay and Musiak 1996), penetration of ocean swells (Talke and Stacey 2008), variability in composition and erodibility of the seabed (Friedrichs et al. 1998), lateral-exchange processes (Ralston and Stacey 2005) can all play a role. These processes can result in additional mechanisms and/or influence the mechanisms we considered. For instance, wind-driven flows or the superposition of wave propagation and tidal currents with different angles may change the asymmetries in peak flow velocities or flow acceleration/deceleration. In our schematized 1D model, these effects cannot be accounted for. Tidal asymmetries can also be influenced by seasonal and inter-annual variability of amplitudes and phases of the tidal constituents. However, we adopted the well-received assumption of net sediment transport being governed by the M2 and M4 constituents, whose temporal variability is small in the Wadden Sea (Gräwe et al. 2014). Chu et al. (2015) investigated the importance of including more constituents into the modeled tidal forcing, concluding that interactions among M0, M2, M4, and M6 are the most important in absence of river discharge.

The processes mentioned above and even rainfall (Tolhurst et al. 2006) may be important in the shallow subtidal and intertidal regions as well. However, silt and mud fractions here contribute to morphological changes. Therefore, our study supports the possibility of explaining tidal flats’ dynamic equilibrium as a simplified balance between tidal flow and wave resuspension. This is in agreement with previous studies (Sub-section 2.3.4). Sufficiently wide tidal flats typically feature flood-dominant transport regardless of the tidal asymmetries in the deeper zone (Friedrichs et al. 1992). If we prescribe an increasingly ebb-dominant tide at the open boundary of our model, we only shift the location of transition to flood-dominance landward. The wave-induced component of bed-shear stress can overturn the direction of residual transport by directly altering all three tidal mechanisms (velocity asymmetry, temporal lag, spatial lag). This indicates that wave resuspension can be a counterbalancing effect if the sediment import exceeds the amount needed to keep pace with sea-level rise (or if there is no sea-level rise).

Our model results show that the effectiveness of lag-driven transport rapidly decreases with decreasing water depths. However, spatial lag can still be the dominant mechanism for a muddy tidal flat (Fig. 6, panel 1c). Therefore, in order to achieve equilibrium, the flat’s profile has to adjust so that the energy gradient becomes null. This is in agreement with the renowned theory of Friedrichs and Aubrey (1996), although that considers the gradient in maximum bed-shear stress. We consider the time-averaged exceedance of the critical bed-shear stress (the erosion potential) instead. In this regard, a space-varying erosion threshold due to, e.g., biostabilization/bioturbation processes can also play a role in determining the energy gradient.

By contrast, a recent study of Maan et al. (2015) introduced the possibility of a perpetual imbalance of the tidal flat’s profile, due to a positive self-feedback of the processes. In other words, accretional (erosional) profiles tend to keep on accreting (eroding). If that is the case, the morphodynamic feedback caused by tidal flow and small-amplitude waves cannot explain a dynamic equilibrium, which has to be sought in other mechanisms like those mentioned regarding the deep subtidal region.

5 Summary and conclusions

The first part of the paper reviews the barotropic, tide-induced mechanisms of net sediment transport in tidal basins, viz. tidal asymmetries and lag effects. The dichotomy of adopting different frames of reference (Lagrangian for the lag effects and Eulerian for tidal asymmetries) to define the mechanisms makes a comparison complicated. Furthermore, it was highlighted that the effect of wave resuspension on sediment concentrations, albeit recognized as important in various studies, has not been systematically included in the treatment of the transport mechanisms.

The review concludes that the current classification is not suited for numerical, process-based models at the basin scale, as somewhat crude assumptions are needed and/or or the computational effort becomes unfeasible. Therefore, we reconceptualize the mechanisms in a unified Eulerian framework: velocity asymmetry, i.e., net transport of equilibrium concentrations; spatial lag and temporal lag, i.e., net transport due to spatial and local perturbations of the equilibrium concentration, respectively. A methodology is proposed to decompose these 3 tidally averaged fluxes of suspended sediment transport from the results of process-based models.

The second part of the paper applies the methodology to a schematized model of the Vlie basin, Wadden Sea. The methodology is proved to be consistent with the conceptual framework and model results agree with previous studies. The aggregation of multiple mechanisms into only 3 categories prevents the possibility of discriminating the individual processes, but the bulk effect of conceptually coherent mechanisms is retained. The spatial lag mechanism quantifies Friedrichs’s (2012) concept of net sediment transport driven by gradients of hydrodynamic energy.

Lag-driven transport can be the dominant component of the total net transport depending on the position in the basin and on the grain size. In relatively shallow channels, lag-driven transport can promote import of silt and mud despite ebb-dominant tidal asymmetries. Hence, models assuming the instantaneous adaptation of concentrations to varying flow conditions likely fail to reproduce the correct sediment fluxes. In absence of wave forcing, the same conclusion holds for models that consider an adaptation time but neglect advection in the sediment mass balance, as spatial lag effects are dominant, while local lag effects are negligible.

The magnitude of lag-driven transport rapidly decreases with decreasing water depths. Onto the tidal flats, spatial lag is effective only for very fine sediment and velocity asymmetry is the dominant mechanism of sediment import. In presence of waves, temporal lag becomes the main transport mechanism for silt and mud, but it results in net seaward fluxes. Waves can change the direction of the net fluxes caused by all 3 tidal mechanisms from landward to seaward. This supports the possibility of explaining tidal flats’ equilibrium as a simplified balance between barotropic tidal mechanisms and wave resuspension.

However, such an explanation cannot hold for subtidal channels. Here, small-amplitude waves are ineffective and morphological change is governed by sand transport, which is dominated by the ebb-dominant velocity asymmetry. Hence, balancing mechanisms have to be sought among the many processes neglected in this study, especially wind- and wave-driven circulation. Our conclusions encourage further tests of our conceptual framework and methodology with more complex and comprehensive numerical models.