Weakly complete domains in Grauert-type surfaces

Abstract

The aim of this short note is to investigate the geometry of weakly complete subdomains of Grauert-type surfaces, i.e., open connected sets D, sitting inside a Grauert-type surface X, which admit a smooth plurisubharmonic exhaustion function. We prove that they are either modifications of Stein spaces or Grauert-type surfaces themselves, and we apply these results to the special case of Hopf surfaces.

1 Introduction

A weakly complete space is a complex space which admits a plurisubharmonic exhaustion function; if the function is strictly plurisubharmonic outside a compact set, then the space is a modification of a Stein space.

Understanding the geometry of weakly complete spaces can be thought as a generalization of the classical Levi problem; in [4], Slodkowski, Tomassini and the author classified weakly complete surfaces which admit a real analytic plurisubharmonic exhaustion function. We refer to [3] for a review of some examples and the main steps of the proof; the result, loosely stated, says that such a complex surface is either holomorphically convex or the regular level sets of the exhaustion are Levi-flat hypersurfaces foliated in dense complex curves.

These last instances are called Grauert-type surfaces.

The aim of this short note is to investigate the geometry of weakly complete subdomains of Grauert-type surfaces, i.e., open connected sets D, sitting inside a Grauert-type surface X, which admit a smooth plurisubharmonic exhaustion function.

Instances of this question can be found, for example, in the works of Miebach (see [2]) and Levenberg and Yamaguchi (see [1]), where the problem is raised for Hopf surfaces.

It turns out that a weakly complete domain in a Grauert-type surface can either be a modification of a Stein space or a Grauert-type surface itself; in particular, this implies a kind of stability result, namely that, if the ambient space X admits a real analytic plurisubharmonic exhaustion function, then every weakly complete domain $\varOmega \subseteq X$ can be endowed with a real analytic plurisubharmonic exhaustion function.

The proof we present relies on some observations that hold true not only for Grauert-type surfaces, but also for holomorphically convex ones; therefore, we present our results for any weakly complete surface with a real analytic plurisubharmonic exhaustion function.

2 The kernel of a weakly complete space

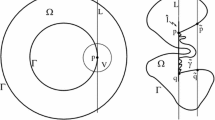
Let X be a weakly complete complex surface, endowed with a real analytic plurisubharmonic exhaustion function $\alpha :X\rightarrow {{\mathbb {R}}}$; suppose also that $D\subseteq X$ is a weakly complete domain, with an exhaustion function $\phi :D\rightarrow {{\mathbb {R}}}$ which is plurisubharmonic and smooth.

Following [6], we denote by $\Sigma ^1_X$ and $\Sigma ^1_D$ their kernels; namely, $\Sigma ^1_X$ is the set of points of X where every plurisubharmonic exhaustion function fails to be strictly plurisubharmonic.

By [6, Lemma 3.1], we can suppose that both $\alpha$ and $\phi$ are minimal for X and D, respectively, i.e., that $\Sigma ^1_X$ is exactly the set of points where $\alpha$ is not strictly plurisubharmonic and $\Sigma ^1_D$ is exactly the set of points where $\phi$ is not strictly plurisubharmonic. Moreover, by [4, Proposition 3.1], we can assume that both $\alpha$ and $\phi$ are nonnegative.

The following lemma collects some properties of kernels and minimal functions that we will need later on.

Lemma 2.1

Let X, D, $\alpha$, $\phi$ be as above. Then

• (1) $\Sigma ^1_D\subseteq \Sigma ^1_X$

• (2) for every $p\in \Sigma ^1_D$ which is a regular point for $\phi$, $d\alpha (p)=\lambda _pd\phi (p)$

• (3) for every $p\in \Sigma ^1_D$, $d\phi (p)$ vanishes on the kernel of $\partial \overline{\partial }\phi (p)$.

Proof

Take a point $p\in D$; if $p\not \in \Sigma ^1_X$, then the Levi form of $\alpha$ is positive definite at p, so $\alpha +\phi$ is a plurisubharmonic exhaustion function for D which is strictly plurisubharmonic at p; hence, $p\not \in \Sigma ^1_D$. This proves (1).

Now, observe that, if $\psi$ is a nonnegative plurisubharmonic function and q is a regular point for $\psi$, then

$$\begin{aligned} \partial \overline{\partial }\psi ^2=2(\partial \psi \wedge \overline{\partial }\psi + \psi \partial \overline{\partial }\psi ) \end{aligned}$$

is again positive semidefinite and the kernel of the associated linear map is given by the intersection of the kernel of $\partial \overline{\partial }\phi$ and the kernel of $\partial \psi$ (or, as $\psi$ is real valued, of $d\psi$). Therefore, if $p\in \Sigma ^1_D\subseteq \Sigma ^1_X$, then both $\phi$ and $\phi ^2$ must both have degenerate Levi forms at p; hence, $d\phi$ has to vanish on the kernel of $\partial \overline{\partial }\phi$. So (3) is proved.

Now, consider $\phi ^2+\alpha ^2$. In order for its Levi form to be degenerate at p, the kernels of $d\phi$ and $d\alpha$ and the kernels of $\partial \overline{\partial }\phi$ and $\partial \overline{\partial }\alpha$ must all coincide; hence, (2) follows. $\square$

From the Main Theorem in [4], in particular it follows that, for every $p\in \Sigma ^1_X$, regular point for $\alpha$, there exist an irreducible complex curve $F_p$ and an injective holomorphic map $i_p:F_p\rightarrow X$ such that $p\in C_p=i(F_p)\subseteq \Sigma ^1_X\cap \{\alpha =\alpha (p)\}$. Moreover, $T_pC_p$, if defined, is the kernel of $\partial \overline{\partial }\alpha (p)$.

Proposition 2.2

Consider $p\in \Sigma ^1_D$ and suppose that $\phi (p)$ is a regular value for $\phi$. Then $C_p\subseteq \Sigma ^1_D$.

Proof

By [6, Lemma 4.1], $\Sigma ^1_D\cap \{\phi =\phi (p)\}$ is foliated in complex curves; let $S_p$ be the leaf passing through p. By Lemma 2.1-(2), as $\phi$ is constant along $S_p$, so it is $\alpha$. Therefore, the immersed complex curve $S_p$ sits in $\Sigma ^1_D\cap \{\phi =\phi (p)\}$ as well as in $\Sigma ^1_X\cap \{\alpha =\alpha (p)\}$. But the latter, by the Main Theorem in [4], is either union of a finite number of irreducible compact curves or it is a real three-dimensional space foliated with complex leaves, which are then the only complex curves in it. Therefore, $S_p=C_p$.$\square$

Putting these observations together with the geometric structure of X given by the Main Theorem in [4], we obtain the result we claimed.

Theorem 2.3

Let X be a weakly complete complex surface endowed with a real analytic plurisubharmonic exhaustion function $\alpha :X\rightarrow {{\mathbb {R}}}$; consider $D\subseteq X$ a domain with a ${\mathcal {C}}^\infty$ plurisubharmonic exhaustion function $\phi :D\rightarrow {{\mathbb {R}}}$. Then, one of the following is true:

• (1) D is a modification of a Stein space

• (2) both D and X are union of complex curves

• (3) both D and X are Grauert-type surfaces.

Proof

We separate two cases.

First case

If we find a point $p\in \Sigma ^1_D$ and a minimal function $\psi$ for D such that the level set

$$\begin{aligned} Z_{\psi }(p)=\{q\in D\ :\ \psi (q)=\psi (p)\} \end{aligned}$$

is regular for $\psi$, then, by Proposition 2.2, $C_p\subseteq \Sigma ^1_D\subseteq D$.

Obviously, also the closure of $C_p$ will be contained in D; in the case of Grauert-type surfaces, this implies that D contains the connected component of the level set of $\alpha$ which contains p.

Now, if X is fibered in compact curves, we have a (holomorphic) proper map with connected fibers $F:X\rightarrow T$, where T is an open connected Riemann surface. If X is a surface of Grauert type with $M=\min \alpha$ of real dimension 2, then there is a (pluriharmonic) proper map [4, Main Theorem] with connected fibers [5, Theorem 3.1] $F:X{\setminus } M\rightarrow T$, where T is the real line. If M has real dimension 3, up to passing to a double cover $X^*$, we find a (pluriharmonic) proper map with connected fibers $F:X^*\rightarrow T$, where T is an open connected subset of the real line.

In all these three scenarios, we have a proper map with connected fibers $F:X^*\rightarrow T$, where $X^*$ is either X, $X{\setminus } M$ or a double cover of X and T is either an open connected Riemann surface or an open connected subset of the real line.

We define

$$\begin{aligned} \varOmega =\{x\in T\ :\ F^{-1}(x)\subseteq D\} \end{aligned}$$

and, by the first part of this proof, we know that $\varOmega \ne \emptyset$; we also set $V=F(D)$. We know that V is open and connected.

Consider a sequence $\{x_n\}\subset \varOmega$, converging to a point $x\in V$. If the fibers of F are irreducible compact complex curves, then obviously any plurisubharmonic function is constant on them. If the fibers of F are smooth Levi-flat hypersurfaces with dense complex leaves, then again any plurisubharmonic function is constant on them (see the end of the proof of [4, Corollary 3.8]); $\alpha$ being real analytic and proper, its critical values cannot accumulate, so, up to passing to a subsequence, we can suppose that $F^{-1}(x_n)$ is always contained in a smooth Levi-flat hypersurface. So, in both cases, as $F^{-1}(x_n)$ is contained in D, then $\phi$ is constant on it, for every n.

For every $p\in F^{-1}(x)\cap D$ (which is nonempty), there is a sequence of points $p_n$ such that $p_n\in F^{-1}(x_n)$, $p_n\rightarrow p$. This implies that $\phi$ is constant on $F^{-1}(x)\cap D$, but then $F^{-1}(x)\subset D$, because $\phi$ is an exhaustion function and the fibers of F are compact and connected. Hence, $\varOmega$ is closed in V.

On the other hand, if $x\in \varOmega$, then $\phi$ is constant on $F^{-1}(x)$, which is then a compact subset of D. By an easy topological argument, there exists a neighborhood U of $x\in T$ such that $F^{-1}(U)\subseteq D$, i.e., $U\subseteq \varOmega$, i.e., $\varOmega$ is open in V.

Therefore, $\varOmega$ is both open and closed in V, which is connected; so $\varOmega =V$, i.e., $D=F^{-1}(V)$.

Second case

Suppose that for every point $p\in \Sigma ^1_D$, the level set $Z_\phi (p)$ is singular. By Sard’s theorem, there exists a sequence $\{c_n\}_{n\in {\mathbb {N}}}\subseteq {{\mathbb {R}}}$ of regular values of $\phi$ such that $c_n\rightarrow +\infty$; hence, there exists a sequence of regular level sets $Z_\phi (p_n)$ with $p_n\rightarrow bD$.

By hypothesis, none of these level sets intersects $\Sigma ^1_D$, so, $\phi$ being minimal, all these levels are strongly pseudoconvex. By a standard argument, this implies that D is a modification of a Stein space. $\square$

Remark 2.1

All the contents of this section, apart from the second case in the previous theorem, hold when $\phi$ is supposed to be only ${\mathcal {C}}^2$; however, in order to apply Sard’s theorem, we need $\phi$ to be at least ${\mathcal {C}}^4$.

3 Applications

One special case of weakly complete surfaces with a real analytic plurisubharmonic exhaustion function is Hopf surfaces with one compact curve removed (see [4, Section 2] for a worked example). Applying Theorem 2.3 to this particular case, we obtain a different proof for the Main Theorem in [2] and Theorem 1.1. in [1], under the hypothesis of the existence of a smooth plurisubharmonic exhaustion.

More generally, suppose X is the total space of a topologically trivial line bundle over a compact Riemann surface M; if the class in $H^1(M, {\mathcal {S}}^1)$ associated with the bundle is unipotent, then X is fibered in compact curves; otherwise, it is a Grauert-type surface (see [4, Section 2] and [5, Section 4] for related discussions and examples).

In both cases, we have a minimal plurisubharmonic function whose only critical level is the minimum level, coinciding with M; so, any open set containing M will also contain a regular level set of the exhaustion function.

Combining these observations with Theorem 2.3, we obtain the following

Corollary 3.1

Suppose X is the total space of a topologically trivial line bundle $\xi$ over a compact Riemann surface M and let $D\subset X$ be a weakly complete domain with a smooth plurisubharmonic exhaustion. Then one of the following happens:

• (1) D is Stein

• (2) both D and X are fibered in complex curves

• (3) both D and X are Grauert-type surfaces.

Proof

From Theorem 2.3 we know that, if cases (2) and (3) don’t apply, then D is a modification of a Stein space. However, if D were not Stein, then it would contain some compact curves. If X is a surface of Grauert type, the only compact curve in it is M, which doesn’t have any Stein neighborhood; on the other hand, if X is fibered in complex curves, as soon as D contains one of them, it is a union of curves, repeating the argument in the end of the first case in the proof of Theorem 2.3.

Therefore, D is Stein. $\square$

Remark 3.1

The proof we have just given applies whenever X is a weakly complete surface which admits a real analytic plurisubharmonic exhaustion function whose only critical level set is the minimum level set.