Skip to main content
SpringerLink
Log in

Symmetric Exponential Integrators with an Application to the Cubic Schrödinger Equation

  • Published:
Foundations of Computational Mathematics Aims and scope Submit manuscript

Abstract

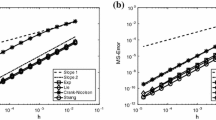
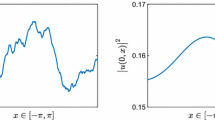
In this article, we derive and study symmetric exponential integrators. Numerical experiments are performed for the cubic Schrödinger equation and comparisons with classical exponential integrators and other geometric methods are also given. Some of the proposed methods preserve the L 2-norm and/or the energy of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. J. Ablowitz and J. F. Ladik, A nonlinear difference scheme and inverse scattering, Stud. in Appl. Math. 55(3) (1976), 213–229.

    MathSciNet  Google Scholar 

  2. H. Berland, A. L. Islas, and C. M. Schober, Conservation of phase space properties using exponential integrators on the cubic Schrödinger equation, Technical report 1/06, Norwegian Institute of Science and Technology (2006), submitted to J. Comput. Phys.

  3. H. Berland, B. Skaflestad, and W. M. Wright, EXPINT—A MATLAB package for exponential integrators, ACM Trans. Math. Softw. 33(1) (2007).

  4. C. Besse, A relaxation scheme for the nonlinear Schrödinger equation, SIAM J. Numer. Anal. 42(3) (2004), 934–952 (electronic).

    Article  MathSciNet  MATH  Google Scholar 

  5. T. J. Bridges and S. Reich, Multi-symplectic integrators: numerical schemes for Hamiltonian PDEs that conserve symplecticity, Phys. Lett. A 284(4/5) (2001), 184–193.

    Article  MathSciNet  MATH  Google Scholar 

  6. B. Cano, Conserved quantities of some Hamiltonian wave equations after full discretization, Numer. Math. 103(2) (2006), 197–223.

    Article  MathSciNet  MATH  Google Scholar 

  7. J. Certaine, The solution of ordinary differential equations with large time constants, in Mathematical Methods for Digital Computers, pp. 128–132, Wiley, New York, 1960.

    Google Scholar 

  8. A. Durán and J. M. Sanz-Serna, The numerical integration of relative equilibrium solutions. The nonlinear Schrödinger equation, IMA J. Numer. Anal. 20(2) (2000), 235–261.

    Article  MathSciNet  MATH  Google Scholar 

  9. Z. Fei, V. M. Pérez-García, and L. Vázquez, Numerical simulation of nonlinear Schrödinger systems: a new conservative scheme, Appl. Math. Comput. 71(2/3) (1995), 165–177.

    Article  MathSciNet  MATH  Google Scholar 

  10. E. Hairer, Symmetric projection methods for differential equations on manifolds, BIT 40(4) (2000), 726–734.

    Article  MathSciNet  MATH  Google Scholar 

  11. E. Hairer, C. Lubich, and G. Wanner, Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd edn., Springer Series in Computational Mathematics, Vol. 31, Springer, Berlin, 2006.

    MATH  Google Scholar 

  12. A. L. Islas, D. A. Karpeev, and C. M. Schober, Geometric integrators for the nonlinear Schrödinger equation, J. Comput. Phys. 173(1) (2001), 116–148.

    Article  MathSciNet  MATH  Google Scholar 

  13. A. L. Islas and C. M. Schober, On the preservation of phase space structure under multisymplectic discretization, J. Comput. Phys. 197(2) (2004), 585–609.

    Article  MathSciNet  MATH  Google Scholar 

  14. J. D. Lawson, Generalized Runge–Kutta processes for stable systems with large Lipschitz constants, SIAM J. Numer. Anal. 4 (1967), 372–380.

    Article  MathSciNet  MATH  Google Scholar 

  15. J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, 2nd edn., Texts in Applied Mathematics, Vol. 17, Springer, New York, 1999.

    MATH  Google Scholar 

  16. R. I. McLachlan, Symplectic integration of Hamiltonian wave equations, Numer. Math. 66(4) (1994), 465–492.

    MathSciNet  MATH  Google Scholar 

  17. B. Minchev and W. M. Wright, A review of exponential integrators for semilinear problems, Technical report 2/05, Department of Mathematical Sciences, NTNU, Norway (2005), http://www.math.ntnu.no/preprint/.

  18. S. Reich, Multi-symplectic Runge–Kutta collocation methods for Hamiltonian wave equations, J. Comput. Phys. 157(2) (2000), 473–499.

    Article  MathSciNet  MATH  Google Scholar 

  19. T. R. Taha and J. Ablowitz, Analytical and numerical aspects of certain nonlinear evolution equations. II. Numerical, nonlinear Schrödinger equation, J. Comput. Phys. 55(2) (1984), 203–230.

    Article  MathSciNet  MATH  Google Scholar 

  20. A. Zanna, K. Engø, and H. Munthe-Kaas, Adjoint and selfadjoint Lie-group methods, BIT 41(2) (2001), 395–421.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, NTNU, 7491, Trondheim, Norway

    Elena Celledoni, David Cohen & Brynjulf Owren

Authors
  1. Elena Celledoni
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Cohen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Brynjulf Owren
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Brynjulf Owren.

Additional information

Dedicated to Professor Arieh Iserles on the Occasion of his Sixtieth Birthday.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Celledoni, E., Cohen, D. & Owren, B. Symmetric Exponential Integrators with an Application to the Cubic Schrödinger Equation. Found Comput Math 8, 303–317 (2008). https://doi.org/10.1007/s10208-007-9016-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10208-007-9016-7

Keywords

Mathematics Subject Classification (2000)

Search

Navigation