The role of passing network indicators in modeling football outcomes: an application using Bayesian hierarchical models

Abstract

Passes are undoubtedly the more frequent events in football and other team sports. Passing networks and their structural features can be useful to evaluate the style of play in terms of passing behavior, analyzing and quantifying interactions among players. The present paper aims to show how information retrieved from passing networks can have a relevant impact on predicting the match outcome. In particular, we focus on modeling both the scored goals by two competing teams and the goal difference between them. With this purpose, we fit these outcomes using Bayesian hierarchical models, including both in-match and network-based covariates to cover many aspects of the offensive actions on the pitch. Furthermore, we review and compare different approaches to include covariates in modeling football outcomes. The presented methodology is applied to a real dataset containing information on 125 matches of the 2016–2017 UEFA Champions League, involving 32 among the best European teams. From our results, shots on target, corners, and such passing network indicators are the main determinants of the considered football outcomes.

1 Introduction

New technologies, such as wearable devices, multiple-camera player trackers, and drone-based analysis of training sessions, are increasing the ways to retrieve data and provide new opportunities in team sports analysis. The statistical analysis of collected data recently spread in real applications concerning team sports and football especially (Albert et al. 2005; Memmert 2019).

In this applied field, most statistical methods focus on modeling football outcomes, such as the team winning, exact match result, scored goals, and ball possession. In fact, statistical models are useful to assess the main determinants that explain and/or predict football outcomes. In this sense, in-match indicators, political-economic factors, or socio-geographic features are often used as explanatory variables.

According to Egidi and Torelli (2020), two main types of statistical models can be distinguished in this context: result-based and goal-based. The first type is based on a multinomial outcome, typically constituted by the following categories: home win, draw, and home loss (labeled as 1, X, 2). The second one considers the number of goals scored by each competing team. For clarity, we propose to distinguish a further family of models characterized by the goal difference as the response variable. We decide to denote them as difference-based models, even if, sometimes, they are included among the goal-based models. In this paper, the difference-based and the goal-based approaches are considered.

Goal-based models are usually defined assuming a probability distribution suitable for counts to model the response. From the seminal work by Maher (1982), the use of conditionally independent Poisson distributions represents the default choice in modeling the number of scored goals by each team in a match. Some notable extensions are the works by Dixon and Coles (1997) and Rue and Salvesen (2000) that take into account changes in team conditions usually occurring along the season. Karlis and Ntzoufras (2003) proposed to include the possibility that scored goals are positively correlated within matches, specifying a bivariate Poisson distribution. On the other hand, the work by Karlis and Ntzoufras (2009) can be denoted as the first example of a difference-based model: the authors assumed a Skellam distribution to fit the goals-difference between two teams. Many of these fundamental contributions belong to the Bayesian framework, the inferential approach considered in this paper. Among the others, it is worth citing Baio and Blangiardo (2010), Egidi and Torelli (2020), and Manderson et al. (2018) as empirical applications based on Bayesian inference.

Besides individual skills of players, tactics and team strategies are key elements for succeeding in football, and appropriate methodology to deal with these elements is still under debate. Furthermore, network metrics are recently becoming more popular in football, as highlighted in Pena and Touchette (2012) and Clemente et al. (2015). In particular, network analysis is applied to football passing distributions: a relevant contribution is Grund (2012), and other interesting applications can be found in Gonçalves et al. (2017), Mclean et al. (2018), Clemente et al. (2020), and Ichinose et al. (2021).This approach is also exploited in other team sports (see, e.g., Braham and Small 2018, for an application to Australian football). Passing networks present some advantages: they help to detect patterns or strong/weak ties among players and their positions in the line-up. They also provide valuable evidence of players’ skills, tactics, and connections between positions. Unfortunately, the data at the individual level, required to generate passing networks, are open access only for the major international competitions.

The first main contribution of the paper is to show the potential of Bayesian hierarchical models in either managing covariates and finding the determinants of football outcome. In fact, the flexibility of Bayesian models and the usage of appealing computational tools allow us to review and discuss the practical meaning of different model specifications, considering diverse dependence relationships between the response and the covariates. Several probabilistic programming languages can be employed in a Bayesian framework to draw samples from the posterior distributions of the parameters. The models presented in this work are estimated using Stan (Stan Development Team 2020), and the code is available as supplementary material. We aim to carefully compare several expressions for the linear predictors, assessing their potential drawbacks on real data, in order to advise applied researchers and experts. Regularized horseshoe priors (Piironen and Vehtari 2017) are assumed for the regression coefficients to control their posterior variance, avoid multicollinearity, and limit the occurrence of over-fitting issues that might lead to poor out-of-sample performances. Regularized estimates of the coefficients were considered in recent works (Groll et al. 2015; Schauberger et al. 2018) from a pure frequentist perspective.

A further aim of this work is to exploit performance indicators derived from passing networks in the analysis football outcomes, including network indices as explanatory variables. We decide to take advantage of this information with other in-match variables to explore their interplay in determining the game outcome. In fact, passes represent more than $80\%$ of the events in football (Cintia et al. 2015), and they convey crucial information on the strength of a team. To summarize, we include network indices with team-level control variables (usually free available match statistics) to suggest to football insiders which factors are the most important in determining the outcome on the pitch.

To the best of our knowledge, none of the previously cited works takes into account the strength of relationships among players, neither the type of interactions among them. Exceptions can be found in Grund (2012), which does not use in-match covariates, and, more recently, in Diquigiovanni and Scarpa (2019), which exploited network-based clusters to model the scored goals. Furthermore, Ievoli et al. (2021) used network indicators to model the probability of winning the game for a team. From a slightly different perspective, Carpita et al. (2019) included the a priori evaluation of players’ abilities (involving passing skills) in predicting the win, without using passing network information.

The rest of the paper is organized as follows: in Sect. 2, we present the main variables of our analysis, dividing them into in-match variables and network summary measures. In Sect. 3, we introduce goal based and difference based Bayesian hierarchical models, using four different specifications of the linear predictor. Section 4 contains the main results of proposed models applied to a real dataset regarding the 2016-2017 UEFA Champions League (UCL). They are followed by a brief discussion regarding the meaning of our results and their practical implications in football (Sect. 5). Finally, concluding remarks are summarized in Sect. 6.

2 Variable measurement

In this section, we define the set of variables that will be used in the proposed statistical models. The football outcomes and the in-match covariates are firstly introduced, then we skip to the definition of the network-based summary measures. It is worth stressing that, for each generic match g, we record observations both for the home team (H) and the away team (A).

2.1 Football outcomes

Throughout the paper, the football outcome is defined in the following ways:

• (a) $y_\mathrm{g}^\mathrm{H}$ is the number of goals scored by the home team

• (b) $y_\mathrm{g}^\mathrm{A}$ is the number of goals scored by the away team

• (c) $z_\mathrm{g} = y_\mathrm{g}^\mathrm{H}-y_\mathrm{g}^\mathrm{A}$ is the difference between goals scored by two competing teams (or margin of victory).

Definitions (a) and (b) characterize the goal-based modeling approach and can be found, for instance, in Maher (1982), Dixon and Coles (1997), Rue and Salvesen (2000), and Karlis and Ntzoufras (2003). On the other hand, definition (c) refers to the difference-based approach and appears in Karlis and Ntzoufras (2009) or Manderson et al. (2018), among others.

2.2 In-match variables

Regarding the in-match covariates, we collect indices for the two competing teams of each match. The focus is mainly on conventional quantities often used in applied works (Castellano et al. 2012; Carpita et al. 2015; Schauberger et al. 2018; Lepschy et al. 2020). These variables refer to actual events in match g, and their observed values are stored in vectors ${{\varvec{x}}}^\mathrm{H}_\mathrm{g}$ and ${{\varvec{x}}}^\mathrm{A}_\mathrm{g}$ for the home team and the away team, together with the network-based variables. The set of in-match variables is described in the following.

• Shots on target: it is the number of attempted shots on goal per team in a match. It measures the ability to produce concrete opportunities.

• Corners: it is the count of obtained corner kicks, which can be another relevant output of the offensive actions.

• Fouls suffered: it is the raw number of suffered fouls (including hands), which can interrupt the offensive actions.

• Ball possession: it is the ratio between the time in which a team plays the ball and the total match time.

• Distance: it is the sum of meters covered by all the players of a team, representing a synthetic measure of athletic skills.

2.3 Network-based variables

Network analysis deals with relational data, emphasizing the investigation of the structure generated between units, driven by quantity and quality of ties occurring among them. Network theory includes all possible methods to analyze data presenting interactions between a set of units (agents) to investigate patterns and community structures (Wasserman and Faust 1994).

A network is defined as the ordered triple $({\mathcal {V}}, {\mathcal {A}},{\mathcal {W}})$ consisting of a set of vertices $v \in {\mathcal {V}}$, a set of arcs $a \in {\mathcal {A}} \subseteq {\mathcal {V}} \times {\mathcal {V}}$, and a set of weights $\omega \in {\mathcal {W}}$. Both sets of vertices ${\mathcal {V}}$ and arcs ${\mathcal {A}}$ are assumed to be finite. An ordered pair of vertices denotes an arc through a function $\psi$: $\psi (v_i,v_j)~=~a_{ij} \in {\mathcal {A}}$, mapping the one-directional tie from vertex $v_i$ to $v_j$, with $i,j=1, \ldots , n$. The mapping $\omega :{\mathcal {A}} \rightarrow {\mathbb {R}}$ defines a weight related to each arc. A network can be expressed in the form of an adjacency matrix $P= \left( p_{ij}\right)$, with $p_{ij} = \omega (a_{ij})$ if $\exists \; a_{ij} \in {\mathcal {A}}$ and $p_{ij}=0$ otherwise and $i\ne j$. We also assume that “loops”, i.e., arcs connecting a vertex to itself, as are not allowed. Therefore, $p_{ij} = 0$ when $i=j$.

Table 1 Example of an adjacency matrix in football

Fig. 1

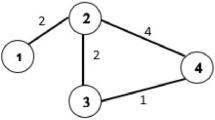
Graph of the team passing network of Arsenal (vs PSG, 09/13/2016), generated from the adjacency matrix illustrated in Table 1. Dark lines emphasize links presenting weights higher than the median of adjacency matrix

Table 2 Input variables setting scheme

In football, a specific adjacency matrix can be obtained for each match of a team. Considering the starting line-up, eleven players ($n=11$) are depicted in rows and columns of the matrix, and cells contains the number of completed passes between players of a given team. In practice, this matrix can be read in two different ways, i.e., row-wise and column-wise. In the former, a generic cell $p_{ij}$ contains the number of passes that i-th player gives to j-th player, while, in the latter, the cell expresses the number of passes that j-th player receives from i-th player. To summarize, this matrix is composed by 110 cells, since we assume that a player cannot pass the ball to himself, and it is generally not symmetric.

In Table 1, an example of adjacency matrix is reported. It concerns the team passing network distribution of Arsenal observed for the match against PSG of 09/13/2016. Figure 1 represents the directed and weighted graph obtained through the adjacency matrix of Table 1. Players $p_{i}$ are connected by arrows (representing the arcs), and the strength of the relationships (i.e., the number of passes) is expressed through the arrows’ width. The graph is obtained using the package igraph (Csardi and Nepusz 2006) in R software (R Core Team 2020). This representation primarily allows to make comparisons at the individual (micro) level involving players, but some information can also be extracted at the team (macro) level to evaluate the overall performance.

After introducing the passing networks, it is necessary to find techniques able to synthesize the information contained in them. Several network indices can be found in the literature (see, Wasserman 1994; Carrington et al. 2005; De Nooy et al. 2018, among others). They can be computed from team passing networks and interpreted as performance indicators (see, e.g., Clemente et al. 2016). We focus on some network summary measures that are able to capture the complexity of network topology with a meaningful interpretation for football. These indices are described in the following.

• Pass accuracy: at the team level, it is defined as the sum of ratios between completed ($P_i^\mathrm{c}$) and attempted ($P_i^\mathrm{a}$) passes for each i-th player. It is proposed as a measure of the overall technical skills of a football team since it may have a key role in creating offensive actions and, in some cases, can avoid to receive counterattacks from the opponent. To summarize, this index represents a “bridge” between in-match covariates and network summary measures.

• Network intensity: it is defined as $\text {Time}_\mathrm{e}^{-1}\sum _{i}\sum _{j} p_{ij}$, where $\text {Time}_\mathrm{e}$ is the actual ball possession time (in minutes), and $p_{ij}$ is the generic element of the adjacency matrix of a team in a match (e.g., see Table 1). Since it is crucial to take into account the real minutes of ball possession (i.e., excluding when the ball is out of play), we propose the usage of effective time of ball possession ($\text {Time}_\mathrm{e}$). This is a modification of the index introduced by Grund (2012), which used the overall time of ball possession instead of $\text {Time}_\mathrm{e}$. From a football perspective, this index quantify the passing speed of a team in a match, i.e., the aptitude to circulate the ball quickly among teammates.

• Network diameter: it is the geodesic distance between most distant vertices of a graph, without taking into account the link weights. Given a set of vertices of a network ${\mathcal {V}}$ and the geodesic distance d(u, v), measured between two vertices $u,v \in {\mathcal {V}}$, the diameter can be expressed as $\max _{u,v \in {\mathcal {V}}} d(u,v)$. High network diameter values express the ability to generate as many direct connections as possible in terms of passes, even considering that the theoretical maximum in our setting corresponds to the number of players (11). It can be also viewed as a measure of tactical variety (e.g., the ability to make cross-field passes).

• Reciprocity: it is computed as the proportion of mutual connections in a directed graph, i.e., the frequency of opposite counterpart of a directed arc also included in the graph. Given $L^{\leftrightarrow } = \{a \,| \, a \text{ is } \text{ a } \text{ bidirectional } \text{ arc }\} \subseteq {\mathcal {A}}$, reciprocity corresponds to $|L^{\leftrightarrow }|/|{\mathcal {A}}|$. In football, it measures the ability of two players to have mutual connections with each other. Moreover, it also evaluates the balance of a team in terms of passing directions. For example, high values of reciprocity can be related to the propensity of certain type of relationships, such as the so-called “give and go” or “wall passes”.

• Median of average nearest neighbors (MANN): it is computed as the median of the average nearest neighbors. For each player $p_i$, the average degrees of partners for the i-th vertex can be computed as (Clemente et al. 2016):

  $$\begin{aligned} \text{ ANN}_{i} = \dfrac{\sum _j \left( p_{ij} + p_{ji}\right) \left( p_{j\cdot } + p_{\cdot j}\right) }{2\left( p_{i \cdot } + p_{ \cdot i}\right) }, \end{aligned}$$

  where $p_{i \cdot }$ and $p_{\cdot i}$ are, respectively, the row and column marginal sums of the adjacency matrix. This is an individual index expressing the correlation levels between pairs of players. The overall index (MANN), at the team level, measures the cohesion in terms of passing behaviors: the presence of one or few key players on the pitch, in terms of completed and received passes, leads to higher values of this index.

• Third quartile of hub ($Q_3$-Hub): it is computed as the 75-th percentile of the individual hub indices. The algorithm to compute hubs can be found in Kleinberg et al. (2011). High values of such index are associated to players with good ability in passing the ball to other players. Hub players can be seen as play-makers of a team. Q$_3$-Hub can be considered a synthetic measure expressing the level of “play-making” of a team.

Table 2 has the role of summarizing the variables of this section, depicting their description, the covered dimension of the game, the domain, the mathematical expression (when required), and, lastly, the associated references. A detailed explanation on how passing network matrices can be processed to obtain graphs and compute the previously illustrated summary measures is provided as supplementary material, including code and data example.

3 Bayesian modeling of football outcomes

In this section, statistical models that will be estimated on UCL data are illustrated. Recalling the football outcomes defined in Sect. 2, we can distinguish two families of statistical models. Goal-based models are specified if the couple of scored goals $\left( y_g^\mathrm{H},y_g^\mathrm{A}\right)$ is considered as the response for match $g=1,\dots G$. Alternatively, difference-based models are fitted if the goal difference between the competing teams $z_g$ is employed as the response. Starting from goal-based models, the first setting we discuss relies on Maher (1982) model. He proposed to specify two conditionally independent Poisson distributions for the scored goals (labeled with IP in following):

$$\begin{aligned} y_g^\mathrm{H}|\lambda _g^\mathrm{H}\sim \hbox {Poi}\left( \lambda _g^\mathrm{H}\right) ,\quad y_g^\mathrm{A}|\lambda _g^\mathrm{A}\sim \hbox {Poi}\left( \lambda _g^\mathrm{A}\right) ;\quad g=1,\dots ,G. \end{aligned}$$

(1)

The Poisson parameters $\lambda _g^H$ and $\lambda _g^A$ are modeled specifying the following linear models on their logarithmic transformations:

$$\begin{aligned} \begin{aligned} \log \left( \lambda _g^\mathrm{H}\right)&=\mu +h+{{\varvec{u}}}_g^\mathrm{T}\varvec{\beta }_\mathrm{H}+\alpha _{\mathrm{H}_g}+\delta _{\mathrm{A}_g};\\ \log \left( \lambda _g^\mathrm{A}\right)&=\mu +{{\varvec{v}}}_g^\mathrm{T}\varvec{\beta }_\mathrm{A}+\alpha _{\mathrm{A}_g}+\delta _{\mathrm{H}_g}. \end{aligned} \end{aligned}$$

(2)

In football, such linear predictors are characterized by the following fixed components: a common location parameter $\mu$, a home effect parameter h, accounting for the possible favorable conditions that the team hosting the game may have, and a linear combination of p covariate values (${{\varvec{u}}}_g\in {\mathbb {R}}^p$ for the home team and ${{\varvec{v}}}_g\in {\mathbb {R}}^p$ for the away team) with the associated regression coefficients $\varvec{\beta }_\mathrm{H}$ and $\varvec{\beta }_\mathrm{A}$. Teams-crossed random effects are included too: $\alpha _t$ conveys the attacking ability of team $t=1,\dots ,T$, whereas $\delta _t$ concerns its defense ability. The subscripts of the effects ($H_g$ and $A_g$) represent the indices of teams involved in match g, remembering that the attacking effect of a given team and the defense effect of the opponent team concur in explaining the number of scored goals.

Karlis and Ntzoufras (2003) noted that setting a model by means of conditionally independent Poisson distributions might neglect the positive correlation that is commonly observed between the number of goals scored by the competing teams. To overcome this issue, they proposed to model the couples of scored goals through a bivariate Poisson (BP) distribution:

$$\begin{aligned} \left( y_g^\mathrm{H}, y_g^\mathrm{A}\right) |\lambda _g^\mathrm{H},\lambda _g^\mathrm{A},\lambda _g^\mathrm{C}\sim Biv\text {-}Poi\left( \lambda _g^\mathrm{H},\lambda _g^\mathrm{A},\lambda _g^\mathrm{C}\right) ;\quad g=1,\dots ,G. \end{aligned}$$

(3)

Under this model, the following moment’s expressions hold: ${\mathbb {E}}\left[ y_g^\mathrm{H}\right] =\lambda _g^\mathrm{H}+\lambda _g^\mathrm{C}$, ${\mathbb {E}}\left[ y_g^\mathrm{A}\right] =\lambda _g^\mathrm{A}+\lambda _g^\mathrm{C}$, and the covariance is ${\mathbb {C}}\left[ y_g^\mathrm{H},y_g^\mathrm{A}\right] =\lambda _g^\mathrm{C}$. For parameters $\lambda _g^\mathrm{H}$ and $\lambda _g^\mathrm{A}$, the same predictors of (2) are assumed, whereas for the correlation parameter, in line with Karlis and Ntzoufras (2003):

$$\begin{aligned} \log \left( \lambda _g^\mathrm{C}\right) =\mu _\mathrm{C}+\rho _{\mathrm{H}_g}+\rho _{\mathrm{A}_g}, \end{aligned}$$

(4)

where $\mu _\mathrm{C}$ is the baseline correlation level and $\rho _t$ is a team-specific random effect.

In parallel, moving to the framework of difference-based modeling, following Karlis and Ntzoufras (2009), we model the margin of victory $z_g$ assuming a Skellam distribution (Sk):

$$\begin{aligned} z_g|\lambda _g^\mathrm{H},\lambda _g^\mathrm{A}\sim Sk\left( \lambda _g^\mathrm{H},\lambda _g^\mathrm{A}\right) ;\quad g=1,\dots ,G. \end{aligned}$$

(5)

The Skellam distribution is defined as the difference between two Poisson distributions having intensity parameters $\lambda _g^\mathrm{H}$ and $\lambda _g^\mathrm{A}$, which are defined as in (2). We stress that, unlike goal-based models, the use of the $z_g$ leads to the loss of the match outcome magnitude, and the two Poisson intensity parameters do not directly pertain to the number of scored goals by a given team. On the other hand, assuming a Skellam distribution for the difference implies marginal distributions for the scored goals that are more flexible than the Poisson (even in the bivariate case). As a matter of fact, the BP model accounts for the correlation of the couple $(y_g^\mathrm{A},y_g^\mathrm{H})$ through a Poisson distribution (that has intensity $\lambda _g^\mathrm{C}$ in our notation), whereas, under the Sk model, the correlation is implicitly modeled by means of any discrete random variable. For further details of this aspect see Karlis and Ntzoufras (2009).

3.1 Prior distributions

Since we are in the Bayesian inferential framework, we need to specify a prior distribution for each parameter included in the model. Starting from the random effect vectors $\varvec{\alpha }$, $\varvec{\delta }$ and $\varvec{\rho }$, we assume them as a priori independent, following zero-mean Gaussian distributions:

$$\begin{aligned} \varvec{\alpha }|\sigma ^2_\alpha \sim {\mathcal {N}}_T\left( {\varvec{0}},\sigma ^2_\alpha {{\varvec{I}}}_{T}\right) ;\ \varvec{\delta }|\sigma ^2_\delta \sim {\mathcal {N}}_T\left( {\varvec{0}},\sigma ^2_\delta {{\varvec{I}}}_{T}\right) ;\ \varvec{\rho }|\sigma ^2_\rho \sim {\mathcal {N}}_T\left( {\varvec{0}},\sigma ^2_\rho {{\varvec{I}}}_{T}\right) , \end{aligned}$$

and the classical sum-to-zero constraints are imposed: $\sum _{t=1}^{T}\alpha _t=0$, $\sum _{t=1}^{T}\delta _t=0$, and $\sum _{t=1}^{T}\rho _t=0$. In doing so, the random effects capture the deviations due to the attacking and defensive abilities of the specific team from the fixed part of the linear predictor, i.e., the overall mean, the possible home effect, and the linear combination of coefficients with the observed covariates (Karlis and Ntzoufras 2003). To sample from the constrained posterior distribution, see the manual of the Stan software (Stan Development Team 2020).

The regression coefficients ($\varvec{\beta }_\mathrm{H}$ and $\varvec{\beta }_\mathrm{A}$) included in (2) might be estimated through the introduction of a penalty term. In fact, several variables could affect the response, all being included in the linear predictor. For this reason, regularization methods are used for variable selection since they shrunk to zero coefficient estimates related to negligible covariates, reducing the parameters’ variance. Among the others, Groll et al. (2015) and Tutz and Schauberger (2015) considered the LASSO framework, whereas the problem has not been tackled yet from the Bayesian perspective. A plethora of shrinkage priors for the regression coefficients are available (Bhadra et al. 2019), here we decide to adopt the regularized horseshoe prior by Piironen and Vehtari (2017): it easily allows to incorporate prior information about sparseness and can be interpreted as the continuous version of the popular spike-and-slab priors. The prior setting for the generic regression coefficient is defined as follows:

$$\begin{aligned}&\beta _{k,j}|\tau _k^2,\lambda _{k,j}^2\sim {\mathcal {N}}\left( 0,\tau _k^2{\tilde{\lambda }}_{k,j}^2\right) ,\ k\in \left\{ \mathrm{H},\mathrm{A}\right\} ,\ j=1,\dots ,p;\\&{\tilde{\lambda }}_{k,j}^2=\frac{c_k^2\lambda _{k,j}^2}{c_k^2+\tau _k^2\lambda _{k,j}^2}, \end{aligned}$$

where $\tau _k$ represents a global scale, $\lambda _{k,j}$ a local scale, and c is a further scale parameter that controls the prior assumed on the coefficients not shrunk toward 0, i.e., the slab part of the prior.

The hierarchy is completed assuming:

$$\begin{aligned}&\lambda _{k,j}\sim {\mathcal {C}}^+(0,1),\\&\tau _k\sim {\mathcal {C}}^+(0,\tau _0),\\&c^2_k\sim \hbox {Inv-Gamma}\left( \frac{\nu _\mathrm{slab}}{2},\frac{\nu _\mathrm{slab}}{2}s_\mathrm{slab}^2\right) , \end{aligned}$$

where $\nu _\mathrm{slab}$ and $s_\mathrm{slab}^2$ can be interpreted as the degrees of freedom and scale of the Student’s t prior on the slab part, since the prior on the regression coefficient tends to a ${\mathcal {N}}\left( 0,c^2_k\right)$ in absence of shrinking . The prior scale of $\tau _k$ is fixed as $\tau _0^2=p_0{\tilde{\sigma }}/\left( (p-p_0)\sqrt{G}\right)$: $p_0$ is interpreted as the prior number of expected non-null effects and ${\tilde{\sigma }}^2$ is the pseudo-variance of generalized linear models that in the Poisson case with logarithmic link can be fixed as the reciprocal of the sample mean (Piironen and Vehtari 2017).

Eventually, in line with Gelman et al. (2006), half-Student’s t priors are set for the scale hyperparameters $\sigma _\alpha$, $\sigma _\delta$ and $\sigma _\rho$, choosing 3 degrees of freedom. A non-informative Gaussian prior centered in zero having large variance is chosen for the parameters $\mu$, h, and $\mu _\mathrm{C}$.

3.2 Model specifications: linear predictors

One of this paper aims is to explore and compare possible relationships that can be assumed between the response variable and the covariates included in the model. As discussed in Sect. 2, variables listed in Table 2 are used as auxiliary information, and, referring to game g, they are contained in vector ${{\varvec{x}}}^\mathrm{H}_{g}$ for the home team and ${{\varvec{x}}}^\mathrm{A}_{g}$ for the away team.

Firstly, baseline models without any auxiliary information are considered. Throughout the paper, we will label this formulation of the linear predictors as $M_0$, where M will be replaced by the specified model (i.e., IP, BP, or Sk). Then, following Groll et al. (2015) and Groll et al. (2018), the differences between the covariates observed for the two teams in match g are used: we refer to this specification with $M_1$. With $M_2$, we indicate the most flexible model specification considered: we link each linear predictor to the covariates observed on the specific team. Finally, the latter framework is simplified in $M_3$ by assuming a common vector of regression coefficients for both the competing teams. Table 3 has the role of summarizing the considered specifications in terms of algebraic relationships and restrictions imposed on equations terms in (2).

Table 3 Assumptions of linear predictors under the different models

3.3 Model checking and model selection

To draw samples from the posterior distribution of the parameters that characterize the models described in this section, the Stan software is used through its R interface rstan. In this way, Markov Chain Monte Carlo (MCMC) samples are obtained from each parameters posterior distribution and can be used to carry out inference. Any posterior distribution can be synthesized by computing Monte Carlo estimates of the usual summary statistics such as the mean, the standard deviation, and the quantiles, that are used to produce the credible intervals.

The natural way in which prediction is carried out represents an appealing feature of the Bayesian inferential framework. In fact, the posterior predictive distribution allows to perform the prediction of a potentially unknown future observation of the outcome, here labeled as $\left( {\tilde{y}}^\mathrm{H},{\tilde{y}}^\mathrm{A}\right)$ and ${\tilde{z}}$. For example, considering the difference response variable ${{\varvec{z}}}$, and indicating with $\varvec{\theta }$ the vector containing all the model parameters, the posterior predictive distribution of ${\tilde{z}}$ is defined by the following integral:

$$\begin{aligned} p({\tilde{z}}|{{\varvec{z}}})=\int _{\varvec{\varTheta }}p\left( {\tilde{z}}|\varvec{\theta }\right) p(\varvec{\theta }|{\varvec{z}})\mathrm {d}\varvec{\theta }, \end{aligned}$$

where $p\left( {\tilde{z}}|\varvec{\theta }\right)$ is the likelihood function of the predicted observation and $p(\varvec{\theta }|{{\varvec{z}}})$ is the posterior distribution of the model parameters.

The posterior predictive distribution is obtained integrating out the model parameters, and therefore the predictions include all the uncertainty due to the estimation procedure. Moreover, since the MCMC samples from the posterior of $\varvec{\theta }$ are available, sampling from $p({\tilde{z}}|{{\varvec{z}}})$ is trivial. This distribution can be exploited both for forecasting purposes and for checking the model goodness-of-fit through the posterior predictive checks (Rubin 1984).

The samples generated from the posterior predictive distribution of the scored goals can be further combined to obtain the prediction of the multinomial game outcome $O_g\in \left\{ 1,X,2\right\}$. More in detail, the posterior probabilities of the outcomes of the g-th match ($p_{1g},p_{Xg},p_{2g},$) are computed, then the predicted result by the model is fixed as ${\hat{O}}_{g}=\max _{i=\left\{ 1,X,2\right\} }p_{ig}$.

As synthetic measures of the models’ ability in capturing the final result of a match, we used the correct classification rate (CC) both computed for the G in-sample units ($\hbox {CC}_\mathrm{{in}}$) and for the $G^{test}$ matches belonging to an out-of-sample set ($\text {CC}_\mathrm{{out}}$):

$$\begin{aligned} \text {CC}_\mathrm{{in}}=\frac{\sum _{g=1}^{G}{\varvec{1}}_{\left\{ O_g={\hat{O}}_g\right\} }}{G},\quad \text {CC}_\mathrm{{out}}=\frac{\sum _{g=1}^{{G}^\mathrm{test}}{\varvec{1}}_{\left\{ O_g={\hat{O}}_g\right\} }}{G^\mathrm{test}} \end{aligned}$$

and the Brier (1950) score (BS), a popular goodness-of-fit measure for categorical outcomes:

$$\begin{aligned} \text {BS}=\frac{\sum _{g=1}^{G}\sum _{i=\left\{ 1,X,2\right\} }\left( p_{ig}-{\varvec{1}}_{\left\{ O_g=i\right\} }\right) ^2}{G}. \end{aligned}$$

Note that ${\varvec{1}}_{\left\{ E\right\} }$ is an indicator function that assumes value 1 when the event E occurs and 0 otherwise.

Lastly, to compare models with the same response variable, information criteria aimed at estimating the point-wise out-of-sample model prediction accuracy are widely used in Bayesian inference. According to Vehtari et al. (2017), an efficient way to estimate this quantity is through the approximate leave-one-out cross-validation information criterion using Pareto-smoothed importance sampling (LOOIC-PSIS). Its computation is implemented in the R package loo (Vehtari et al. 2017), and the best model is the one with the smallest LOOIC value.

4 Analysis of UEFA champions league data

The models described in Sect. 3 have been applied to real data regarding the 2016-2017 UCL, including variables described in Sect. 2 as covariates. Data were collected using freely available press kits from the official UEFA website¹. They include 125 matches and 250 passing networks for the $T=32$ most competitive European teams. We point out that UCL is constituted by two phases:

• Group stage: it consists of 8 groups composed of 4 teams (6 matches per team, 12 matches per group) for a total of 96 matches;

• Knockout phase: it is composed of Round of 16, Round of 8, Semi-Finals, and Final, for a total of 29 matches. Note that the final is the only one-off match.

Fig. 2

Correlation Matrix of the explanatory variables based on Spearman’s correlation coefficient

The empirical relationships among the selected variables are firstly investigated. Figure 2 summarizes the correlations between couples of quantitative variables measured through the Spearman’s coefficient. From this figure, regarding the in-match covariates, we can notice that shots on target, ball possession, and corners show a positive correlation between them (all values exceed 0.4). On the contrary, distance and fouls suffered seem not to show any monotonic relationship with other in-match variables. Considering network summary measures, network intensity expresses a high positive correlation with both pass accuracy (0.8) and ball possession (0.6), while reciprocity is also positively correlated with all network summary measures, presenting high correlation values (greater than 0.6) with ball possession, network intensity, and pass accuracy. The diameter also shows remarkable positive correlations with ball possession, network intensity, and pass accuracy, whereas fouls suffered and distance are generally uncorrelated to overall network summary measures. Thus, we can conclude that quantities regarding physical activities and contacts between players are not mutually related to the precision of offensive actions and the level of passing interactions. Q$_3$-Hub also presents weak correlations with all variables.

Bayesian models described in Sect. 3 are fitted to the considered data using the two types of football outcomes, i.e., the scored goals $\left( y_g^\mathrm{H},y_g^\mathrm{A}\right)$ and the difference in goals ($z_g$). As mentioned, we use IP and BP models on the scored goals and the Sk model for the difference in goals, considering four different specifications of the linear predictors for each model previously presented in Subsection 3.2 and summarized in Table 3. The specification of the horseshoe prior introduced in Sect. 3.1 is completed choosing $\nu _\mathrm{slab}=7$ and $s_\mathrm{slab}=2.5$. The prior number of relevant effects $p_0$ was fixed equal to 3, using the information from a preliminary analysis using the Bayesian LASSO (Park and Casella 2008). Posterior inference is carried out on 12000 MCMC replicates that are obtained from 4 parallel chains using 6000 iterations for each. The first 3000 iterations of each chain are discarded as a warm-up period.

The convergence of the MCMC algorithm is carefully checked by visual inspection, monitoring the posterior effective sample sizes, and computing the Gelman-Rubin statistic. We remark that a tutorial concerning the estimation of considered models on our data is provided as supplementary material.

To assess the reliability of our analysis, we check the fitted models’ performance both inside and outside the sample: matches coming from the group stage ($G=96$) are used as the training set, the remaining $G^\mathrm{test}=29$ (knockout phase) ones constitute the test set. Although prediction is not our primary aim, this splitting procedure is useful to understand the consistency of the statistical relationships between the outcome and the set of covariates captured by the model.

Table 4 Goodness-of-fit measures for the three Bayesian hierarchical models according to four different covariates specifications

Table 4 shows the performances of three different models according to the four goodness-of-fit indicators (LOOIC, $\text {CC}_{\text {in}}$, $\text {CC}_{\text {out}}$, and BS) presented in Subsection 3.3. We remark that a proper comparison between all the three models can not be carried out through the LOOIC value, since Sk is specified on a different response variable with respect to IP and BP.

As expected, the addition of covariates improves all the performance indicators for each model, confirming the usefulness of the available variables set. This can be immediately checked by observing the decreasing of LOOIC values from $M_{0}$ to other linear predictors specifications. Considering also the corresponding standard error (S.E.), the IP and BP models have remarkably lower LOOIC values with formulations $M_2$ and $M_3$. On the other hand, $\mathrm{Sk}_1$ and $\mathrm{Sk}_3$ appears preferable with respect to $\mathrm{Sk}_0$ and $\mathrm{Sk}_2$. Comparing the three regression models in terms of predictive abilities of the match outcome, the best CC$_{\text {in}}$ can be found for models $\mathrm{Sk}_{2}$ and $\mathrm{Sk}_{3}$, noting that the Sk model with auxiliary information dominates IP and BP models in the CC$_{\text {in}}$ values. On the other hand, the CC$_{\text {out}}$ indicator is higher in models with Poisson likelihoods. The mismatch between CC$_{\text {in}}$ and CC$_{\text {out}}$ values for some models can be due to UCL-specific features. In fact, a class imbalance between training and test set is observed: the draw occurrence in the knockout phase is largely lower than in the group stage (10.3% vs. 31.3%).

This comparison helps to understand which specification of the linear predictor is preferable. We decided to select one model for each football outcome, in order to clarify the implications of proposed statistical analysis on football. Since the addition of a correlation term in BP models seems not to improve their performances, $\hbox {IP}_3$ is chosen to model the team scored goals, preferring its parsimony compared to $\hbox {IP}_2$. On the other hand, $\mathrm{Sk}_3$ is selected as model for the goals difference outcome, since it performs similarly to $\mathrm{Sk}_1$, but the interpretation of the coefficients is more intuitive.

After selecting the final models, we focus on their ability to fit the data exploiting the replicated datasets generated from the posterior predictive distributions and summarizing the results with the tools provided by the bayesplot package (Gabry and Mahr 2021). In the plots of Fig. 3, histograms and the 90% uncertainty intervals, centered on the median related to the simulated datasets under models $\mathrm{Sk}_3$ and $\hbox {IP}_3$, are reported. The top line refers to the distributions of goals scored by home and away teams, whereas the bottom line concerns the goals difference sample distribution. We highlight that in the case of the Skellam model, the goals distributions are generated assuming independent Poisson distributions.

The skewness of the goals difference distribution emerges from Fig. 3: the winning of home teams is usually larger compared to the away teams winning. Considering this outcome, the $\hbox{Sk}_3$ model shows its good performance in predicting the draw (i.e., a difference in goals equal to zero), while the $\hbox {IP}_3$ model tends to underestimate the probability that draws occur. This is a known feature of such models, and a possible way to face this issue is to introduce a further correlation structure in the goal-based models to inflate the draw probability (Dixon and Coles 1997; Rue and Salvesen 2000). On the other hand, observing plots in the top line, we deduce that models based on the Skellam distribution achieve the results overestimating the event of a zero goal scored by a team.

Fig. 3

Comparison of empirical data (histograms) with the posterior predictive distributions. The bold lines represent the 90% uncertainty intervals of counts around the medians

Table 5 summarizes the results of the two selected models in terms of posterior means and 90% credible intervals (C.I.) for their parameters and the regression coefficients, remarking that standardized covariates are included in the model. Focusing on the determinants of football outcome, we consider the posterior probability that a coefficient is higher or lower than 0 as a measure of importance for the covariate. In particular, shots on target is the most relevant variable for both models, showing a large positive effect on both scored goals and goals difference. Surprisingly, corners are also relevant, but show a negative impact on the two outcomes (${\mathbb {P}}\left[ \beta _2<0|{\varvec{y}}\right] =0.89$ for $\hbox {IP}_3$ and ${\mathbb {P}}\left[ \beta _2<0|{\varvec{z}}\right] =0.95$ for $\mathrm{Sk}_3$). The third variable appearing relevant in $\mathrm{IP}_3$ is the network intensity (${\mathbb {P}}\left[ \beta _6>0|{{\varvec{y}}}\right] =0.87$). Then, focusing on $\mathrm{Sk}_3$, the ball possession has a positive impact on the outcome (${\mathbb {P}}\left[ \beta _3>0|{\varvec{z}}\right] =0.90$), whereas the corresponding coefficient is shrunk toward 0 for $\mathrm{IP}_3$. Lastly, in $\mathrm{Sk}_3$, a negative coefficient can be found for the MANN indicator (${\mathbb {P}}\left[ \beta _{10}<0|{{\varvec{z}}}\right] =0.86$). Observing the remaining estimated coefficients, the other covariates share a lower relevance in explaining the football outcomes.

To conclude, we highlight that $\hbox {IP}_3$ is also characterized by lower values for the random effects scales (both for attack and defense) and home effect parameter h.

Table 5 Posterior means and $90\%$ credible intervals (C.I.) for models parameters

5 Discussion

In this section we propose a football oriented interpretation of the previous results. In particular, Subsection 5.1 aims at investigating the meaning of the fitted models, whereas Subsection 5.2 extrapolates useful indications starting from the estimated model coefficients.

5.1 Lessons from empirical models

In the previous section, we reported the general results of the two selected models. Here, we point out some features emerging from the comparison between different fitted models, discussing how covariates and model specifications impact in this applied field.

Let us consider the features of the analyzed linear predictors. Some useful empirical indications about model formulations can be deduced from the results contained in Table 4. From a predictive point of view, the outcomes of the model with covariates are comparable, but LOOIC suggests that the best trade-off between accuracy and parsimony is $M_3$. Therefore, when the outcome $(y_g^\mathrm{H},y_g^\mathrm{A})$ is analyzed, the usage of specific team covariates is preferable. On the other hand, possible differences on the pitch between the home and the away teams are conveyed through the covariate information, hence the parsimony induced by the use of the same vector $\varvec{\beta }$ is favored. In parallel, the correlation term in equation (4), introduced with the bivariate Poisson distribution, does not apparently improve the model performance in fitting our data.

Fig. 4

Comparisons of the attack random effects $\varvec{\alpha }$ and defense random effects $\varvec{\delta }$ under models $\hbox {IP}_0$ and $\hbox {IP}_3$

Our results suggest that the Skellam model represents an interesting trade-off between the result-based models and the pure goal-based ones. It takes into account the gap in terms of scored goals, avoiding to discard possible information available on the pitch, as happens in multinomial models for the final match result. Additionally, the fact that the draw constitutes a value of the response variable leads to higher performance in prediction. Despite the good in-sample behavior of Sk models, they are sensitive to the changes in the results distribution occurring between the group stage and the knock-out phase (see, e.g., the out-of-sample indicators).

Regarding the role of covariates, interesting hints can be deduced from Fig. 4, in which the posterior means of the random effects under models IP$_0$ and IP$_3$ are compared. We note that the auxiliary information is able to explain a large portion of data variability, that in the case of model IP$_0$ is absorbed by the random effects $\varvec{\alpha }$ and $\varvec{\delta }$ ($\sigma _\alpha =0.402$ and $\sigma _\delta =0.424$ under IP$_0$; $\sigma _\alpha =0.111$ and $\sigma _\delta =0.081$ under IP$_3$). This feature is encouraging for several reasons. Firstly, the fitted model appears to be correctly specified and the fixed effects well capture the scored goals behavior. Secondly, the included explanatory variables indirectly incorporate also the defensive ability of the opponent team. In addition, also the home effect h tends to be less important in models with covariates: its posterior mean under IP$_0$ is 0.391 (90% C.I.: [0.191; 0.593]), compared to 0.186 for IP$_3$ (90% C.I.: $[-0.028;0.400]$). The fact that shots on target result the most relevant covariate can be analyzed recalling that they represent necessary events in order to score a goal. For this reason, it might be interesting to develop a modeling framework in which this information is included as an offset in a Poisson regression, to study how the remaining in-match covariates and network-based measures influence the relative risk of scoring a goal.

5.2 Implications in football

Undoubtedly results from statistical models can be affected by the peculiarities and rules of the analyzed football tournament. Throughout UCL, away goals are very relevant because of the “double value” rule, possibly helping a team to progress beyond the group stage or move forward in the knockout phase. As evidence of this, 40% of goals are scored by the away teams along the whole competition. In the group stage, draws are frequent (31%) and the away team wins are not rare (29%). In the knockout phase, a change in the distribution of the results is observed: home team wins is the dominant outcome (64.3%), and fewer draws occur (10.7%).

The precision of offensive actions is crucial to score goals, or score more goals than the opponent. A competitive European team has the burden of finding and buying players able to become very accurate in shooting, i.e., with an high propensity to score goals. According to our data, the winning home teams present a median of 7 shots on target, while this number decreases to 5 if we consider the away teams able to win. Therefore, home and away teams share the same median in terms of shots on target (equal to 3) when they lose the match. This finding is crucial considering that in UCL data the ratio of scored goals over shots on target is equal to 33.4%, where the home teams are slightly more precise than the away ones (36% vs. 31%).

More surprisingly, our results show that collecting corner kicks may have a negative impact on the football outcome. Although it is not easy to give a unique interpretation for this finding, the corner kicks can be viewed as a result of the offensive actions and are positively correlated with the shots on target (see, e.g., Fig. 2). Moreover, a corner kick can be caused both by an error in shot of a forward or by an effective defensive behavior of the opposing team (e.g., a good save by the goalkeeper or a defensive stop), avoiding the goal. In addition, following this second point of view, the collection of too many corners can be harmful and may negatively affect the effectiveness of the offensive actions. Not all teams have the characteristics to take advantage from this particular game situation and, consequently, to earn additional shots on goal. To give an example, in the four matches with the highest difference in corners between home and away teams, the home one lost by a narrow margin or draw. The number of corners is not correlated (in terms of Spearman’s coefficient) with the number of goals.

The importance of network intensity suggests that a competitive team should include, in its roster, players capable of making many passes per minute, even using more “first-time” passes. Hyballa and Te Poel (2015), in their book “Passing Drills”, emphasize the need of “fast, precise, variable, and creative passing”. This indicator is especially relevant to win the away matches: we observe that the 36 winning away teams present a median of network intensity equal to 9.2, outperforming their opponents by two passes per minute (median equal to 7.2). Conversely, in the 33 draws, the median of network intensity is slightly higher for the home teams (8.0 vs 7.6), while the winning home teams express a network intensity of 8.3 (the median of losing away teams is equal to 7.4). According to the results in Fig. 2, a team able to increase its passing speed usually expresses an high passes accuracy and dominates in terms of ball possession. The positive effect of network intensity is also stressed by an observed positive correlation with the number of goals (0.32).

Concerning the $\mathrm{Sk}_{3}$ model, ball possession has an impact on the goals difference, adding value to the positive correlation (0.38) we found between these two quantities. In addition, if the ball possession of the home team is almost 20% higher than the opponent’s one, the home team scores two goals more than the opponent, in median. Conversely, if a difference of almost 20% in ball possession is in favor of the away team, they score one goal more than the home team, in median.

6 Conclusion

In this work, we firstly explored how Bayesian hierarchical models are suitable in finding the determinants of football outcomes, using auxiliary information only available from the pitch. Exploiting the widespread computational tools that are nowadays available to fit Bayesian models, alternative model specifications are proposed and compared in order to provide useful indications regarding both in-match and network-based variables. In particular, we take advantage from the flexibility of Bayesian modeling to include auxiliary information.

To summarize the main results, the effectiveness of an offensive action is crucial to determine the football outcome, but variables such as the passing speed (number of passes in the temporal unit) can improve the propensity of scoring goals or more goals than the opponent. Potential over-fitting issues are mitigated by using the regularized horseshoe prior for the regression coefficients. This feature leads us to models with good fitting results also for observations outside the training set. In fact, the relationships between covariates and the football outcomes appear robust in terms of portability of the results, and might represent also an important tool for forecasting. To investigate this aspect, the application of these models to larger competitions, such as national leagues, might be appealing, keeping in mind the peculiarities of the competition on the fore. In these cases, a large volume of past information is available and it can be exploited to produce summary measures for covariates (such as means or medians) that can be used to forecast the result of a football match, without using covariates from the game itself. The inclusion of network summary measures will be a key point in further models, even in a predictive perspective.

In this paper, we also discuss how the structural passing network features can be informative for football teams’ staff, managers, and match analysts. Passing speed, balance in terms of passing directions, team cohesion can be reasonable determinants for the football outcome.

Possible improvements on the network measures should consider spatial information on the pitch, such as the positions of players and other events as the shots on target. For example, qualitative attributes of the connection, such as long versus short passes, measures related to the evolution of the passing structure during the match, and interactions between players of two opposite teams could also provide more information about the overall match-level performances.