New activation weight calculation and parameter optimization for extended belief rule-based system based on sensitivity analysis

Abstract

An extended belief rule-based (EBRB) system is superior to existing rule-based systems in managing several types of uncertain information and modeling complex issues effectively and efficiently. However, the accuracy and interpretability of the EBRB system still need to be enhanced by addressing the following shortcomings: the interpretability of the intermediate variables in the EBRB system should be definite and the system parameters must be effectively determined. Therefore, we distinguish discrete and continuous data types to perform sensitivity analysis twice: first, on the rule inference scheme to study the interpretability of individual matching degrees and activation weights; and second, on the rule generation scheme to examine the effect of utility values and attribute weights on the accuracy of the EBRB system. Based on the analyses, we propose a novel activation weight calculation method and parameter optimization method to enhance the interpretability and accuracy of the EBRB system, respectively. We then present three case studies to elucidate the effectiveness of the proposed methods. The results indicate that the enhanced EBRB system prevents counterintuitive and insensitive situations and obtains better accuracies than some studies.

Appendices

Appendix A. Formula derivation of activation weights

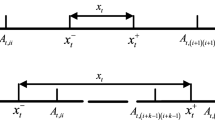
Assuming that three utility values used for the ith antecedent attribute are shown in Eq. (23), x_k,i is the sample input data to generate the kth extended belief rule, and x_i is the test input data to activate extended belief rules. Hence, when one antecedent attribute is in extended belief rules, the belief distribution of x_k,i and x_i can be simplified as follows:

For the sample input data x_k,i, the following belief distributions are obtained:

$$ S(x_{k,i} ) = \left\{ {(A_{i,j} ,\alpha_{i,j}^{k} );\;j = 1, \ldots ,J_{i} } \right\} = \left\{ {\begin{array}{*{20}l} {\left\{ {\left( {A_{i,1} ,1 - \frac{{x_{k,i} }}{{u(A_{i,2} )}}} \right),\left( {A_{i,2} ,\;\frac{{x_{k,i} }}{{u(A_{i,2} )}}} \right),(A_{i,3} ,0)} \right\};} \hfill & {{\text{if}}\;0 \le x_{k,i} \le u(A_{i,2} )} \hfill \\ {\left\{ {(A_{i,1} ,0),\left( {A_{i,2} ,\frac{{1 - x_{k,i} }}{{1 - u(A_{i,2} )}}} \right),\left( {A_{i,3} ,\frac{{x_{k,i} - u(A_{i,2} )}}{{1 - u(A_{i,2} )}}} \right)} \right\};} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.. $$

(A1)

For the test input data x_i, the following belief distributions are obtained:

$$\begin{aligned} S(x_{i} ) &= \{ (A_{i,j} ,\gamma_{i,j} );\\j &= 1, \ldots ,J_{i} \}\\ &= \left\{ {\begin{array}{*{20}l} {\{ (A_{i,1} ,1 - x_{i} ),(A_{i,2} ,1 - u(A_{i,2} ) + x_{i} ),(A_{i,3} ,x_{i} )\} ;} \hfill & {{\text{if}}\;0 \le x_{i} \le u(A_{i,2} )} \hfill \\ {\{ (A_{i,1} ,1 - x_{i} ),(A_{i,2} ,1 + u(A_{i,2} ) - x_{i} ),(A_{i,3} ,x_{i} )\} ;} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right..\end{aligned} $$

(A2)

Next, based on Eqs. (A1) and (A2), the activation weight can be grouped into four situations.

• 1. When u(A_i,1) $\le$x_k,i$\le$u(A_i,2) and u(A_i,1)$\le$x_i$\le$u(A_i,2), the activation weight is:

  $$ \begin{aligned} w_{k} & = \theta_{k} \left( {\sum\limits_{j = 1}^{Ji} {\gamma_{i,j} \alpha_{i,j}^{k} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {\left( {1 - \frac{{x_{k,i} }}{{u(A_{i,2} )}}} \right) \cdot \left( {1 - x_{i} } \right) + \frac{{x_{k,i} }}{{u(A_{i,2} )}} \cdot \left( {1 - u(A_{i,2} ) + x_{i} } \right) + 0 \cdot x_{i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {1 - \frac{{x_{k,i} }}{{u(A_{i,2} )}} - x_{i} + \frac{{x_{i} x_{k,i} }}{{u(A_{i,2} )}} + \frac{{x_{k,i} }}{{u(A_{i,2} )}} - x_{k,i} + \frac{{x_{i} x_{k,i} }}{{u(A_{i,2} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {1 - x_{i} - x_{k,i} + \frac{{2x_{i} x_{k,i} }}{{u(A_{i,2} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} . \\ \end{aligned} $$

  (A3)

• 2. When u(A_i,1) $\le$x_k,i$\le$u(A_i,2) and u(A_i,2) <  x_i$\le$u(A_i,3), the activation weight is:

  $$ \begin{aligned} w_{k} & = \theta_{k} \left( {\sum\limits_{j = 1}^{Ji} {\gamma_{i,j} \alpha_{i,j}^{k} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {\left( {1 - \frac{{x_{k,i} }}{{u(A_{i,2} )}}} \right) \cdot \left( {1 - x_{i} } \right) + \frac{{x_{k,i} }}{{u(A_{i,2} )}} \cdot \left( {1 + u(A_{i,2} ) - x_{i} } \right) + 0 \cdot x_{i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {1 - \frac{{x_{k,i} }}{{u(A_{i,2} )}} - x_{i} + \frac{{x_{i} x_{k,i} }}{{u(A_{i,2} )}} + \frac{{x_{k,i} }}{{u(A_{i,2} )}} + x_{k,i} - \frac{{x_{i} x_{k,i} }}{{u(A_{i,2} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {1 - x_{i} + x_{k,i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} . \\ \end{aligned} $$

  (A4)

• 3. When u(A_i,2) <  x_k,i$\le$u(A_i,3) and u(A_i,1) $\le$x_i$\le$u(A_i,2), the activation weight is:

  $$ \begin{aligned} w_{k} & = \theta_{k} \left( {\sum\limits_{j = 1}^{Ji} {\gamma_{i,j} \alpha_{i,j}^{k} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {0 \cdot \left( {1 - x_{i} } \right) + \frac{{1 - x_{k,i} }}{{1 - u(A_{i,2} )}} \cdot \left( {1 - u(A_{i,2} ) + x_{i} } \right) + \frac{{x_{k,i} - u(A_{i,2} )}}{{1 - u(A_{i,2} )}} \cdot x_{i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {\frac{{1 - x_{k,i} - u(A_{i,2} ) + x_{k,i} u(A_{i,2} ) + x_{i} - x_{k,i} x_{i} + x_{k,i} x_{i} - u(A_{i,2} )x_{i} }}{{1 - u(A_{i,2} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {1 + x_{i} - x_{k,i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} . \\ \end{aligned} $$

  (A5)

• 4. When u(A_i,2) <  x_k,i$\le$u(A_i,3) and u(A_i,2) <  x_i$\le$u(A_i,3), the activation weight is:

  $$ \begin{aligned} w_{k} & = \theta_{k} \left( {\sum\limits_{j = 1}^{Ji} {\gamma_{i,j} \alpha_{i,j}^{k} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {0 \cdot \left( {1 - x_{i} } \right) + \frac{{1 - x_{k,i} }}{{1 - u(A_{i,2} )}} \cdot \left( {1 + u(A_{i,2} ) - x_{i} } \right) + \frac{{x_{k,i} - u(A_{i,2} )}}{{1 - u(A_{i,2} )}} \cdot x_{i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {\frac{{1 - x_{k,i} + u(A_{i,2} ) - x_{k,i} u(A_{i,2} ) - x_{i} + x_{k,i} x_{i} + x_{k,i} x_{i} - u(A_{i,2} )x_{i} }}{{1 - u(A_{i,2} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} \\ & = \theta_{k} \left( {1 + x_{k,i} + x_{i} + \frac{{2x_{i} x_{k,i} - 2x_{k,i} - 2x_{i} }}{{1 - u(A_{i,2} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\delta_{i} }}} \right. \kern-0pt} {\delta_{i} }}}} . \\ \end{aligned} $$

  (A6)

Appendix B. Formula derivation of integrated belief degrees

Assuming that three utility values used for the consequent attribute are shown in Eq. (25), y_k is the sample output data to generate the kth extended belief rule, and y_l is the sample output data to generate the lth extended belief rule. Hence, based on the ER algorithm, the integrated belief degree without normalization is expressed as follows:

$$ \begin{aligned} \beta_{n} & = \prod\limits_{k = 1}^{2} {\left( {w_{k} \beta_{n}^{k} + 1 - w_{k} \sum\nolimits_{i = 1}^{N} {\beta_{i}^{k} } } \right)} - \prod\limits_{k = 1}^{2} {\left( {1 - w_{k} \sum\nolimits_{i = 1}^{N} {\beta_{i}^{k} } } \right)} \\ & = \left( {w_{k} \beta_{n}^{k} + 1 - w_{k} } \right)\left( {w_{l} \beta_{n}^{l} + 1 - w_{l} } \right) - \left( {1 - w_{k} } \right)\left( {1 - w_{l} } \right) \\ & = \left( {w_{k} \beta_{n}^{k} + w_{l} } \right)\left( {w_{l} \beta_{n}^{l} + w_{k} } \right) - w_{l} w_{k} \\ & = w_{k} w_{l} \beta_{n}^{k} \beta_{n}^{l} + w_{k} w_{k} \beta_{n}^{k} + w_{l} w_{l} \beta_{n}^{l} + w_{l} w_{k} - w_{l} w_{k} \\ & = w_{k} w_{l} \beta_{n}^{k} \beta_{n}^{l} + w_{k} w_{k} \beta_{n}^{k} + w_{l} w_{l} \beta_{n}^{l} . \\ \end{aligned} $$

(B1)

In addition, for the sample output data y_k, the following belief distributions are obtained:

$$\begin{aligned} S(y_{k} ) &= \{ (D_{n} ,\beta_{n}^{k} );\\ &n = 1, \ldots ,N\}\\& = \left\{ {\begin{array}{*{20}l} {\left\{ {\left( {D_{1} ,1 - \frac{{y_{k} }}{{u(D_{2} )}}} \right),\left( {D_{1} ,\frac{{y_{k} }}{{u(D_{2} )}}} \right),(D_{1} ,0)} \right\};} \hfill & {{\text{if}}\;0 \le y_{k} \le u(D_{2} )} \hfill \\ {\left\{ {(D_{1} ,0),\left( {D_{1} ,\frac{{1 - y_{k} }}{{1 - u(D_{2} )}}} \right),\left( {D_{1} ,\frac{{y_{k} - u(D_{2} )}}{{1 - u(D_{2} )}}} \right)} \right\};} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right..\end{aligned} $$

(B2)

Hence, based on Eqs. (B1) and (B2), the integrated belief degree can be grouped into four situations.

• 1. When u(D₁)$\le$y_k$\le$u(D₂) and u(D₁)$\le$y_l$\le$u(D₂), the integrated belief degree of D₂ is:

  $$ \begin{aligned} \beta_{2} & = w_{k} w_{l} \beta_{2}^{k} \beta_{2}^{l} + w_{k} w_{k} \beta_{2}^{k} + w_{l} w_{l} \beta_{2}^{l} \\ & = w_{k} w_{l} \frac{{y_{k} y_{l} }}{{u(D_{2} )u(D_{2} )}} + w_{k} w_{k} \frac{{y_{k} }}{{u(D_{2} )}} + w_{l} w_{l} \frac{{y_{l} }}{{u(D_{2} )}} \\ & = \frac{{w_{k} w_{l} y_{k} y_{l} }}{{\left( {u(D_{2} )} \right)^{2} }} + \frac{{(w_{k} )^{2} y_{k} + (w_{l} )^{2} y_{l} }}{{u(D_{2} )}}. \\ \end{aligned} $$

  (B3)

• 2. When u(D₁)$\le$y_k$\le$u(D₂) and u(D₂) < y_l$\le$u(D₃), the integrated belief degree of D₂ is:

  $$ \begin{aligned} \beta_{2} & = w_{k} w_{l} \beta_{2}^{k} \beta_{2}^{l} + w_{k} w_{k} \beta_{2}^{k} + w_{l} w_{l} \beta_{2}^{l} \\ & = w_{k} w_{l} \frac{{y_{k} (1 - y_{l} )}}{{u(D_{2} )\left( {1 - u(D_{2} )} \right)}} + w_{k} w_{k} \frac{{y_{k} }}{{u(D_{2} )}} + w_{l} w_{l} \frac{{1 - y_{l} }}{{1 - u(D_{2} )}} \\ & = \frac{{w_{k} w_{l} y_{k} (1 - y_{l} )}}{{u(D_{2} )\left( {1 - u(D_{2} )} \right)}} + \frac{{(w_{k} )^{2} y_{k} }}{{u(D_{2} )}} + \frac{{(w_{l} )^{2} (1 - y_{l} )}}{{1 - u(D_{2} )}}. \\ \end{aligned} $$

  (B4)

• 3. When u(D₂) < y_k$\le$u(D₃) and u(D₁)$\le$y_l$\le$u(D₂), the integrated belief degree of D₂ is:

  $$ \begin{aligned} \beta_{2} & = w_{k} w_{l} \beta_{2}^{k} \beta_{2}^{l} + w_{k} w_{k} \beta_{2}^{k} + w_{l} w_{l} \beta_{2}^{l} \\ & = w_{k} w_{l} \frac{{(1 - y_{k} )y_{l} }}{{\left( {1 - u(D_{2} )} \right)u(D_{2} )}} + w_{k} w_{k} \frac{{1 - y_{k} }}{{1 - u(D_{2} )}} + w_{l} w_{l} \frac{{y_{l} }}{{u(D_{2} )}} \\ & = \frac{{w_{k} w_{l} (1 - y_{k} )y_{l} }}{{\left( {1 - u(D_{2} )} \right)u(D_{2} )}} + \frac{{(w_{k} )^{2} (1 - y_{k} )}}{{1 - u(D_{2} )}} + \frac{{(w_{l} )^{2} y_{l} }}{{u(D_{2} )}}. \\ \end{aligned} $$

  (B5)

• 4. When u(D₂) < y_k$\le$u(D₃) and u(D₂) < y_l$\le$u(D₃), the integrated belief degree of D₂ is:

  $$ \begin{aligned} \beta_{2} & = w_{k} w_{l} \beta_{2}^{k} \beta_{2}^{l} + w_{k} w_{k} \beta_{2}^{k} + w_{l} w_{l} \beta_{2}^{l} \\ & = w_{k} w_{l} \frac{{(1 - y_{k} )(1 - y_{l} )}}{{\left( {1 - u(D_{2} )} \right)\left( {1 - u(D_{2} )} \right)}} + w_{k} w_{k} \frac{{1 - y_{k} }}{{1 - u(D_{2} )}} + w_{l} w_{l} \frac{{1 - y_{l} }}{{1 - u(D_{2} )}} \\ & = \frac{{w_{k} w_{l} (1 - y_{k} )(1 - y_{l} )}}{{\left( {1 - u(D_{2} )} \right)^{2} }} + \frac{{(w_{k} )^{2} (1 - y_{k} ) + (w_{l} )^{2} (1 - y_{l} )}}{{1 - u(D_{2} )}}. \\ \end{aligned} $$

  (B6)