Skip to main content
Springer Nature Link
Log in

Operational local join count statistics for cluster detection

  • Original Article
  • Published:
Journal of Geographical Systems Aims and scope Submit manuscript

Abstract

This paper operationalizes the idea of a local indicator of spatial association for the situation where the variables of interest are binary. This yields a conditional version of a local join count statistic. The statistic is extended to a bivariate and multivariate context, with an explicit treatment of co-location. The approach provides an alternative to point pattern-based statistics for situations where all potential locations of an event are available (e.g., all parcels in a city). The statistics are implemented in the open-source GeoDa software and yield maps of local clusters of binary variables, as well as co-location clusters of two (or more) binary variables. Empirical illustrations investigate local clusters of house sales in Detroit in 2013 and 2014, and urban design characteristics of Chicago census blocks in 2017.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Notes

  1. For a general discussion of spatial weights, see, for example, Bavaud (1998), Getis (2009), and Anselin and Rey (2014). Social interaction and social network extensions can be found in Dow et al. (1982), Akerlof (1997), Leenders (2002), Páez et al. (2008), and Papachristos and Bartomski (2018), among others.

  2. In some rare examples, data on the complete population are available, and a case-control design becomes equivalent to a lattice data setting. However, in a typical case-control setup, the controls are a sample, and thus, not all non-event locations are included.

  3. Rogerson (2006) also includes a local form of the statistic, which counts the number of cases among the neighbors for a given location. Except for the case-control setup, this is formally equivalent to the local join count statistic described below.

  4. This is formally the same as the Jacquez et al. (2005) local Q statistic for location i at time t with k-nearest neighbors, i.e., \(Q_{i,k,t} = c_i \sum _j n_{ijkt} c_j\), where \(c_{i,j} = 1\) for a case and \(= 0\) for a control, and \(n_{ijkt}\) are the nearest neighbor weights for k-nearest neighbors of location i at time t. It is also essentially the same as the local similarity relation in Farber et al. (2015), i.e., \(\Gamma _{d,i} = \sum _j I_{ij}\), where \(I_{ij} = 1\) when the values at i and j are “similar” for d nearest neighbors. In contrast to these measures, which are based on nearest neighbor relations, the local join count statistic is couched in a lattice data structure with spatial weights. Formally, the expressions are the same, but conceptually, they differ.

  5. Yet a different strand of local cluster statistics is based on the scan-statistic logic first outlined in Kulldorff (1997), and its many extensions. However, since this approach does not provide a link between a local and global statistic—a fundamental property of a LISA statistic as outlined in Anselin (1995)—it is not further considered here.

  6. Note that this is a conditional probability. It thus underestimates the actual uncertainty associated with the occurrence of a value of 1 and its particular configuration of neighbors. The unconditional probability would be the joint probability of observing \(x_i = 1\)andp neighbors \(x_j = 1\). This not what is considered here.

  7. In larger samples, the distinction between using \(N-1\) and \(P-1\) compared to N and P is likely negligible. Also, the distinction between sampling without replacement (the hypergeometric distribution) and sampling with replacement (the binomial distribution) is likely to be small for large data sets with few events.

  8. This is the logic behind the local z statistic for the case-control setting suggested in Rogerson (2006).

  9. In the limit, the neighbors would include all other observations.

  10. Note how a case-control setup can be couched in these terms, since a case and a control cannot occur at the same location. For example, \(x_i = 1\) for a case and \(z_j = 1\) for a control. The BJC statistic would then count the number of controls among the neighbors of i, or, with the roles reversed, the number of cases around a control a i.

  11. Since the conditional permutation is designed to draw tuples of existing pairs of x and z, the procedure respects the in-place association between x and z.

  12. Formally, we could also consider the situation where \(x_i = z_i = 1\) is surrounded by either \(z_j = 1\) or \(x_j = 1\), ignoring the value for the other variable. However, we see little practical application where there is a meaningful interpretation for this situation, and we do not consider it further.

  13. Repeat sales were removed from the data set (only the latest sale is recorded), so that there is no overlap between the two point patterns.

  14. Note that not all sales are standard transactions and many are the result of auctions, resulting in arbitrary sales prices, typically less than $1000. We ignore the actual sales value in our analysis, but keep all transactions in the data set.

  15. In the point pattern approach taken by Cromley et al. (2014) and Wang et al. (2017), this would be equivalent to a uniform adaptive kernel, in the sense that each neighbor gets equal weight and each observation has exactly 30 neighbors.

  16. Because of the resolution of the map, it is not possible to distinguish all individual points, since several pertain to close-by locations that tend to be plotted on top of each other.

  17. Recall that by construction, none of the points overlap between the two years.

  18. Again, due to the scale of the map, the figure only shows eight points. In three cases, two adjoining locations are found that cannot be individually distinguished in the map.

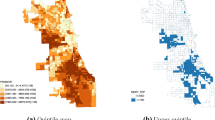
  19. The classification is derived from an extensive set of data, most notably the City of Chicago Business Licenses data for 2017. Most data are for 2017, a few are for 2016, and the sidewalk data are for 2012. The census block definition is from 2010. Details can be found in Talen and Jeong (2018, Table 1).

  20. Note that the highlighted blocks form the core of the cluster, but do not include the neighbors that also may show co-location. In this example, several blocks are neighbors as well, but this is not always the case. In other words, the highlighted blocks underestimate the spatial extent of the actual cluster.

References

  • Akerlof GA (1997) Social distance and social decisions. Econometrica 65:1005–1027

    Article  Google Scholar 

  • Anselin L (1995) Local indicators of spatial association—LISA. Geogr Anal 27:93–115

    Article  Google Scholar 

  • Anselin L (1996) The Moran scatterplot as an ESDA tool to assess local instability in spatial association. In: Fischer M, Scholten H, Unwin D (eds) Spatial analytical perspectives on GIS in environmental and socio-economic sciences. Taylor and Francis, London, pp 111–125

    Google Scholar 

  • Anselin L (2019) A local indicator of multivariate spatial association: extending Geary’s c. Geogr Anal 51:133–150. https://doi.org/10.1111/gean.12164

    Article  Google Scholar 

  • Anselin L, Rey SJ (2014) Modern spatial econometrics in practice, a guide to GeoDa, GeoDaSpace and PySAL. GeoDa Press, Chicago

    Google Scholar 

  • Anselin L, Syabri I, Smirnov O (2002) Visualizing multivariate spatial correlation with dynamically linked windows. In: Anselin L, Rey S (eds) New tools for spatial data analysis: proceedings of the specialist meeting. Center for Spatially Integrated Social Science (CSISS), University of California, Santa Barbara. CD-ROM

  • Bavaud F (1998) Models for spatial weights: a systematic look. Geogr Anal 30:153–171

    Article  Google Scholar 

  • Boots B (2003) Developing local measures of spatial association for categorical data. J Geogr Syst 5:139–160

    Article  Google Scholar 

  • Boots B (2006) Local configuration measures for categorical spatial data: binary regular lattices. J Geogr Syst 8:1–24

    Article  Google Scholar 

  • Cliff A, Ord JK (1973) Spatial autocorrelation. Pion, London

    Google Scholar 

  • Congdon P (2016) A local join counts methodology for spatial clustering in disease from relative risk models. Commun Stat Theory Methods 45:3059–3075

    Article  Google Scholar 

  • Cromley RG, Hanink DM, Bentley GC (2014) Geographically weighted colocation quotients: specification and application. Prof Geogr 66:138–148

    Article  Google Scholar 

  • Cuzick J, Edwards R (1990) Spatial clustering for inhomogeneous populations. J R Soc B 52:73–104

    Google Scholar 

  • de Castro MC, Singer BH (2006) Controlling the false discovery rate: an application to account for multiple and dependent tests in local statistics of spatial association. Geogr Anal 38:180–208

    Article  Google Scholar 

  • Dow MM, Burton ML, White DR (1982) Network autocorrelation: a simulation study of a foundational problem in regression and survey research. Soc Netw 4:169–200

    Article  Google Scholar 

  • Efron B, Hastie T (2016) Computer age statistical inference, algorithms, evidence, and data science. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Farber S, Martin MR, Páez A (2015) Testing for spatial independence using similarity relations. Geogr Anal 47:97–120

    Article  Google Scholar 

  • Getis A (1984) Interaction modeling using second-order analysis. Environ Plan A 16:173–183

    Article  Google Scholar 

  • Getis A (2009) Spatial weights matrices. Geogr Anal 41:404–410

    Article  Google Scholar 

  • Getis A, Franklin J (1987) Second-order neighborhood analysis of mapped point patterns. Ecology 68:473–477

    Article  Google Scholar 

  • Getis A, Ord JK (1992) The analysis of spatial association by use of distance statistics. Geogr Anal 24:189–206

    Article  Google Scholar 

  • Getis A, Ord JK (1996) Local spatial statistics: an overview. In: Longley P, Batty M (eds) Spatial analysis: modeling in a GIS environment. GeoInformation International, pp 261–277

  • Huang Y, Shekhar S, Xiong H (2004) Discovering colocation patterns from spatial data sets: a general approach. IEEE Trans Knowl Data Eng 16:1472–1485

    Article  Google Scholar 

  • Hubert LJ, Golledge R, Costanzo CM (1981) Generalized procedures for evaluating spatial autocorrelation. Geogr Anal 13:224–233

    Article  Google Scholar 

  • Jacquez GM, Kaufmann A, Meliker J, Goovaerts P, AvRuskin G, Nriagu J (2005) Global, local and focused geographic clustering for case-control data with residential histories. Environ Health 4:4

    Article  Google Scholar 

  • Jacquez GM, Meliker JR, AvRuskin GA, Goovaerts P, Kaufmann A, Wilson ML, Nriagu J (2006) Case-control geographic clustering for residential histories accounting for risk factors and covariates. Int J Health Geogr 5:32

    Article  Google Scholar 

  • Jirjies S, Wallstrom G, Halden RU, Scotch M (2016) pyJacqQ: python implementation of Jacquez’s Q-statistics for space-time clustering of disease exposure in case-control studies. J Stat Softw. https://doi.org/10.18637/jss.v074.i06

    Google Scholar 

  • Kulldorff M (1997) A spatial scan statistic. Commun Stat Theory Methods 26:1481–1496

    Article  Google Scholar 

  • Lee S-I (2001) Developing a bivariate spatial association measure: an integration of Pearson’s r and Moran’s I. J Geogr Syst 3:369–385

    Article  Google Scholar 

  • Leenders RTAJ (2002) Modeling social influence through network autocorrelation: constructing the weights matrix. Soc Netw 24:21–47

    Article  Google Scholar 

  • Leslie TF, Kronenfeld BJ (2011) The colocation quotient: a new measure of spatial association between categorical subsets of points. Geogr Anal 43:306–326

    Article  Google Scholar 

  • Leslie TF, Frankenfeld CL, Makara MA (2012) The spatial food environment of the DC metropolitan area: clustering, co-location, and categorical differentiation. Appl Geogr 35:300–307

    Article  Google Scholar 

  • Long JA, Nelson TA, Wulder MA (2010) Local indicators for categorical data: impacts of scaling decisions. Can Geogr/Le Géographe Canadien 54:15–28

    Article  Google Scholar 

  • López F, Matilla-García M, Mur J, Marín MR (2010) A non-parametric spatial independence test using symbolic entropy. Reg Sci Urban Econ 40:106–115

    Article  Google Scholar 

  • Mack EA, Credit K, Suandi M (2017) A comparative analysis of firm co-location behavior in the Detroit metropolitan area. Ind Innov 25:264

    Article  Google Scholar 

  • Moran PA (1948) The interpretation of statistical maps. Biometrika 35:255–260

    Google Scholar 

  • Okabe A, Boots B, Sato T (2010) A class of local and global K functions and their exact statistical properties. In: Anselin L, Rey SJ (eds) Perspectives on spatial data analysis. Springer, Berlin, pp 101–112

    Chapter  Google Scholar 

  • Ord JK, Getis A (1995) Local spatial autocorrelation statistics: distributional issues and an application. Geogr Anal 27:286–306

    Article  Google Scholar 

  • Ord JK, Getis A (2001) Testing for local spatial autocorrelation in the presence of global autocorrelation. J Reg Sci 41:411–432

    Article  Google Scholar 

  • Páez A, Scott DM, Volz E (2008) Weight matrices for social influence analysis: an investigation of measurement errors and their effect on model identification and estimation quality. Soc Netw 30:309–317

    Article  Google Scholar 

  • Papachristos AV, Bartomski S (2018) Connected in crime: the enduring effect of neighborhood networks on the spatial patterning of violence. Am J Sociol 124:517–568

    Article  Google Scholar 

  • Ripley BD (1981) Spatial statistics. Wiley, New York

    Book  Google Scholar 

  • Rogerson PA (2006) Statistical methods for the detection of spatial clustering in case-control data. Stat Med 25:811–823

    Article  Google Scholar 

  • Rogerson PA (2015) Maximum Getis-Ord statistic adjusted for spatially autocorrelated data. Geogr Anal 47:20–33

    Article  Google Scholar 

  • Ruiz M, López F, Páez A (2010) Testing for spatial association of qualitative data using symbolic dynamics. J Geogr Syst 12:281–309

    Article  Google Scholar 

  • Talen E, Jeong H (2018) Does the classic American main street still exist? An exploratory look. J Urban Des. https://doi.org/10.1080/13574809.2018.1436962

    Google Scholar 

  • Wang F, Hu Y, Wang S, Li X (2017) Local indicator of colocation quotient with a statistical significance test: examining spatial association of crime and facilities. Prof Geogr 69:22–31

    Article  Google Scholar 

Download references

Acknowledgements

This research was funded in part by Award 1R01HS021752-01A1 from the Agency for Healthcare Research and Quality (AHRQ), “Advancing spatial evaluation methods to improve healthcare efficiency and quality.” Emily Talen and Hyesun Jeong provided the urban design classifications of the Chicago census block data. Comments by Julia Koschinsky and referees on an earlier version of the paper are greatly appreciated.

Author information

Authors and Affiliations

  1. Center for Spatial Data Science, The University of Chicago, Chicago, IL, 60637, USA

    Luc Anselin & Xun Li

Authors
  1. Luc Anselin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xun Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Luc Anselin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Anselin, L., Li, X. Operational local join count statistics for cluster detection. J Geogr Syst 21, 189–210 (2019). https://doi.org/10.1007/s10109-019-00299-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10109-019-00299-x

Keywords

JEL Classification