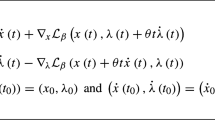Semiglobal exponential stability of the discrete-time Arrow-Hurwicz-Uzawa primal-dual algorithm for constrained optimization

Abstract

We consider the discrete-time Arrow-Hurwicz-Uzawa primal-dual algorithm, also known as the first-order Lagrangian method, for constrained optimization problems involving a smooth strongly convex cost and smooth convex constraints. We prove that, for every given compact set of initial conditions, there always exists a sufficiently small stepsize guaranteeing exponential stability of the optimal primal-dual solution of the problem with a domain of attraction including the initialization set. Inspired by the analysis of nonlinear oscillators, the stability proof is based on a non-quadratic Lyapunov function including a nonlinear cross term.

1 Introduction

1.1 Problem overview, contribution, and literature review

In this article, we study the convergence and Lyapunov stability properties of the following discrete-time first-order primal-dual algorithm

$$\begin{aligned} x^{t+1}&= x^t - \gamma \left( \nabla f(x^t)+ \sum _{i=1}^r \lambda ^t_i\nabla g_i(x^t) \right) ,{} & {} x^0\in {\mathbb {R}}^n, \end{aligned}$$

(1a)

$$\begin{aligned} \lambda ^{t+1}_i&= \max \big \{ 0,\ \lambda ^t_i+ \gamma g_i(x^t)\big \},{} & {} \lambda ^{0}_i \ge 0,{} & {} i=1,\dots ,r, \end{aligned}$$

(1b)

in which $t\in {\mathbb {N}}$ is the iteration counter, $n,r\in {\mathbb {N}}$ are arbitrary, $x^t\in {\mathbb {R}}^n$ is the primal variable, $\lambda _i^t\in {\mathbb {R}}_{\ge 0}$ are the dual variables, $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ and $g=(g_1,\dots , g_r):{\mathbb {R}}^n\rightarrow {\mathbb {R}}^r$ are convex functions, and $\gamma >0$ is a parameter called the stepsize. Algorithm (1) gives an iterative procedure to compute a solution of the constrained optimization problem

$$\begin{aligned} \begin{aligned} \displaystyle \min _{x\in {\mathbb {R}}^n} \,&\, f(x) \\ \mathrm {subj.~to} \,&\, g_i(x)\le 0,&i&=1,\dots , r, \end{aligned} \end{aligned}$$

(2)

and it is a slight variation of Uzawa’s original method [29]. In particular, when $\lambda _i^t+\gamma g_i(x^t)\ge 0$ for all $i=1,\dots ,r$, Eqs. (1) take the form of a discrete-time version of the Arrow-Hurwicz saddle-point dynamics [1] (see also [18]) applied to the Lagrangian function of (2), which reads as

$$\begin{aligned} L(x,\lambda ) {:}{=}f(x) + \sum _{i=1}^r \lambda _i g_i(x). \end{aligned}$$

Indeed, (1) can be rewritten in compact form as

$$\begin{aligned} x^{t+1}&= x^t - \gamma \frac{\partial L}{\partial x} (x^t,\lambda ^t) ,{} & {} x^0\in {\mathbb {R}}^n, \\ \lambda ^{t+1}&= \max \left\{ 0,\ \lambda ^t+ \gamma \frac{\partial L}{\partial \lambda } (x^t,\lambda ^t) \right\} ,{} & {} \lambda ^{0}\in ({\mathbb {R}}_{\ge 0})^r, \end{aligned}$$

in which the $\max$ operator acts component-wise. Hence, (1) is a first-order Lagrangian method.

In his original paper [29], Uzawa provided a proof of non-local stability and convergence of (1). However, his arguments were later found wrong (see, e.g., [25, Sec. 1]). Other existing proofs, which can be found, for instance, in [25] and the classical textbook [2], only provide local convergence guarantees to a saddle point of the Lagrangian function L. These results are based on the linear approximation of the algorithm around the optimal point (see, e.g., [2, Sec. 4.4]) and, hence, can only guarantee convergence from a (possibly very small) neighborhood of the optimum, whose size is not guaranteed to increase as the stepsize $\gamma$ decreases. Nonlocal convergence results have been obtained in [15, 16] at the cost, however, of adopting a diminishing stepsize. An extension of the latter results to a stochastic setting is studied in [30] in the context of distributed network utility maximization. Other nonlocal, yet approximate, convergence bounds have been given in [23] under the assumption of gradient boundedness. Finally, it is worth noticing that versions of (1) tailored for quadratic programs have been widely studied in the context of imaging; see, e.g., [3]. Despite the numerous results and the long history of Algorithm (1), to the best of the authors’ knowledge, a purely discrete-time analysis providing nonlocal convergence and stability guarantees is still missing.

Interestingly, guarantees of such kind do exist for the continuous-time version of Algorithm (1), which is also known as saddle-point or saddle-flow dynamics. See, for instance, references [4,5,6,7, 9, 11, 12, 26] and extensions covering the augmented Lagrangian version [28] of (1) and its proximal regularization [10]. In particular, in continuous time one can achieve global [5,6,7, 9, 11] and even exponential [4, 26] convergence in some cases, resulting in a sharp distinction between the continuous- and discrete-time domains. However, the results attained for continuous-time algorithms are typically not preserved under (Euler) discretization and, therefore, cannot be used to assess equivalent properties on their (first-order) discretization. In particular, the continuous-time algorithms cited above, for which global and/or exponential stability guarantees do exist, typically consist in differential equations defined by a vector field that is discontinuous at some relevant points. Yet, continuity is generally required to apply the basic discretization theorems (see, e.g., [27, Sects. 2.1.1 and 2.3]). Among the continuous-time algorithms employing continuous vector fields and ensuring global convergence it is worth mentioning [13, Eq. (5)] (see also [8]). However, a simple counterexample, similar to that reported later in Sect. 1.2, can be used to show that the Euler discretization of such an algorithm cannot be globally convergent. Hence, also in these cases, the continuous-time results are not directly extendable to cover the algorithms’ discretization.

In view of the above discussion, to the best of the authors’ knowledge, a nonlocal stability and convergence proof for the discrete-time algorithm (1) is still an open, long-standing problem, even under strong convexity of f and convexity of g (which we shall assume later on). In this article, we aim to fill this gap by providing a purely discrete-time semiglobal asymptotic stability analysis for (1). As shown in Sect. 1.2, global convergence is generically not possible for Algorithm (1); hence, a semiglobal result is the best one can achieve in the general case. Specific contributions are highlighted in the next section.

1.2 Contributions

Under widely adopted regularity and convexity assumptions on f and g detailed later in Sect. 2.1, we prove that the minimizer of (2) (which is unique under the assumptions of the article) is semiglobally¹ Lyapunov stable and exponentially attractive for Algorithm (1). More specifically, we show that there exists an equilibrium $(x^\star ,\lambda ^\star )\in {\mathbb {R}}^n\times {\mathbb {R}}^r$ for (1), with $x^\star$ being the optimal solution of (2) and $\lambda ^\star$ the corresponding optimal Lagrange multiplier, and that, for every arbitrary compact set $\Xi _0\subseteq {\mathbb {R}}^n\times {\mathbb {R}}^r$ of initial conditions for (1), there exists $\gamma ^\star >0$, such that, for all $\gamma \in (0,\gamma ^\star )$, the following properties hold:

• 1. Lyapunov stability: for every $\varepsilon >0$, there exists $\delta >0$, such that $|x^0-x^\star |<\delta$ and $|\lambda ^0-\lambda ^\star |<\delta$ imply $|x^t-x^\star |<\varepsilon$ and $|\lambda ^t-\lambda ^\star |<\varepsilon$ for all $t\in {\mathbb {N}}$.

• 2. Attractiveness: every solution² of (1) with $(x^0,\lambda ^0)\in \Xi _0$ satisfies $\lim _{t\rightarrow \infty }|x^t - x^\star |=0$ and $\lim _{t\rightarrow \infty }|\lambda ^t - \lambda ^\star |=0$.

• 3. Exponential (or linear) convergence: there exist $\sigma >0$ and $\mu \in (0,1)$ (depending on $\gamma$ and $\Xi _0$) such that every solution of (1) with $(x^0,\lambda ^0)\in \Xi _0$ satisfies

  $$\begin{aligned} \forall t\in {\mathbb {N}},\quad |(x^t,\lambda ^t)-(x^\star ,\lambda ^\star )| \le \sigma \mu ^t |(x^0,\lambda ^0)-(x^\star ,\lambda ^\star )|. \end{aligned}$$

The previously-defined stability notion, known as Lyapunov stability [19, 17, Ch. 4], is a continuity property of the algorithm’s trajectories with respect to variations of the initial conditions. It guarantees that small deviations of the initial conditions from the optimal point $(x^\star ,\lambda ^\star )$ do not lead to large deviations from it along the algorithm’s trajectories. We underline that Lyapunov stability, attractiveness, and exponential convergence are guaranteed from an arbitrarily large compact initialization set $\Xi _0$, provided that $\gamma$ is chosen sufficiently small. This semiglobal result is strictly stronger than its local counterpart that, indeed, would only guarantee the existence of a (possibly very small) neighborhood $\Xi _0$ of $(x^\star ,\lambda ^\star )$ from which the previous properties hold. However, it is also weaker than a global result, for which a single $\gamma$ would work for all possible initialization sets $\Xi _0$. Nevertheless, we observe that the lack of global convergence is not a shortcoming of our analysis; indeed, global convergence is, in general, not possible for (1). This can be seen by means of a simple counterexample. Take $n=r=1$, $f(x)=x^2$ and $g(x)=x^2-1$. Fix $\gamma >0$ arbitrarily. Then, every solution with initial conditions satisfying

$$\begin{aligned} x^0&\ge 2,&\lambda ^0&\ge \frac{1+\sqrt{2}}{2\gamma } \end{aligned}$$

(3)

diverges. In fact from (1), one obtains that, for all $t\in {\mathbb {N}}$,

$$\begin{aligned} \left\{ \begin{aligned} x^t&\ge 2, \\ \lambda ^t&\ge \frac{1+\sqrt{2}}{2\gamma } \end{aligned} \right. \implies \left\{ \begin{aligned} |x^{t+1}|^2&= \left( 1 - 2\gamma - 2\gamma \lambda ^t \right) ^2 |x^t|^2 \ge 2 |x^t|^2 \ge 2 , \\ \lambda ^{t+1}&= \lambda ^t + \gamma \big (|x^t|^2-1\big ) \ge \lambda ^t \ge \frac{1+\sqrt{2}}{2\gamma }. \end{aligned} \right. \end{aligned}$$

By induction, one thus obtains that (3) implies $x^t\ge 2$ and $\lambda ^t \ge \frac{1+\sqrt{2}}{2\gamma }$ for all $t\in {\mathbb {N}}$ and, moreover, that $|x^{t+1}|^2 \ge 2 |x^t|^2$ holds for all $t\in {\mathbb {N}}$. Hence, the trajectory x diverges exponentially.

1.3 A systems-theoretic approach

Local stability and convergence results based on the linear approximation of the algorithm’s equations cannot be easily extended to nonlocal results where the nonlinear terms dominate. Instead, the analysis approach pursued in this article is based on the theory of Lyapunov functions [17, Chapter 4], which is better suited to handle purely nonlinear problems like the one considered in the paper. Finding a suitable Lyapunov function is in general difficult, and a counterexample can be used to show that the simple choice $(x-x^\star )^2 + (\lambda -\lambda ^\star )^2$, used by Uzawa in the aforementioned article [29], would not work. In this direction, it helps to look at (1) from a different perspective. Namely, by ignoring the “$\max$” in the equation of $\lambda$, we can look at (1) as the Euler discretization (with sampling time $\gamma$) of the following continuous-time system (consider $r=1$ for simplicity)

$$\begin{aligned} \dot{x}&= -\nabla g(x) \lambda - \nabla f(x),\\ {\dot{\lambda }}&= g(x). \end{aligned}$$

This is the equation of a nonlinear oscillator with $\nabla g(x)$ playing the role of the natural frequency, and $-\nabla f(x)$ that of a nonlinear damping term. It is well-known [17, Example 4.4], that Lyapunov functions for nonlinear oscillators must have a cross-term. This is what ultimately motivated the specific choice for the Lyapunov function used in this article, formally defined in (25). In turn, the introduction of a suitable cross-term, which can be seen as a modification of Uzawa’s Lyapunov candidate function, turned out to be key for proving stability and convergence.

1.4 Organization and notation

Organization. In Sect. 2, we detail the basic assumptions and link the equilibria of (1) to the optimal solution of (2). In Sect. 3, we state the main result of the paper proving semiglobal exponential stability of the optimal equilibrium. Finally, the proof of the main result is presented in Sect. 4.

Notation. Set inclusion (either strict or not) is denoted by $\subseteq$. If S is a set and $\sim$ a binary relation on it, for $s\in S$ we let $S_{\sim s}{:}{=}\{ z\in S\,:\,z\sim s\}$. The closed ball of radius r centered at ${\bar{x}}\in {\mathbb {R}}^n$ is denoted by ${\overline{{\mathbb {B}}}}_{r}({\bar{x}}) {:}{=}\{x \in {\mathbb {R}}^n \,:\,|x-{\bar{x}}|\le r\}$. We identify linear operators ${\mathbb {R}}^m\rightarrow {\mathbb {R}}^n$ with their matrix representation with respect to the standard bases of ${\mathbb {R}}^m$ and ${\mathbb {R}}^n$. If $A,B\in {\mathbb {R}}^{n\times n}$, $A\ge B$ means that $A-B$ is positive semidefinite. Given a scalar function $f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}$, we define its gradient as $\nabla f(\cdot ) = (\partial f(\cdot )/\partial x_1,\ldots ,\partial f(\cdot )/\partial x_n)\in {\mathbb {R}}^{n}$. Given a vector field $g:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^r$, we let $\nabla g(\cdot ) {:}{=}\begin{bmatrix} \nabla g_1(\cdot )&\cdots&\nabla g_r(\cdot ) \end{bmatrix} \in {\mathbb {R}}^{n\times r}$. We equip ${\mathbb {R}}^n$ with the standard inner product $\langle x \,|\, y \rangle {:}{=}\sum _{i=1}^n x_i y_i$, and we denote the induced Euclidean norm by $|x|{:}{=}\sqrt{\langle x \,|\, x \rangle }$. If $x\in {\mathbb {R}}^n$ and $\sim$ is a binary relation on ${\mathbb {R}}$, $x\sim 0$ means $x_i\sim 0$ for all $i=1,\dots ,n$. Similarly, $\max \{0,x\} {:}{=}(\max \{0,x_1\},\dots , \max \{0,x_n\})$ and, for $y\in {\mathbb {R}}^n$, $\max \{y,x\} {:}{=}(\max \{y_1,x_1\},\dots , \max \{y_n,x_n\})$. For notation convenience, we write (x, y) in place of ((x, y)). For instance, ${\overline{{\mathbb {B}}}}_{r}(1,2)$ is the closed ball of radius r in ${\mathbb {R}}^2$ centered at $(1,2)\in {\mathbb {R}}^2$. We denote by $(\cdot )^+$ the “shift” operator such that, for a discrete-time signal $x:{\mathbb {N}}\rightarrow {\mathbb {R}}^n$, $x^+(t) = x(t+1)$. For brevity, in dealing with time signals, we use the notation $x^t$ in place of x(t).

2 The framework

2.1 Standing assumptions and optimality conditions

We consider Algorithm (1) and Problem (2) under the following assumptions.

Assumption 1

The functions f and $g_i$ satisfy the following properties:

• A . f is strongly convex and twice continuously differentiable;

• B . for all $i=1,\ldots ,r$, $g_i$ is convex and twice continuously differentiable;

• C . there exists ${\bar{x}} \in {\mathbb {R}}^n$ such that $g_i({\bar{x}})\le 0$ for all $i=1,\ldots ,r$.

The conditions asked by Assumption 1 are widely adopted [2]. In particular, they imply that the optimization problem (2) has a unique solution, as established by the lemma below.

Lemma 1

Suppose that Assumption 1 holds. Then, there exists a unique $x^\star \in {\mathbb {R}}^n$ solving (2).

The proof of Lemma 1 is given in the Appendix. Throughout the article, we denote by $x^\star$ the unique optimal solution of (2). Moreover, we let

$$\begin{aligned} A(x^\star ) {:}{=}\{ i\in \{1,\dots , r\}\,:\,g_i(x^\star )=0\} \end{aligned}$$

denote the set of indices of the active constraints at $x^\star$. Then, in addition to Assumption 1, we assume that $x^\star$ is a regular point in the following sense.

Assumption 2

The vectors $\{\nabla g_i(x^\star )\,:\,i\in A(x^\star )\}$ are linearly independent.

Like Assumption 1, also Assumption 2 is customary [2]. In particular, Lemma 1 (hence, Assumption 1) and Assumption 2 imply that there necessarily exists a unique $\lambda ^\star \in {\mathbb {R}}^r$ such that the so-called KKT conditions hold (see, e.g., [2, Prop. 3.3.1])

$$\begin{aligned}&\nabla f (x^\star ) + \nabla g(x^\star ) \lambda ^\star = 0 , \end{aligned}$$

(4a)

$$\begin{aligned}&g_i (x^\star ) \le 0, \quad \lambda _i^\star \ge 0, \quad \lambda _i^\star g_i(x^\star ) = 0, \quad \forall i=1,\ldots ,r. \end{aligned}$$

(4b)

Notice that Conditions (4) are also sufficient. Namely, if some $(x^\star ,\lambda ^\star )$ satisfies (4), then $x=x^\star$ is the optimal solution of (2) (see, e.g., [2, Prop. 3.3.4]).

2.2 Optimality and equilibria

Algorithm (1) can be rewritten in compact form as³

$$\begin{aligned} x^+&= x - \gamma \nabla L(x,\lambda ),{} & {} x^0\in {\mathbb {R}}^n , \end{aligned}$$

(5a)

$$\begin{aligned} \lambda ^+&= \max \big \{ 0,\ \lambda + \gamma g(x)\big \},{} & {} \lambda ^{0} \ge 0 , \end{aligned}$$

(5b)

where $L(x,\lambda ) {:}{=}f(x) + \langle \lambda \,|\, g(x) \rangle$ denotes the Lagrangian function associated with (2). We remark that the initialization $\lambda ^0\ge 0$ is only assumed to simplify the analysis and it is not necessary. Indeed, (5b) trivially implies $\lambda ^t\ge 0$ for all $t\ge 1$ even if $\lambda ^0 <0$.

The following lemma characterizes the equilibria of (5) in terms of the optimality conditions (4).

Lemma 2

$(x,\lambda )\in {\mathbb {R}}^n\times ({\mathbb {R}}_{\ge 0})^r$ is an equilibrium of (5) if and only if it satisfies (4).

Proof

The proof simply follows by noticing that $x^+=x$ if and only if $\nabla L(x,\lambda )=0$, which is (4a), and $\lambda ^+=\lambda$ if and only if $0=\max \{-\lambda ,\gamma g(x)\}$, which is equivalent to (4b) since $\lambda \ge 0$. $\square$

The discussion of Sect. 2.1 and Lemma 2 ultimately imply that (5) has a unique equilibrium $(x^\star ,\lambda ^\star )\in {\mathbb {R}}^n\times ({\mathbb {R}}_{\ge 0})^r$ satisfying (4) and such that $x^\star$ solves (2). In the remainder of the article, we study the stability and exponential attractiveness properties of such an equilibrium.

3 Main result

In this section, we state and discuss the main result of the article establishing semiglobal exponential stability of the optimal equilibrium $(x^\star ,\lambda ^\star )$ for Algorithm (5).

Theorem 1

Suppose that Assumptions 1 and 2 hold. Then, for every compact subset $\Xi _0\subseteq {\mathbb {R}}^n\times ({\mathbb {R}}_{\ge 0})^r$ of initial conditions for (5), there exists ${{\bar{\gamma }}}>0$, and for every $\gamma \in (0,{{\bar{\gamma }}})$, there exist $\mu =\mu (\gamma )\in (0,1)$ and $\sigma =\sigma (\gamma )>0$, such that every solution $(x,\lambda )$ of (5) with $(x^0,\lambda ^0)\in \Xi _0$ satisfies

$$\begin{aligned} \forall t\in {\mathbb {N}},\qquad |(x^t-x^\star ,\lambda ^t-\lambda ^\star )| \le \sigma \mu ^t |(x^0-x^\star ,\lambda ^0-\lambda ^\star )|. \end{aligned}$$

(6)

The proof of Theorem 1 is presented in Sect. 4. Clearly, (6) implies that the optimal equilibrium $(x^\star ,\lambda ^\star )$ is Lyapunov stable for (5) and semiglobally exponentially attractive with the convergence rate $\mu$ and the constant $\sigma$ depending on $\gamma$. As shown in the proof of the theorem (see, in particular, Sect. 4.7) for a fixed $\gamma >0$, the constants $\mu$ and $\sigma$ are estimated as

$$\begin{aligned} \mu&{:}{=}\sqrt{1 - \frac{1}{6}\min \left\{ 2,\,\gamma c_0,\,\gamma ^2 k_2^2\right\} } ,&\sigma&{:}{=}\sqrt{3}{\mu ^{-T}}, \end{aligned}$$

in which

$$\begin{aligned} T {:}{=}\frac{6(3K_0^2 - \min \{\gamma ^2h^2,\varepsilon ^2\} )}{\min \left\{ 2,\,\gamma c_0,\, \gamma ^2 k_2^2\right\} \min \left\{ \gamma ^2h^2,\varepsilon ^2\right\} }, \end{aligned}$$

for suitable positive constants $c_0,K_0,h,k_2,\varepsilon$ defined in the proof of Theorem 1 (see Sects. 4.1 and 4.2). In particular, $c_0$ is the convexity parameter of f such that (8) holds, $K_0>0$ is any scalar such that $\Xi _0\subseteq {\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star )$ (see (7)), $h{:}{=}\min _{i\notin A(x^\star )} |g_i(x^\star )|$, $k_2 >0$ is the Lipschitz constant of $(x,\lambda )\mapsto \nabla L(x,\lambda )$ on a suitably-defined compact superset of ${\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star )$ (see (9)), and $\varepsilon >0$ is a possibly “small” scalar fixed in (18) so that, for all $x\in {\mathbb {R}}^n$ satisfying $|x-x^\star |\le \varepsilon$, $g_i(x)<0$ for all $i\notin A(x^\star )$, and $\nabla g_\text {A}(x)^\top \nabla g_\text {A}(x)$ is uniformly positive definite.

The above estimates of $\mu$ and $\sigma$ highlight the worst-case dependency of the convergence properties of the algorithm from the stepsize ($\gamma$), the convexity properties of the cost function ($c_0$), the “size” of the domain of attraction ($K_0$), the smoothness of the cost function and the constraint functions ($k_2$), and the “regularity” (or independence) of the active constraints ($\varepsilon$). In this respect, we observe that (6) only gives a worst-case estimate of the error decrease, and it does not characterize exactly the actual algorithm’s convergence rate.

4 Proof of Theorem 1

In this section, we prove Theorem 1. We organize the proof in seven subsections. In Sects. 4.1 and 4.2, we first present some preliminary definitions and technical lemmas. In Sect. 4.3, we construct a Lyapunov candidate function that, unlike the one used by Uzawa in [29], includes a cross-term proportional to $\langle x-x^\star \,|\, \nabla g(x) (\lambda -\lambda ^\star ) \rangle$. In Sects. 4.4 and 4.5, we study the descent properties of such a Lyapunov candidate. The analysis is divided into two cases, depending on how x is far from $x^\star$. It turns out that the aforementioned cross-term is key to prove that the Lyapunov function decreases when x is close to $x^\star$, as it produces a negative term proportional to $|\tilde{\lambda }_\text {A}|^2$ in the evolution equation of the Lyapunov candidate (see (46)). In turn, this term was missing from Uzawa’s analysis in [29]. In Sect. 4.6, we use the Lyapunov candidate to establish equiboundedness of the solutions and convergence to the optimum $(x^\star ,\lambda ^\star )$. Finally, in Sect. 4.7, we prove the exponential bound (6).

We fix now, once and for all, an arbitrary compact set $\Xi _0\subseteq {\mathbb {R}}^n\times ({\mathbb {R}}_{\ge 0})^r$ for the initial conditions of (5). We stress that $\Xi _0$ can be any, arbitrarily large, compact set.

4.1 Preliminary definitions

Consider a $K_0 >0$ be such that

$$\begin{aligned} \Xi _0 \subseteq {\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star ). \end{aligned}$$

(7)

Let us fix once and for all

$$\begin{aligned} K \ge 2K_0 +1, \end{aligned}$$

and define

$$\begin{aligned} {\mathscr {K}}&{:}{=}{\overline{{\mathbb {B}}}}_{K}(x^\star ,\lambda ^\star ),&{\mathscr {K}}_x&{:}{=}\big \{ x\in {\mathbb {R}}^n \,:\,\exists \lambda \in {\mathbb {R}}^r, \ (x,\lambda )\in {\mathscr {K}}\big \}. \end{aligned}$$

Since f is strongly convex (Assumption 1-A), there exists $c_0>0$ such that

$$\begin{aligned} \forall x\in {\mathbb {R}},\quad \langle x-x^\star \,|\, \nabla f(x)-\nabla f(x^\star ) \rangle \ge c_0 |x-x^\star |^2. \end{aligned}$$

(8)

Since ${\mathscr {K}}$ is compact, the smoothness assumptions 1-A and 1-B together with the optimality conditions (4) imply the existence of $k_1,k_2,k_3,k_4>0$ such that

$$\begin{aligned} \begin{aligned} \forall&x,\xi \in {\mathscr {K}}_x,{} & {} |g(x) - g(\xi )|\le k_1 |x-\xi |, \\ \forall&(x,\lambda )\in {\mathscr {K}},{} & {} |\nabla L (x,\lambda )| \le k_2 (|x-x^\star | + |\lambda -\lambda ^\star |), \\ \forall&x,\xi \in {\mathscr {K}}_x,{} & {} |\nabla f(x) - \nabla f(\xi )| \le k_3 |x - \xi |, \\ \forall&x,\xi \in {\mathscr {K}}_x,{} & {} |\nabla g(x) - \nabla g(\xi )| \le k_4 |x - \xi |. \end{aligned} \end{aligned}$$

(9)

Moreover, we can define the following constants

$$\begin{aligned} \begin{aligned} k_5&{:}{=}\sup _{(x,\lambda ) \in {\mathscr {K}}} | \nabla L (x,\lambda )|,&k_6&{:}{=}\sup _{x \in {\mathscr {K}}_x} | \nabla g (x)|,&k_7&{:}{=}\sup _{x \in {\mathscr {K}}_x} |g(x)|. \end{aligned} \end{aligned}$$

(10)

Let $r_a\le r$ denote the number of active constraints at $x^\star$. Without loss of generality, we assume that these active constraints are associated with the indices $i\in \text {A}{:}{=}\{1,\dots , r_a\}$. Thus, we have $g_i(x^\star )=0$ for all $i\in \text {A}$, and $g_i(x^\star )<0$ for all $i\in \text {I}{:}{=}\{r_a+1,\dots ,r\}$. Let $\lambda _\text {A}{:}{=}(\lambda _{1},\dots ,\lambda _{r_a})$ collect all multipliers associated with active constraints, and $\lambda _{\text {I}}{:}{=}(\lambda _{r_a+1},\dots ,\lambda _r)$ those associated with inactive constraints. Let $g_\text {A}$ and $g_{\text {I}}$ be defined accordingly. Then

$$\begin{aligned} g_\text {A}(x^\star )&=0,&\lambda _\text {A}^\star&\ge 0,&g_{\text {I}}(x^\star )&<0,&\lambda _{\text {I}}^\star&=0. \end{aligned}$$

(11)

and, for all $(x,\lambda )\in {\mathbb {R}}^n\times ({\mathbb {R}}_{\ge 0})^r$,

$$\begin{aligned} |\lambda |^2&= |\lambda _\text {A}|^2 + |\lambda _\text {I}|^2,&\nabla g(x) \lambda = \nabla g_\text {A}(x) \lambda _\text {A}+\nabla g_\text {I}(x) \lambda _\text {I}. \end{aligned}$$

(12)

Moreover, Assumption 2 implies

$$\begin{aligned} \nabla g_\text {A}(x^\star )^\top \nabla g_\text {A}(x^\star )>0. \end{aligned}$$

(13)

Since $\nabla g$ is continuous (Assumption 1-B), there exist $q>0$ and ${{\bar{\varepsilon }}}_1>0$ such that the following conditions hold

$$\begin{aligned}&\forall x\in {\mathbb {R}}^n,\quad |x-x^\star |\le {{\bar{\varepsilon }}}_1 \ \implies \ \nabla g_\text {A}(x)^\top \nabla g_\text {A}(x) \ge q I, \end{aligned}$$

(14a)

$$\begin{aligned}&\forall x\in {\mathbb {R}}^n,\quad |x-x^\star |\le {{\bar{\varepsilon }}}_1 \ \implies \ g_\text {I}(x) <0. \end{aligned}$$

(14b)

For ease of notation, define

$$\begin{aligned} \begin{aligned} \alpha _1 \,&{:}{=}\, \frac{q}{ k_4 k_5+k_6 (k_3+k_4 |\lambda ^\star |)}, \qquad \alpha _2 \, {:}{=}\, \frac{k_4 k_5 + k_6 (k_3+k_4 |\lambda ^\star |)}{2\alpha _1} + k_1k_6, \\ \alpha _3\,&{:}{=}\, \frac{3k_1k_2k_6+k_2k_4k_5 }{2}, \qquad \alpha _4 \,{:}{=}\, \frac{k_1k_2k_6+3k_2k_4k_5}{2}, \\ \alpha _7 \,&{:}{=}\, k_2k_6+ + \frac{\beta }{2}\big (K k_4k_6+ k_4k_5 + k_2k_6 \big ), \qquad \alpha _8 \, {:}{=}\, \frac{\beta }{2} \left( k_1^2k_6^2 + Kk_4k_6k_2^2\right) , \\ \alpha _9\,&{:}{=}\, \beta \left( \frac{k_2k_6}{2}+ k_6^2\right) + k_2k_6, \qquad \alpha _{10} \, {:}{=}\, \beta \frac{K k_4k_6k_2^2}{2}, \\ \alpha _{11}\,&\, {:}{=}\frac{\beta }{2}\left( k_4k_5+k_2k_6 \frac{1+\delta _1+\delta _1^2}{\delta _1} \right) + k_2k_6 \frac{1+\delta _1}{\delta _1} + k_6^2 + \beta k_6^2 \frac{1+2\delta _1}{4\delta _1} + \beta K k_4k_6, \end{aligned} \end{aligned}$$

(15)

in which we denote

$$\begin{aligned} \beta \,&{:}{=}\, 6 \frac{k_2^2}{q},&\delta _1 \,&{:}{=}\, \frac{k_2^2}{8\alpha _9},&\delta _2&{:}{=}{\left\{ \begin{array}{ll} 0 &{} \text {if}\ r=r_a\\ \frac{c_0}{2(r-r_a)(1+\beta ) k_1}&{} \text {if}\ r<r_a. \end{array}\right. } \end{aligned}$$

(16)

Next, define

$$\begin{aligned} h \,&{:}{=}\, \min _{i\in \text {I}}|g_i(x^\star )| ,&{{\bar{\varepsilon }}}\,&{:}{=}\, \min \left\{ {{\bar{\varepsilon }}}_1,\ \frac{h}{4k_1(1+2\beta )}\right\} , \end{aligned}$$

(17)

(notice that $h>0$ in view of (11)) and we fix once and for all (and arbitrarily)

$$\begin{aligned} \varepsilon \in (0,{{\bar{\varepsilon }}}). \end{aligned}$$

(18)

Finally, with

$$\begin{aligned} {{\bar{\gamma }}}_1\,&{:}{=}\, \dfrac{1}{16 K_0 k_5}, \qquad {{\bar{\gamma }}}_2\,{:}{=}\, \dfrac{1}{2 k_5} ,\qquad {{\bar{\gamma }}}_3{:}{=}\dfrac{1}{16 K_0 k_7},\qquad {{\bar{\gamma }}}_4 \,{:}{=}\, \dfrac{1}{2k_7}, \end{aligned}$$

(19a)

$$\begin{aligned} {{\bar{\gamma }}}_5&\,{:}{=}\, \dfrac{1}{\beta k_6}, \qquad {{\bar{\gamma }}}_6 \,{:}{=}\, \dfrac{c_0 \varepsilon ^2}{\beta \big ( 4K_0^2 k_4 k_5 + 2K_0 k_6 k_7 + k_5 k_6K) + k_7^2 + k_5^2 } , \end{aligned}$$

(19b)

$$\begin{aligned} {{\bar{\gamma }}}_7\,&{:}{=}\, \min \left\{ \dfrac{c_0}{2(k_1^2+2k_2^2+\beta \alpha _2)},\ \sqrt{\dfrac{c_0}{2\beta \alpha _3}}\right\} ,\qquad {{\bar{\gamma }}}_8\, {:}{=}\, \dfrac{k_2^2}{2\beta \alpha _4} , \end{aligned}$$

(19c)

$$\begin{aligned} {{\bar{\gamma }}}_9 \,&{:}{=}\, \min \left\{ \frac{1}{2\sqrt{\alpha _{11}}},\ \frac{\delta _2}{4(1+\beta )k_1} \right\} ,\quad {{\bar{\gamma }}}_{10}\, {:}{=}\, \frac{h}{4 \alpha _{11} K} , \end{aligned}$$

(19d)

$$\begin{aligned} {{\bar{\gamma }}}_{11}\,&{:}{=}\, \min \left\{ \frac{c_0}{8\alpha _7} ,\, \frac{1}{2}\root 3 \of {\frac{c_0}{\alpha _{10}}} ,\,\frac{k_2}{2\sqrt{2\alpha _{10}}}\right\} , \quad {{\bar{\gamma }}}_{12}\, {:}{=}\, \frac{2h}{K k_2^2}, \end{aligned}$$

(19e)

we fix arbitrarily, once and for all, the value of $\gamma$ as

$$\begin{aligned} \gamma \in (0,{{\bar{\gamma }}}),\qquad {{\bar{\gamma }}} {:}{=}\min _{i=1,\dots ,12} {{\bar{\gamma }}}_{i}. \end{aligned}$$

(20)

The specific value of each of the above-defined constants is motivated by the derivations carried out in the following subsections. We stated all the definitions here to highlight that no circular dependencies arise. Specifically, one can readily verify that: (i) the constants $K_0$ and K only depend on the optimal point $(x^\star ,\lambda ^\star )$ and the initialization set $\Xi _0$; (ii) the constants $k_1,\dots , k_7$, defined in (9)–(10), only depend on the functions f and g, on $(x^\star ,\lambda ^\star )$, and on the previously-defined constant K; (iii) q and ${\bar{\varepsilon }}_1$ in (14) only depend on g; (iv) $\beta$ only depends on $k_2$ and q; (v) $\delta _1$ and $\delta _2$ only depend on $\beta$ and $k_1,k_2,k_6$; (vi) the constants $\alpha _1,\dots ,\alpha _{11}$ only depend on the previously-defined quantities; (vii) h, ${{\bar{\varepsilon }}}$ and, hence, $\varepsilon$, only depend on g, $x^\star$, ${{\bar{\varepsilon }}}_1$, $k_1$ and $\beta$; (viii) the remaining constants ${{\bar{\gamma }}}_1,\dots ,{{\bar{\gamma }}}_{12}$ only depend on the previously-defined constants.

4.2 Preparatory lemmas

In this subsection, we prove some preliminary technical lemmas that will be used in the forthcoming analysis. For notational convenience, we let

$$\begin{aligned} \tilde{x}&= x-x^\star ,&\tilde{\lambda }&= \lambda -\lambda ^\star . \end{aligned}$$

In view of (5), these variables satisfy the recursion

$$\begin{aligned} \tilde{x}^+&= \tilde{x}- \gamma \nabla L(x,\lambda ), \end{aligned}$$

(21a)

$$\begin{aligned} \tilde{\lambda }^+&= \max \big \{ -\lambda ^\star ,\ \tilde{\lambda }+ \gamma g(x)\big \}. \end{aligned}$$

(21b)

Since $\lambda ^+ = \max \{0,\lambda +\gamma g(x)\} \ge \lambda + \gamma g(x)$ and since $\lambda ^\star \ge 0$ in view of (4), we have $-2 \langle \lambda ^+ \,|\, \lambda ^\star \rangle \le -2\langle \lambda \,|\, \lambda ^\star \rangle -2\gamma \langle \lambda ^\star \,|\, g(x) \rangle$. Therefore, we can write

$$\begin{aligned} \begin{aligned} |\tilde{x}^+|^2&= |\tilde{x}-\gamma \nabla L(x,\lambda )|^2 = |\tilde{x}|^2 -2\gamma \langle \tilde{x} \,|\, \nabla L(x,\lambda ) \rangle +\gamma ^2|\nabla L(x,\lambda )|^2 \end{aligned} \end{aligned}$$

(22a)

and

$$\begin{aligned} \begin{aligned} |\tilde{\lambda }^+|^2&= \big | \lambda ^+ - \lambda ^\star \big |^2 = |\lambda ^+|^2 - 2\langle \lambda ^+ \,|\, \lambda ^\star \rangle +|\lambda ^\star |^2 \\&\le |\lambda +\gamma g(x)|^2 - 2\langle \lambda \,|\, \lambda ^\star \rangle -2\gamma \langle \lambda ^\star \,|\, g(x) \rangle +|\lambda ^\star |^2 \\&\le |\lambda |^2 +|\lambda ^\star |^2 -2\langle \lambda \,|\, \lambda ^\star \rangle + 2\gamma \langle \tilde{\lambda } \,|\, g(x) \rangle + \gamma ^2 |g(x)|^2 \\&= |\tilde{\lambda }|^2 + 2\gamma \langle \tilde{\lambda } \,|\, g(x) \rangle + \gamma ^2 |g(x)|^2. \end{aligned} \end{aligned}$$

(22b)

Lemma 3

Suppose that Assumption 1 holds and let $c_0>0$ be given by (8). Then,

$$\begin{aligned} \forall (x,\lambda )\in {\mathbb {R}}^n\times ({\mathbb {R}}_{\ge 0})^r,\quad \langle \tilde{x} \,|\, \nabla f(x) + \nabla g (x) \lambda \rangle - \langle \tilde{\lambda } \,|\, g(x) \rangle \ge c_0 |\tilde{x}|^2 . \end{aligned}$$

Proof

Since $\lambda ^\star \ge 0$ and $\langle \tilde{x} \,|\, \nabla f(x) \rangle \ge \langle \tilde{x} \,|\, \nabla f(x^\star ) \rangle + c_0|\tilde{x}|^2$ (see the strong convexity condition in (8)), we can write

$$\begin{aligned}&\langle \tilde{x} \,|\, \nabla f(x)+ \nabla g(x) \lambda \rangle - \langle \tilde{\lambda } \,|\, g(x) \rangle \\&\quad = \langle \tilde{x} \,|\, \nabla f(x) \rangle + \langle \nabla g(x)^\top \tilde{x}- g(x) \,|\, \lambda \rangle + \langle g(x) \,|\, \lambda ^\star \rangle \\&\quad \ge \langle \tilde{x} \,|\, \nabla f(x^\star ) \rangle + c_0|\tilde{x}|^2 + \langle \nabla g(x)^\top \tilde{x}- g(x) \,|\, \lambda \rangle + \langle g(x^\star ) + \nabla g(x^\star )^\top \tilde{x} \,|\, \lambda ^\star \rangle \\&\quad = c_0|\tilde{x}|^2 + \langle \tilde{x} \,|\, \underbrace{ \nabla f(x^\star ) + \nabla g(x^\star ) \lambda ^\star }_{=0} \rangle + \underbrace{ \langle g(x^\star ) \,|\, \lambda ^\star \rangle }_{=0\text { by} \, 4} + \underbrace{\langle \nabla g(x)^\top \tilde{x}- g(x) \,|\, \lambda \rangle }_{\begin{array}{c} \ge -\langle g(x^\star ) \,|\, \lambda \rangle \ge 0\\ \text {by}\, 4\, \text {and} \, 23\, \text {with} (w,y)=(x^\star ,x) \end{array} } \\&\quad \ge c_0|\tilde{x}|^2, \end{aligned}$$

where, in the first inequality, we also used convexity⁴ of the $g_i$ (cf. condition (23) with the identification $(w,y)=(x,x^\star )$).$\square$

Lemma 4

Suppose that Assumption 1 holds, and let $\gamma$ satisfy (20). Then, system (5) satisfies

$$\begin{aligned}&(x,\lambda )\in {\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star ) \implies (x^+,\lambda ^+) \in {\mathscr {K}}. \end{aligned}$$

Proof

With reference to the constants introduced in (9)–(10), notice that, since $\gamma <\min \{{{\bar{\gamma }}}_1,{{\bar{\gamma }}}_2,{{\bar{\gamma }}}_3,{{\bar{\gamma }}}_4\}$ (see 20) and ${\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star )\subseteq {\mathscr {K}}$, then (19a), (21), and (22) imply

$$\begin{aligned} |\tilde{x}^+|^2&= |\tilde{x}|^2 -2\gamma \langle \tilde{x} \,|\, \nabla L(x,\lambda ) \rangle + \gamma ^2 |\nabla L(x,\lambda )|^2 \\&\le |\tilde{x}|^2 + \gamma 4 K_0 k_5 + \gamma ^2 k_5^2 \le |\tilde{x}|^2 + \frac{1}{2} \\ |\tilde{\lambda }^+|^2&\le |\tilde{\lambda }|^2 + 2\gamma \langle \tilde{\lambda } \,|\, g(x) \rangle + \gamma ^2 |g(x)|^2 \le |\tilde{\lambda }|^2 + \gamma 4K_0 k_7 + \gamma ^2 k_7^2 \le |\tilde{\lambda }|^2 + \frac{1}{2} \end{aligned}$$

for all $(x,\lambda )\in {\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star )$. In the previous inequalities, we have used the fact that $\gamma <\min \{{{\bar{\gamma }}}_1,{{\bar{\gamma }}}_2,{{\bar{\gamma }}}_3,{{\bar{\gamma }}}_4\}$ implies

$$\begin{aligned} \gamma 4K_0k_5 + \gamma ^2 k_5^2&< {{\bar{\gamma }}}_1 4K_0 k_5 + {{\bar{\gamma }}}_2^2k_5^2 = \frac{1}{4}+ \frac{1}{4} = \frac{1}{2} , \\ \gamma 4K_0 k_7 + \gamma ^2 k_7^2&< {{\bar{\gamma }}}_3 4 K_0 k_7 + {{\bar{\gamma }}}_4^2 k_7^2 =\frac{1}{4}+\frac{1}{4} = \frac{1}{2}. \end{aligned}$$

Combining the previous inequalities, we then get

$$\begin{aligned} |\tilde{x}^+|^2 + |\tilde{\lambda }^+|^2\le |\tilde{x}|^2+ |\tilde{\lambda }|^2+1&\implies |(\tilde{x}^+,\tilde{\lambda }^+)| \le |(\tilde{x},\tilde{\lambda })|+1 \le 2K_0 +1, \end{aligned}$$

which implies $(x^+,\lambda ^+)\in {\mathscr {K}}$. $\square$

Lemma 5

Every solution of (5) satisfies $\lambda ^t \ge 0$ and $|\tilde{\lambda }^{t+1}-\tilde{\lambda }^t|\le \gamma |g(x^t)|$ for all $t\in {\mathbb {N}}$.

Proof

The fact that $\lambda ^t\ge 0$ for all $t\ge 0$ is obvious. Regarding the second claim, pick $i\in \{1,\dots ,r\}$ and $t\in {\mathbb {N}}$ arbitrarily. From (21b), we obtain

$$\begin{aligned} \tilde{\lambda }_i^{t+1} = \max \left\{ 0,\lambda _i^t + \gamma g_i(x^t)\right\} - \lambda ^\star _i. \end{aligned}$$

(24)

First, assume that $\lambda _i^t + \gamma g_i(x^t) \ge 0$. Then (24) yields $\tilde{\lambda }_i^{t+1}-\tilde{\lambda }_i^t = \gamma g_i(x^t)$, hence $|\tilde{\lambda }_i^{t+1}-\tilde{\lambda }_i^t| = \gamma |g_i(x^t)|$. On the other hand, suppose that $\lambda _i^t + \gamma g_i(x^t) < 0$. Since $\lambda _i^t\ge 0$, then $g_i(x^t)<0$, and (24) implies

$$\begin{aligned} |\tilde{\lambda }_i^{t+1}-\tilde{\lambda }_i^t| = |-\lambda ^\star _i -\tilde{\lambda }_i^t| = |-\lambda _i^t| = \lambda _i^t \le -\gamma g_i(x^t) = \gamma |g_i(x^t)|. \end{aligned}$$

Hence, in both cases, $|\tilde{\lambda }_i^{t+1}-\tilde{\lambda }_i^t| \le \gamma |g_i(x^t)|$. As i was arbitrary, we obtain

$$\begin{aligned} |\tilde{\lambda }^{t+1}-\tilde{\lambda }^t|^2 = \sum _{i=1,\dots ,r} |\tilde{\lambda }^{t+1}_i-\tilde{\lambda }_i^t|^2 \le \gamma ^2 \sum _{i=1,\dots ,r} |g_i(x^t)|^2 = \gamma ^2 |g(x^t)|^2, \end{aligned}$$

which concludes the proof. $\square$

4.3 The Lyapunov candidate

Next, we propose the Lyapunov candidate used later to establish stability and convergence. In this part, we prove some of its basic properties. Specifically, with $\beta$ defined in (16), we define the Lyapunov candidate

$$\begin{aligned} V(x,\lambda ) {:}{=}|\tilde{x}|^2 + |\tilde{\lambda }|^2 + \gamma \beta \langle \tilde{x} \,|\, \nabla g(x) \tilde{\lambda } \rangle . \end{aligned}$$

(25)

The following lemma shows that V is positive definite with respect to $(x^\star ,\lambda ^\star )$.

Lemma 6

Suppose that Assumption 1 holds, and let $\gamma$ satisfy (20). Then,

$$\begin{aligned} \forall (x,\lambda )\in {\mathscr {K}}, \qquad \frac{1}{2} |(\tilde{x},\tilde{\lambda })|^2 \le V(x,\lambda ) \le \frac{3}{2} |(\tilde{x},\tilde{\lambda })|^2. \end{aligned}$$

(26)

Proof

As for the upper bound in (26), notice that $(x,\lambda ) \in {\mathscr {K}}$ and $\gamma <{{\bar{\gamma }}}_5$ (see (19b)) imply

$$\begin{aligned} V(x,\lambda )&\le |\tilde{x}|^2 + |\tilde{\lambda }|^2 + \gamma \beta k_6 |\tilde{x}| |\tilde{\lambda }| \le |\tilde{x}|^2 + |\tilde{\lambda }|^2 + \gamma \frac{\beta k_6}{2} ( |\tilde{x}|^2 + |\tilde{\lambda }|^2) \\ {}&\le \frac{3}{2} ( |\tilde{x}|^2 + |\tilde{\lambda }|^2), \end{aligned}$$

in which, in the second inequality, we used the Young’s inequality $|\tilde{x}| |\tilde{\lambda }|\le \frac{1}{2}(|\tilde{x}|^2+ |\tilde{\lambda }|^2)$. Similarly, we obtain

$$\begin{aligned} |\tilde{x}|^2 + |\tilde{\lambda }|^2&= V(x,\lambda ) - \gamma \beta \langle \tilde{x} \,|\, \nabla g(x) \tilde{\lambda } \rangle \le V(x,\lambda ) + \gamma \beta k_6 |\tilde{x}||\tilde{\lambda }| \\ {}&\le V(x,\lambda ) + \frac{1}{2} (|\tilde{x}|^2 + |\tilde{\lambda }|^2), \end{aligned}$$

which gives the lower bound in (26).$\square$

Next, we define

$$\begin{aligned} \Omega _\rho {:}{=}\left\{ (x, \lambda ) \,:\,V(x, \lambda ) \le \rho \right\} , \end{aligned}$$

(27)

with

$$\begin{aligned} \rho {:}{=}\dfrac{3}{2} K_0^2. \end{aligned}$$

(28)

Then, the following lemma shows that the level set $\Omega _\rho$ lies in between ${\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star )$ and ${\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star )$.

Lemma 7

Suppose that Assumption 1 holds, and let $\gamma$ satisfy (20). Then,

$$\begin{aligned} {\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star ) \subseteq \Omega _\rho \subseteq {\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star ). \end{aligned}$$

Proof

In view of Lemma 6, we have

$$\begin{aligned} (x,\lambda ) \in {\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star ) \implies V(x,\lambda ) \le \frac{3}{2} K_0^2 = \rho \implies (x,\lambda ) \in \Omega _\rho , \end{aligned}$$

which proves the first inclusion. As for the second inclusion, we have

$$\begin{aligned} (x,\lambda ) \in \Omega _\rho&\implies |(\tilde{x},\tilde{\lambda })|^2 \le 2 V(x,\lambda ) \le 2\rho = 3 K_0^2 \\&\implies |(\tilde{x},\tilde{\lambda })| \le \sqrt{3} K_0 \le 2 K_0, \end{aligned}$$

which implies $(x,\lambda ) \in {\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star )$. $\square$

In the next two subsections, we show that the Lyapunov candidate V in (25) is strictly decreasing on $\Omega _\rho$ along the solutions of (5). We subdivide the proof in two cases, corresponding to the partition of $\Omega _\rho$ in the following two sets

$$\begin{aligned} \Omega _\rho ^{>\varepsilon } {:}{=}\big \{ (x,\lambda )\in \Omega _\rho \,:\,|x-x^\star |>\varepsilon \big \},\qquad \Omega _\rho ^{\le \varepsilon } {:}{=}\big \{ (x,\lambda )\in \Omega _\rho \,:\,|x-x^\star |\le \varepsilon \big \}, \nonumber \\ \end{aligned}$$

(29)

where, we recall, $\varepsilon$ has been fixed to satisfy (18).

As a preliminary step, common to both cases, we combine the inequalities (22) to obtain

$$\begin{aligned} V(x,\lambda )^+\le & {} |\tilde{x}|^2 + |\tilde{\lambda }|^2 + \gamma ^2\Big ( |g(x)|^2 + |\nabla L(x,\lambda )|^2\Big ) \nonumber \\{} & {} -2 \gamma \Big ( \langle \tilde{x} \,|\, \nabla L(x,\lambda ) \rangle - \langle \tilde{\lambda } \,|\, g(x) \rangle \Big ) + \gamma \beta \langle \tilde{x}^+ \,|\, \nabla g(x^+ ) \tilde{\lambda }^+ \rangle . \end{aligned}$$

(30)

4.4 Descent on $\Omega _\rho ^{>\varepsilon }$

We first focus on the last term of (30). In view of (21), and by adding and subtracting proper cross terms, we obtain

$$\begin{aligned} \begin{aligned} \gamma \beta \langle \tilde{x}^+ \,|\, \nabla g(x^+ ) \tilde{\lambda }^+ \rangle&= \gamma \beta \langle \tilde{x} \,|\, \nabla g(x^+ ) \tilde{\lambda }^+ \rangle - \gamma ^2 \beta \langle \nabla L (x,\lambda ) \,|\, \nabla g(x^+ )\tilde{\lambda }^+ \rangle \\&= \gamma \beta \langle \tilde{x} \,|\, \nabla g(x^+ ) \tilde{\lambda } \rangle + \gamma \beta \langle \tilde{x} \,|\, \nabla g(x^+ ) (\tilde{\lambda }^+-\tilde{\lambda }) \rangle \\&\qquad - \gamma ^2 \beta \langle \nabla L (x,\lambda ) \,|\, \nabla g(x^+ )\tilde{\lambda }^+ \rangle \\&= \gamma \beta \langle \tilde{x} \,|\, \nabla g(x) \tilde{\lambda } \rangle + \gamma \beta \langle \tilde{x} \,|\, ( \nabla g(x^+ ) -\nabla g(x)) \tilde{\lambda } \rangle \\&\qquad + \gamma \beta \langle \tilde{x} \,|\, \nabla g(x^+ )(\tilde{\lambda }^+-\tilde{\lambda }) \rangle - \gamma ^2 \beta \langle \nabla L (x,\lambda ) \,|\, \nabla g(x^+ )\tilde{\lambda }^+ \rangle . \end{aligned} \nonumber \\ \end{aligned}$$

(31)

We recall that from Lemmas 4 and 7 it follows that

$$\begin{aligned} (x,\lambda )\in \Omega _\rho \implies (x,\lambda )\in {\overline{{\mathbb {B}}}}_{2K_0}(x^\star ,\lambda ^\star ) \implies (x^+,\lambda ^+)\in {\mathscr {K}}. \end{aligned}$$

(32)

Therefore, if $(x,\lambda )\in \Omega _\rho$, the bounds (9) and (10) apply to both $(x,\lambda )$ and $(x^+,\lambda ^+)$. In particular, we have

$$\begin{aligned} |\nabla g(x^+)-\nabla g(x)|\le \gamma k_4 |\nabla L(x,\lambda )|. \end{aligned}$$

(33)

Hence, as long as $(x,\lambda )\in \Omega _\rho$, we can further manipulate (31) by using (33), (9), (10) and Lemma 5 to obtain

$$\begin{aligned} \gamma \beta \langle \tilde{x}^+ \,|\, \nabla g(x^+ )\tilde{\lambda }^+ \rangle&\le \gamma \beta \langle \tilde{x} \,|\, \nabla g(x) \tilde{\lambda } \rangle + \gamma ^2 \beta k_4 |\nabla L(x,\lambda )| |\tilde{x}|| \tilde{\lambda }| \\&\qquad + \gamma ^2 \beta k_6 |\tilde{x}| |g(x)| + \gamma ^2 \beta k_5k_6 |\tilde{\lambda }^+| \\&\le \gamma \beta \langle \tilde{x} \,|\, \nabla g(x) \tilde{\lambda } \rangle + \gamma ^2 \beta \big ( 4K_0^2 k_4 k_5 + 2K_0 k_6 k_7 + k_5 k_6 K \big ) , \end{aligned}$$

in which we also used the fact that, since $(x,\lambda )\in \Omega _\rho$, then $|\tilde{\lambda }^+|\le K$ as implied by Lemma 4. Hence, by using Lemma 3 and $\gamma <{{\bar{\gamma }}}_6$ (see (19b)), from (30) we obtain

$$\begin{aligned}&V(x,\lambda )^+ - V(x,\lambda ) \\&\quad \le - 2 \gamma c_0 |\tilde{x}|^2 + \gamma ^2\Big ( g(x)^2 + |\nabla L(x,\lambda )|^2 \Big ) \\&\qquad + \gamma ^2 \beta \big ( 4K_0^2 k_4 k_5 + 2K_0 k_6 k_7 + k_5 k_6K \big ) \\&\quad \le - 2 \gamma c_0 |\tilde{x}|^2 + \gamma ^2\Big ( \beta \big ( 4K_0^2 k_4 k_5 + 2K_0 k_6 k_7 + k_5 k_6K\big ) + k_7^2 + k_5^2 \Big ) \\&\quad \le - 2 \gamma c_0 |\tilde{x}|^2 + \gamma c_0 \varepsilon ^2. \end{aligned}$$

Since $(x,\lambda ) \in \Omega _\rho ^{>\varepsilon } \implies |\tilde{x}|^2 \ge \varepsilon ^2$, we finally conclude that

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{>\varepsilon },\qquad V(x,\lambda )^+- V(x,\lambda ) \le - \gamma c_0 \varepsilon ^2 < 0. \end{aligned}$$

(34)

4.5 Descent on $\Omega _\rho ^{\le \varepsilon }$

Recall the decomposition of $\lambda$ in $\lambda _\text {A}$ and $\lambda _\text {I}$ (Sect. 4.1), in which $\text {A}=\{1,\dots , r_a\}$ is the set of indices i associated with active constraints (i.e., satisfying $g_i(x^\star )=0$) and $\text {I}=\{r_a+1,\dots ,r\}$ that of indices i associated with inactive constraints (i.e., satisfying $g_i(x^\star )<0$). Notice that (11) implies $\tilde{\lambda }_\text {I}=\lambda _\text {I}$. Moreover, since $\nabla g(x)\tilde{\lambda }=\nabla g_\text {A}(x)\tilde{\lambda }_\text {A}+ \nabla g_\text {I}(x)\tilde{\lambda }_\text {I}= \nabla g_\text {A}(x)\tilde{\lambda }_\text {A}+ \nabla g_\text {I}(x)\lambda _\text {I}$, we can rewrite V as

$$\begin{aligned} V(x,\lambda ) = V_\text {A}(x,\lambda ) +V_\text {I}(x,\lambda ), \end{aligned}$$

(35)

in which

$$\begin{aligned} V_\text {A}(x,\lambda )&{:}{=}|\tilde{x}|^2 + |\tilde{\lambda }_\text {A}|^2 + \gamma \beta \langle \tilde{x} \,|\, \nabla g_\text {A}(x)\tilde{\lambda }_\text {A} \rangle , \end{aligned}$$

(36a)

$$\begin{aligned} V_\text {I}(x,\lambda )&{:}{=}|\lambda _\text {I}|^2 + \gamma \beta \langle \tilde{x} \,|\, \nabla g_\text {I}(x)\lambda _\text {I} \rangle . \end{aligned}$$

(36b)

Notice that $V_\text {A}(x,\lambda )$ only depends on $\lambda _\text {A}$, and not on $\lambda _\text {I}$. In the next sections we analyze the behavior of $V_\text {A}$ and $V_\text {I}$ on $\Omega _\rho ^{\le \varepsilon }$.

4.5.1 Bounding $V_\text {A}(x,\lambda )^+$ on $\Omega _\rho ^{\le \varepsilon }$

With slight abuse of notation, define

$$\begin{aligned} \nabla L_\text {A}(x,\lambda _\text {A})&{:}{=}\nabla f(x)+\nabla g_\text {A}(x)\lambda _\text {A},&x^+_\text {A}&{:}{=}x - \gamma \nabla L_\text {A}(x,\lambda _\text {A}),&\tilde{x}^+_\text {A}&{:}{=}x^+_\text {A}- x^\star . \end{aligned}$$

(37)

We notice that, in view of (37), if $\lambda _{\text {I}}=0$, then $x^+=x_\text {A}^+$.

With the previous definitions in mind, notice that (12) implies

$$\begin{aligned} \nabla L(x,\lambda )&= \nabla L_\text {A}(x,\lambda _\text {A})+\nabla g_\text {I}(x)\lambda _\text {I}, \\ \tilde{x}_\text {A}^+&= \tilde{x}- \gamma \nabla L_\text {A}(x,\lambda _\text {A}) = \tilde{x}^+ + \gamma \nabla g_\text {I}(x)\tilde{\lambda }_\text {I}. \end{aligned}$$

In addition, bounds analogous to (9) and (22b) hold for $L_\text {A}$ and $\lambda _\text {A}$. Hence, using (12), (22a), and proceeding as in (22b), we obtain

$$\begin{aligned} \begin{aligned} V_\text {A}(x,\lambda )^+&\le U(x,\lambda ) +W(x,\lambda ), \end{aligned} \end{aligned}$$

(38)

in which

$$\begin{aligned} \begin{aligned} U(x,\lambda )&{:}{=}|\tilde{x}|^2 + |\tilde{\lambda }_\text {A}|^2 + \gamma ^2\Big ( |g_\text {A}(x)|^2+|\nabla L_\text {A}(x,\lambda _\text {A})|^2\Big ) \\&\quad - 2\gamma \Big ( \langle \tilde{x} \,|\, \nabla L_\text {A}(x,\lambda _\text {A}) \rangle - \langle \tilde{\lambda }_\text {A} \,|\, g_\text {A}(x) \rangle \Big ) \\&\quad +\gamma \beta \langle \tilde{x}^+_\text {A} \,|\, \nabla g_\text {A}(x^+_\text {A}) \tilde{\lambda }_\text {A}^+ \rangle \end{aligned}\nonumber \\ \end{aligned}$$

(39)

and

$$\begin{aligned} \begin{aligned} W(x,\lambda )&{:}{=}{\mathscr {E}}_1+{\mathscr {E}}_2+{\mathscr {E}}_3+{\mathscr {E}}_4,\\ {\mathscr {E}}_1&{:}{=}\gamma ^2 \left( 2\langle \nabla L_\text {A}(x,\lambda _\text {A}) \,|\, \nabla g_\text {I}(x)\lambda _\text {I} \rangle + |\nabla g_\text {I}(x)\lambda _\text {I}|^2 \right) ,\\ {\mathscr {E}}_2&{:}{=}- 2\gamma \langle \tilde{x} \,|\, \nabla g_\text {I}(x)\lambda _\text {I} \rangle , \\ {\mathscr {E}}_3&{:}{=}-\gamma ^2\beta \langle \nabla g_\text {I}(x)\lambda _\text {I} \,|\, \nabla g_\text {A}(x^+)\tilde{\lambda }_\text {A}^+ \rangle ,\\ {\mathscr {E}}_4&{:}{=}\gamma \beta \langle \tilde{x}^+_\text {A} \,|\, (\nabla g_\text {A}(x^+)-\nabla g_\text {A}(x^+_\text {A}))\tilde{\lambda }_\text {A}^+ \rangle . \end{aligned} \nonumber \\ \end{aligned}$$

(40)

We notice that $U(x,\lambda )$ only depends on $\lambda _\text {A}$, and not on $\lambda _\text {I}$.

In the following, we bound the two terms in (38) separately. As for $U(x,\lambda )$, we start by noticing that (4a), (8), (9), and (11) imply

$$\begin{aligned}&|g_\text {A}(x)| = |g_\text {A}(x)-g_\text {A}(x^\star )| \le k_1 |\tilde{x}| , \end{aligned}$$

(41a)

$$\begin{aligned}&\nabla L_\text {A}(x^\star ,\lambda _\text {A}^\star ) =\nabla L(x^\star ,\lambda ^\star ) = 0, \end{aligned}$$

(41b)

$$\begin{aligned}&|\nabla L_\text {A}(x,\lambda _\text {A})|=|\nabla L_\text {A}(x,\lambda _\text {A})-\nabla L_\text {A}(x^\star ,\lambda _\text {A}^\star )|\le k_2\big (|\tilde{x}|+|\tilde{\lambda }_\text {A}|\big ), \end{aligned}$$

(41c)

$$\begin{aligned}&\langle \tilde{x} \,|\, \nabla L_\text {A}(x,\lambda _\text {A}) \rangle - \langle \tilde{\lambda }_\text {A} \,|\, g_\text {A}(x) \rangle \ge c_0|\tilde{x}|^2, \end{aligned}$$

(41d)

for all $(x,\lambda ) \in \Omega _\rho$. In particular, (41d) can be derived by means of the same arguments used to prove Lemma 3 in view of (41b). Moreover, we observe that

$$\begin{aligned} (x,\lambda )\in \Omega _\rho \implies (x^+_\text {A}, (\lambda _\text {A},0)^+) \in {\mathscr {K}}\implies |\tilde{x}_\text {A}^+|^2+|\tilde{\lambda }_\text {A}^+|^2\le K^2. \end{aligned}$$

(42)

The implications (42) can be proved as follows. By Lemma 7, $(x,\lambda )\in \Omega _\rho \implies (x,\lambda )\in {\overline{{\mathbb {B}}}}_{2K_0}( x^\star ,\lambda ^\star )$. Thus, $|(\tilde{x},(\tilde{\lambda }_\text {A},0))|\le |(\tilde{x},(\tilde{\lambda }_\text {A},\lambda _\text {I}))|= |(\tilde{x},\tilde{\lambda })|\le 2K_0$ where, in the last equality, we have used $\lambda ^\star _\text {I}=0$. This implies $(x,(\lambda _\text {A},0))\in {\overline{{\mathbb {B}}}}_{2K_0}( x^\star ,\lambda ^\star )$. Moreover, by (37), $\lambda _\text {I}=0\implies x^+=x^+_\text {A}$. Therefore, from Lemma 4 we obtain $(x_\text {A}^+, (\lambda _\text {A},0)^+)=(x^+, (\lambda _\text {A},0)^+)\in {\mathscr {K}}$, which proves (42).

Conditions (9), (37) and (42) also imply

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ,\quad |\nabla g_\text {A}(x_\text {A}^+)-\nabla g_\text {A}(x)| \le k_4|x_\text {A}^+-x| =\gamma k_4 |\nabla L_\text {A}(x,\lambda _\text {A})|, \end{aligned}$$

(43)

which will be useful later in the forthcoming computations.

Next, by using (9), (41), and Lemma 3, we obtain

$$\begin{aligned} \begin{aligned} U(x,\lambda ) - V_\text {A}(x,\lambda )&= \gamma ^2\Big ( |g_\text {A}(x)|^2+|\nabla L_\text {A}(x,\lambda _\text {A})|^2\Big ) \\&\qquad - 2\gamma \Big ( \langle \tilde{x} \,|\, \nabla L_\text {A}(x,\lambda _\text {A}) \rangle - \langle \tilde{\lambda }_\text {A} \,|\, g_\text {A}(x) \rangle \Big ) \\&\qquad +\gamma \beta \langle \tilde{x}^+_\text {A} \,|\, \nabla g_\text {A}(x^+_\text {A}) \tilde{\lambda }_\text {A}^+ \rangle - \gamma \beta \langle \tilde{x} \,|\, \nabla g_\text {A}(x) \tilde{\lambda }_\text {A} \rangle \\&\le \big ( \gamma ^2 k_1^2 + \gamma ^2 2k_2^2 - 2 \gamma c_0 \big ) |\tilde{x}|^2 + \gamma ^2 2k_2^2 |\tilde{\lambda }_\text {A}|^2 \\&\qquad + \gamma \beta \left( \langle \tilde{x}^+_\text {A} \,|\, \nabla g_\text {A}(x^+_\text {A}) \tilde{\lambda }_\text {A}^+ \rangle - \langle \tilde{x} \,|\, \nabla g_\text {A}(x) \tilde{\lambda }_\text {A} \rangle \right) . \end{aligned} \nonumber \\ \end{aligned}$$

(44)

The last term in (44) can be expressed as

$$\begin{aligned} \langle \tilde{x}_\text {A}^+ \,|\, \nabla g_\text {A}(x_\text {A}^+) \tilde{\lambda }_\text {A}^+ \rangle - \langle \tilde{x} \,|\, \nabla g_\text {A}(x) \tilde{\lambda }_\text {A} \rangle = {\mathscr {T}}_1+{\mathscr {T}}_2+{\mathscr {T}}_3+{\mathscr {T}}_4+{\mathscr {T}}_5, \end{aligned}$$

(45)

in which

$$\begin{aligned} {\mathscr {T}}_1&{:}{=}\langle \tilde{x} \,|\, (\nabla g_\text {A}(x_\text {A}^+ )-\nabla g_\text {A}(x)) \tilde{\lambda }_\text {A} \rangle ,\\ {\mathscr {T}}_2&{:}{=}\langle \tilde{x} \,|\, \nabla g_\text {A}(x_\text {A}^+ )(\tilde{\lambda }_\text {A}^+-\tilde{\lambda }_\text {A}) \rangle ,\\ {\mathscr {T}}_3&{:}{=}- \gamma \langle \nabla L_\text {A}(x,\lambda _\text {A}) \,|\, \nabla g_\text {A}(x_\text {A}^+ )(\tilde{\lambda }_\text {A}^+-\tilde{\lambda }_\text {A}) \rangle ,\\ {\mathscr {T}}_4&{:}{=}\gamma \langle \nabla L_\text {A}(x,\lambda _\text {A}) \,|\, (\nabla g_\text {A}(x) - \nabla g_\text {A}(x_\text {A}^+ ) )\tilde{\lambda }_\text {A} \rangle ,\\ {\mathscr {T}}_5&{:}{=}- \gamma \langle \nabla L_\text {A}(x,\lambda _\text {A}) \,|\, \nabla g_\text {A}(x) \tilde{\lambda }_\text {A} \rangle . \end{aligned}$$

We now proceed in bounding all terms ${\mathscr {T}}_j$, $j=1,\dots ,5$, one-by-one. With $\alpha _1$ defined in (15), by using (43) and the Young’s inequality we obtain

$$\begin{aligned} {\mathscr {T}}_1 \le \gamma k_4 | \nabla L_\text {A}(x,\lambda _\text {A})| |\tilde{x}||\tilde{\lambda }_\text {A}| \le \gamma k_4 k_5 |\tilde{x}||\tilde{\lambda }_\text {A}| \le \gamma k_4 k_5 \left( \frac{1}{2\alpha _1} |\tilde{x}|^2 + \frac{\alpha _1}{2} |\tilde{\lambda }_\text {A}|^2 \right) , \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho$. Conditions (41), (42) and Lemma 5 also imply

$$\begin{aligned} {\mathscr {T}}_2&\le |\nabla g_\text {A}(x_\text {A}^+ )| |\tilde{x}| |\tilde{\lambda }_\text {A}^+-\tilde{\lambda }_\text {A}| \le \gamma k_6 |\tilde{x}| |g_\text {A}(x)| \le \gamma k_1k_6 |\tilde{x}|^2, \\ {\mathscr {T}}_3&\le \gamma ^2 |\nabla g_\text {A}(x_\text {A}^+ )| |\nabla L_\text {A}(x,\lambda _\text {A})| |g_\text {A}(x)| \le \gamma ^2 k_6 k_2 k_1 (|\tilde{x}|^2 + |\tilde{x}| |\tilde{\lambda }_\text {A}| ) \\&\le \gamma ^2 k_1 k_2 k_6 \left( \frac{3}{2} |\tilde{x}|^2 + \frac{1}{2} |\tilde{\lambda }_\text {A}|^2 \right) , \\ {\mathscr {T}}_4&\le \gamma |\nabla L_\text {A}(x,\lambda _\text {A}) ||\nabla g_\text {A}(x) - \nabla g_\text {A}(x^+_\text {A}) | |\tilde{\lambda }_\text {A}| \\&\le \gamma ^2 k_4 |\nabla L_\text {A}(x,\lambda _\text {A}) |^2 |\tilde{\lambda }_\text {A}| \le \gamma ^2k_2 k_4 k_5 (|\tilde{x}| |\tilde{\lambda }_\text {A}| + |\tilde{\lambda }_\text {A}|^2) \\&\le \gamma ^2k_2 k_4 k_5 \left( \frac{1}{2} |\tilde{x}|^2 + \frac{3}{2} |\tilde{\lambda }_\text {A}|^2 \right) , \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho$.

Finally, by using (41b) and $\nabla g_\text {A}(x)^\top \nabla g_\text {A}(x)\ge q I$ for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$ (see (14) and (18)), we obtain

$$\begin{aligned} {\mathscr {T}}_5&= -\gamma \langle \nabla L_\text {A}(x,\lambda _\text {A})-\nabla L_\text {A}(x^\star ,\lambda _\text {A}^\star ) \,|\, \nabla g_\text {A}(x)\tilde{\lambda }_\text {A} \rangle \nonumber \\&= - \gamma \langle \nabla f(x) -\nabla f(x^\star ) \,|\, \nabla g_\text {A}(x)\tilde{\lambda }_\text {A} \rangle - \gamma |\nabla g_\text {A}(x)\tilde{\lambda }_\text {A}|^2 \nonumber \\ {}&\qquad - \gamma \langle (\nabla g_\text {A}(x) - \nabla g_\text {A}(x^\star ))\lambda _\text {A}^\star \,|\, \nabla g_\text {A}(x)\tilde{\lambda }_\text {A} \rangle \nonumber \\&\le \gamma k_6 (k_3+k_4 |\lambda _\text {A}^\star |) |\tilde{x}| |\tilde{\lambda }_\text {A}| - \gamma q |\tilde{\lambda }_\text {A}|^2 \nonumber \\&\le \gamma k_6 (k_3+k_4 |\lambda ^\star |) \left( \frac{1}{2\alpha _1} |\tilde{x}|^2 + \frac{\alpha _1}{2} |\tilde{\lambda }_\text {A}|^2 \right) - \gamma q |\tilde{\lambda }_\text {A}|^2, \end{aligned}$$

(46)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

In view of the previous bounds, and by using (15) and (16), we can further manipulate (45) to obtain

$$\begin{aligned}&\langle \tilde{x}_\text {A}^+ \,|\, \nabla g_\text {A}(x_\text {A}^+) \tilde{\lambda }_\text {A}^+ \rangle -\langle \tilde{x} \,|\, \nabla g_\text {A}(x) \tilde{\lambda }_\text {A} \rangle \\&\quad \le \gamma \bigg ( \frac{k_4 k_5 + k_6 (k_3+k_4 |\lambda ^\star |)}{2\alpha _1} + k_1k_6 + \gamma \frac{3k_1k_2k_6+k_2k_4k_5 }{2} \bigg ) |\tilde{x}|^2 \\&\quad \qquad + \gamma \bigg ( -q + \frac{ (k_4 k_5+k_6 (k_3+k_4 |\lambda ^\star |)) \alpha _1}{2} + \gamma \frac{k_1k_2k_6+3k_2k_4k_5}{2} \bigg ) |\tilde{\lambda }_\text {A}|^2 \\&\quad = \gamma \big ( \alpha _2 + \gamma \alpha _3\big ) |\tilde{x}|^2 + \gamma \left( -\frac{1}{2} q + \gamma \alpha _4\right) |\tilde{\lambda }_\text {A}|^2 \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

Then, going back to (44), we get

$$\begin{aligned} U(x,\lambda ) - V_\text {A}(x,\lambda )&\le \gamma \Big ( \gamma \big (k_1^2 + 2k_2^2+ \beta \alpha _2\big ) + \gamma ^2 \beta \alpha _3 - 2c_0\Big ) |\tilde{x}|^2\\&\qquad + \gamma ^2\left( 2k_2^2 + \gamma \beta \alpha _4 -\frac{1}{2} \beta q \right) |\tilde{\lambda }_\text {A}|^2 \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. By using the definition of $\beta$ given in (16) and $\gamma <{{\bar{\gamma }}}_7$ (see (19c)), we obtain

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad U(x,\lambda ) - V_\text {A}(x,\lambda ) \le -\gamma c_0 |\tilde{x}|^2 + \gamma ^2\big (\gamma \beta \alpha _4 -k_2^2\big )|\tilde{\lambda }_\text {A}|^2. \end{aligned}$$

By using $\gamma <{{\bar{\gamma }}}_8$ (see 19c), we can finally write

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad U(x,\lambda ) \le V_\text {A}(x,\lambda ) -\gamma c_0 |\tilde{x}|^2 -\frac{\gamma ^2k_2^2}{2}|\tilde{\lambda }_\text {A}|^2. \end{aligned}$$

Summarizing the bounds derived so far, from (38) we obtain

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad V_\text {A}(x,\lambda )^+ \le V_\text {A}(x,\lambda ) -\gamma c_0 |\tilde{x}|^2 -\frac{\gamma ^2k_2^2}{2}|\tilde{\lambda }_\text {A}|^2 + W(x,\lambda ), \nonumber \\ \end{aligned}$$

(47)

and we can now proceed in bounding $W(x,\lambda )$.

With reference to the definition of $W(x,\lambda )$ in (40), we bound the terms ${\mathscr {E}}_1,\dots ,{\mathscr {E}}_4$ one-by-one. Consider term ${\mathscr {E}}_1$. By using (9), (10), and (41c), we obtain

$$\begin{aligned} 2\langle \nabla L_\text {A}(x,\lambda _\text {A}) \,|\, \nabla g_\text {I}(x)\lambda _\text {I} \rangle&\le 2|\nabla L_\text {A}(x,\lambda _\text {A})| |\nabla g_\text {I}(x)| |\lambda _\text {I}| \\&\le k_2k_6 |\tilde{x}|^2 + k_2 k_6 \delta _1 |\tilde{\lambda }_\text {A}|^2 + k_2k_6 \dfrac{1+\delta _1}{\delta _1} |\lambda _\text {I}|^2 \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$, in which $\delta _1$ is defined in (16). As a consequence, we obtain

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad {\mathscr {E}}_1 \le \gamma ^2\left( k_2k_6 |\tilde{x}|^2 + k_2 k_6 \delta _1 |\tilde{\lambda }_\text {A}|^2 + k_2k_6 \dfrac{1+\delta _1}{\delta _1} |\lambda _\text {I}|^2 + k_6^2 |\lambda _\text {I}|^2\right) , \nonumber \\ \end{aligned}$$

(48)

Next, as for ${\mathscr {E}}_2$, we notice that $\lambda _{\text {I}}\ge 0$ and convexity of each $g_i$ (see (23)) imply

$$\begin{aligned} \begin{aligned} \langle \tilde{x} \,|\, \nabla g_\text {I}(x)\lambda _\text {I} \rangle&= \sum _{i=r_a+1}^r \langle \tilde{x} \,|\, \nabla g_i(x)\lambda _i \rangle = \sum _{i=r_a+1}^r \lambda _i \tilde{x}^\top \nabla g_i(x) \\&\ge \sum _{i=r_a+1}^r \lambda _i (g_i(x)-g_i(x^\star )) = \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I} \rangle . \end{aligned} \end{aligned}$$

(49)

Hence,

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\qquad {\mathscr {E}}_2 \le -2\gamma \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I} \rangle . \end{aligned}$$

(50)

Furthermore, regarding ${\mathscr {E}}_3$, by means of the same arguments of Lemma 5, one can show that $|\tilde{\lambda }_\text {A}^+-\tilde{\lambda }_\text {A}|\le \gamma |g_\text {A}(x)| \le \gamma k_1 |\tilde{x}|$ for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$ (in which we also used (41a). Thus, in view of Lemma 4,

$$\begin{aligned} \langle \nabla g_\text {I}(x)\lambda _\text {I} \,|\, \nabla g_\text {A}(x^+)\tilde{\lambda }_\text {A}^+ \rangle&\le |\nabla g_\text {I}(x)||\nabla g_\text {A}(x^+)| |\lambda _{\text {I}}|(|\tilde{\lambda }_{\text {A}}|+|\tilde{\lambda }_{\text {A}}^+-\tilde{\lambda }_\text {A}|) \\&\le k_6^2 |\lambda _\text {I}| \Big ( |\tilde{\lambda }_\text {A}| + \gamma k_1 |\tilde{x}| \Big ) \\&\le k_6^2 \delta _1 |\tilde{\lambda }_\text {A}|^2 + k_6^2 \frac{1+2\delta _1}{4\delta _1} |\lambda _\text {I}|^2 + \frac{\gamma ^2 k_1^2 k_6^2}{2}|\tilde{x}|^2, \end{aligned}$$

which implies

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad {\mathscr {E}}_3\le \beta \gamma ^2\left( k_6^2 \delta _1 |\tilde{\lambda }_\text {A}|^2 + k_6^2\frac{1+2\delta _1}{4\delta _1} |\lambda _\text {I}|^2 + \frac{\gamma ^2 k_1^2 k_6^2}{2}|\tilde{x}|^2\right) . \nonumber \\ \end{aligned}$$

(51)

Lastly, for what concerns ${\mathscr {E}}_4$, we use (42) to obtain $|\tilde{\lambda }_\text {A}^+| \le K$ and $|\nabla g_\text {A}(x^+)-\nabla g_\text {A}(x^+_\text {A}) |\le k_4|x^+-x_\text {A}^+|\le \gamma k_4 |\nabla g_\text {I}(x)\lambda _\text {I}|\le \gamma k_4k_6|\lambda _\text {I}|$ for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. These inequalities and (41c) imply

$$\begin{aligned} \langle \tilde{x}^+_\text {A} \,|\, (\nabla g_\text {A}(x^+)-\nabla g_\text {A}(x^+_\text {A}))\tilde{\lambda }_\text {A}^+ \rangle&\le | \tilde{x}^+_\text {A}| |\nabla g_\text {A}(x^+)-\nabla g_\text {A}(x^+_\text {A}) | |\tilde{\lambda }_\text {A}^+| \\&\le \gamma K k_4k_6 | \tilde{x}^+_\text {A}| | \lambda _\text {I}| \\&\le \gamma K k_4k_6 \left( | \tilde{x}| + \gamma |\nabla L_\text {A}(x,\lambda _\text {A})| \right) | \lambda _\text {I}| \\&\le \gamma K k_4k_6 ( (1+ \gamma k_2) |\tilde{x}| + \gamma k_2 |\tilde{\lambda }_\text {A}| ) | \lambda _\text {I}| \\&\le \gamma K k_4k_6 \left( \frac{(1+ \gamma k_2)^2}{2} |\tilde{x}|^2 + \frac{\gamma ^2 k_2^2}{2} |\tilde{\lambda }_\text {A}|^2 + | \lambda _\text {I}|^2\right) , \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. Hence, we obtain

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad {\mathscr {E}}_4\le \gamma ^2\beta K k_4k_6 \left( \frac{1+ \gamma ^2 k_2^2}{2}|\tilde{x}|^2 + \frac{\gamma ^2 k_2^2}{2} |\tilde{\lambda }_\text {A}|^2 + | \lambda _\text {I}|^2\right) . \nonumber \\ \end{aligned}$$

(52)

Using (40), (48), (50), (51), and (52), we obtain

$$\begin{aligned} \begin{aligned} W(x,\lambda )&\le -2\gamma \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I} \rangle \\&\quad + \gamma ^2\left( k_2 k_6 + \beta \gamma ^2 \dfrac{k_1^2k_6^2}{2} + \beta \frac{K k_4 k_6\left( 1+ \gamma ^2 k_2^2\right) }{2} \right) |\tilde{x}|^2 \\&\quad + \gamma ^2\bigg ( k_2 k_6 \dfrac{1+\delta _1}{\delta _1} + k_6^2 + \beta k_6^2 \dfrac{1+2\delta _1}{4\delta _1} + \beta K k_4 k_6 \bigg )|\lambda _\text {I}|^2 \\&\quad +\gamma ^2 \left( k_2k_6\delta _1 + \beta k_6^2\delta _1 + \gamma ^2\beta \frac{K k_4 k_6 k_2^2}{2} \right) |\tilde{\lambda }_\text {A}|^2 \end{aligned}\nonumber \\ \end{aligned}$$

(53)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

Finally, we can further bound (47) using (53) as

$$\begin{aligned} \begin{aligned} V_\text {A}(x,\lambda )^+&\le V_\text {A}(x,\lambda ) -2\gamma \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I} \rangle \\&\quad +\gamma \left( \gamma \left( k_2 k_6 + \beta \gamma ^2 \dfrac{k_1^2k_6^2}{2} + \beta \frac{K k_4 k_6\left( 1+ \gamma ^2 k_2^2\right) }{2} \right) - c_0\right) |\tilde{x}|^2\\&\quad + \gamma ^2\bigg ( k_2 k_6 \dfrac{1+\delta _1}{\delta _1} + k_6^2 + \beta k_6^2 \dfrac{1+2\delta _1}{4\delta _1} + \beta K k_4 k_6 \bigg )|\lambda _\text {I}|^2 \\&\quad +\gamma ^2 \left( k_2k_6\delta _1 + \beta k_6^2\delta _1 + \gamma ^2\beta \frac{K k_4 k_6 k_2^2}{2}-\frac{k_2^2}{2} \right) |\tilde{\lambda }_\text {A}|^2, \end{aligned}\nonumber \\ \end{aligned}$$

(54)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

4.5.2 Bounding $V_\text {I}(x,\lambda )^+$ on $\Omega _\rho ^{\le \varepsilon }$

Consider now the function $V_\text {I}$, defined in (36b). We start noticing that, since $\tilde{\lambda }_\text {I}=\lambda _\text {I}$, then (1b) implies

$$\begin{aligned} \forall i\in \text {I},\qquad |\tilde{\lambda }_i^+|^2- |\tilde{\lambda }_i|^2 = {\left\{ \begin{array}{ll} - |\lambda _i|^2 &{} \lambda _i +\gamma g_i(x)\le 0\\ \gamma \big ( 2\lambda _i + \gamma g_i(x) \big ) g_i(x) &{} \lambda _i+ \gamma g_i(x)>0. \end{array}\right. } \end{aligned}$$

In view of (14b) and (18), $g_i(x)<0$ holds for all $i\in \text {I}$ and all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. Thus, $\lambda _i + \gamma g_i(x)>0$ implies

$$\begin{aligned} \gamma \big ( 2\lambda _i + \gamma g_i(x) \big ) g_i(x) = \gamma g_i(x) \lambda _i + \gamma \big ( \lambda _i + \gamma g_i(x) \big ) g_i(x) < \gamma g_i(x) \lambda _i. \end{aligned}$$

Therefore, for every $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$, one has

$$\begin{aligned} |\tilde{\lambda }_\text {I}^+|^2 - |\tilde{\lambda }_\text {I}|^2 = \sum _{i=r_a+1}^{r} \Big (|\tilde{\lambda }_i^+|^2- |\tilde{\lambda }_i|^2 \Big ) \le \sum _{i=r_a+1}^{r} \max \{ -|\lambda _i|^2, \gamma g_i(x) \lambda _i \}. \nonumber \\ \end{aligned}$$

(55)

We now consider the increment of the cross term in $V_\text {I}$, which satisfies

$$\begin{aligned} \langle \tilde{x}^+ \,|\, \nabla g_\text {I}(x^+)\lambda _\text {I}^+ \rangle&- \langle \tilde{x} \,|\, \nabla g_\text {I}(x)\lambda _\text {I} \rangle = \langle \tilde{x} \,|\, (\nabla g_\text {I}(x^+)-\nabla g_\text {I}(x))\lambda _\text {I}^+ \rangle \\&\qquad \qquad -\gamma \langle \nabla L(x,\lambda ) \,|\, \nabla g_\text {I}(x^+)\lambda _\text {I}^+ \rangle +\langle \tilde{x} \,|\, \nabla g_\text {I}(x)(\lambda _\text {I}^+-\lambda _\text {I}) \rangle . \end{aligned}$$

We bound the three terms one by one. First, notice that (14b) and (55) imply $|\lambda _\text {I}^+|\le |\lambda _\text {I}|$ for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. Hence, proceeding as in previous section, we obtain

$$\begin{aligned} \langle \tilde{x} \,|\, (\nabla g_\text {I}(x^+)-\nabla g_\text {I}(x))\lambda _\text {I}^+ \rangle \le \gamma k_4 |\tilde{x}||\nabla L(x,\lambda )| |\lambda _\text {I}| \le \gamma \frac{k_4 k_5}{2} \left( |\tilde{x}|^2 + |\lambda _\text {I}|^2\right) \end{aligned}$$

and

$$\begin{aligned} -\gamma \langle \nabla L(x,\lambda ) \,|\, \nabla g_\text {I}(x^+)\lambda _\text {I}^+ \rangle&\le \gamma |\nabla L(x,\lambda )| |\nabla g_\text {I}(x^+)| |\lambda _\text {I}| \\&\le \gamma k_2 k_6 (|\tilde{x}|+|\tilde{\lambda }|) |\lambda _\text {I}| \\&\le \gamma \frac{k_2k_6}{2} \left( |\tilde{x}|^2 + \delta _1 |\tilde{\lambda }_\text {A}|^2 + \frac{1+\delta _1+\delta _1^2}{\delta _1} |\lambda _\text {I}|^2 \right) \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. Lastly, since (14b) implies $\lambda _i^+-\lambda _i\le 0$ for all $i\in \text {I}$ and all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$, then using convexity of each $g_i$ (see (23)) as in (49), we obtain

$$\begin{aligned} \langle \tilde{x} \,|\, \nabla g_\text {I}(x)(\lambda _\text {I}^+-\lambda _\text {I}) \rangle = \sum _{i=r_a+1}^r (\lambda _i^+-\lambda _i) \tilde{x}^\top \nabla g_i(x) \le \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I}^+-\lambda _\text {I} \rangle \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

Combining the previous bounds and (55), we can write

$$\begin{aligned} \begin{aligned} V_\text {I}(x,\lambda )^+ - V_\text {I}(x,\lambda )&= |\tilde{\lambda }_\text {I}^+|^2-|\tilde{\lambda }_\text {I}|^2 + \gamma \beta \langle \tilde{x}^+ \,|\, \nabla g_\text {I}(x^+)\tilde{\lambda }_\text {I}^+ \rangle - \gamma \beta \langle \tilde{x} \,|\, \nabla g_\text {I}(x)\tilde{\lambda }_\text {I} \rangle \\&\le \sum _{i=r_a+1}^{r} \max \{ - |\lambda _i|^2, \gamma g_i(x) \lambda _i \} + \gamma \beta \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I}^+-\lambda _\text {I} \rangle \\&\quad +\gamma ^2\frac{\beta }{2} \left( k_4 k_5 + k_2 k_6 \right) |\tilde{x}|^2 + \gamma ^2\beta \delta _1 \frac{k_2 k_6}{2} |\tilde{\lambda }_\text {A}|^2 \\&\quad + \gamma ^2\frac{\beta }{2}\left( k_4 k_5 + k_2 k_6 \frac{1+\delta _1+\delta _1^2}{\delta _1} \right) |\lambda _\text {I}|^2, \end{aligned} \nonumber \\ \end{aligned}$$

(56)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

4.5.3 Bounding $V(x,\lambda )^+$ on $\Omega _\rho ^{\le \varepsilon }$

Finally, we can merge the bounds (54) and (56) derived in previous Sects. 4.5.1 and 4.5.2 to obtain from (35) the following bound for V

$$\begin{aligned} \begin{aligned} V(x,\lambda )^+&\le V(x,\lambda ) + \sum _{i=r_a+1}^{r} \max \{ -|\lambda _i|^2, \gamma g_i(x) \lambda _i \} \\&\quad -2\gamma \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I} \rangle + \gamma \beta \langle g_\text {I}(x)-g_\text {I}(x^\star ) \,|\, \lambda _\text {I}^+-\lambda _\text {I} \rangle \\&\quad + \Big ( \gamma ^2 \alpha _7+ \gamma ^4 \alpha _8 -\gamma c_0\Big )|\tilde{x}|^2 + \gamma ^2\alpha _{11} |\lambda _\text {I}|^2 \\&\quad + \left( \gamma ^2 \left( \delta _1\alpha _9 - \frac{k_2^2}{2} \right) + \gamma ^4 \alpha _{10}\right) |\tilde{\lambda }_\text {A}|^2, \end{aligned} \nonumber \\ \end{aligned}$$

(57)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$, in which $\alpha _7,\alpha _8,\alpha _9,\alpha _{10},\alpha _{11}$ are defined in (15).

Grouping all terms involving $\lambda _i$ for $i\in \text {I}$ (recall that $\text {I}= \{r_a+1,\ldots ,r\}$), we can rewrite (57) as

$$\begin{aligned} \begin{aligned} V(x^+,\lambda ^+)&\le V(x,\lambda ) + \sum _{i=r_a+1}^{r} \Delta _i \ \ + \ \Big ( \gamma ^2 \alpha _7+ \gamma ^4 \alpha _8 -\gamma c_0\Big )|\tilde{x}|^2 \\&\quad + \left( \gamma ^2 \left( \delta _1\alpha _9 - \frac{k_2^2}{2} \right) + \gamma ^4 \alpha _{10}\right) |\tilde{\lambda }_\text {A}|^2, \end{aligned} \nonumber \\ \end{aligned}$$

(58)

in which

$$\begin{aligned} \Delta _i&{:}{=}\max \{ -|\lambda _i|^2, \gamma g_i(x) \lambda _i \} + \gamma ^2 \alpha _{11} |\lambda _i|^2 \\&\qquad -2\gamma (g_i(x)-g_i(x^\star ))\lambda _i + \gamma \beta (g_i(x)-g_i(x^\star )) (\lambda _i^+-\lambda _i) . \end{aligned}$$

Next, we derive a bound for $\Delta _i$. For each $i\in \text {I}$, we two cases may occur:

• C1 . $-|\lambda _i|^2 \ge \gamma g_i(x)\lambda _i$, which is true if and only if $|\lambda _i| \le \gamma |g_i(x)|$;

• C2 . $-|\lambda _i|^2 < \gamma g_i(x)\lambda _i$, which is true if and only if $|\lambda _i| > \gamma |g_i(x)|$.

In the first case C1, we have $\max \{ -|\lambda _i|^2, \gamma g_i(x) \lambda _i \}=-|\lambda _i|^2$. Since (14b) and (55) imply $|\lambda _i^+|\le |\lambda _i|$, and hence $|\lambda _i^+-\lambda _i|\le 2|\lambda _i|$, we can write

$$\begin{aligned} -2\gamma (g_i(x)-g_i(x^\star ))\lambda _i&+ \gamma \beta (g_i(x)-g_i(x^\star )) (\lambda _i^+-\lambda _i) \\&\quad \le 2(1+\beta )\gamma |g_i(x)-g_i(x^\star )| |\lambda _i|\\&\quad \le 2(1+\beta )k_1 \gamma |\tilde{x}||\lambda _i| \le (1+\beta )k_1\gamma \left( \delta _2 |\tilde{x}|^2 + \frac{1}{\delta _2} |\lambda _i|^2\right) , \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$, in which $\delta _2$ is defined in (16). The above inequality and $\gamma <{{\bar{\gamma }}}_{9}$ (see (19d)) lead to

$$\begin{aligned} C1\implies \Delta _i&\le \left( \gamma ^2\alpha _{11} + \gamma \frac{(1+\beta )k_1}{\delta _2} -1\right) |\lambda _i|^2 +\gamma (1+\beta )k_1 \delta _2 |\tilde{x}|^2 \nonumber \\&\le -\frac{1}{2} |\lambda _i|^2 + \gamma (1+\beta )k_1 \delta _2 |\tilde{x}|^2. \end{aligned}$$

(59)

In the second case C2, we have

$$\begin{aligned}\max \{ -|\lambda _i|^2, \gamma g_i(x) \lambda _i \}=\gamma g_i(x) \lambda _i = \gamma g_i(x^\star )\lambda _i + \gamma (g_i(x) -g_i(x^\star )) \lambda _i. \end{aligned}$$

Moreover, in view of (11), (17), and (18), $g_i(x^\star ) = -|g_i(x^\star )| \le -h$ for all $i\in \text {I}$. Hence, using again $|\lambda _i^+-\lambda _i|\le 2|\lambda _i|$, and $|\lambda _i|\le K$, and since $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }\implies |\tilde{x}|\le \varepsilon$, we obtain

$$\begin{aligned} \Delta _i&= \gamma g_i(x^\star )\lambda _i - \gamma (g_i(x) -g_i(x^\star )) \lambda _i + \gamma \beta (g_i(x) -g_i(x^\star )) (\lambda _i^+-\lambda _i) + \gamma ^2\alpha _{11} |\lambda _i|^2\\&\le \gamma \big ( \gamma \alpha _{11} K + (1+2\beta )|g_i(x)-g_i(x^\star )|-h \big )|\lambda _i| \\&\le \gamma \big ( \gamma \alpha _{11} K + (1+2\beta )k_1\varepsilon -h \big )|\lambda _i| \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$. Using $\gamma <{{\bar{\gamma }}}_{10}$ (see (19d), (17) and (18)) thus yields

$$\begin{aligned} C2\implies \Delta _i \le -\gamma \frac{h}{2} |\lambda _i| \le -\gamma \frac{h}{2} |\lambda _i|+ \gamma (1+\beta )k_1 \delta _2 |\tilde{x}|^2 \end{aligned}$$

(60)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

By joining (59) and (60), we thus obtain

$$\begin{aligned} \forall (x,\lambda )\in \Omega _\rho ^{\le \varepsilon },\quad \Delta _i \le \frac{1}{2}\max \left\{ - |\lambda _i|^2,\ -\gamma h |\lambda _i| \right\} + \gamma (1+\beta )k_1 \delta _2 |\tilde{x}|^2, \end{aligned}$$

for all $i\in \text {I}$. Finally, including the latter inequality in (58), and using $\gamma \le {{\bar{\gamma }}}_{11}$ (see (19e)) and the definition of $\delta _1$ and $\delta _2$ (see (16)), we obtain

$$\begin{aligned} V(x^+,\lambda ^+)&\le V(x,\lambda ) -\frac{1}{2}\sum _{i=r_a+1}^{r} \min \left\{ |\lambda _i|^2 ,\ \gamma h|\lambda _i| \right\} \nonumber \\ {}&\quad + \Big ( \gamma (r-r_a)(1+\beta )k_1 \delta _2 + \gamma ^2 \alpha _7+ \gamma ^4 \alpha _8 -\gamma c_0\Big )|\tilde{x}|^2 \nonumber \\&\quad + \left( \gamma ^2 \left( \delta _1\alpha _9 - \frac{k_2^2}{2} \right) + \gamma ^4 \alpha _{10}\right) |\tilde{\lambda }_\text {A}|^2 \nonumber \\&= V(x,\lambda ) -\frac{1}{2}\sum _{i=r_a+1}^{r} \min \left\{ |\lambda _i|^2 ,\ \gamma h|\lambda _i| \right\} \nonumber \\&\quad + \gamma \left( \gamma \alpha _7+ \gamma ^3 \alpha _8 - \frac{c_0}{2} \right) |\tilde{x}|^2 + \gamma ^2\left( \gamma ^2 \alpha _{10} - \frac{3k_2^2}{8} \right) |\tilde{\lambda }_\text {A}|^2 \nonumber \\&\le V(x,\lambda ) -\frac{1}{2}\sum _{i=r_a+1}^{r} \min \left\{ |\lambda _i|^2 ,\ \gamma h|\lambda _i| \right\} - \frac{1}{4} \gamma c_0 |\tilde{x}|^2 - \frac{1}{4} \gamma ^2 k_2^2 |\tilde{\lambda }_\text {A}|^2 \end{aligned}$$

(61)

for all $(x,\lambda )\in \Omega _\rho ^{\le \varepsilon }$.

4.6 Equiboundedness and convergence

The lemma below summarizes the results of the previous subsections.

Lemma 8

Suppose that Assumptions 1 and 2 hold, and let $\gamma$ satisfy (20). Then

$$\begin{aligned}&V(x,\lambda )^+ - V(x,\lambda ) \\&\quad \le -\min \left\{ \gamma c_0\varepsilon ^2,\ \frac{1}{2}\sum _{i=r_a+1}^{r} \min \left\{ |\lambda _i|^2 ,\ \gamma h|\lambda _i| \right\} + \frac{1}{4} \gamma c_0 |\tilde{x}|^2 + \frac{1}{4} \gamma ^2 k_2^2 |\tilde{\lambda }_\text {A}|^2 \right\} , \end{aligned}$$

for all $(x,\lambda )\in \Omega _\rho$.

Proof

The proof directly follows from (34) and (61) since $\Omega _\rho = \Omega _\rho ^{>\varepsilon }\cup \Omega _\rho ^{\le \varepsilon }$.$\square$

Lemma 8 ultimately enables us to conclude that the following implications hold for all $t\ge 0$

$$\begin{aligned} (x^t, \lambda ^t) \in \Omega _\rho \implies V(x^{t+1},\lambda ^{t+1}) \le V(x^{t},\lambda ^{t}) {\le }\rho \implies (x^{t+1}, \lambda ^{t+1}) \in \Omega _\rho . \end{aligned}$$

Since, in view of (7) and Lemma 7, we have

$$\begin{aligned} (x_0,\lambda _0) \in \Xi _0 \subseteq {\overline{{\mathbb {B}}}}_{K_0}(x^\star ,\lambda ^\star ) \subseteq \Omega _\rho , \end{aligned}$$

then we claim by induction on t that every solution of (5) originating in $\Xi _0$ satisfies

$$\begin{aligned} \forall t\in {\mathbb {N}},\qquad (x^t,\lambda ^t)\in \Omega _\rho . \end{aligned}$$

(62)

Relation (62) implies that all the trajectories of (5) originating in $\Xi _0$ are equibounded. Moreover, (62), Lemma 6, and Lemma 8 imply that every solution of (5) originating in $\Xi _0$ satisfies $V(x^t,\lambda ^t)\rightarrow 0$ and $(x^t,\lambda ^t)\rightarrow (x^\star ,\lambda ^\star )$.

4.7 Convergence rate and exponential bound

We now conclude the proof of the theorem by establishing the claimed exponential bound. As a first step, we prove the following lemma showing that, for every $\eta >0$, all solutions of (5) originating in $\Xi _0$ enter into an invariant set where $V(x,\lambda )\le \frac{1}{2}\min \left\{ \eta ^2,\varepsilon ^2\right\}$ in the same common time.

Lemma 9

Suppose that Assumptions 1 and 2 hold, and let $\gamma$ satisfy (20). For every $\eta >0$, let

$$\begin{aligned} T{:}{=}\frac{6(2\rho - \min \{\eta ^2,\varepsilon ^2\} )}{\min \left\{ 2,\,\gamma c_0,\, \gamma ^2 k_2^2\right\} \min \left\{ \eta ^2,\varepsilon ^2\right\} }. \end{aligned}$$

(63)

Then, every solution of (5) originating in $\Xi _0$ satisfies

$$\begin{aligned} \forall t\ge T,\qquad V(x^t,\lambda ^t)\le \frac{1}{2}\min \left\{ \eta ^2,\varepsilon ^2\right\} . \end{aligned}$$

Proof

Fix $\eta >0$ arbitrarily and define

$$\begin{aligned} \upsilon {:}{=}\frac{1}{2}\min \left\{ \eta ^2,\varepsilon ^2\right\} . \end{aligned}$$

Pick a solution $(x,\lambda )$ of (5) originating in $\Xi _0$, and let $\tau \in {\mathbb {N}}$ be such that $V(x^t,\lambda ^t)>\upsilon$ for all $t\in {\mathbb {N}}_{<\tau }$ and $V(x_\tau ,\lambda _\tau )\le \upsilon$. The existence of such $\tau$ is implied by the convergence of $(x,\lambda )$ to $(x^\star ,\lambda ^\star )$ established in previous Sect. 4.6. In view of (62), Lemma 8 implies $V(x^t,\lambda ^t)\le \upsilon$ for all $t\ge \tau$. Therefore, to prove the lemma, it suffices to show that $\tau \le T$, with T defined in (63). By contradiction, suppose $\tau >T$. Then, $V(x^t,\lambda ^t)>\upsilon$ for all $t\in {\mathbb {N}}_{\le T}$.

For each $t\in {\mathbb {N}}$, let $\text {I}_1^t\subseteq \text {I}$ be the set of $i\in \text {I}$ such that $\lambda _i^t \le \gamma h$. Let $I_2^t = \text {I}^t {\setminus } \text {I}_1^t$.

Then, we obtain (we omit the time dependency for readability)

$$\begin{aligned} \sum _{i=r_a+1}^{r} \min \left\{ |\lambda _i|^2 ,\ \gamma h|\lambda _i| \right\} = |\lambda _{\text {I}_{1}}|^2 + \gamma h \sum _{i\in \text {I}_2} |\lambda _i|. \end{aligned}$$

Moreover, Lemma 8 and Lemma 6 (see (26)) imply

$$\begin{aligned}&V(x,\lambda )^+ - V(x,\lambda ) \nonumber \\&\quad \le \max \left\{ -\gamma c_0\varepsilon ^2,\ -\frac{1}{2}\gamma h\sum _{i\in \text {I}_2} |\lambda _i| - \frac{1}{4}\min \{ 2, \gamma c_0, \gamma ^2 k_2^2\} \left( |\tilde{x}|^2 + |\tilde{\lambda }_{\text {A}}|^2 + |\lambda _{\text {I}_1}|^2\right) \right\} \nonumber \\&\quad = \max \left\{ -\gamma c_0\varepsilon ^2,\ -\frac{1}{2}\gamma h\sum _{i\in \text {I}_2} |\lambda _i| - \frac{1}{4}\min \{ 2, \gamma c_0, \gamma ^2 k_2^2\} \left( |(\tilde{x},\tilde{\lambda })|^2- |\lambda _{\text {I}_2}|^2\right) \right\} . \end{aligned}$$

(64)

Since $(x,\lambda )\in \Omega _\rho$ implies $|\lambda _{i}|\le K$ for all $i\in \text {I}$, then $\gamma <{{\bar{\gamma }}}_{12}$ (see (19e)) yields

$$\begin{aligned} \frac{1}{4}\min \{2,\,\gamma c_0,\, \gamma ^2 k_2^2\}|\lambda _{\text {I}_2}|^2 - \frac{1}{2}\sum _{i\in \text {I}_2} \gamma h |\lambda _i|&\le \sum _{i\in \text {I}_2}\left( \frac{\gamma ^2 k_2^2}{4} |\lambda _{i}|^2 - \frac{\gamma h}{2} |\lambda _i| \right) \nonumber \\&\le \frac{\gamma }{2}\sum _{i\in \text {I}_2}\left( \gamma \frac{k_2^2K}{2}- h \right) |\lambda _i| \le 0. \end{aligned}$$

Hence, from (64) we obtain

$$\begin{aligned}&V(x,\lambda )^+ - V(x,\lambda ) \le \max \left\{ -\gamma c_0\varepsilon ^2,\ - \frac{1}{6}\min \{ 2, \gamma c_0, \gamma ^2 k_2^2\} V(x,\lambda ) \right\} . \end{aligned}$$

Using $t\le T\implies V(x^t,\lambda ^t)>\upsilon$, we then obtain

$$\begin{aligned}&V(x^{t+1},\lambda ^{t+1}) \\&\quad \le V(x^t,\lambda ^t) - \min \left\{ \gamma c_0\varepsilon ^2, \frac{1}{12}\min \{ 2, \gamma c_0, \gamma ^2 k_2^2\}\min \{\eta ^2,\varepsilon ^2\} \right\} \\&\quad = V(x^t,\lambda ^t) - \min \left\{ \gamma c_0\varepsilon ^2, \frac{1}{12}\gamma c_0 \varepsilon ^2, \frac{1}{12}\gamma c_0\eta ^2, \frac{1}{12}\min \{ 2, \gamma ^2 k_2^2\}\min \{\eta ^2,\varepsilon ^2\} \right\} \\&\quad = V(x^t,\lambda ^t) - \min \left\{ \frac{1}{12}\gamma c_0 \varepsilon ^2, \frac{1}{12}\gamma c_0\eta ^2, \frac{1}{12}\min \{ 2, \gamma ^2 k_2^2\}\min \{\eta ^2,\varepsilon ^2\} \right\} \\&\quad =V - \frac{1}{12}\min \{ 2, \gamma c_0, \gamma ^2 k_2^2\}\min \{\eta ^2,\varepsilon ^2\} . \end{aligned}$$

Namely,

$$\begin{aligned} \forall t\in {\mathbb {N}}_{\le T},\quad V(x^{t+1},\lambda ^{t+1}) \le V(x^t,\lambda ^t) - \chi (\gamma ) \end{aligned}$$

in which

$$\begin{aligned}&\chi (\gamma ) {:}{=}\frac{1}{6} \min \left\{ 2,\,\gamma c_0,\, \gamma ^2 k_2^2\right\} ,\\ {}&\upsilon = \frac{1}{12} \min \left\{ 2,\,\gamma c_0,\, \gamma ^2 k_2^2\right\} \min \left\{ \eta ^2,\varepsilon ^2\right\} . \end{aligned}$$

As $V(x^0,\lambda ^0)\le \rho$ (by Lemma 7) we thus obtain

$$\begin{aligned} V(x^{T},\lambda ^{T}) \le \rho - \chi (\gamma ) T= \upsilon , \end{aligned}$$

which contradicts $V(x^{T},\lambda ^{T})>\upsilon$, so that the proof follows. $\square$

The following lemma, instead, provides conditions for local exponential convergence.

Lemma 10

Suppose that Assumptions 1 and 2 hold, and let $\gamma$ satisfy (20). Let $\mu \in [0,1)$ and $a\in (0,\rho )$ be such that

$$\begin{aligned} V(x,\lambda )\le a\implies V(x^+,\lambda ^+) \le \mu ^2V(x,\lambda ). \end{aligned}$$

Finally, let $T\in {\mathbb {N}}$ be such that every solution of (5) originating in $\Xi _0$ satisfies $V(x^T,\lambda ^T)\le a$. Then, every solution of (5) originating in $\Xi _0$ also satisfies

$$\begin{aligned} \forall t\in {\mathbb {N}},\quad |(\tilde{x}^t,\tilde{\lambda }^t)|\le \sqrt{3} \mu ^{t-T} |(\tilde{x}^0,\tilde{\lambda }^0)|. \end{aligned}$$

Proof

Pick a solution of (5) originating in $\Xi _0$. Lemma 8 and (62) and imply $V(x^T,\lambda ^T)\le V(x^0,\lambda ^0)$. Moreover, as $a<\rho$, Lemma 8 implies $V(x^t,\lambda ^t)\le V(x^T,\lambda ^T)\le a$ for all $t\ge T$.

Hence, in view of Lemma 6, we obtain

$$\begin{aligned}&\forall t\ge T,\quad V(x^t,\lambda ^t)\le \mu ^{2(t-T)} V(x^T,\lambda ^T) \le \mu ^{2(t-T)} V(x^0,\lambda ^0) \le \mu ^{2(t-T)} \frac{3}{2} |(\tilde{x}^0,\tilde{\lambda }^0)|^2 \\&\implies \forall t\ge T,\quad |(\tilde{x}^t,\tilde{\lambda }^t)|^2 \le 2 V(x^t,\lambda ^t) \le 3 \mu ^{2(t-T)} |(\tilde{x}^0,\tilde{\lambda }^0)|^2 . \end{aligned}$$

Instead, for $t\le T$, one has

$$\begin{aligned} |(\tilde{x}^t,\tilde{\lambda }^t)|^2\le 2V(x^t,\lambda ^t)\le 2V(x^0,\lambda ^0)\le 3V(x^0,\lambda ^0) \le 3 \mu ^{2(t-T)}V(x^0,\lambda ^0), \end{aligned}$$

where we used the fact that, since $\mu \in [0,1)$, then $\mu ^{2(t-T)}\ge 1$ for all $t\le T$.$\square$

With Lemmas 9 and 10 at hand, we can now prove the claimed exponential bound. First, assume that

$$\begin{aligned} V(x,\lambda )\le a{:}{=}\frac{1}{2}\min \left\{ \varepsilon ^2,\,\gamma ^2h^2,\,2\rho \right\} . \end{aligned}$$

(65)

Using $|\tilde{x}|^2\le |(\tilde{x},\tilde{\lambda })|^2 \le 2 V(x,\lambda )$ and $|\lambda _i|^2\le |(\tilde{x},\tilde{\lambda })|^2 \le 2 V(x,\lambda )$ for all $i\in \text {I}$ (in view of Lemma 6), we get that (65) implies

$$\begin{aligned} (x,\lambda )&\in \Omega _\rho ^{\le \varepsilon },\\ \forall i\in \text {I},\ \ |\lambda _i|&\le \gamma h , \end{aligned}$$

and, hence,

$$\begin{aligned} \forall i\in \text {I},\quad \min \big \{|\lambda _i|^2,\ \gamma h |\lambda _i|\big \} = |\lambda _i|^2. \end{aligned}$$

Then, we can manipulate (61) exploiting Lemma 6 to assert that, if (65) holds, then

$$\begin{aligned} V(x^+,\lambda ^+)&\le V(x,\lambda ) -\frac{1}{2} |\lambda _\text {I}|^2 - \frac{1}{4} \gamma c_0 |\tilde{x}|^2 - \frac{1}{4} \gamma ^2 k_2^2 |\tilde{\lambda }_\text {A}|^2 \nonumber \\&\le V(x,\lambda ) - \frac{1}{4}\min \left\{ 2,\,\gamma c_0,\,\gamma ^2 k_2^2\right\} \left( |\tilde{x}|^2+|\tilde{\lambda }|^2\right) \nonumber \\&\le \left( 1 - \frac{1}{6}\min \left\{ 2,\,\gamma c_0,\,\gamma ^2 k_2^2\right\} \right) V(x,\lambda ) \nonumber \\&= \mu ^2 V(x,\lambda ) \end{aligned}$$

(66)

with

$$\begin{aligned} \mu {:}{=}\sqrt{1 - \frac{1}{6}\min \left\{ 2,\,\gamma c_0,\,\gamma ^2 k_2^2\right\} } \ \in \ [0,1). \end{aligned}$$

Thus, we have established the implication

$$\begin{aligned} V(x,\lambda )\le a\implies V(x^+,\lambda ^+) \le \mu ^2V(x,\lambda ) \end{aligned}$$

(67)

$a\in (0,\rho )$ defined in (65).

Next, we apply Lemma 9 with

$$\begin{aligned} \eta {:}{=}\gamma h, \end{aligned}$$

obtaining that every solution of (5) originating in $\Xi _0$ satisfies

$$\begin{aligned} \forall t\ge T,\quad V(x^t,\lambda ^t)\le a \end{aligned}$$

(68)

in which T has the expression (63) with $\eta =\gamma h$.

The claim of the theorem finally follows from Lemma 10 in view of (65), (66), and (68).

5 Conclusions

This article considered the long-standing open problem of nonlocal asymptotic stability of the popular discrete-time primal-dual algorithm (1) for convex, constrained optimization. In particular, under due convexity and regularity assumptions, it is proved that an optimal equilibrium exists, it is unique, and it is semiglobally asymptotically stable. Namely, for every compact set of initial conditions, there exists a sufficiently small stepsize, such that the sequences generated by the algorithm converge to the optimal solution of the optimization problem and to the optimal Lagrange multipliers. Moreover, convergence is exponential, and the optimal point is Lyapunov stable. As shown in Sect. 1.2, global asymptotic stability cannot be established for the considered algorithm, so as semiglobal guarantees are the best achievable in the general case.

The key idea inspiring the stability analysis pursued in the article was to look at Algorithm (1) as a discrete-time dynamical system sharing many similarities with a nonlinear oscillator. This motivated the usage of a non-trivial Lyapunov function with a suitably-defined cross-term, unlike Uzawa’s previous attempt in [29].

Finally, it is worth remarking that the impossibility of global convergence of the algorithm complicates the development of robustness corollaries, which cannot be global in the size of the uncertainty. As a consequence, such shortfall poses new challenges in the design of distributed algorithms based on (1) and targeting, e.g., consensus optimization problems over networks [20,21,22, 24]. Future research will mainly focus on this latter extension.

A Proof of Lemma 1

First, notice that, since by 1-B each $g_i$ is continuous, then $G_i{:}{=}\{x\in {\mathbb {R}}^n\,:\,g_i(x)\le 0\}$ is closed for all $i=1,\dots ,r$. Hence, $G{:}{=}\cap _{i=1,\dots ,r} G_i$ is closed. Condition 1-C further implies that G is nonempty.

Since, by 1-A, f is continuously differentiable and strongly convex, it has a global minimum $z\in {\mathbb {R}}^n$ at which $\nabla f(z)=0$, and there exists $m>0$ such that

$$\begin{aligned} \forall w,y\in {\mathbb {R}}^n,\qquad f(y)\ge f(w)+ \nabla f(w)(y-w)+ m |y-w|^2. \end{aligned}$$

(69)

In particular, (69) implies that, for all $c>f(z)$, $f^{-1}([f(z),c])$ is compact.

Let $(c_n)_{n\in {\mathbb {N}}}$ be an increasing sequence satisfying $c_n\rightarrow \infty$. Then, (69) implies that

$$\begin{aligned} \bigcup _{n\in {\mathbb {N}}} f^{-1}([f(z),c_{n}]) = {\mathbb {R}}^n. \end{aligned}$$

(70)

Indeed, pick $x\in {\mathbb {R}}^n$. Since $c_n\rightarrow \infty$, we can find $n_x\in {\mathbb {N}}$ sufficiently large so that $c_{n_x} \ge f(z) +|\nabla f(x)| |x-z|$. Then, (69) applied with $w=x$ and $y=z$ implies $f(x)\le c_{n_x}$, i.e., $x\in f^{-1}([f(z),c_{n_x}])$. In view of this, we can assume without loss of generality that, for all $n\in {\mathbb {N}}$, $\varnothing \ne A_n{:}{=}f^{-1}([f(z),c_n])\cap G$.

Since f is continuous and $A_n$ is compact and nonempty, for each $n\in {\mathbb {N}}$ there exists $x_n\in A_n$ satisfying $x_n = \mathop {\textrm{argmin}}\limits _{x\in A_n} f(x)$.

Since $c_{n+1}\ge c_n$, then $A_n\subseteq A_{n+1}$ and, hence, $f(x_{n+1})\le f(x_n)$. The sequence $(f(x_n))_{n\in {\mathbb {N}}}$ is therefore decreasing and lower-bounded by f(z). Hence, it has a limit $f_\infty {:}{=}\lim _{n\rightarrow \infty }f(x_n) = \inf _{n\in {\mathbb {N}}} f(x_n)$.

By using (69) with $(w,y)=(z,x_n)$, we obtain

$$\begin{aligned} \forall n\in {\mathbb {N}},\quad m|x_n-z|^2 \le f(x_n)-f(z) \le f(x_0)-f(z). \end{aligned}$$

Hence, the sequence $x_n$ has a converging subsequence that converges to some $x^\star \in {\mathbb {R}}^n$ satisfying $f(x^\star )=f_\infty$.

Since G is closed and $x_n\in A_n\subseteq G$ for all $n\in {\mathbb {N}}$, then $x^\star \in G$. Thus, $x^\star$ it is feasible for (2).

In view of (70), for every $x\in G$, there exists ${\bar{n}}\in {\mathbb {N}}$ such that $x\in A_{{\bar{n}}}$. Hence, $f(x)\ge f(x_{{\bar{n}}}) \ge f_\infty = f(x^\star )$. Since $x\in G$ was arbitrary, this shows that $x^\star$ is a minimum of f in G.

Finally, the uniqueness of $x^\star$ follows by the fact that f is strongly convex and G is a convex set since $g_i$ is convex for all $i=1,\dots ,r$. Indeed, suppose ${\bar{x}}\in G$ is another point satisfying $f({\bar{x}})=f(x^\star )=f_\infty$. Then, $|{\bar{x}}-x^\star |>0$ and, since G is convex, for every $t\in (0,1)$, $t{\bar{x}}+(1-t)x^\star \in G$. Since f is strongly convex then this implies that, for some $m>0$,

$$\begin{aligned} f(t{\bar{x}}+(1-t)x^\star ) \le \underbrace{tf({\bar{x}}) +(1-t) f(x^\star )}_{=f_\infty } - mt (1-t)|{\bar{x}}-x^\star |^2 < f_\infty , \end{aligned}$$

which violates the fact shown earlier that $f(x)\ge f_\infty$ for all $x\in G$.